Теория столкновения

Принцип химии

Скорость реакции имеет тенденцию к увеличению с концентрацией феномена, объясняемого теорией столкновений

Теория столкновений — это принцип химии, используемый для прогнозирования скоростей химических реакций . Он гласит, что когда подходящие частицы реагента сталкиваются друг с другом с правильной ориентацией, только определенное количество столкновений приводит к ощутимому или заметному изменению; эти успешные изменения называются успешными столкновениями. Успешные столкновения должны иметь достаточно энергии, также известной как энергия активации , в момент удара, чтобы разорвать уже существующие связи и образовать все новые связи. Это приводит к продуктам реакции. Энергия активации часто предсказывается с помощью теории переходного состояния . Увеличение концентрации реагента приводит к большему количеству столкновений и, следовательно, к большему количеству успешных столкновений. Повышение температуры увеличивает среднюю кинетическую энергию молекул в растворе, увеличивая число столкновений, которые имеют достаточно энергии. Теория столкновений была предложена независимо Максом Траутцем в 1916 году ^[1] и Уильямом Льюисом в 1918 году. ^{[2] [3]}

Когда в столкновении между молекулами реагентов участвует катализатор, для осуществления химического изменения требуется меньше энергии, и, следовательно, больше столкновений имеют достаточно энергии для осуществления реакции. Скорость реакции, таким образом, увеличивается.

Теория столкновений тесно связана с химической кинетикой .

Теория столкновений изначально была разработана для системы газовых реакций без разбавления. Но большинство реакций включают растворы, например, газовые реакции в несущем инертном газе и почти все реакции в растворах. Частота столкновений молекул растворенного вещества в этих растворах теперь контролируется диффузией или броуновским движением отдельных молекул. Поток диффузионных молекул следует законам диффузии Фика . Для частиц в растворе примером модели для расчета частоты столкновений и связанной с ними скорости коагуляции является уравнение коагуляции Смолуховского, предложенное Марианом Смолуховским в основополагающей публикации 1916 года. ^[4] В этой модели поток Фика на бесконечном временном пределе используется для имитации скорости частиц теории столкновений. Цзисинь Чен предложил конечное временное решение для диффузионного потока в 2022 году, которое существенно изменяет расчетную частоту столкновений двух частиц в растворе. ^[5]

Уравнения скорости

Скорость бимолекулярной газофазной реакции A + B → продукт, предсказанная теорией столкновений, равна ^[6]

${\displaystyle r(T)=kn_{\text{A}}n_{\text{B}}=Z\rho \exp \left({\frac {-E_{\text{a}}}{RT}}\right)}$

где:

• k — константа скорости в единицах (число молекул) ⁻¹ ⋅с ⁻¹ ⋅м ³ .
• n _A — плотность числа A в газе в единицах м ⁻³ .
• n _B — числовая плотность B в газе в единицах м ⁻³ . Например, для газовой смеси с концентрацией газа A 0,1 моль⋅л ⁻¹ и концентрацией B 0,2 моль⋅л ⁻¹ числовая плотность A равна 0,1×6,02×1023 ^÷ 10−3 ⁼ 6,02× ¹⁰²⁵ м ⁻³ , числовая плотность B равна 0,2×6,02×1023 ^÷ 10−3 ⁼ 1,2× ¹⁰²⁶ м ^−3.
• Z — частота столкновений в единицах м ⁻³ ⋅с ⁻¹ .
• ${\displaystyle \rho }$является стерическим фактором . ^[7]
• E _a — энергия активации реакции, в единицах Дж⋅моль ⁻¹ .
• T — температура в единицах К.
• R — газовая постоянная в единицах Дж моль ⁻¹ К ⁻¹ .

Единицу измерения r ( T ) можно преобразовать в моль⋅л ⁻¹ ⋅с ⁻¹ , разделив на (1000× N _A ), где N _A — постоянная Авогадро .

Для реакции между A и B частота столкновений , рассчитанная с помощью модели твердых сфер с единичным числом столкновений на м ³ в секунду, составляет:

${\displaystyle Z=n_{\text{A}}n_{\text{B}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}=10^{6}N_{A}^{2}{\text{[A][B]}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}}$

где:

• n _A — плотность числа A в газе в единицах м ⁻³ .
• n _B — числовая плотность B в газе в единицах м ⁻³ . Например, для газовой смеси с концентрацией газа A 0,1 моль⋅л ⁻¹ и концентрацией B 0,2 моль⋅л ⁻¹ числовая плотность A равна 0,1×6,02×1023 ^÷ 10−3 ⁼ 6,02× ¹⁰²⁵ м ⁻³ , числовая плотность B равна 0,2×6,02×1023 ^÷ 10−3 ⁼ 1,2× ¹⁰²⁶ м ⁻³ .
• σ _{AB —} сечение реакции (единица измерения м2 ⁾ , площадь, при которой две молекулы сталкиваются друг с другом, упрощенно равна , где r _A — радиус A, а r _B — радиус B в единицах измерения м. ${\displaystyle \sigma _{\text{AB}}=\pi (r_{\text{A}}+r_{\text{B}})^{2}}$
• k _B — единица постоянной Больцмана Дж⋅К ⁻¹ .
• T — абсолютная температура (единица К).
• μ _AB — приведенная масса реагентов A и B (единица измерения кг). ${\displaystyle \mu _{\text{AB}}={\frac {{m_{\text{A}}}{m_{\text{B}}}}{{m_{\text{A}}}+{m_{\text{B}}}}}}$
• N _A — постоянная Авогадро .
• [A] — молярная концентрация A в единицах моль⋅л ⁻¹ .
• [B] — молярная концентрация B в единицах моль⋅л ⁻¹ .
• Z можно преобразовать в число столкновений молей на литр в секунду, разделив на 1000 N _A.

_{Если все единицы ,} связанные с размерностью, перевести в дм, т.е. моль⋅дм ⁻³ для [A] и [B], дм2 ^для σAB , дм2 ⋅кг⋅с ^{−2 ⋅К} − ¹ для постоянной Больцмана , то

${\displaystyle Z=N_{\text{A}}\sigma _{\text{AB}}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{\text{AB}}}}}[{\text{A}}][{\text{B}}]=k[A][B]}$

единица моль⋅дм ⁻³ ⋅с ⁻¹ .

Количественные данные

Вывод

Рассмотрим бимолекулярную элементарную реакцию:

А + Б → В

В теории столкновений считается, что две частицы A и B столкнутся, если их ядра сблизятся больше, чем на определенное расстояние. Площадь вокруг молекулы A, в которой она может столкнуться с приближающейся молекулой B, называется поперечным сечением (σ _AB ) реакции и, упрощенно говоря, представляет собой площадь, соответствующую окружности, радиус которой ( ) является суммой радиусов обеих реагирующих молекул, которые предположительно являются сферическими. Таким образом, движущаяся молекула будет охватывать объем в секунду при своем движении, где - средняя скорость частицы. (Это представляет собой исключительно классическое представление о столкновении твердых шаров. Поскольку молекулы представляют собой квантово-механические многочастичные системы электронов и ядер, основанные на кулоновских и обменных взаимодействиях, они, как правило, не подчиняются вращательной симметрии и не имеют потенциала ящика. Поэтому, в более общем смысле, поперечное сечение определяется как вероятность реакции луча частиц A на поверхностную плотность мишеней B, что делает определение независимым от характера взаимодействия между A и B. Следовательно, радиус связан с масштабом длины их потенциала взаимодействия.) ${\displaystyle r_{AB}}$ ${\displaystyle \pi r_{AB}^{2}c_{A}}$ ${\displaystyle c_{A}}$ ${\displaystyle r_{AB}}$

Из кинетической теории известно, что молекула А имеет среднюю скорость (отличную от среднеквадратичной скорости) , где — постоянная Больцмана , а — масса молекулы. ${\displaystyle c_{A}={\sqrt {\frac {8k_{\text{B}}T}{\pi m_{A}}}}}$ ${\displaystyle k_{\text{B}}}$ ${\displaystyle m_{A}}$

Решение задачи двух тел гласит, что два различных движущихся тела можно рассматривать как одно тело, которое имеет приведенную массу обоих и движется со скоростью центра масс , поэтому в этой системе следует использовать вместо . Таким образом, для данной молекулы A она движется до столкновения с молекулой B, если все B зафиксированы без движения, где — среднее расстояние перемещения. Поскольку B также движется, относительную скорость можно вычислить, используя приведенную массу A и B. ${\displaystyle \mu _{AB}}$ ${\displaystyle m_{A}}$ ${\displaystyle t=l/c_{A}=1/(n_{B}\sigma _{AB}c_{A})}$ ${\displaystyle l}$

Следовательно, общая частота столкновений ^[8] всех молекул A со всеми молекулами B равна

${\displaystyle Z=n_{\text{A}}n_{\text{B}}\sigma _{AB}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}=10^{6}N_{A}^{2}[A][B]\sigma _{AB}{\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}=z[A][B],}$

Из распределения Максвелла-Больцмана можно вывести, что доля столкновений с энергией, большей энергии активации, равна . Таким образом, скорость бимолекулярной реакции для идеальных газов будет равна ${\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}$

${\displaystyle r=z\rho [A][B]\exp \left({\frac {-E_{\text{a}}}{RT}}\right),}$в единице числа молекулярных реакций с ⁻¹ ⋅м ⁻³ ,

где:

• Z — частота столкновений с единицей с ⁻¹ ⋅м ⁻³ . Z — это Z без [A][B].
• ${\displaystyle \rho }$- это стерический фактор , который будет подробно рассмотрен в следующем разделе,
• E _a — энергия активации (на моль) реакции в единицах Дж/моль,
• T — абсолютная температура в единицах К,
• R — газовая постоянная в единицах Дж/моль/К.
• [A] — молярная концентрация A в единицах моль/л,
• [B] — молярная концентрация B в единицах моль/л.

Произведение zρ эквивалентно предэкспоненциальному множителю уравнения Аррениуса .

Обоснованность теории и стерический фактор

После формулирования теории ее обоснованность необходимо проверить, то есть сравнить ее предсказания с результатами экспериментов.

Если сравнить форму выражения константы скорости с уравнением скорости элементарной бимолекулярной реакции, то можно заметить, что ${\displaystyle r=k(T)[A][B]}$

${\displaystyle k(T)=N_{A}\sigma _{AB}\rho {\sqrt {\frac {8k_{\text{B}}T}{\pi \mu _{AB}}}}\exp \left({\frac {-E_{\text{a}}}{RT}}\right)}$

единица М ⁻¹ ⋅с ⁻¹ (= дм ³ ⋅моль ⁻¹ ⋅с ⁻¹ ), со всеми единицами размерности дм, включая k _B .

Это выражение похоже на уравнение Аррениуса и дает первое теоретическое объяснение уравнения Аррениуса на молекулярной основе. Слабая температурная зависимость предэкспоненциального множителя настолько мала по сравнению с экспоненциальным множителем, что ее невозможно измерить экспериментально, то есть «невозможно установить на основе температурных исследований константы скорости, является ли предсказанное значение T ^⁠1/2⁠ зависимость предэкспоненциального множителя наблюдается экспериментально». ^[9]

Стерический фактор

Если значения предсказанных констант скорости сравниваются со значениями известных констант скорости, то можно заметить, что теория столкновений не может правильно оценить константы, и чем сложнее молекулы, тем больше она не может. Причина этого в том, что частицы предполагались сферическими и способными реагировать во всех направлениях, что неверно, так как ориентация столкновений не всегда соответствует реакции. Например, в реакции гидрирования этилена молекула H2 должна приблизиться к зоне связи между атомами, и только несколько из всех возможных столкновений удовлетворяют _этому требованию.

Чтобы решить эту проблему, необходимо ввести новое понятие: стерический фактор ρ . Он определяется как отношение экспериментального значения к предсказанному (или отношение частотного фактора к частоте столкновений):

${\displaystyle \rho ={\frac {A_{\text{observed}}}{Z_{\text{calculated}}}},}$

и чаще всего он меньше единицы. ^[7]

Обычно, чем сложнее молекулы реагентов, тем ниже стерический фактор. Тем не менее, некоторые реакции демонстрируют стерические факторы больше единицы: реакции гарпуна , в которых участвуют атомы, обменивающиеся электронами , производя ионы . Отклонение от единицы может иметь разные причины: молекулы не сферические, поэтому возможны разные геометрии; не вся кинетическая энергия доставляется в нужное место; присутствие растворителя (при применении к растворам) и т. д.

Теория столкновений может быть применена к реакциям в растворе; в этом случае клетка растворителя оказывает влияние на молекулы реагентов, и несколько столкновений могут происходить в одной столкновении, что приводит к тому, что предсказанные предэкспоненциальные множители оказываются слишком большими. Значения ρ больше единицы можно отнести к благоприятным энтропийным вкладам.

Альтернативные модели столкновений для разбавленных растворов

Столкновения в разбавленном газе или жидком растворе регулируются диффузией вместо прямых столкновений, которые можно рассчитать с помощью законов диффузии Фика . Теоретические модели для расчета частоты столкновений в растворах были предложены Марианом Смолуховским в основополагающей публикации 1916 года при бесконечном пределе времени ^[4] и Цзисинем Ченом в 2022 году при приближении конечного времени ^[5] . Схема сравнения уравнений скорости в чистом газе и растворе показана на правом рисунке.

Схема, сравнивающая прямое столкновение и диффузионное столкновение, с соответствующими уравнениями скорости.

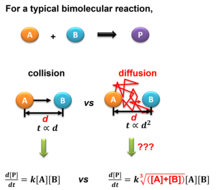
Для разбавленного раствора в газовой или жидкой фазе уравнение столкновения, разработанное для чистого газа, не подходит, когда диффузия берет под контроль частоту столкновений, т. е. прямое столкновение между двумя молекулами больше не доминирует. Для любой данной молекулы A она должна столкнуться со множеством молекул растворителя, скажем, молекулой C, прежде чем найти молекулу B для реакции. Таким образом, вероятность столкновения следует рассчитывать с использованием модели броуновского движения , которую можно аппроксимировать диффузионным потоком с использованием различных граничных условий, которые дают различные уравнения в модели Смолуховского и модели JChen.

Для диффузионного столкновения, в пределе бесконечного времени, когда молекулярный поток можно рассчитать с помощью законов диффузии Фика , в 1916 году Смолуховский вывел частоту столкновений между молекулами A и B в разбавленном растворе: ^[4]

${\displaystyle Z_{AB}=4\pi RD_{r}C_{A}C_{B}}$

где:

• ${\displaystyle Z_{AB}}$- частота столкновений, единица измерения: #столкновений/с в 1 м ³ раствора.
• ${\displaystyle R}$- радиус поперечного сечения столкновения, ед. м.
• ${\displaystyle D_{r}}$— относительная константа диффузии между А и В, единица измерения м ² /с, и . ${\displaystyle D_{r}=D_{A}+D_{B}}$
• ${\displaystyle C_{A}}$и — числовые концентрации молекул A и B в растворе соответственно, единица измерения #молекула/м ³ . ${\displaystyle C_{B}}$

или

${\displaystyle Z_{AB}=1000N_{A}*4\pi RD_{r}[A][B]=k[A][B]}$

где:

• ${\displaystyle Z_{AB}}$выражается в единицах мольных столкновений/с в 1 л раствора.
• ${\displaystyle N_{\text{A}}}$постоянная Авогадро .
• ${\displaystyle R}$- радиус поперечного сечения столкновения, ед. м.
• ${\displaystyle D_{r}}$относительная константа диффузии между А и В, единица измерения м ² /с.
• ${\displaystyle [A]}$и — молярные концентрации А и В соответственно, моль/л. ${\displaystyle [B]}$
• ${\displaystyle k}$константа скорости диффузионных столкновений, единица измерения л моль ⁻¹ с ⁻¹ .

С момента предложения модели Смолуховского в 1916 году ее подвергли множеству расширений и модификаций.

В 2022 году Чен рассуждает о том, что поскольку диффузионный поток развивается с течением времени, а расстояние между молекулами имеет конечное значение при данной концентрации, должно быть критическое время для прекращения эволюции потока, что даст значение, намного большее, чем бесконечное решение, предложенное Смолуховским. ^[5] Поэтому он предлагает использовать среднее время для двух молекул, чтобы поменяться местами в растворе, в качестве критического времени прекращения, т. е. время посещения первого соседа. Хотя альтернативным временем может быть среднее время свободного пробега или среднее время первого пассажира, оно переоценивает градиент концентрации между исходным местоположением первого пассажира и целью. Эта гипотеза дает фрактальное уравнение кинетической скорости реакции диффузионного столкновения в разбавленном растворе: ^[5]

${\displaystyle Z_{AB}=(1000N_{A})^{4/3}*8\pi ^{-1}A\beta D_{r}([A]+[B])^{1/3}[A][B]=k([A]+[B])^{1/3}[A][B]}$

где:

• ${\displaystyle Z_{AB}}$выражается в единицах мольных столкновений/с в 1 л раствора.
• ${\displaystyle N_{\text{A}}}$постоянная Авогадро .
• ${\displaystyle A}$- площадь поперечного сечения столкновения в единицах м ² .
• ${\displaystyle \beta }$— произведение безразмерных долей реакционной площади поверхности на А и В. — эффективная площадь поперечного сечения адсорбции. ${\displaystyle \beta A}$
• ${\displaystyle D_{r}}$— относительная константа диффузии между А и В, единица измерения м ² /с, и . ${\displaystyle D_{r}=D_{A}+D_{B}}$
• ${\displaystyle [A]}$и — молярные концентрации А и В соответственно, моль/л. ${\displaystyle [B]}$
• ${\displaystyle k}$константа скорости диффузионных столкновений, единица измерения л ^4/3 моль ^-4/3 с ⁻¹ .

Смотрите также

• Двумерный газ
• Уравнение скорости

Ссылки

1. Траутц, Макс. Das Gesetz der Reaktionsgeschwindigkeit und der Gleichgewichte в Гасене. Bestätigung der Additivität von Cv - 3/2 R. Neue Bestimmung der Integrationskonstanten und der Moleküldurchmesser, Zeitschrift für anorganische und allgemeine Chemie, том 96, выпуск 1, страницы 1–28, (1916).
2. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «теория столкновений». doi :10.1351/goldbook.C01170
3. Уильям Кадмор МакКаллах Льюис, XLI.—Исследования по катализу. Часть IX. Расчет в абсолютной мере констант скорости и констант равновесия в газообразных системах, J. Chem. Soc., Trans., 1918, 113, 471-492.
4. Смолуховский, Мариан (1916). «Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen». Физ. З. (на немецком языке). 17 : 557–571, ​​585–599. Бибкод : 1916ZPhy...17..557S.
5. Чен, Цзисинь (2022). «Почему порядок реакции бимолекулярной реакции должен быть 2,33, а не 2?». J. Phys. Chem. A. 126 : 9719–9725. doi :10.1021/acs.jpca.2c07500. PMC 9805503 . 
6. "6.1.6: Теория столкновения". 2 октября 2013 г.
7. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «стерический фактор». doi :10.1351/goldbook.S05998
8. IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «collision frequency». doi :10.1351/goldbook.C01166
9. Кеннет Коннорс, Химическая кинетика, 1990, VCH Publishers.
10. EA Moelwyn-Hughes, Кинетика реакций в растворе, 2-е изд., стр. 71.

Внешние ссылки

• Введение в теорию столкновений