
Электронные фильтры — это тип фильтра обработки сигнала в виде электрических цепей. В этой статье рассматриваются фильтры, состоящие из сосредоточенных электронных компонентов, в отличие от фильтров с распределенными элементами . То есть, использующие компоненты и соединения, которые при анализе можно считать существующими в одной точке. Эти компоненты могут быть в дискретных корпусах или быть частью интегральной схемы .
Электронные фильтры удаляют нежелательные частотные компоненты из подаваемого сигнала, усиливают нужные или и то, и другое. Они могут быть:
Наиболее распространенными типами электронных фильтров являются линейные фильтры , независимо от других аспектов их конструкции. Подробности их конструкции и анализа см. в статье о линейных фильтрах.
Самые старые формы электронных фильтров — это пассивные аналоговые линейные фильтры, построенные с использованием только резисторов и конденсаторов или резисторов и индуктивностей . Они известны как однополюсные фильтры RC и RL соответственно. Однако эти простые фильтры имеют очень ограниченное применение. Многополюсные LC-фильтры обеспечивают больший контроль над формой отклика, полосой пропускания и переходными полосами . Первым из этих фильтров был фильтр с постоянным k , изобретенный Джорджем Кэмпбеллом в 1910 году. Фильтр Кэмпбелла представлял собой лестничную сеть, основанную на теории линий передачи . Вместе с улучшенными фильтрами Отто Цобеля и других эти фильтры известны как фильтры параметров изображения . Большой шаг вперед был сделан Вильгельмом Кауэром , который основал область синтеза сетей во время Второй мировой войны . Теория Кауэра позволила конструировать фильтры, которые точно следовали некоторой предписанной частотной функции.
Пассивные реализации линейных фильтров основаны на комбинациях резисторов (R), индуктивностей (L) и конденсаторов (C). Эти типы известны как пассивные фильтры , поскольку они не зависят от внешнего источника питания и не содержат активных компонентов, таких как транзисторы .
Индукторы блокируют высокочастотные сигналы и проводят низкочастотные сигналы, в то время как конденсаторы делают обратное. Фильтр, в котором сигнал проходит через индуктор или в котором конденсатор обеспечивает путь к земле, представляет меньшее затухание низкочастотных сигналов, чем высокочастотных сигналов, и поэтому является фильтром нижних частот . Если сигнал проходит через конденсатор или имеет путь к земле через индуктор, то фильтр представляет меньшее затухание высокочастотных сигналов, чем низкочастотных сигналов, и поэтому является фильтром верхних частот . Резисторы сами по себе не обладают частотно-селективными свойствами, но добавляются к индукторам и конденсаторам для определения временных констант схемы и, следовательно, частот, на которые она реагирует.
Индукторы и конденсаторы являются реактивными элементами фильтра. Количество элементов определяет порядок фильтра. В этом контексте LC-настроенная цепь, используемая в полосовом или режекторном фильтре, считается одним элементом, даже если она состоит из двух компонентов.
На высоких частотах (выше примерно 100 мегагерц ) иногда индукторы состоят из отдельных петель или полос листового металла, а конденсаторы состоят из смежных полос металла. Эти индуктивные или емкостные куски металла называются заглушками .

Простейшие пассивные фильтры, RC и RL фильтры, включают в себя только один реактивный элемент, за исключением гибридного LC фильтра , который характеризуется индуктивностью и емкостью, объединенными в одном элементе. [1]
L-фильтр состоит из двух реактивных элементов, один из которых соединен последовательно, а другой — параллельно.
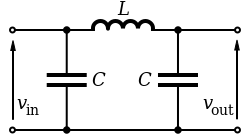

Трехэлементные фильтры могут иметь топологию «T» или «π», и в любой геометрии возможна характеристика нижних частот , верхних частот , полосовая или полосовая заграждающая характеристика. Компоненты могут быть выбраны симметричными или нет, в зависимости от требуемых частотных характеристик. Фильтр верхних частот T на иллюстрации имеет очень низкий импеданс на высоких частотах и очень высокий импеданс на низких частотах. Это означает, что его можно вставить в линию передачи, в результате чего высокие частоты будут пропущены, а низкие частоты будут отражены. Аналогично, для проиллюстрированного фильтра нижних частот π схема может быть подключена к линии передачи, пропуская низкие частоты и отражая высокие частоты. Используя m-производные секции фильтра с правильными оконечными импедансами, входной импеданс может быть достаточно постоянным в полосе пропускания. [2]
Фильтры с несколькими элементами обычно строятся как лестничная сеть . Их можно рассматривать как продолжение конструкций фильтров L,T и π. Больше элементов требуется, когда требуется улучшить некоторые параметры фильтра, такие как подавление полосы пропускания или наклон перехода от полосы пропускания к полосе задерживания.
Активные фильтры реализуются с использованием комбинации пассивных и активных (усиливающих) компонентов и требуют внешнего источника питания. Операционные усилители часто используются в конструкциях активных фильтров. Они могут иметь высокий коэффициент добротности и достигать резонанса без использования индукторов. Однако их верхний предел частоты ограничен полосой пропускания усилителей.
Существует множество технологий фильтрации, отличных от сосредоточенной компонентной электроники. К ним относятся цифровые фильтры , кристаллические фильтры , механические фильтры , фильтры на поверхностных акустических волнах (ПАВ), фильтры на основе тонкопленочных объемных акустических резонаторов (TFBAR, FBAR), гранатовые фильтры и атомные фильтры (используются в атомных часах ).
Передаточная функция фильтра — это отношение выходного сигнала к входному сигналу как функция комплексной частоты :
Передаточная функция всех линейных стационарных фильтров, построенных из сосредоточенных компонентов (в отличие от распределенных компонентов, таких как линии передачи), будет отношением двух полиномов в , т.е. рациональной функцией . Порядок передаточной функции будет наивысшей степенью , встречающейся либо в числителе, либо в знаменателе.
Электронные фильтры можно классифицировать по технологии, используемой для их реализации. Фильтры, использующие технологию пассивного фильтра и активную фильтрацию, можно далее классифицировать по конкретной топологии электронного фильтра, используемой для их реализации.
Любая заданная передаточная функция фильтра может быть реализована в любой топологии электронного фильтра .
Некоторые распространенные топологии схем:
Исторически линейный аналоговый дизайн фильтра развивался через три основных подхода. Самые старые конструкции представляют собой простые схемы, где основным критерием дизайна был коэффициент добротности схемы. Это отражало применение фильтрации в радиоприемниках, поскольку Q была мерой частотной избирательности настроечного контура. С 1920-х годов фильтры начали проектировать с точки зрения изображения , в основном руководствуясь требованиями телекоммуникаций. После Второй мировой войны доминирующей методологией стал сетевой синтез . Первоначально использовавшаяся высшая математика требовала публикации обширных таблиц значений полиномиальных коэффициентов, но современные компьютерные ресурсы сделали это ненужным. [3]
Фильтры низкого порядка могут быть разработаны путем прямого применения основных законов цепи, таких как законы Кирхгофа, для получения передаточной функции. Этот вид анализа обычно выполняется только для простых фильтров 1-го или 2-го порядка.

Этот подход анализирует секции фильтра с точки зрения фильтра, находящегося в бесконечной цепочке идентичных секций. Он имеет преимущества простоты подхода и возможности легкого расширения до более высоких порядков. Он имеет недостаток, заключающийся в том, что точность предсказанных ответов зависит от окончаний фильтра в импедансе изображения, что обычно не так. [4]


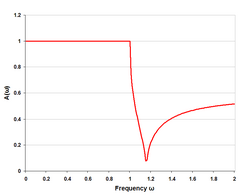

Подход к синтезу сети начинается с требуемой передаточной функции, а затем выражает ее как полиномиальное уравнение входного импеданса фильтра. Фактические значения элементов фильтра получаются путем разложения этого полинома в непрерывную дробь или частичную дробь. В отличие от метода изображения, нет необходимости в сетях согласования импеданса на окончаниях, поскольку эффекты согласующих резисторов включены в анализ с самого начала. [4]
Вот изображение, сравнивающее фильтры Баттерворта, Чебышева и эллиптические фильтры. Фильтры на этой иллюстрации — все фильтры нижних частот пятого порядка. Конкретная реализация — аналоговая или цифровая, пассивная или активная — не имеет значения; их выход будет одинаковым.

Как видно из изображения, эллиптические фильтры более резкие, чем все остальные, но они демонстрируют рябь по всей полосе пропускания.
{{cite book}}: CS1 maint: multiple names: authors list (link)Каталог типов пассивных фильтров и значений компонентов. Библия для практического проектирования электронных фильтров.