Эффект Джоуля-Томсона

Феномен изменения температуры неидеальных жидкостей при их прохождении через небольшие пространства

В термодинамике эффект Джоуля -Томсона (также известный как эффект Джоуля-Кельвина или эффект Кельвина-Джоуля ) описывает изменение температуры реального газа или жидкости (в отличие от идеального газа ) при его расширении; обычно вызванное потерей давления при прохождении потока через клапан или пористую пробку , при этом сохраняя его изолированным, так что не происходит обмена теплом с окружающей средой. ^{[1] [2] [3]} Эта процедура называется процессом дросселирования или процессом Джоуля-Томсона . ^[4] Эффект является чисто эффектом, обусловленным отклонением от идеальности, поскольку любой идеальный газ не имеет эффекта Джоуля-Томсона.

При комнатной температуре все газы, за исключением водорода , гелия и неона, охлаждаются при расширении в результате процесса Джоуля-Томсона при дросселировании через отверстие; эти три газа повышают температуру при продавливании через пористую пробку при комнатной температуре, но понижают температуру, когда уже находятся при более низких температурах. ^{[5] [6]} Большинство жидкостей, таких как гидравлические масла, будут нагреваться в результате процесса дросселирования Джоуля-Томсона. Температура, при которой эффект Джоуля-Томсона меняет знак, называется температурой инверсии .

Процесс дросселирования при охлаждении газа обычно используется в холодильных процессах , таких как ожижители в промышленном процессе разделения воздуха . ^{[7] [8]} В гидравлике эффект нагрева от дросселирования Джоуля-Томсона может быть использован для обнаружения внутренних протекающих клапанов, поскольку они будут производить тепло, которое можно обнаружить с помощью термопары или тепловизионной камеры . Дросселирование является принципиально необратимым процессом . Дросселирование из-за сопротивления потоку в линиях подачи, теплообменниках, регенераторах и других компонентах (тепловых) машин является источником потерь, которые ограничивают их производительность.

Поскольку это процесс постоянной энтальпии, его можно использовать для экспериментального измерения линий постоянной энтальпии (изоэнтальпий) на диаграмме газа. В сочетании с удельной теплоемкостью при постоянном давлении это позволяет полностью измерить термодинамический потенциал газа. ^[9] ${\displaystyle (p,T)}$ ${\displaystyle c_{P}=(\partial h/\partial T)_{P}}$

История

Эффект назван в честь Джеймса Прескотта Джоуля и Уильяма Томсона, 1-го барона Кельвина , которые открыли его в 1852 году. Он стал продолжением более ранней работы Джоуля о джоулевом расширении , в которой газ подвергается свободному расширению в вакууме , а температура не меняется, если газ идеален .

Описание

Адиабатическое (без теплообмена) расширение газа может осуществляться несколькими способами. Изменение температуры, испытываемое газом при расширении, зависит не только от начального и конечного давления, но и от способа, которым осуществляется расширение .

• Если процесс расширения обратим , то есть газ все время находится в термодинамическом равновесии , то это называется изоэнтропическим расширением. В этом сценарии газ совершает положительную работу во время расширения, а его температура понижается.
• С другой стороны, при свободном расширении газ не совершает работу и не поглощает тепло, поэтому внутренняя энергия сохраняется. При таком расширении температура идеального газа останется постоянной, но температура реального газа уменьшится, за исключением очень высокой температуры. ^[10]
• Метод расширения, обсуждаемый в этой статье, при котором газ или жидкость при давлении P ₁ перетекает в область с более низким давлением P ₂ без существенного изменения кинетической энергии, называется расширением Джоуля–Томсона. Расширение по своей сути необратимо. Во время этого расширения энтальпия остается неизменной (см. доказательство ниже). В отличие от свободного расширения, совершается работа, вызывающая изменение внутренней энергии. Увеличивается или уменьшается внутренняя энергия, определяется тем, совершается ли работа над жидкостью или ею; это определяется начальным и конечным состояниями расширения и свойствами жидкости.

Знак коэффициента Джоуля–Томсона для N ₂ . В области, ограниченной красной линией, расширение Джоуля–Томсона производит охлаждение ( ); за пределами этой области расширение производит нагревание. Кривая сосуществования газа и жидкости показана синей линией, заканчивающейся в критической точке (сплошной синий круг). Пунктирные линии разграничивают область, где N ₂ является сверхкритической жидкостью (где свойства плавно переходят от жидкоподобных к газоподобным). ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle \mu _{\mathrm {JT} }>0}$

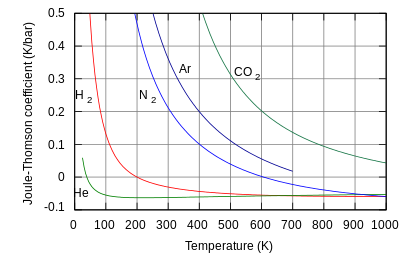
Изменение температуры, возникающее при расширении Джоуля-Томсона, количественно определяется коэффициентом Джоуля-Томсона, . Этот коэффициент может быть как положительным (соответствующим охлаждению), так и отрицательным (нагреванию); области, где каждый из них имеет место для молекулярного азота, N ₂ , показаны на рисунке. Обратите внимание, что большинство условий на рисунке соответствуют N ₂ как сверхкритической жидкости , где он имеет некоторые свойства газа и некоторые свойства жидкости, но не может быть на самом деле описан как таковой. Коэффициент отрицателен как при очень высоких, так и при очень низких температурах; при очень высоком давлении он отрицателен при всех температурах. Максимальная температура инверсии (621 К для N ₂ ^[11] ) достигается при приближении к нулевому давлению. Для газа N _{2 при низких давлениях отрицателен при высоких температурах и положителен при низких температурах. При температурах ниже} кривой сосуществования газа и жидкости N ₂ конденсируется, образуя жидкость, и коэффициент снова становится отрицательным. Таким образом, для газа N ₂ при температуре ниже 621 К можно использовать расширение Джоуля-Томсона для охлаждения газа до образования жидкого N ₂ . ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle \mu _{\mathrm {JT} }}$

Физический механизм

Существует два фактора, которые могут изменить температуру жидкости во время адиабатического расширения: изменение внутренней энергии или преобразование потенциальной и кинетической внутренней энергии. Температура является мерой тепловой кинетической энергии (энергии, связанной с молекулярным движением); поэтому изменение температуры указывает на изменение тепловой кинетической энергии. Внутренняя энергия представляет собой сумму тепловой кинетической энергии и тепловой потенциальной энергии. ^[12] Таким образом, даже если внутренняя энергия не изменяется, температура может измениться из-за преобразования кинетической и потенциальной энергии; это то, что происходит при свободном расширении и обычно приводит к снижению температуры по мере расширения жидкости. ^{[13] [14]} Если работа совершается над жидкостью или ею по мере ее расширения, то общая внутренняя энергия изменяется. Это то, что происходит при расширении Джоуля-Томсона и может привести к большему нагреву или охлаждению, чем наблюдается при свободном расширении.

В разложении Джоуля-Томсона энтальпия остается постоянной. Энтальпия, , определяется как ${\displaystyle H}$

${\displaystyle H=U+PV}$

где — внутренняя энергия, — давление, — объем. В условиях расширения Джоуля–Томсона изменение представляет собой работу, совершаемую жидкостью (см. доказательство ниже). Если увеличивается при постоянной, то должно уменьшаться в результате того, что жидкость совершает работу над своим окружением. Это приводит к снижению температуры и приводит к положительному коэффициенту Джоуля–Томсона. Наоборот, уменьшение означает, что работа совершается над жидкостью, а внутренняя энергия увеличивается. Если увеличение кинетической энергии превышает увеличение потенциальной энергии, произойдет увеличение температуры жидкости, а коэффициент Джоуля–Томсона будет отрицательным. ${\displaystyle U}$ ${\displaystyle P}$ ${\displaystyle V}$ ${\displaystyle PV}$ ${\displaystyle PV}$ ${\displaystyle H}$ ${\displaystyle U}$ ${\displaystyle PV}$

Для идеального газа не изменяется при расширении Джоуля-Томсона. ^[15] В результате внутренняя энергия не изменяется; поскольку также не изменяется тепловая потенциальная энергия, не может изменяться тепловая кинетическая энергия и, следовательно, не может изменяться температура. В реальных газах изменяется. ${\displaystyle PV}$ ${\displaystyle PV}$

Отношение значения к ожидаемому для идеального газа при той же температуре называется коэффициентом сжимаемости , . Для газа это обычно меньше единицы при низкой температуре и больше единицы при высокой температуре (см. обсуждение в коэффициенте сжимаемости ). При низком давлении значение всегда стремится к единице по мере расширения газа. ^[16] Таким образом, при низкой температуре и будет увеличиваться по мере расширения газа, что приведет к положительному коэффициенту Джоуля-Томсона. При высокой температуре и уменьшаться по мере расширения газа; если уменьшение достаточно велико, коэффициент Джоуля-Томсона будет отрицательным. ${\displaystyle PV}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle PV}$ ${\displaystyle Z}$ ${\displaystyle PV}$

Для жидкостей и для сверхкритических жидкостей под высоким давлением увеличивается с ростом давления. ^[16] Это происходит из-за того, что молекулы прижимаются друг к другу, так что объем едва может уменьшиться из-за более высокого давления. При таких условиях коэффициент Джоуля-Томсона отрицателен, как показано на рисунке выше. ${\displaystyle PV}$

Физический механизм, связанный с эффектом Джоуля-Томсона , тесно связан с механизмом ударной волны ^[17], хотя ударная волна отличается тем, что изменение объемной кинетической энергии газового потока не является незначительным.

Коэффициент Джоуля-Томсона (Кельвина)

Рис. 1 – Коэффициенты Джоуля–Томсона для различных газов при атмосферном давлении

Скорость изменения температуры относительно давления в процессе Джоуля-Томсона (то есть при постоянной энтальпии ) называется коэффициентом Джоуля-Томсона (Кельвина) . Этот коэффициент можно выразить через удельный объем газа , его теплоемкость при постоянном давлении и его коэффициент теплового расширения следующим образом: ^{[1] [3] [18]} ${\displaystyle T}$ ${\displaystyle P}$ ${\displaystyle H}$ ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle V}$ ${\displaystyle C_{\mathrm {p} }}$ ${\displaystyle \alpha }$

${\displaystyle \mu _{\mathrm {JT} }=\left({\partial T \over \partial P}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}(\alpha T-1)\,}$

Доказательство этого соотношения см. в разделе § Вывод коэффициента Джоуля-Томсона ниже. Значение обычно выражается в °C/ бар (единицы СИ: K / Па ) и зависит от типа газа, а также от температуры и давления газа до расширения. Его зависимость от давления обычно составляет всего несколько процентов для давлений до 100 бар. ${\displaystyle \mu _{\mathrm {JT} }}$

Все реальные газы имеют точку инверсии , в которой значение меняет знак. Температура этой точки, температура инверсии Джоуля–Томсона , зависит от давления газа до расширения. ${\displaystyle \mu _{\mathrm {JT} }}$

При расширении газа давление уменьшается, поэтому знак отрицателен по определению. Имея это в виду, следующая таблица объясняет, когда эффект Джоуля-Томсона охлаждает или нагревает реальный газ: ${\displaystyle \partial P}$

Гелий и водород — два газа, температура инверсии Джоуля–Томсона которых при давлении в одну атмосферу очень низкая (например, около 40 К, −233 °C для гелия). Таким образом, гелий и водород нагреваются при расширении с постоянной энтальпией при типичных комнатных температурах. С другой стороны, азот и кислород , два самых распространенных газа в воздухе, имеют температуру инверсии 621 К (348 °C) и 764 К (491 °C) соответственно: эти газы можно охладить от комнатной температуры с помощью эффекта Джоуля–Томсона. ^{[1] [11]}

Для идеального газа всегда равно нулю: идеальные газы не нагреваются и не охлаждаются при расширении при постоянной энтальпии. ${\displaystyle \mu _{\text{JT}}}$

Теоретические модели

Для газа Дитеричи соотношение между приведенным давлением и приведенной температурой инверсии равно . Воспроизведено с рис. 17 из ^[9] . ${\displaystyle {\tilde {p}}=(8-{\tilde {T}}_{I})e^{{\frac {5}{2}}-{\frac {4}{8-{\tilde {T}}_{I}}}}}$

Для газа Ван-дер-Ваальса коэффициент равен ^[19] с температурой инверсии . $${\displaystyle \mu _{\text{JT}}=-{\frac {V_{m}}{C_{p}}}{\frac {RTV_{m}^{2}b-2a(V_{m}-b)^{2}}{RTV_{m}^{3}-2a(V_{m}-b)^{2}}}.}$$ ${\displaystyle {\frac {2a}{bR}}\left(1-{\frac {b}{V_{m}}}\right)^{2}}$

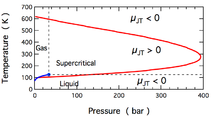
Для газа Дитеричи приведенная температура инверсии равна , а соотношение между приведенным давлением и приведенной температурой инверсии равно . Это изображено справа. Критическая точка попадает внутрь области, где газ охлаждается при расширении. Внешняя область — это область, где газ нагревается при расширении. ^[9] ${\displaystyle {\tilde {T}}_{I}=8-4/{\tilde {V}}_{m}}$ ${\displaystyle {\tilde {p}}=(8-{\tilde {T}}_{I})e^{{\frac {5}{2}}-{\frac {4}{8-{\tilde {T}}_{I}}}}}$

Приложения

На практике эффект Джоуля-Томсона достигается путем расширения газа через дроссельное устройство (обычно клапан ), которое должно быть очень хорошо изолировано, чтобы предотвратить любую передачу тепла газу или от него. Никакая внешняя работа не извлекается из газа во время расширения (газ не должен расширяться через турбину , например).

Охлаждение, производимое при расширении Джоуля-Томсона, делает его ценным инструментом в холодильной технике . ^{[8] [20]} Эффект применяется в технике Линде как стандартный процесс в нефтехимической промышленности , где охлаждающий эффект используется для сжижения газов , и во многих криогенных приложениях (например, для производства жидкого кислорода, азота и аргона ). Газ должен быть ниже своей температуры инверсии, чтобы быть сжиженным циклом Линде. По этой причине простые ожижители цикла Линде, начиная с температуры окружающей среды, не могут использоваться для сжижения гелия, водорода или неона . Сначала их необходимо охладить до их температур инверсии, которые составляют -233 °C (гелий), -71 °C (водород) и -42 °C (неон). ^[11]

Доказательство того, что удельная энтальпия остается постоянной

В термодинамике так называемые «удельные» величины являются величинами на единицу массы (кг) и обозначаются строчными буквами. Так, h , u и v являются удельной энтальпией , удельной внутренней энергией и удельным объемом (объемом на единицу массы или обратной плотностью) соответственно. В процессе Джоуля-Томсона удельная энтальпия h остается постоянной. ^[21] Чтобы доказать это, первым шагом является вычисление чистой работы, выполненной при перемещении массы m газа через пробку. Это количество газа имеет объем V ₁ = m v ₁ в области при давлении P ₁ (область 1) и объем V ₂ = m v ₂ в области при давлении P ₂ (область 2). Тогда в области 1 «работа потока», выполненная над количеством газа остальной частью газа, равна: W ₁ = m P ₁ v ₁ . В области 2 работа, совершаемая количеством газа над оставшимся газом, равна: W ₂ = m P ₂ v ₂ . Таким образом, полная работа, совершаемая над массой m газа, равна

${\displaystyle W=mP_{1}v_{1}-mP_{2}v_{2}.}$

Изменение внутренней энергии за вычетом полной работы, выполненной над количеством газа, согласно первому закону термодинамики , равно общему количеству тепла, переданному данному количеству газа.

${\displaystyle U-W=Q}$

В процессе Джоуля-Томсона газ изолирован, поэтому тепло не поглощается. Это означает, что

${\displaystyle {\begin{aligned}(mu_{2}-mu_{1})&-(mP_{1}v_{1}-mP_{2}v_{2})=0\\mu_{1}+mP_{1}v_{1}&=mu_{2}+mP_{2}v_{2}\\u_{1}+P_{1}v_{1}&=u_{2}+P_{2}v_{2}\end{aligned}}}$

где u ₁ и u ₂ обозначают удельные внутренние энергии газа в областях 1 и 2 соответственно. Используя определение удельной энтальпии h = u + Pv , из приведенного выше уравнения следует, что

${\displaystyle h_{1}=h_{2}}$

где h ₁ и h ₂ обозначают удельные энтальпии количества газа в областях 1 и 2 соответственно.

Дросселирование вТ-сдиаграмма

Рис. 2 – Диаграмма T - s азота. Красный купол представляет двухфазную область с низкоэнтропийной стороной (насыщенная жидкость) и высокоэнтропийной стороной (насыщенный газ). Черные кривые показывают соотношение T - s вдоль изобар. Давления указаны в барах. Синие кривые – изэнтальпии (кривые постоянной удельной энтальпии). Удельные энтальпии указаны в кДж/кг. Удельные точки a, b и т. д. рассматриваются в основном тексте.

Очень удобный способ получить количественное представление о процессе дросселирования — использовать диаграммы, такие как h - T диаграммы, h - P диаграммы и другие. Обычно используются так называемые T - s диаграммы. На рисунке 2 в качестве примера показана T - s диаграмма азота. ^[22] Различные точки обозначены следующим образом:

1. T = 300  К, p = 200 бар, s = 5,16  кДж/(кгК), h = 430  кДж/кг;
2. T = 270  К, p = 1 бар, s = 6,79  кДж/(кгК), h = 430  кДж/кг;
3. T = 133  К, p = 200 бар, s = 3,75  кДж/(кгК), h = 150  кДж/кг;
4. T = 77,2  К, p = 1 бар, s = 4,40  кДж/(кгК), h = 150  кДж/кг;
5. T = 77,2  К, p = 1 бар, s = 2,83  кДж/(кгК), h = 28  кДж/кг (насыщенная жидкость при 1 бар);
6. T = 77,2  К, p = 1 бар, s = 5,41  кДж/(кгК), h = 230  кДж/кг (насыщенный газ при 1 бар).

Как было показано ранее, дросселирование сохраняет h постоянным. Например, дросселирование от 200 бар и 300  К (точка a на рис. 2) следует изоэнтальпии (линии постоянной удельной энтальпии) 430  кДж/кг. При 1 баре это приводит к точке b с температурой 270  К. Таким образом, дросселирование от 200 бар до 1 бар дает охлаждение от комнатной температуры до температуры ниже точки замерзания воды. Дросселирование от 200 бар и начальной температуры 133  К (точка c на рис. 2) до 1 бар приводит к точке d, которая находится в двухфазной области азота при температуре 77,2  К. Поскольку энтальпия является экстенсивным параметром, энтальпия в d ( h _d ) равна энтальпии в e ( h _e ), умноженной на массовую долю жидкости в d ( x _d ), плюс энтальпия в f ( h _f ), умноженная на массовую долю газа в d (1 − x _d ). Таким образом,

${\displaystyle h_{d}=x_{d}h_{e}+(1-x_{d})h_{f}.}$

С числами: 150 = x _d 28 + (1 − x _d ) 230, поэтому x _d составляет около 0,40. Это означает, что массовая доля жидкости в смеси жидкости и газа, выходящей из дроссельного клапана, составляет 40%.

Вывод коэффициента Джоуля-Томсона

Трудно физически представить, что представляет собой коэффициент Джоуля–Томсона, . Кроме того, современные определения не используют оригинальный метод, использованный Джоулем и Томсоном, а вместо этого измеряют другую, тесно связанную величину. ^[23] Таким образом, полезно вывести соотношения между и другими, более удобно измеряемыми величинами, как описано ниже. ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle \mu _{\mathrm {JT} }}$

Первый шаг в получении этих результатов — отметить, что коэффициент Джоуля–Томсона включает три переменные T , P и H. Полезный результат немедленно получается путем применения циклического правила ; в терминах этих трех переменных это правило можно записать

${\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{H}\left({\frac {\partial H}{\partial T}}\right)_{P}\left({\frac {\partial P}{\partial H}}\right)_{T}=-1.}$

Каждая из трех частных производных в этом выражении имеет определенное значение. Первая — , вторая — постоянная теплоемкость давления , , определяемая как ${\displaystyle \mu _{\mathrm {JT} }}$ ${\displaystyle C_{\mathrm {p} }}$

${\displaystyle C_{\mathrm {p} }=\left({\frac {\partial H}{\partial T}}\right)_{P}}$

и третий — обратный изотермический коэффициент Джоуля–Томсона , определяемый как ${\displaystyle \mu _{\mathrm {T} }}$

${\displaystyle \mu _{\mathrm {T} }=\left({\frac {\partial H}{\partial P}}\right)_{T}}$.

Эту последнюю величину легче измерить, чем . ^{[24] [25]} Таким образом, выражение из циклического правила становится ${\displaystyle \mu _{\mathrm {JT} }}$

${\displaystyle \mu _{\mathrm {JT} }=-{\frac {\mu _{\mathrm {T} }}{C_{p}}}.}$

Это уравнение можно использовать для получения коэффициентов Джоуля–Томсона из более легко измеряемого изотермического коэффициента Джоуля–Томсона. Оно используется далее для получения математического выражения для коэффициента Джоуля–Томсона в терминах объемных свойств жидкости.

Чтобы двигаться дальше, отправной точкой является фундаментальное уравнение термодинамики в терминах энтальпии; это

${\displaystyle \mathrm {d} H=T\mathrm {d} S+V\mathrm {d} P.}$

Теперь «разделив» на d P , при постоянной температуре, получаем

${\displaystyle \left({\frac {\partial H}{\partial P}}\right)_{T}=T\left({\frac {\partial S}{\partial P}}\right)_{T}+V}$

Частная производная слева — это изотермический коэффициент Джоуля-Томсона, , а справа можно выразить через коэффициент теплового расширения с помощью соотношения Максвелла . Соответствующее соотношение имеет вид ${\displaystyle \mu _{\mathrm {T} }}$

${\displaystyle \left({\frac {\partial S}{\partial P}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{P}=-V\alpha \,}$

где α — кубический коэффициент теплового расширения . Замена этих двух частных производных дает

${\displaystyle \mu _{\mathrm {T} }=-TV\alpha \ +V.}$

Это выражение теперь можно заменить в предыдущем уравнении, чтобы получить: ${\displaystyle \mu _{\mathrm {T} }}$ ${\displaystyle \mu _{\mathrm {JT} }}$

${\displaystyle \mu _{\mathrm {JT} }\equiv \left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}(\alpha T-1).\,}$

Это дает выражение для коэффициента Джоуля-Томсона в терминах общедоступных свойств теплоемкости, молярного объема и коэффициента теплового расширения. Это показывает, что температура инверсии Джоуля-Томсона, при которой равна нулю, возникает, когда коэффициент теплового расширения равен обратной величине температуры. Поскольку это справедливо при всех температурах для идеальных газов (см. расширение в газах ), коэффициент Джоуля-Томсона идеального газа равен нулю при всех температурах. ^[26] ${\displaystyle \mu _{\mathrm {JT} }}$

Второй закон Джоуля

Легко проверить, что для идеального газа, определяемого подходящими микроскопическими постулатами, αT = 1, поэтому изменение температуры такого идеального газа при расширении Джоуля–Томсона равно нулю. Для такого идеального газа этот теоретический результат подразумевает, что:

Внутренняя энергия фиксированной массы идеального газа зависит только от его температуры (а не от давления или объема).

Это правило было первоначально обнаружено Джоулем экспериментально для реальных газов и известно как второй закон Джоуля . Более точные эксперименты обнаружили важные отклонения от него. ^{[27] [28] [29]}

Смотрите также

• Критическая точка (термодинамика)
• Энтальпия и изентальпийный процесс
• Идеальный газ
• Сжижение газов
• MIRI (инструмент среднего инфракрасного диапазона) , петля Джоуля-Томпсона, используется в одном из инструментов космического телескопа Джеймса Уэбба.
• Охлаждение
• Обратимый процесс (термодинамика)

Ссылки

1. RH Perry и DW Green (1984). Справочник инженеров-химиков Перри . McGraw-Hill. ISBN 978-0-07-049479-4.
2. BN Roy (2002). Основы классической и статистической термодинамики . John Wiley & Sons. Bibcode :2002fcst.book.....N. ISBN 978-0-470-84313-0.
3. WC Edmister, BI Lee (1984). Прикладная термодинамика углеводородов . Том 1 (2-е изд.). Gulf Publishing. ISBN 978-0-87201-855-6.
4. Ф. Рейф (1965). "Глава 5 – Простые приложения макроскопической термодинамики". Основы статистической и тепловой физики . McGraw-Hill. ISBN 978-0-07-051800-1.
5. AW Adamson (1973). "Глава 4 – Химическая термодинамика. Первый закон термодинамики". Учебник физической химии (1-е изд.). Academic Press. LCCN  72088328.
6. GW Castellan (1971). "Глава 7 – Энергия и первый закон термодинамики; Термохимия". Физическая химия (2-е изд.). Addison-Wesley. ISBN 978-0-201-00912-5.
7. Моран, М. Дж.; Шапиро, Х. Н. (2006). Основы инженерной термодинамики (5-е изд.). John Wiley & Sons.
8. De Waele, ATAM (2017). «Основы сжижения Джоуля–Томсона и охлаждения Джоуля–Томсона». Журнал физики низких температур . 186 (5–6): 385–403. Bibcode :2017JLTP..186..385D. doi : 10.1007/s10909-016-1733-3 .
9. Pippard, Alfred B. (1981). Элементы классической термодинамики: для продвинутых студентов физики (Повторное издание). Cambridge: Univ. Pr. стр. 74–77. ISBN 978-0-521-09101-5.
10. Goussard, Jacques-Olivier; Roulet, Bernard (1993). «Свободное расширение для реальных газов». American Journal of Physics . 61 (9): 845–848. Bibcode : 1993AmJPh..61..845G. doi : 10.1119/1.17417.
11. Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: WH Freeman and Co. стр. 930. ISBN 978-0-7167-2871-9.
12. Рок, Пенсильвания (1983). Химическая термодинамика . Mill Valley, Калифорния: University Science Books. раздел 3-2. ISBN 978-0-935702-12-5.
13. Пиппард, AB (1957). «Элементы классической термодинамики», стр. 73. Cambridge University Press, Кембридж, Великобритания
14. Табор, Д. (1991). Газы, жидкости и твердые тела , стр. 148. Cambridge University Press, Кембридж, Великобритания ISBN 0 521 40667 6 . 
15. Клотц, IM и RM Розенберг (1991). Химическая термодинамика , стр. 83. Бенджамин, Мено Парк, Калифорния.
16. Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: WH Freeman and Co. стр. 31–32. ISBN 0-7167-2871-0 . 
17. Hoover, Wm. G.; Hoover, Carol G.; Travis, Karl P. (2014). «Ударно-волновое сжатие и расширение Джоуля–Томсона». Physical Review Letters . 112 (14): 144504. arXiv : 1311.1717 . Bibcode : 2014PhRvL.112n4504H. doi : 10.1103/PhysRevLett.112.144504. PMID  24765974. S2CID  33580985.
18. WR Salzman. "Джоулево расширение". Кафедра химии, Университет Аризоны . Архивировано из оригинала 13 июня 2012 года . Получено 23 июля 2005 года .
19. "10.3: Эксперимент Джоуля-Томсона". Physics LibreTexts . 25 января 2017 г. Получено 5 июля 2023 г.
20. Кинан, Дж. Х. (1970). Термодинамика , Глава 15. MIT Press, Кембридж, Массачусетс.
21. См., например, MJ Moran и HN Shapiro «Основы инженерной термодинамики», 5-е издание (2006) John Wiley & Sons, Inc., стр. 147.
22. Рисунок составлен на основе данных, полученных с помощью RefProp, NIST Standard Reference Database 23
23. Аткинс, Питер (1997). Физическая химия (6-е изд.). Нью-Йорк: WH Freeman and Co. стр. 89–90. ISBN 978-0-7167-2871-9.
24. Киз, Ф. Г.; Коллинз, С. К. (1932). «Изменение давления тепловой функции как прямая мера сил Ван-дер-Ваальса». Proc. Natl. Acad. Sci. USA . 18 (4): 328–333. Bibcode : 1932PNAS...18..328K. doi : 10.1073/pnas.18.4.328 . PMC 1076221. PMID  16587688. 
25. Cusco, L.; McBain, SE; Saville, G. (1995). «Проточный калориметр для измерения изотермического коэффициента Джоуля–Томсона газов при повышенных температурах и давлениях. Результаты для азота при температурах до 473 К и давлениях до 10 МПа и для диоксида углерода при температурах до 500 К и давлениях до 5 МПа». Журнал химической термодинамики . 27 (7): 721–733. doi :10.1006/jcht.1995.0073.
26. Каллен, Х. Б. (1960). Термодинамика . Нью-Йорк: John Wiley and Sons. С. 112–114.
27. Партингтон, Дж. Р. (1949). Расширенный трактат по физической химии , том 1 «Основные принципы». Свойства газов , Longmans, Green and Co. , Лондон, стр. 614–615.
28. Адкинс, К. Дж. (1968/1983). Равновесная термодинамика , (1-е издание 1968), третье издание 1983, Cambridge University Press, Кембридж, Великобритания, ISBN 0-521-25445-0 , стр. 116. 
29. Бейлин, М. (1994). Обзор термодинамики , Издательство Американского института физики, Нью-Йорк, ISBN 0-88318-797-3 , стр. 81. 

Библиография

• MW Zemansky (1968). Тепло и термодинамика; Учебник для среднего уровня . McGraw-Hill. С. 182, 355. LCCN  67026891.
• DV Schroeder (2000). Введение в тепловую физику . Addison Wesley Longman. стр. 142. ISBN 978-0-201-38027-9.
• C. Kittel, H. Kroemer (1980). Теплофизика . WH Freeman. ISBN 978-0-7167-1088-2.

Внешние ссылки

• Вайсштейн, Эрик Вольфганг (ред.). «Процесс Джоуля-Томсона». Мир Науки .
• Вайсштейн, Эрик Вольфганг (ред.). «Коэффициент Джоуля-Томсона». Мир Науки .
• «Кривая инверсии эффекта Джоуля-Томсона с использованием CEOS Пенга-Робинсона». Демонстрационные проекты Wolfram Mathematica .
• Модуль эффекта Джоуля-Томсона, Университет Нотр-Дам