stringtranslate.com

Ангемитоническая шкала

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 6/4 dfgacd } }
Звукоряд минъё на D, [1] эквивалентен звукоряду ё на C, [2] ангемитонический звукоряд
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 6/4 d ees ga bes d } }
Звукоряд Мияко-буши на D, эквивалентный звукоряду на D, [3] гемитонный звукоряд

Музыковедение обычно классифицирует гаммы как гемитонические или ангемитонические . Гемитонические гаммы содержат один или несколько полутонов , в то время как ангемитонические гаммы не содержат полутонов. Например, в традиционной японской музыке ангемитоническая гамма йо противопоставляется гемитонической в ​​гамме . [4] Самая простая и наиболее часто используемая гамма в мире — атритоническая ангемитоническая «мажорная» пентатоническая гамма . Целотонная гамма также является ангемитонической.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 7/4 cd ees fis g aes bc } }
Венгерская минорная гамма на C, когемитонная гамма. [5]

Особый подкласс гемитонных гамм — когемитонные гаммы. [6] Когемитонные гаммы содержат два или более полутонов (что делает их гемитоническими), так что два или более полутонов появляются последовательно в порядке гаммы. Например, венгерская минорная гамма в C включает F ♯ , G и A ♭ в этом порядке, с полутоном между F ♯ и G, а затем полутоном между G и A ♭ .

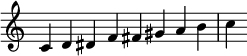
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 8/4 cd dis f fis gis abc } }
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 8/4 c des ees e ges ga bes c } }
Октатонические гаммы на C, гемитонические, но анкогемитонические

Анкогемитонические гаммы, напротив, либо не содержат полутонов (и, таким образом, являются ангемитоническими), либо содержат полутоны (будучи гемитоническими), где ни один из полутонов не появляется последовательно в порядке гаммы. [7] [ неудачная проверка ] Некоторые авторы, однако, не включают ангемитонические гаммы в свое определение анкогемитонических гамм. Примеров анкогемитонических гамм много, поскольку анкогемитония предпочтительнее когемитонии в мировой музыке: диатоническая гамма , мелодический мажор/ мелодический минор , гармоническая мажорная гамма , гармоническая минорная гамма , венгерская мажорная гамма , румынская мажорная гамма и так называемая октатоническая гамма .

Гемитония также количественно определяется количеством присутствующих полутонов. Негемитонические гаммы имеют только один полутон; дигемитонические гаммы имеют 2 полутона; тригемитонические гаммы имеют 3 полутона и т. д. Точно так же, как ангемитоническая гамма менее диссонантна, чем гемитоническая, ангемитоническая гамма менее диссонантна, чем дигемитоническая.

Квалификация когемитонии против анкогемитонии сочетается с мощностью полутонов, давая такие термины, как: дикогемитонический, триакогемитонический и т. д. Анкогемитонический звукоряд менее диссонансен, чем когемитонический, количество их полутонов одинаково. В общем, количество полутонов более важно для восприятия диссонанса, чем смежность (или ее отсутствие) любой пары из них. Дополнительная смежность между полутонами (если смежность присутствует) не обязательно увеличивает диссонанс, количество полутонов снова одинаково. [8]

С этими полутоновыми классификациями связаны тритонические и атритонические гаммы. Тритонические гаммы содержат один или несколько тритонов , тогда как атритонические гаммы не содержат тритонов. Между полутонами и тритонами существует особая монотонная связь, поскольку гаммы строятся проекцией, см. ниже.

Гармоническое отношение всех этих категорий исходит из восприятия того, что полутоны и тритоны являются самыми сильными диссонансами , и что часто желательно избегать их. Наиболее используемые гаммы на планете — ангемитонические. Из оставшихся гемитонических гамм наиболее используемые — анкогемитонические.

Количественная оценка гемитонии и ее связь с анкогемитонией

Большая часть музыки в мире является ангемитонической, возможно, 90%. [9] Из этой другой гемитонной части, возможно, 90% являются ангемитоническими, преобладающими в аккордах всего в 1 полутон, все из которых являются анкогемитоническими по определению. [9] Из оставшихся 10%, возможно, 90% являются дигемитоническими, преобладающими в аккордах не более чем в 2 полутона. То же самое относится к аккордам в 3 полутона. [10] В обоих последних случаях, однако, существует явное предпочтение анкогемитонии, поскольку отсутствие смежности любых двух полутонов во многом способствует смягчению нарастающего диссонанса.

В следующей таблице показан размер звучности (внизу слева) против количества полутонов (справа) плюс качество анкогемитонии (обозначается буквой A) против когемитонии (обозначается буквой C). В целом, анкогемитонических комбинаций меньше для данного аккорда или размера гаммы, но они используются гораздо чаще, поэтому их названия хорошо известны.

Столбец "0" представляет наиболее часто используемые аккорды., [8] избегая интервалов M7 и хроматических 9-х и таких комбинаций 4-х, хроматических 5-х и 6-х для получения полутонов. Столбец 1 представляет аккорды, которые едва используют гармонические ступени, которых избегает столбец "0". Однако столбец 2 представляет звуки, которые гораздо более трудно поддаются обработке. [8]

Столбец 0, строка 5 — полные, но приятные аккорды: 9-я, 6/9 и 9-альтернирующая5 без 7. [11] Столбец «0», строка «6», — уникальная целотонная гамма . [12] [ требуется проверка ] Столбец «2A», строка «7», локальный минимум, относится к диатонической гамме и мелодическим мажорным/ мелодическим минорным гаммам. [13] [ требуется проверка ] Анкогемитония, inter alii, вероятно, делает эти гаммы популярными. Столбец «2C», строка «7», другой локальный минимум, относится к неаполитанской мажорной гамме , которая является когемитонной и несколько менее распространенной, но все еще достаточно популярной, чтобы носить название. [14] [ требуется проверка ] Столбец «3A», строка «7», другой локальный минимум, представляет гармоническую мажорную гамму и ее инволюционную гармоническую минорную гамму , а также венгерскую мажорную гамму и ее инволюционную румынскую мажорную гамму . [15] [ требуется проверка ] Столбец «3A», строка «6», представляют собой гексатонические аналоги этих четырех знакомых гамм, [16] [ требуется проверка ] одна из которых является увеличенной гаммой , [17] [ требуется проверка ] а другой является аналогом октатонической гаммы - которая сама по себе появляется, одна и обособленно, в столбце ">=4A". строка «8». [18] [ =4A строка 8. (январь 2020 г.)"> требуется проверка ] Столбец «2A», строка «4», еще один минимум, представляет собой несколько откровенно диссонирующих, но странно резонирующих гармонических комбинаций: mM9 без 5, 11 ♭ 9, dom13 ♭ 9 и M7 ♯ 11. [11]

Обратите внимание также, что в строке с наивысшей кардинальностью для каждого столбца до начала конечных нулей, количество звучности невелико, за исключением строки "7" и столбцов "3" всех видов. Этот взрыв гемитонных возможностей, связанный с кардинальностью нот 7 (и выше), возможно, отмечает нижнюю границу для сущности, называемой "гаммой" (в отличие от "аккорда").

Как показано в таблице, ангемитония является свойством домена нотных наборов с кардинальностью от 2 до 6, тогда как анкогемитония является свойством домена нотных наборов с кардинальностью от 4 до 8 (от 3 до 8 для неправильной анкогемитонии, включая также ангемитонию). Это помещает ангемитонию в целом в диапазон «аккордов», а анкогемитонию в целом в диапазон «гамм».

Пример: гемитония и тритония чистой квинтовой проекции

Взаимосвязь полутонов, тритонов и увеличивающегося количества нот можно продемонстрировать, взяв пять последовательных тонов из квинтового круга ; [19] начиная с C, это C, G, D, A и E. Транспонирование тонов так, чтобы они вписывались в одну октаву, перестраивает их в мажорную пентатоническую гамму : C, D, E, G, A. Эта гамма является ангемитонической, не имеющей полутонов; она является атритонической, не имеющей тритонов.

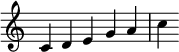
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 5/4 cdegac } }

Кроме того, это максимальное количество нот, взятых последовательно из квинтового круга, для которых еще возможно избежать полутона. [20]

Добавление еще одной ноты из квинтового круга дает мажорную гексатоническую гамму: CDEGA B. Эта гамма является гемитонной, то есть имеет полутон между B и C; она является атритонической, то есть не имеет тритонов. Кроме того, это максимальное количество нот, взятых последовательно из квинтового круга, для которых все еще возможно избежать тритона. [21] [ не удалось проверить ]

Добавление еще одной ноты из квинтового круга дает мажорную гептатоническую гамму: CDEFGAB (когда квинта добавляется из-под тоники). Эта гамма строго анкогемитоническая, имеющая 2 полутона, но не последовательные; она тритоническая, имеющая тритон между F и B. После этой точки в проекционном ряду к анализу вектора интервалов гаммы не добавляются новые интервалы [22] , но получается когемитония.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 7/4 cdefgabc } }
P7 проекция/большая гептатоника на C

Добавление еще одной ноты из квинтового круга дает мажорную октатоническую гамму: CDEFF ♯ GAB (когда квинта добавляется сверху верхней ноты в серии — в данном случае B). Эта гамма является когемитонической, имеющей 3 полутона вместе в EFF ♯ G, а также тритонической. [22] [ не удалось проверить ]

Подобное поведение наблюдается во всех гаммах в целом, что больше нот в шкале имеет тенденцию кумулятивно добавлять диссонансные интервалы (в частности: гемитония и тритония без определенного порядка) и когемитония, которых еще нет. Хотя также верно, что больше нот в шкале имеет тенденцию допускать больше и разнообразных интервалов в интервальном векторе , можно сказать, что существует точка убывающей отдачи , когда она квалифицируется против также увеличивающегося диссонанса, гемитонии, тритонии и когемитонии. [22] Именно около этих точек лежат самые популярные гаммы.

Когемитонные и гемитонные гаммы

Хотя когемитонические гаммы используются реже, чем анкогемитонические, они обладают интересным свойством. Последовательность двух (или более) последовательных полутонов в гамме дает возможность «разделить» гамму, поместив тонику гаммы на среднюю ноту полутонового диапазона. Это позволяет ведущему тону снизу разрешаться вверх, а также нисходящему бемольно-супертоническому верхнему соседу , оба сходятся на тонике. Разделение превращает слабость — диссонанс когемитонии — в силу: контрапунктическую конвергенцию на тонике. Очень часто когемитонная (или даже гемитонная) гамма (например, венгерская минорная { CDE ♭ F ♯ GA ♭ B }) смещается преимущественно в лад, в котором полутоновый диапазон разделен (например, двойная гармоническая гамма { GA ♭ BCDE ♭ F ♯ }), и под этим названием мы обычно знаем тот же круговой ряд интервалов. [23] Когемитонные гаммы с несколькими полутоновыми диапазонами предоставляют дополнительную возможность модуляции между тониками, каждая из которых снабжена как верхними, так и нижними соседями.

Модусы гептатонических гамм и система ключевых знаков

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key a \major s1 } }
Ключевой знак Ля мажор / Фа ♯ минор , анкогемитонная гептатоническая гамма.

Система ключевых знаков западной музыки основана на предположении о гептатонической гамме из 7 нот, так что в действительной ключевой подписи никогда не присутствует более 7 знаков альтерации. Глобальное предпочтение ангемитоническим гаммам сочетается с этой основой, чтобы выделить 6 анкогемитонических гептатонических гамм, [24] [ требуется проверка ] большинство из которых распространены в романтической музыке , и из которых состоит большая часть романтической музыки:

Эти когемитонные шкалы встречаются реже:

Придерживаясь определения гептатонических гамм, все они обладают 7 модами каждая и подходят для использования в модальной мутации . [25] Они представлены в таблице выше в строке «7», столбцах «2A» и «3A».

Таблица ключевых подписей

Ниже приведен список тональностей для всех возможных нетранспонированных ладов вышеупомянутых гептатонических гамм, использующих ноту C в качестве тоники.

Распространенное цитирование в теориях

Разное

Ссылки

  1. ^ Сьюзан Миё Асаи (1999). Танцевальная драма Номаи , с. 126. ISBN 978-0-313-30698-3 . 
  2. ^ Минору Мики, Марти Реган, Филип Флавин (2008). Сочинение для японских инструментов , стр. 2. ISBN 978-1-58046-273-0 . 
  3. ^ Титон, Джефф Тодд (1996). Миры музыки: Введение в музыку народов мира , стр. 373. ISBN 0-02-872612-X . 
  4. ↑ Anon. (2001) «Ditonus», The New Grove Dictionary of Music and Musicians , второе издание, под редакцией Стэнли Сейди и Джона Тиррелла . Лондон: Macmillan Publishers; Бенс Сабольчи (1943), «Пятитоновые гаммы и цивилизация», Acta Musicologica 15, Fasc. 1/4 (январь–декабрь): стр. 24–34, цитата на стр. 25.
  5. ^ Кахан, Сильвия (2009). В поисках новых масштабов , стр. 39. ISBN 978-1-58046-305-8 . Цитирует Листа. Des Bohémians , стр. 301. 
  6. ^ Крайст, Уильям (1966). Материалы и структура музыки , т. 1, стр. 39. Englewood Cliffs: Prentice–Hall. LOC 66-14354.
  7. ^ Тимочко, Дмитрий (1997). «Ограничение последовательных полутонов на скалярной структуре: связь между импрессионизмом и джазом», Integral , т. 11, (1997), стр. 135-179.
  8. ^ abc Кит, Майкл. 1991. От полихордов к полиа: приключения в музыкальной комбинаторике , стр. 45. Принстон: Vinculum Press. ISBN 978-0963009708 . 
  9. ^ ab Кейт, Майкл. 1991. От полихордов к полиа: приключения в музыкальной комбинаторике , стр. 43. Принстон: Vinculum Press. ISBN 978-0963009708 . 
  10. ^ Кит, Майкл. 1991. От полихордов к полиа: приключения в музыкальной комбинаторике , стр. 48-49. Принстон: Vinculum Press. ISBN 978-0963009708 . 
  11. ^ ab Wilmott, Brett. (1994) Полная книга Мэла Бэя по теории гармонии и голосоведению , стр. 210. Pacific, Missouri: Mel Bay. ISBN 978-1562229948 . 
  12. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 367. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  13. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 362-363. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  14. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 363. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  15. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 364. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  16. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 369. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  17. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 368. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  18. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 360. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  19. ^ Купер, Пол. 1973. Перспективы в теории музыки: историко-аналитический подход , стр. 18. Нью-Йорк: Dodd, Mead. ISBN 0-396-06752-2 . 
  20. ^ Hanson, Howard. (1960) Harmonic Materials of Modern Music , стр. 29. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138. «Гексада [состоящая из чистых квинт] добавляет B, CGDAEB, или мелодически, производя CDEFGAB, ее компонентами являются пять чистых квинт, четыре больших секунды, три малых терции, две больших терции и — впервые — диссонирующая малая секунда (или большая септима), p 5 m 2 n 3 s 4 d ».
  21. ^ Хансон, Ховард. (1960) Гармонические материалы современной музыки , стр. 40. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  22. ^ abc Hanson, Howard. (1960) Harmonic Materials of Modern Music , стр. 33. New York: Appleton-Century-Crofts. LOC 58-8138. "Когда проекция [чистой квинты] переносится за пределы семи тонов, новые интервалы не могут быть добавлены". "С другой стороны, поскольку звучности проецируются за пределы шеститоновой серии, они имеют тенденцию терять свою индивидуальность. Все семитоновые серии, например, содержат все шесть основных интервалов, и разница в их пропорции уменьшается по мере добавления дополнительных тонов... Такие модели имеют тенденцию терять свою индивидуальность, создавая монохроматический эффект с сопутствующим ему отсутствием существенного элемента контраста".
  23. ^ Шиллингер, Джозеф. (1941) Система музыкальной композиции Шиллингера , т.1, с. 113 и далее. Нью-Йорк: Карл Фишер. ISBN 0306775212 . 
  24. ^ abcdefghij Хансон, Говард. (1960) Гармонические материалы современной музыки , стр. 362 и далее. Нью-Йорк: Appleton-Century-Crofts. LOC 58-8138.
  25. ^ Крайст, Уильям (1966). Материалы и структура музыки , т. 1, стр. 45. Englewood Cliffs: Prentice-Hall. LOC 66-14354.