Средняя аномалия

Определяет орбиту объекта в космосе.

Площадь, подметаемая за единицу времени  объектом на эллиптической орбите , и  воображаемым объектом на круговой орбите (с одинаковым орбитальным периодом). Оба выметают равные площади за одинаковое время, но угловая скорость выметания меняется для эллиптической орбиты и постоянна для круговой орбиты. Показаны средняя аномалия и истинная аномалия для двух единиц времени. (Обратите внимание, что для визуальной простоты на схеме изображена неперекрывающаяся круговая орбита, поэтому эта круговая орбита с одинаковым орбитальным периодом не показана в истинном масштабе с этой эллиптической орбитой: чтобы масштаб был истинным для двух орбит с равным периодом, эти орбиты должны пересекаться.)

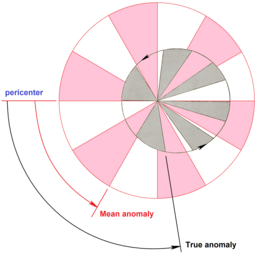
В небесной механике средняя аномалия — это часть периода эллиптической орбиты , которая прошла с тех пор, как вращающееся тело прошло перицентр , выраженная в виде угла , который может быть использован при вычислении положения этого тела в классической задаче двух тел . Это угловое расстояние от перицентра , которое имело бы фиктивное тело, если бы оно двигалось по круговой орбите с постоянной скоростью в тот же орбитальный период , что и фактическое тело на своей эллиптической орбите. ^{[1] [2]}

Определение

Определим T как время, необходимое для того, чтобы конкретное тело завершило один оборот. За время T радиус -вектор проходит 2 π радиан, или 360°. Средняя скорость прохождения, n , тогда равна

$${\displaystyle n={\frac {\,2\,\pi \,}{T}}={\frac {\,360^{\circ }\,}{T}}~,}$$

которое называется средним угловым движением тела и имеет размерность радиан в единицу времени или градусов в единицу времени.

Определим τ как время, в которое тело находится в перицентре. Из приведенных выше определений можно определить новую величину M , среднюю аномалию

$${\displaystyle M=n\,(t-\tau )~,}$$

что дает угловое расстояние от перицентра в произвольный момент времени t ^[3] с размерностью в радианах или градусах.

Поскольку скорость увеличения, n , является постоянным средним значением, средняя аномалия увеличивается равномерно (линейно) от 0 до 2 π радиан или от 0° до 360° в течение каждой орбиты. Она равна 0, когда тело находится в перицентре, π радиан (180°) в апоцентре и 2 π радиан (360°) после одного полного оборота. ^[4] Если средняя аномалия известна в любой данный момент, ее можно вычислить в любой более поздний (или предыдущий) момент, просто прибавив (или вычтя) n⋅δt , где δt представляет собой небольшую разницу во времени.

Средняя аномалия не измеряет угол между какими-либо физическими объектами (за исключением перицентра или апоцентра, или для круговой орбиты). Это просто удобная единая мера того, насколько далеко по своей орбите продвинулось тело с перицентра. Средняя аномалия — один из трех угловых параметров (исторически известных как «аномалии»), которые определяют положение вдоль орбиты, два других — эксцентрическая аномалия и истинная аномалия .

Средняя аномалия в эпоху

Средняя аномалия в эпоху , M ₀ , определяется как мгновенная средняя аномалия в заданную эпоху , t ₀ . Это значение иногда предоставляется с другими орбитальными элементами, чтобы обеспечить возможность вычислений прошлых и будущих положений объекта вдоль орбиты. Эпоха, для которой определен M _{0 ,} часто определяется соглашением в данной области или дисциплине. Например, планетарные эфемериды часто определяют M ₀ для эпохи J2000 , в то время как для объектов на орбите Земли, описываемых двухстрочным набором элементов, эпоха указывается как дата в первой строке. ^[5]

Формулы

Среднюю аномалию M можно вычислить из эксцентрической аномалии E и эксцентриситета e с помощью уравнения Кеплера :

$${\displaystyle M=E-e\,\sin E~.}$$

Средняя аномалия также часто рассматривается как

$${\displaystyle M=M_{0}+n\left(t-t_{0}\right)~,}$$

где M ₀ — средняя аномалия в эпоху t ₀ , которая может совпадать или не совпадать с τ , временем прохождения перицентра. Классический метод нахождения положения объекта на эллиптической орбите из набора орбитальных элементов заключается в вычислении средней аномалии по этому уравнению, а затем в решении уравнения Кеплера для эксцентрической аномалии.

Определим ϖ как долготу перицентра , угловое расстояние перицентра от опорного направления. Определим ℓ как среднюю долготу , угловое расстояние тела от того же опорного направления, предполагая, что оно движется с равномерным угловым движением, как и средняя аномалия. Таким образом, средняя аномалия также ^[6]

$${\displaystyle M=\ell -\varpi ~.}$$

Среднее угловое движение также можно выразить,

$${\displaystyle n={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}~,}$$

где μ — гравитационный параметр , который меняется в зависимости от массы объектов, а a — большая полуось орбиты. Затем среднюю аномалию можно разложить,

$${\displaystyle M={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}\,\left(t-\tau \right)~,}$$

и здесь средняя аномалия представляет собой равномерное угловое движение по окружности радиуса a . ^[7]

Средняя аномалия может быть рассчитана из эксцентриситета и истинной аномалии f путем нахождения эксцентрической аномалии и последующего использования уравнения Кеплера. Это дает в радианах: где atan2 (y, x) — угол между осью x и лучом из (0, 0) в (x, y), имеющий тот же знак, что и y. $${\displaystyle M=\operatorname {atan2} \left(-\ {\sqrt {1-e^{2}}}\sin f,-\ e-\cos f\right)+\pi -e{\frac {{\sqrt {1-e^{2}}}\sin f}{1+e\cos f}}}$$

Для параболических и гиперболических траекторий средняя аномалия не определена, поскольку у них нет периода. Но в этих случаях, как и в случае эллиптических орбит, площадь, заметаемая хордой между аттрактором и объектом, следующим по траектории, линейно увеличивается со временем. Для гиперболического случая существует формула, аналогичная приведенной выше, дающая прошедшее время как функцию угла (истинная аномалия в эллиптическом случае), как объяснено в статье Орбита Кеплера . Для параболического случая существует другая формула, предельный случай либо для эллиптического, либо для гиперболического случая, когда расстояние между фокусами стремится к бесконечности – см. Параболическая траектория#Уравнение Баркера .

Среднее отклонение также можно выразить как расширение ряда : ^[8] $${\displaystyle M=f+2\sum _{n=1}^{\infty }(-1)^{n}\left[{\frac {1}{n}}+{\sqrt {1-e^{2}}}\right]\beta ^{n}\sin {nf}}$$

с ${\displaystyle \beta ={\frac {1-{\sqrt {1-e^{2}}}}{e}}}$

$${\displaystyle M=f-2\,e\sin f+\left({\frac {3}{4}}e^{2}+{\frac {1}{8}}e^{4}\right)\sin 2f-{\frac {1}{3}}e^{3}\sin 3f+{\frac {5}{32}}e^{4}\sin 4f+\operatorname {\mathcal {O}} \left(e^{5}\right)}$$

Подобная формула дает истинную аномалию непосредственно через среднюю аномалию: ^[9]

$${\displaystyle f=M+\left(2\,e-{\frac {1}{4}}e^{3}\right)\sin M+{\frac {5}{4}}e^{2}\sin 2M+{\frac {13}{12}}e^{3}\sin 3M+\operatorname {\mathcal {O}} \left(e^{4}\right)}$$

Общую формулировку приведенного выше уравнения можно записать как уравнение центра : ^[10]

$${\displaystyle f=M+2\sum _{s=1}^{\infty }{\frac {1}{s}}\left[J_{s}(se)+\sum _{p=1}^{\infty }\beta ^{p}{\big (}J_{s-p}(se)+J_{s+p}(se){\big )}\right]\sin(sM)}$$

Смотрите также

• Законы движения планет Кеплера
• Средняя долгота
• Среднее движение
• Орбитальные элементы

Ссылки

1. Монтенбрюк, Оливер (1989). Практические расчеты эфемерид . Springer-Verlag . стр. 44. ISBN 0-387-50704-3.
2. Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 182. ИСБН 0-943396-35-2.
3. Смарт, В. М. (1977). Учебник по сферической астрономии (шестое изд.). Cambridge University Press, Кембридж. стр. 113. ISBN 0-521-29180-1.
4. Миус (1991), стр. 183
5. "Space-Track.org". www.space-track.org . Получено 2024-08-19 .
6. Смарт (1977), стр. 122
7. Вальядо, Дэвид А. (2001). Основы астродинамики и ее применения (2-е изд.). Эль Сегундо, Калифорния: Microcosm Press. стр. 53–54. ISBN 1-881883-12-4.
8. Смарт, В. М. (1953). Небесная механика . Лондон, Великобритания: Longmans, Green, and Co. стр. 38.
9. Рой, AE (1988). Орбитальное движение (1-е изд.). Бристоль, Великобритания; Филадельфия, Пенсильвания: A. Hilger. ISBN 0852743602.
10. Брауэр, Дирк (1961). Методы небесной механики . Elsevier. стр. например, 77.

Внешние ссылки

• Глоссарий запись аномалия, среднее значение Архивировано 23.12.2017 на Wayback Machine в Астрономическом альманахе Военно-морской обсерватории США в Интернете Архивировано 20.04.2015 на Wayback Machine