Максимальная апостериорная оценка

Метод оценки параметров статистической модели

В байесовской статистике оценка максимальной апостериорной вероятности ( MAP ) — это оценка неизвестной величины, которая равна моде апостериорного распределения . MAP можно использовать для получения точечной оценки ненаблюдаемой величины на основе эмпирических данных. Он тесно связан с методом оценки максимального правдоподобия (ML), но использует расширенную цель оптимизации , которая включает априорное распределение (которое количественно определяет дополнительную информацию, доступную через априорное знание связанного события) по величине, которую требуется оценить. Поэтому оценку MAP можно рассматривать как регуляризацию оценки максимального правдоподобия.

Описание

Предположим, что мы хотим оценить ненаблюдаемый параметр популяции на основе наблюдений . Пусть будет распределением выборки , так что есть вероятность того, что базовый параметр популяции равен . Тогда функция: ${\displaystyle \theta }$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f(x\mid \theta )}$ ${\displaystyle x}$ ${\displaystyle \theta }$

${\displaystyle \theta \mapsto f(x\mid \theta )\!}$

известна как функция правдоподобия и оценка:

${\displaystyle {\hat {\theta }}_{\mathrm {MLE} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\!}$

является оценкой максимального правдоподобия . ${\displaystyle \theta }$

Теперь предположим, что существует априорное распределение по . Это позволяет нам обращаться со случайной величиной, как в байесовской статистике . Мы можем вычислить апостериорное распределение с помощью теоремы Байеса : ${\displaystyle g}$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle \theta }$

${\displaystyle \theta \mapsto f(\theta \mid x)={\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}\!}$

где — функция плотности , — область определения . ${\displaystyle g}$ ${\displaystyle \theta }$ ${\displaystyle \Theta }$ ${\displaystyle g}$

Метод максимальной апостериорной оценки затем оценивает моду апостериорного распределения этой случайной величины : ${\displaystyle \theta }$

${\displaystyle {\begin{aligned}{\hat {\theta }}_{\mathrm {MAP} }(x)&={\underset {\theta }{\operatorname {arg\,max} }}\ f(\theta \mid x)\\&={\underset {\theta }{\operatorname {arg\,max} }}\ {\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}\\&={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\,g(\theta ).\end{aligned}}\!}$

Знаменатель апостериорного распределения (так называемое предельное правдоподобие ) всегда положителен и не зависит от и, следовательно, не играет никакой роли в оптимизации. Обратите внимание, что оценка MAP совпадает с оценкой ML, когда априорная вероятность равномерна (т.е. является постоянной функцией ). ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle g}$ ${\displaystyle g}$

Когда функция потерь имеет вид

${\displaystyle L(\theta ,a)={\begin{cases}0,&{\text{if }}|a-\theta |<c,\\1,&{\text{otherwise}},\\\end{cases}}}$

При приближении к 0 байесовская оценка приближается к оценщику MAP, при условии, что распределение является квазивогнутым. ^[1] Однако, как правило, оценщик MAP не является байесовской оценкой, если только он не является дискретным . ${\displaystyle c}$ ${\displaystyle \theta }$ ${\displaystyle \theta }$

Вычисление

Оценки MAP можно рассчитать несколькими способами:

1. Аналитически, когда мода(ы) апостериорного распределения могут быть заданы в замкнутой форме . Это тот случай, когда используются сопряженные априорные распределения .
2. С помощью численной оптимизации, такой как метод сопряженных градиентов или метод Ньютона . Обычно для этого требуются первые или вторые производные , которые должны быть оценены аналитически или численно.
3. С помощью модификации алгоритма максимизации ожидания . Это не требует производных апостериорной плотности.
4. С помощью метода Монте-Карло с использованием имитации отжига

Ограничения

Хотя для оценки MAP требуются только мягкие условия, чтобы она была предельным случаем оценки Байеса (при функции потерь 0–1), ^[1] она не очень репрезентативна для байесовских методов в целом. Это связано с тем, что оценки MAP являются точечными оценками, тогда как байесовские методы характеризуются использованием распределений для обобщения данных и выведения выводов: таким образом, байесовские методы, как правило, сообщают апостериорное среднее или медиану вместо этого вместе с достоверными интервалами . Это связано как с тем, что эти оценщики оптимальны при квадратичной и линейной ошибке потерь соответственно, которые более репрезентативны для типичных функций потерь , так и с тем, что для непрерывного апостериорного распределения нет функции потерь, которая предполагает, что MAP является оптимальной точечной оценкой. Кроме того, апостериорное распределение часто может не иметь простой аналитической формы: в этом случае распределение можно моделировать с помощью методов Монте-Карло на основе цепей Маркова , в то время как оптимизация для нахождения его моды(-ей) может быть сложной или невозможной. ^{[ необходима цитата ]}

Пример плотности бимодального распределения , в котором наивысшая мода нехарактерна для большей части распределения

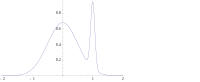
Во многих типах моделей, таких как модели смесей , апостериор может быть многомодальным . В таком случае обычно рекомендуют выбирать наивысшую моду: это не всегда осуществимо ( глобальная оптимизация — сложная проблема), а в некоторых случаях даже возможно (например, когда возникают проблемы с идентификацией ). Более того, наивысшая мода может быть нехарактерной для большинства апостериорных.

Наконец, в отличие от оценщиков ML, оценка MAP не инвариантна при репараметризации. Переключение с одной параметризации на другую подразумевает введение якобиана , который влияет на местоположение максимума. ^[2]

В качестве примера разницы между байесовскими оценками, упомянутыми выше (средние и медианные оценки), и использованием оценки MAP рассмотрим случай, когда необходимо классифицировать входные данные как положительные или отрицательные (например, кредиты как рискованные или безопасные). Предположим, что есть всего три возможных гипотезы о правильном методе классификации и с апостериорами 0,4, 0,3 и 0,3 соответственно. Предположим, что задан новый экземпляр, , классифицирует его как положительный, тогда как два других классифицируют его как отрицательный. Используя оценку MAP для правильного классификатора , классифицируется как положительный, тогда как байесовские оценки усреднили бы все гипотезы и классифицировали бы как отрицательный. ${\displaystyle x}$ ${\displaystyle h_{1}}$ ${\displaystyle h_{2}}$ ${\displaystyle h_{3}}$ ${\displaystyle x}$ ${\displaystyle h_{1}}$ ${\displaystyle h_{1}}$ ${\displaystyle x}$ ${\displaystyle x}$

Пример

Предположим, что нам дана последовательность случайных величин IID и априорное распределение задается как . Мы хотим найти оценку MAP для . Обратите внимание, что нормальное распределение является своим собственным сопряженным априорным распределением , поэтому мы сможем найти решение в замкнутой форме аналитически. ${\displaystyle (x_{1},\dots ,x_{n})}$ ${\displaystyle N(\mu ,\sigma _{v}^{2})}$ ${\displaystyle \mu }$ ${\displaystyle N(\mu _{0},\sigma _{m}^{2})}$ ${\displaystyle \mu }$

Тогда максимизируемая функция определяется как ^[3]

${\displaystyle g(\mu )f(x\mid \mu )=\pi (\mu )L(\mu )={\frac {1}{{\sqrt {2\pi }}\sigma _{m}}}\exp \left(-{\frac {1}{2}}\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}\right)\prod _{j=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma _{v}}}\exp \left(-{\frac {1}{2}}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}\right),}$

что эквивалентно минимизации следующей функции : ${\displaystyle \mu }$

${\displaystyle \sum _{j=1}^{n}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}+\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}.}$

Таким образом, мы видим, что оценка MAP для μ определяется выражением ^[3]

${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }={\frac {\sigma _{m}^{2}\,n}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\left({\frac {1}{n}}\sum _{j=1}^{n}x_{j}\right)+{\frac {\sigma _{v}^{2}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\,\mu _{0}={\frac {\sigma _{m}^{2}\left(\sum _{j=1}^{n}x_{j}\right)+\sigma _{v}^{2}\,\mu _{0}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}.}$

что оказывается линейной интерполяцией между априорным средним и выборочным средним, взвешенным по их соответствующим ковариациям.

Случай называется неинформативным априорным и приводит к неправильному распределению вероятностей ; в этом случае ${\displaystyle \sigma _{m}\to \infty }$ ${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }\to {\hat {\mu }}_{\mathrm {MLE} }.}$

Ссылки

1. Бассетт, Роберт; Дерид, Хулио (2018-01-30). «Максимальные апостериорные оценки как предел байесовских оценок». Математическое программирование : 1–16. arXiv : 1611.05917 . doi :10.1007/s10107-018-1241-0. ISSN  0025-5610.
2. Мерфи, Кевин П. (2012). Машинное обучение: вероятностная перспектива . Кембридж, Массачусетс: MIT Press. стр. 151–152. ISBN 978-0-262-01802-9.
3. Young, GA; Smith, RL (2005). Основы статистического вывода. Серия Cambridge по статистической и вероятностной математике. Кембридж: Cambridge University Press. ISBN 978-0-521-83971-6.

• ДеГрут, М. (1970). Оптимальные статистические решения . McGraw-Hill. ISBN 0-07-016242-5.
• Соренсон, Гарольд В. (1980). Оценка параметров: принципы и проблемы . Марсель Деккер. ISBN 0-8247-6987-2.
• Хальд, Андерс (2007). «Вывод нормального распределения Гауссом и метод наименьших квадратов, 1809». История параметрического статистического вывода от Бернулли до Фишера, 1713–1935 . Нью-Йорк: Springer. С. 55–61. ISBN 978-0-387-46409-1.