Элементарная арифметика

Числа и основные операции над ними

Символы для элементарных математических операций. С левого верхнего угла по часовой стрелке: сложение, деление, умножение и вычитание.

Элементарная арифметика — раздел математики , включающий сложение , вычитание , умножение и деление . Благодаря низкому уровню абстракции , широкому спектру применения и положению в качестве основы всей математики, элементарная арифметика обычно является первым разделом математики, преподаваемым в школах. ^{[1] [2]}

Системы счисления

В системах счисления цифры — это символы, используемые для представления значений чисел. Примером системы счисления является преимущественно используемая индо-арабская система счисления (от 0 до 9), которая использует десятичную позиционную систему счисления . ^[3] Другие системы счисления включают систему кактовик (часто используемую в эскимосско-алеутских языках Аляски , Канады и Гренландии ), которая является двадцатеричной позиционной системой счисления . ^[4] Независимо от используемой системы счисления, результаты арифметических операций не изменяются.

Функция преемника и упорядочивание

В элементарной арифметике последующее натуральное число (включая ноль) — это следующее натуральное число и является результатом прибавления единицы к этому числу. Предшественник натурального числа (исключая ноль) — это предыдущее натуральное число и является результатом вычитания единицы из этого числа. Например, последующее число нуля — это единица, а предшественник одиннадцати — это десять ( и ). Каждое натуральное число имеет последующее число, и каждое натуральное число, кроме 0, имеет предшественника. ^[5] ${\displaystyle 0+1=1}$ ${\displaystyle 11-1=10}$

Натуральные числа имеют общий порядок . Если одно число больше ( ) другого числа, то последнее меньше ( ) первого. Например, три меньше восьми ( ), поэтому восемь больше трех ( ). Натуральные числа также хорошо упорядочены , что означает, что любое подмножество натуральных чисел имеет наименьший элемент . ${\displaystyle >}$ ${\displaystyle <}$ ${\displaystyle 3<8}$ ${\displaystyle 8>3}$

Подсчет

Подсчет присваивает натуральное число каждому объекту в наборе , начиная с 1 для первого объекта и увеличивая на 1 для каждого последующего объекта. Количество объектов в наборе — это счетчик. Это также известно как мощность набора .

Подсчет также может быть процессом подсчета , процессом нанесения отметки на каждый предмет в наборе.

Добавление

Пример сложения с переносом . Черные числа — слагаемые, зеленое число — перенос, а синее число — сумма. В самой правой цифре сложение 9 и 7 равно 16, перенося 1 в следующую пару цифр слева, что делает сложение 1 + 5 + 2 = 8. Следовательно, 59 + 27 = 86.

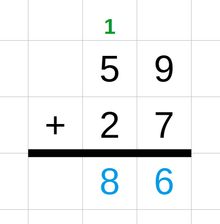
Сложение — это математическая операция, которая объединяет два или более чисел (называемых слагаемыми или слагаемыми) для получения объединенного числа (называемого суммой). Сложение двух чисел обозначается знаком плюс ( ). ^[6] Оно выполняется в соответствии со следующими правилами: ${\displaystyle +}$

• Порядок, в котором складывают слагаемые, не влияет на сумму. Это известно как коммутативное свойство сложения. (a + b) и (b + a) дают одинаковый результат. ^{[7] [8]}
• Сумма двух чисел уникальна; для суммы существует только один правильный ответ. ^[8]

Когда сумма пары цифр дает двузначное число, цифра «десяток» называется «цифрой переноса». ^[9] На уроках элементарной арифметики ученики обычно учатся складывать целые числа , а также могут изучать такие темы, как отрицательные числа и дроби .

Вычитание

Вычитание вычисляет разницу между двумя числами, где уменьшаемое — это число, из которого вычитается, а вычитаемое — это число, из которого вычитается. Оно представлено с помощью знака минус ( ). Знак минус также используется для обозначения отрицательных чисел. ${\displaystyle -}$

Вычитание не является коммутативным, что означает, что порядок чисел может изменить конечное значение; не то же самое, что . В элементарной арифметике уменьшаемое всегда больше вычитаемого, чтобы получить положительный результат. ${\displaystyle 3-5}$ ${\displaystyle 5-3}$

Вычитание также используется для разделения, объединения (например, для определения размера подмножества определенного множества) и нахождения величин в других контекстах.

Существует несколько методов выполнения вычитания. Традиционный математический метод вычитания использует методы, подходящие для ручного расчета. ^[10] Реформистская математика в целом отличается отсутствием предпочтения какой-либо конкретной методики, заменяясь руководством для студентов в изобретении их собственных методов вычисления.

В американских школах обучают методу вычитания с использованием заимствования. ^[11] Задача на вычитание, например, решается путем заимствования 10 из разряда десятков для прибавления к разряду единиц, чтобы облегчить вычитание. Вычитание 9 из 6 включает заимствование 10 из разряда десятков, превращая задачу в . Это обозначается зачеркиванием 8, написанием 7 над ней и написанием 1 над 6. Эти отметки называются «костылями», их изобрел Уильям А. Браунелл , который использовал их в исследовании в ноябре 1937 года. ^[12] ${\displaystyle 86-39}$ ${\displaystyle 70+16-39}$

Австрийский метод, также известный как метод сложения, преподается в некоторых европейских странах ^{[ какие? ]} . В отличие от предыдущего метода, заимствования не используются, хотя есть костыли, которые различаются в зависимости от некоторых стран. ^{[13] [14]} Метод сложения включает в себя увеличение вычитаемого. Это преобразует предыдущую задачу в . Маленькая 1 отмечена под вычитаемой цифрой в качестве напоминания. ${\displaystyle (80+16)-(39+10)}$

Пример

Вычитаем числа 792 и 308, начиная со столбца единиц, получаем, что 2 меньше 8. Используя метод заимствования, 10 заимствуется из 90, сокращая 90 до 80. Это меняет задачу на . ${\displaystyle 12-8}$

В столбце десятков разница между 80 и 0 составляет 80.

В столбце сотен разница между 700 и 300 составляет 400.

Результат:

${\displaystyle 792-308=484}$

Умножение

Умножение — это математическая операция многократного сложения. При умножении двух чисел результирующее значение является произведением. Умножаемые числа являются множимыми, множителями или факторами. Умножение может быть выражено как «пять раз три равно пятнадцати», «пять раз три равно пятнадцати» или «пятнадцать равно произведению пяти и трех».

Умножение обозначается знаком умножения (×), звездочкой (*), скобками () или точкой (⋅). Выражение «пять раз три равно пятнадцати» можно записать как « », « », « » или « ». ${\displaystyle 5\times 3=15}$ ${\displaystyle 5\ast 3=15}$ ${\displaystyle (5)(3)=15}$ ${\displaystyle 5\cdot 3=15}$

В элементарной арифметике умножение удовлетворяет следующим свойствам ^[a] :

• Коммутативность . Изменение порядка в произведении не меняет результат: . ${\displaystyle a\times b=b\times a}$
• Ассоциативность . Изменение порядка скобок в произведении не меняет результат: . ${\displaystyle a\times (b\times c)=(a\times b)\times c}$
• Распределительность . Умножение распределяет относительно сложения: . ${\displaystyle a\times (b+c)=a\times b+a\times c}$
• Тождество . Любое число, умноженное на 1, равно самому себе.
• Ноль . Любое число, умноженное на 0, равно 0.

В алгоритме умножения цифра «десятков» произведения пары цифр называется «цифрой переноса».

Пример умножения на однозначный множитель

Умножая 729 на 3, начиная со столбца единиц, получаем произведение 9 на 3, равное 27. 7 записывается под столбцом единиц, а 2 — над столбцом десятков в качестве переноса.

Произведение 2 и 3 равно 6, а цифра переноса добавляет 2 к 6, поэтому 8 записывается под колонкой десятков.

Произведение 7 и 3 равно 21, и поскольку это последняя цифра, 2 не будет записана как цифра переноса, а вместо этого будет записана рядом с 1.

Результат:

${\displaystyle 3\times 729=2187}$

Пример умножения многозначных множителей

Умножая 789 и 345, начиная со столбца единиц, получаем произведение 789 и 5, равное 3945.

4 — это десяток. Множитель — 40, а не 4. Произведение 789 и 40 равно 31560.

3 — в разряде сотен. Множитель — 300. Произведение 789 и 300 — 236700.

Добавляем все продукты,

Результат:

${\displaystyle 789\times 345=272205}$

Разделение

Деление — арифметическая операция, обратная умножению . Учитывая, что , , ${\displaystyle c\times b=a}$

Деление можно записать как , , или a ⁄ b . Это можно прочитать устно как « a разделить на b » или « a на b ». ${\displaystyle a\div b}$ ${\displaystyle {\frac {a}{b}}}$

В некоторых неанглоязычных культурах [ ^{каких ? ]} « a деленное на b » пишется как a  : b . В английском языке двоеточие ограничивается понятием отношения (« a is to b »).

В уравнении a — делимое, b — делитель, c — частное. Деление на ноль считается невозможным на уровне элементарной арифметики. ${\displaystyle a\div b=c}$

Два числа можно разделить на бумаге с помощью длинного деления . Сокращенная версия длинного деления, короткое деление , может использоваться для меньших делителей.

Менее систематический метод использует концепцию фрагментации , предполагающую вычитание большего количества кратных из частичного остатка на каждом этапе.

Пример

Разделив 272 и 8, начиная с цифры сотен, получаем, что 2 не делится на 8. Сложите 20 и 7, чтобы получить 27. Наибольшее число, на которое можно умножить делитель 8, не превысив 27, — это 3, поэтому оно записано под колонкой десятков. Вычитание 24 (произведения 3 и 8) из 27 дает остаток 3 .

Переходя к разряду единиц, получаем число 2. Сложение 30 (остаток 3, умноженный на 10) и 2 дает 32. Частное 32 и 8 равно 4, что записано под столбцом единиц.

Результат:

${\displaystyle 272\div 8=34}$

Метод остановки автобуса

Другим методом деления, которому учат в некоторых школах, является метод автобусной остановки, иногда обозначаемый как

   результат   (делитель) делимое

Ниже показаны шаги на том же примере, что и выше:

  0 3 4   8|272 0 ( 8 × 0 = 0) 2 7 ( 2 – 0 = 2 ) 24 ( 8 × 3 = 24) 3 2 (27 – 24 = 3 ) 32 ( 8 × 4 = 32) 0 (32 - 32 = 0)

Результат:

${\displaystyle 272\div 8=34}$

Образовательные стандарты

Элементарная арифметика обычно преподается на уровне начальной или средней школы и регулируется местными образовательными стандартами. В Соединенных Штатах и ​​Канаде ведутся дебаты о содержании и методах, используемых для обучения элементарной арифметике. ^{[15] [16]}

Смотрите также

• Раннее обучение счету
• Элементарная математика
• Разделение (фрагментация)
• Знаки плюс и минус
• Аксиомы Пеано
• Деление на ноль
• Реальное число
• Мнимое число
• Числовое предложение

Примечания

1. В то время как элементарная арифметика в основном работает с множеством натуральных чисел ( иногда включая 0), умножение с другими числовыми множествами может удовлетворять большему или меньшему количеству свойств, чем перечисленные здесь, например, наличие обратного элемента в рациональных числах и далее или отсутствие коммутативности в кватернионах и множествах чисел более высокого порядка.

Ссылки

1. Митчелмор, Майкл С.; Уайт, Пол (2012). Сил, Норберт М. (ред.). Абстракция в изучении математики. Бостон, Массачусетс: Springer US. стр. 31–33. doi :10.1007/978-1-4419-1428-6_516. ISBN 978-1-4419-1428-6.
2. Бьёрклунд, Камилла; Мартон, Ференс; Куллберг, Ангелика (2021). «Чему нужно научиться? Критические аспекты элементарных арифметических навыков». Educational Studies in Mathematics . 107 (2): 261–284. doi : 10.1007/s10649-021-10045-0 . ISSN  0013-1954.
3. "система счисления | математика | Britannica". www.britannica.com . Абзац 2, предложение 4. Архивировано из оригинала 2023-08-10 . Получено 2022-11-24 .
4. Тиллингаст-Раби, Эмори. «Система чисел, изобретенная школьниками-инуитами, дебютирует в Кремниевой долине». Scientific American . Архивировано из оригинала 19 июля 2023 г. Получено 24 июля 2023 г.
5. Мэдден, Дэниел Дж.; Обри, Джейсон А. (2017). Введение в доказательство посредством реального анализа. John Wiley & Sons. стр. 3. ISBN 9781119314721.
6. Массер, Гэри Л.; Петерсон, Блейк Э.; Бергер, Уильям Ф. (2013). Математика для учителей начальной школы: современный подход. John Wiley & Sons. стр. 87. ISBN 978-1-118-48700-6.
7. Розен, Кеннет (2013). Дискретная математика и ее приложения. Глобальное издание . McGraw Hill. ISBN 978-0-07-131501-2.См. Приложение I.
8. Hall, FM (1972). Введение в абстрактную алгебру. Cambridge University Press . стр. 171. ISBN 978-0-521-08484-0.
9. Резник, Л. Б.; Форд, В. В. (2012). Психология математики для обучения. Routledge. стр. 110. ISBN 978-1-136-55759-0.
10. "Everyday Mathematics4 at Home". Everyday Mathematics Online . Получено 26 декабря 2022 г.
11. "Алгоритмы вычитания - Кафедра математики в UTSA". mathresearch.utsa.edu . Получено 2024-04-01 .
12. Росс, Сьюзен. «Вычитание в Соединенных Штатах: историческая перспектива» (PDF) . Microsoft Word - Выпуск 2 -9/23/ . Архивировано из оригинала (PDF) 11 августа 2017 г. . Получено 25 июня 2019 г. .
13. Клэппер, Пол (1916). «Преподавание арифметики: руководство для учителей. стр. 177» . Получено 11.03.2016 .
14. Смит, Дэвид Юджин (1913). "Преподавание арифметики. С. 77" . Получено 11.03.2016 .
15. «Дебаты о стиле преподавания математики». edmontonjournal.com .
16. Голлом, Марк (10 апреля 2016 г.). «Преподаватели спорят о том, являются ли некоторые основы математики «мертвой темой в 2016 году».