Проблема логической выполнимости

Проблема определения того, может ли булева формула быть истинной.

В логике и информатике проблема булевой выполнимости (иногда называемая проблемой пропозициональной выполнимости и сокращенно ВЫПОЛНЯЕМОСТЬ , SAT или B-SAT ) — это проблема определения, существует ли интерпретация , удовлетворяющая данной булевой формуле . Другими словами, он спрашивает, могут ли переменные данной логической формулы быть последовательно заменены значениями ИСТИНА или ЛОЖЬ таким образом, чтобы формула имела значение ИСТИНА. В этом случае формула называется выполнимой . С другой стороны, если такого присвоения не существует, функция, выраженная формулой, является ЛОЖНОЙ для всех возможных присвоений переменных, и формула является невыполнимой . Например, формула « a AND NOT b » выполнима, поскольку можно найти значения a  = TRUE и b  = FALSE, которые делают ( a AND NOT b ) = TRUE. Напротив, выражение « А И НЕ а » невыполнимо.

SAT — первая задача, NP-полнота которой была доказана ; см. теорему Кука – Левина . Это означает, что все задачи класса сложности NP , который включает в себя широкий спектр задач естественного решения и оптимизации, в лучшем случае так же сложны для решения, как и SAT. Не существует известного алгоритма, который эффективно решает каждую задачу SAT, и обычно считается, что такого алгоритма не существует; однако это убеждение не было доказано математически, и решение вопроса о том, имеет ли SAT алгоритм с полиномиальным временем, эквивалентно проблеме P и NP , которая является известной открытой проблемой в теории вычислений.

Тем не менее, по состоянию на 2007 год эвристические SAT-алгоритмы способны решать экземпляры задач, включающие десятки тысяч переменных и формулы, состоящие из миллионов символов, ^[1] чего достаточно для многих практических задач SAT, например, в области искусственного интеллекта и проектирования схем. , ^[2] и автоматическое доказательство теорем .

Определения

Формула пропозициональной логики , также называемая логическим выражением , строится из переменных , операторов И ( конъюнкция , также обозначается ∧), ИЛИ ( дизъюнкция , ∨), НЕ ( отрицание , ¬) и круглых скобок. Формула считается выполнимой, если ее можно сделать ИСТИНОЙ путем присвоения ее переменным соответствующих логических значений (т. е. ИСТИНА, ЛОЖЬ). Задача булевой выполнимости (SAT) заключается в том, чтобы по заданной формуле проверить, выполнима ли она. Эта проблема решения имеет центральное значение во многих областях информатики , включая теоретическую информатику , теорию сложности , ^{[3] [4]} алгоритмику , криптографию ^{[5] [6]} и искусственный интеллект . ^{[7] [ необходимы дополнительные ссылки ]}

Конъюнктивная нормальная форма

Литерал — это либо переменная (в этом случае он называется положительным литералом ), либо отрицание переменной (называемое отрицательным литералом ). Предложение — это дизъюнкция литералов (или один литерал). Предложение называется предложением Хорна , если оно содержит не более одного положительного литерала. Формула находится в конъюнктивной нормальной форме (КНФ), если она представляет собой соединение предложений (или одно предложение).

Например, x ₁ — положительный литерал, ¬ x ₂ — отрицательный литерал, x ₁ ∨ ¬ x ₂ — предложение. Формула ( x ₁ ∨ ¬ x ₂ ) ∧ (¬ x ₁ ∨ x ₂ ∨ x ₃ ) ∧ ¬ x ₁ находится в конъюнктивной нормальной форме; его первое и третье предложения являются положениями Хорна, а второе - нет. Формула выполнима, если произвольно выбрать x ₁  = FALSE, x ₂  = FALSE и x ₃ , поскольку (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ x ₃ ) ∧ ¬FALSE дает (FALSE ∨ TRUE) ∧ (ИСТИНА ∨ ЛОЖЬ ∨ x ₃ ) ∧ ИСТИНА и, в свою очередь, к ИСТИНА ∧ ИСТИНА ∧ ИСТИНА (т. е. к ИСТИНА). Напротив, формула КНФ a ∧ ¬ a , состоящая из двух предложений одного литерала, невыполнима, поскольку для a =TRUE или a =FALSE она оценивается как TRUE ∧ ¬TRUE (т. е. FALSE) или FALSE ∧ ¬FALSE (т. е. , снова ЛОЖЬ), соответственно.

Для некоторых версий задачи SAT полезно определить понятие обобщенной формулы конъюнктивной нормальной формы , а именно. как соединение произвольного числа обобщенных предложений , причем последнее имеет форму R ( l ₁ ,..., l _n ) для некоторой булевой функции R и (обычных) литералов l _i . Различные наборы разрешенных логических функций приводят к разным версиям проблемы. Например, R (¬ x , a , b ) является обобщенным предложением, а R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R ( c , d ,¬ z ) является обобщенным предложением. конъюнктивная нормальная форма. Эта формула используется ниже, где R — это тернарный оператор, который имеет значение ИСТИНА только тогда, когда один из его аргументов является истинным.

Используя законы булевой алгебры , каждую формулу логики высказываний можно преобразовать в эквивалентную конъюнктивную нормальную форму, которая, однако, может быть экспоненциально длиннее. Например, преобразование формулы ( x ₁ ∧ y ₁ ) ∨ ( x ₂ ∧ y ₂ ) ∨ ... ∨ ( x _n ∧ y _n ) в конъюнктивную нормальную форму дает

( Икс ₁  ∨  Икс ₂  ∨ … ∨  Икс _п ) ∧

( y ₁  ∨  Икс ₂  ∨ … ∨  Икс _п ) ∧

( Икс ₁  ∨  y ₂  ∨ … ∨  Икс _п ) ∧

( y ₁  ∨  y ₂  ∨ … ∨  Икс _п ) ∧ ... ∧

( Икс ₁  ∨  Икс ₂  ∨ … ∨  y _п ) ∧

( y ₁  ∨  Икс ₂  ∨ … ∨  y _п ) ∧

( Икс ₁  ∨  y ₂  ∨ … ∨  y _п ) ∧

( y ₁  ∨  y ₂  ∨ … ∨  y _п ) ;

в то время как первый представляет собой дизъюнкцию n конъюнкций по 2 переменных, второй состоит из 2 ⁿ предложений по n переменных.

Однако с помощью преобразования Цейтина мы можем найти эквивыполнимую формулу конъюнктивной нормальной формы с длиной, линейной по размеру исходной формулы пропозициональной логики.

Сложность

SAT была первой известной NP-полной задачей, как доказал Стивен Кук из Университета Торонто в 1971 году ^[8] и независимо Леонид Левин из Российской академии наук в 1973 году . ^[9] До этого времени концепция NP-полной проблемы даже не существовало. Доказательство показывает, как любую проблему принятия решения в классе сложности NP можно свести к задаче SAT для формул CNF ^{[примечание 1]} , иногда называемой CNFSAT . Полезным свойством сокращения Кука является то, что оно сохраняет количество принимаемых ответов. Например, еще одна проблема в NP — решить, имеет ли данный граф 3-раскраску ; если граф имеет 17 допустимых трехцветных раскрасок, формула SAT, полученная с помощью сокращения Кука – Левина, будет иметь 17 удовлетворяющих назначений.

NP-полнота относится только к времени выполнения экземпляров наихудшего случая. Многие случаи, возникающие в практических приложениях, можно решить гораздо быстрее. См. Алгоритмы решения SAT ниже.

3-выполнимость

Экземпляр 3-SAT ( x ∨ x ∨ y ) ∧ (¬ x ∨ ¬ y ∨ ¬ y ) ∧ (¬ x ∨ y ∨ y ) сведен к задаче о клике . Зеленые вершины образуют 3-клику и соответствуют удовлетворяющему присваиванию x = FALSE, y = TRUE.

Как и проблема выполнимости произвольных формул, определение выполнимости формулы в конъюнктивной нормальной форме, где каждое предложение ограничено не более чем тремя литералами, также является NP-полным; эта проблема называется 3-SAT , 3CNFSAT или 3-выполнимостью . Чтобы свести неограниченную задачу SAT к 3-SAT, преобразуйте каждое предложение l ₁ ∨ ⋯ ∨ l _n в конъюнкцию из n - 2 предложений .

( л ₁ ∨ л ₂ ∨ Икс ₂ ) ∧

(¬ Икс ₂ ∨ л ₃ ∨ Икс ₃ ) ∧

(¬ Икс ₃ ∨ л ₄ ∨ Икс ₄ ) ∧ ⋯ ∧

(¬ Икс _{п - 3} ∨ л _{п - 2} ∨ Икс _{п - 2} ) ∧

(¬ Икс _{п - 2} ∨ л _{п - 1} ∨ л _п )

где x ₂ , ⋯ ,  x _{n − 2} — свежие переменные, больше нигде не встречающиеся. Хотя эти две формулы логически не эквивалентны , они равновыполнимы . Формула, полученная в результате преобразования всех предложений, имеет длину не более чем в 3 раза, т. е. рост длины является полиномиальным. ^[10]

3-SAT — одна из 21 NP-полной задачи Карпа , и она используется в качестве отправной точки для доказательства того, что другие задачи также являются NP-трудными . ^{[примечание 2]} Это делается путем полиномиального сокращения времени от 3-SAT до другой проблемы. Примером задачи, в которой использовался этот метод, является задача о клике : для формулы CNF, состоящей из c предложений, соответствующий граф состоит из вершины для каждого литерала и ребра между каждыми двумя непротиворечивыми ^{[примечание 3]} литералами . из разных статей, см. картина. Граф имеет c -клику тогда и только тогда, когда формула выполнима. ^[11]

Существует простой рандомизированный алгоритм, предложенный Шёнингом (1999), который работает за время (4/3) ⁿ , где n — количество переменных в предложении 3-SAT, и позволяет с высокой вероятностью правильно решить 3-SAT. ^[12]

Гипотеза экспоненциального времени утверждает, что ни один алгоритм не может решить 3-SAT (или даже k -SAT для любого ) за время exp( o ( n )) (т. е. существенно быстрее, чем экспоненциальное за n ). ${\displaystyle k>2}$

Селман, Митчелл и Левеск (1996) приводят эмпирические данные о сложности случайно сгенерированных формул 3-SAT в зависимости от их параметров размера. Сложность измеряется количеством рекурсивных вызовов, выполняемых алгоритмом DPLL . Они определили область фазового перехода от почти наверняка выполнимых к почти наверняка невыполнимым формулам при соотношении предложений к переменным около 4,26. ^[13]

3-выполнимость можно обобщить до k-выполнимости ( k-SAT , также k-CNF-SAT ), когда формулы в CNF рассматриваются с каждым предложением, содержащим до k литералов. ^{[ нужна цитата ]} Однако, поскольку для любого k ≥ 3 эта задача не может быть ни проще, чем 3-SAT, ни сложнее, чем SAT, а последние два являются NP-полными, поэтому должна быть и k-SAT.

Некоторые авторы ограничивают k-SAT формулами CNF ровно с k литералами . ^{[ нужна ссылка ]} Это также не приводит к другому классу сложности, поскольку каждое предложение l ₁ ∨ ⋯ ∨ l _j с литералами j < k может быть дополнено фиксированными фиктивными переменными до l ₁ ∨ ⋯ ∨ l _j ∨ d _{j + 1} ∨ ⋯ ∨ d _k . После заполнения всех предложений необходимо добавить 2 ^k -1 дополнительных предложений ^{[примечание 4] , чтобы гарантировать, что только} d ₁ = ⋯ = d _k =FALSE может привести к удовлетворительному присваиванию. Поскольку k не зависит от длины формулы, дополнительные предложения приводят к постоянному увеличению длины. По той же причине не имеет значения, разрешены ли в предложениях повторяющиеся литералы , как в ¬ x ∨ ¬ y ∨ ¬ y .

Особые случаи SAT

Конъюнктивная нормальная форма

Конъюнктивная нормальная форма (в частности, с тремя литералами в предложении) часто считается каноническим представлением формул SAT. Как показано выше, общая проблема SAT сводится к 3-SAT, задаче определения выполнимости формул в этой форме.

Дизъюнктивная нормальная форма

SAT тривиален, если формулы ограничены формулами в дизъюнктивной нормальной форме , то есть они представляют собой дизъюнкцию конъюнкций литералов. Такая формула действительно выполнима тогда и только тогда, когда хотя бы одна из ее конъюнкций выполнима, а конъюнкция выполнима тогда и только тогда, когда она не содержит одновременно x и NOT x для некоторой переменной x . Это можно проверить за линейное время. Более того, если они ограничены полной дизъюнктивной нормальной формой , в которой каждая переменная появляется ровно один раз в каждой конъюнкции, их можно проверить за постоянное время (каждая конъюнктура представляет одно удовлетворяющее присваивание). Но для преобразования общей задачи SAT в дизъюнктивную нормальную форму может потребоваться экспоненциальное время и пространство; для примера поменяйте местами «∧» и «∨» в приведенном выше примере экспоненциального разрушения для конъюнктивных нормальных форм.

Ровно-1 3-выполнимость

Слева: сокращение Шефером пункта 3-SAT x ∨ y ∨ z . Результатом R является ИСТИНА (1) , если ровно один из ее аргументов имеет значение ИСТИНА, и ЛОЖЬ (0) в противном случае. Проверяются все 8 комбинаций значений x , y , z , по одному в строке. Новые переменные a ,..., f могут быть выбраны так, чтобы удовлетворять всем условиям (ровно один зеленый аргумент для каждого R ) во всех строках, кроме первой, где x ∨ y ∨ z имеет значение ЛОЖЬ. Справа: более простая редукция с теми же свойствами.

Вариантом проблемы выполнимости 3 является 3-SAT «один из трех» (также известный как «1 из 3-SAT» и «точно 1 3-SAT» ). Учитывая конъюнктивную нормальную форму с тремя литералами в каждом предложении, проблема состоит в том, чтобы определить, существует ли истинное присвоение переменным так, чтобы каждое предложение имело ровно один TRUE литерал (и, следовательно, ровно два FALSE литерала). Напротив, обычный 3-SAT требует, чтобы каждое предложение имело хотя бы один TRUE-литерал. Формально задача 3-SAT «один из трех» задается как обобщенная конъюнктивная нормальная форма со всеми обобщенными предложениями, использующими тернарный оператор R , который имеет значение ИСТИНА только в том случае, если только один из его аргументов является истинным. Когда все литералы формулы 3-SAT «один к трем» положительны, проблема выполнимости называется положительной 3-SAT «один к трем» .

Один из трех 3-SAT вместе с его положительным случаем указан как NP-полная проблема «LO4» в стандартном справочнике Майкла Р. Гари и Дэвида «Компьютеры и трудноразрешимость: руководство по теории NP-полноты» . С. Джонсон . Томас Джером Шефер доказал, что 3-SAT «один из трех» является NP-полным как частный случай теоремы о дихотомии Шефера , которая утверждает, что любая проблема, обобщающая булеву выполнимость определенным образом, находится либо в классе P, либо является NP- полный. ^[14]

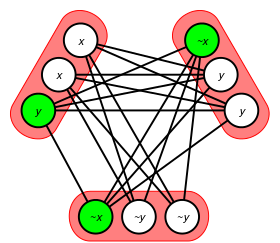
Шефер предлагает конструкцию, позволяющую легко за полиномиальное время сократить 3-SAT до 3-SAT один к трем. Пусть «( x или y или z )» — предложение в формуле 3CNF. Добавьте шесть новых логических переменных a , b , c , d , e и f , которые будут использоваться для моделирования этого предложения, а не другого. Тогда формула R ( x , a , d ) ∧ R ( y , b , d ) ∧ R ( a , b , e ) ∧ R ( c , d , f ) ∧ R ( z , c , FALSE) выполнима по формуле некоторая установка новых переменных тогда и только тогда, когда хотя бы один из x , y или z равен TRUE, см. рисунок (слева). Таким образом, любой экземпляр 3-SAT с m предложений и n переменными может быть преобразован в эквивалентный экземпляр 3-SAT «один из трех» с 5 m предложений и n +6 m переменных. ^[15] Другая редукция включает только четыре новые переменные и три предложения: R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R( c , d , ¬ z ), см. рисунок (справа).

Не все-равная 3-выполнимость

Другой вариант — проблема не-всего равного 3-выполнимости (также называемая NAE3SAT ). Учитывая конъюнктивную нормальную форму с тремя литералами в каждом предложении, проблема состоит в том, чтобы определить, существует ли присвоение переменным такое, что ни в одном предложении все три литерала не имеют одинаковое значение истинности. Эта проблема также является NP-полной, даже если в соответствии с теоремой Шефера о дихотомии не допускаются символы отрицания. ^[14]

Линейный САТ

Формула 3-SAT называется линейной SAT ( LSAT ), если каждое предложение (рассматриваемое как набор литералов) пересекает не более одного другого предложения, и, более того, если два предложения пересекаются, то они имеют ровно один общий литерал. Формулу LSAT можно изобразить как набор непересекающихся полузамкнутых интервалов на линии. Решение о выполнимости формулы LSAT является NP-полным. ^[16]

2-выполнимость

SAT проще, если количество литералов в предложении ограничено максимум двумя, и в этом случае проблема называется 2-SAT . Эта задача может быть решена за полиномиальное время и фактически является полной для класса сложности NL . Если дополнительно все операции ИЛИ в литералах заменяются операциями XOR , результат называется исключающей или 2-выполнимостью , что является полной задачей для класса сложности SL = L.

Хорн-выполнимость

Проблема определения выполнимости данного соединения предложений Хорна называется Хорн-выполнимостью , или HORN-SAT . Ее можно решить за полиномиальное время с помощью одного шага алгоритма распространения единиц , который создает единственную минимальную модель набора предложений Хорна (относительно набора литералов, которым присвоено значение TRUE). Хорн-выполнимость P-полна . Ее можно рассматривать как версию проблемы булевой выполнимости, предложенную P. Кроме того, определение истинности количественных формул Хорна может быть выполнено за полиномиальное время. ^[17]

Предложения Хорна представляют интерес, поскольку они способны выражать импликацию одной переменной из набора других переменных. Действительно, одно такое предложение ¬ x ₁ ∨ ... ∨ ¬ x _n ∨ y можно переписать как x ₁ ∧ ... ∧ x _n → y , то есть, если все x ₁ ,..., x _n ИСТИННЫ. , то y также должно быть TRUE.

Обобщением класса формул Хорна являются формулы переименовываемого Хорна, которые представляют собой набор формул, которые можно поместить в форму Хорна путем замены некоторых переменных их соответствующим отрицанием. Например, ( x ₁ ∨ ¬ x ₂ ) ∧ (¬ x ₁ ∨ x ₂ ∨ x ₃ ) ∧ ¬ x ₁ не является формулой Хорна, но может быть переименовано в формулу Хорна ( x ₁ ∨ ¬ x ₂ ) ∧ (¬ x ₁ ∨ x ₂ ∨ ¬ y ₃ ) ∧ ¬ x ₁ путем введения y ₃ как отрицания x ₃ . Напротив, никакое переименование ( x ₁ ∨ ¬ x ₂ ∨ ¬ x ₃ ) ∧ (¬ x ₁ ∨ x ₂ ∨ x ₃ ) ∧ ¬ x ₁ не приводит к формуле Хорна. Проверку существования такой замены можно произвести за линейное время; следовательно, выполнимость таких формул находится в P, поскольку ее можно решить, сначала выполнив эту замену, а затем проверив выполнимость полученной формулы Хорна.

XOR-выполнимость

Другим особым случаем является класс задач, где каждое предложение содержит операторы XOR (т. е. исключающее или ), а не (простые) операторы OR. ^{[примечание 5]} Это в P , поскольку формулу XOR-SAT также можно рассматривать как систему линейных уравнений по модулю 2 и можно решать за кубическое время методом исключения Гаусса ; ^[18] см. пример в рамке. Эта переработка основана на родстве между булевыми алгебрами и булевыми кольцами , а также на том факте, что арифметика по модулю два образует конечное поле . Поскольку XOR b XOR c оценивается как TRUE тогда и только тогда, когда ровно 1 или 3 члена { a , b , c } имеют значение TRUE , каждое решение задачи 1-в-3-SAT для данной формулы CNF также является решением задачи XOR-3-SAT, а каждое решение XOR-3-SAT, в свою очередь, является решением задачи 3-SAT, ср. картина. Как следствие, для каждой формулы CNF можно решить проблему XOR-3-SAT, определенную формулой, и на основе результата сделать вывод, что проблема 3-SAT разрешима, или что проблема 1-в-3- Проблема SAT неразрешима.

При условии, что классы сложности P и NP не равны , ни 2-, ни Horn-, ни XOR-выполнимость не является NP-полной, в отличие от SAT.

Теорема Шефера о дихотомии

Вышеуказанные ограничения (CNF, 2CNF, 3CNF, Horn, XOR-SAT) принудили рассматриваемые формулы быть конъюнкциями подформул; каждое ограничение устанавливает определенную форму для всех подформул: например, только бинарные предложения могут быть подформулами в 2CNF.

Теорема о дихотомии Шефера утверждает, что для любого ограничения на булевы функции, которые можно использовать для формирования этих подформул, соответствующая проблема выполнимости является P или NP-полной. Принадлежность P выполнимости формул 2CNF, Horn и XOR-SAT является частным случаем этой теоремы. ^[14]

В следующей таблице приведены некоторые распространенные варианты SAT.

Расширения SAT

Расширение, получившее значительную популярность с 2003 года, — это теории выполнимости по модулю ( SMT ), которые могут обогащать формулы CNF линейными ограничениями, массивами, совершенно разными ограничениями, неинтерпретируемыми функциями , ^[19] и т. д . Такие расширения обычно остаются NP-полными, но очень Теперь доступны эффективные решатели, которые могут обрабатывать многие виды ограничений.

Проблема выполнимости становится более сложной, если кванторам «для всех» ( ∀ ) и «существует» ( ∃ ) разрешено связывать логические переменные. Примером такого выражения может быть ∀ x ∀ y ∃ z ( x ∨ y ∨ z ) ∧ (¬ x ∨ ¬ y ∨ ¬ z ) ; это действительно так, поскольку для всех значений x и y можно найти подходящее значение z , а именно. z = ИСТИНА, если и x , и y имеют значение ЛОЖЬ, и z = ЛОЖЬ в противном случае. Сам SAT (молчаливо) использует только ∃-кванторы. Если вместо этого разрешены только кванторы ∀, получается так называемая проблема тавтологии , которая является ко-NP-полной . Если разрешены оба квантора, проблема называется проблемой количественной булевой формулы ( QBF ), которая, как можно показать, является PSPACE-полной . Широко распространено мнение, что задачи, полные по PSPACE, строго сложнее, чем любая задача в NP, хотя это еще не доказано. Используя высокопараллельные P-системы , проблемы QBF-SAT можно решать за линейное время. ^[20]

Обычный SAT спрашивает, есть ли хотя бы одно присвоение переменной, которое делает формулу истинной. Разнообразие вариантов касается количества таких заданий:

• MAJ-SAT спрашивает, соответствует ли формула ИСТИНЕ в большинстве всех заданий. Известно, что он полон для PP — вероятностного класса.
• #SAT , проблема подсчета того, сколько назначений переменных удовлетворяет формуле, является проблемой подсчета, а не проблемой решения, и является #P-полной .
• UNIQUE SAT ^[21] — это задача определения того, имеет ли формула ровно одно присвоение. Это полный для США ^[22] класс сложности , описывающий проблемы, решаемые с помощью недетерминированной машины Тьюринга с полиномиальным временем , которая принимает, когда существует ровно один недетерминированный принимающий путь, и отклоняет в противном случае.
• UNAMBIGUOUS-SAT — это название проблемы выполнимости, когда входные данные ограничены формулами, имеющими не более одного удовлетворяющего назначения. Проблема также называется USAT . ^[23] Алгоритму решения UNAMBIGUOUS-SAT разрешено демонстрировать любое поведение, включая бесконечный цикл, в формуле, имеющей несколько удовлетворяющих заданий. Хотя эта проблема кажется более простой, Валиант и Вазирани показали [ ^24] , что если существует практический (т.е. рандомизированный полиномиальный ) алгоритм для ее решения, то все проблемы в NP могут быть решены так же легко.
• MAX-SAT , проблема максимальной выполнимости , является FNP- обобщением SAT. Он требует максимального количества пунктов, которое может быть удовлетворено любым заданием. Он имеет эффективные алгоритмы аппроксимации , но его NP-трудно решить точно. Хуже того, она является APX -полной, что означает, что для этой задачи не существует схемы аппроксимации с полиномиальным временем (PTAS), если только P = NP.
• WMSAT — это проблема поиска присвоения минимального веса, удовлетворяющего монотонной булевой формуле (т. е. формуле без какого-либо отрицания). Веса пропозициональных переменных задаются на входе задачи. Вес присваивания — это сумма весов истинных переменных. Эта задача NP-полна (см. теорему 1 из ^[25] ).

Другие обобщения включают выполнимость для логики первого и второго порядка , задачи удовлетворения ограничений , целочисленное программирование 0-1 .

Находим удовлетворяющее задание

В то время как SAT является проблемой решения , проблема поиска удовлетворяющего задания сводится к SAT. То есть каждый алгоритм, который правильно отвечает, разрешима ли задача SAT, может быть использован для поиска удовлетворяющего задания. Сначала задается вопрос по данной формуле Φ. Если ответ «нет», формула невыполнима. В противном случае вопрос задается по частично конкретизированной формуле Φ { x ₁ =TRUE} , т.е. Φ с первой переменной x ₁ , замененной на TRUE и упрощенной соответственно. Если ответ «да», то x ₁ =ИСТИНА, в противном случае x ₁ =ЛОЖЬ. Значения остальных переменных можно найти впоследствии таким же образом. Всего требуется n +1 запуск алгоритма, где n — количество различных переменных в Φ.

Это свойство используется в нескольких теоремах теории сложности:

NP ⊆ P/poly ⇒ PH = Σ 2   ( теорема Карпа–Липтона )

НП ⊆ БПП ⇒ НП = РП

P = NP ⇒ FP = FNP

Алгоритмы решения САТ

Поскольку задача SAT является NP-полной, для нее известны только алгоритмы с экспоненциальной сложностью в худшем случае. Несмотря на это, эффективные и масштабируемые алгоритмы для SAT были разработаны в 2000-х годах и способствовали значительному прогрессу в нашей способности автоматически решать примеры задач, включающие десятки тысяч переменных и миллионы ограничений (т.е. предложений). ^[1] Примеры таких проблем в автоматизации электронного проектирования (EDA) включают формальную проверку эквивалентности , проверку модели , формальную проверку конвейерных микропроцессоров , ^[19] автоматическую генерацию тестовых шаблонов , маршрутизацию FPGA , ^[26] планирование и задачи планирования , и скоро. Механизм решения SAT также считается важным компонентом в наборе инструментов автоматизации проектирования электроники .

Основные методы, используемые современными решателями SAT, включают алгоритм Дэвиса-Патнэма-Логеманна-Лавленда (или DPLL), обучение предложений, управляемое конфликтами (CDCL), и алгоритмы стохастического локального поиска, такие как WalkSAT . Почти все решатели SAT имеют тайм-ауты, поэтому они завершатся в разумные сроки, даже если не смогут найти решение. Разные решатели SAT найдут разные случаи легкими или трудными, и некоторые преуспевают в доказательстве невыполнимости, а другие в поиске решений. Недавние попытки были предприняты для изучения выполнимости экземпляра с использованием методов глубокого обучения. ^[27]

Решатели SAT разрабатываются и сравниваются в конкурсах по решению SAT. ^[28] Современные решатели SAT также оказывают значительное влияние на области верификации программного обеспечения, решения ограничений в искусственном интеллекте и исследования операций, среди прочего.

Смотрите также

• Неудовлетворительное ядро
• Теории выполнимости по модулю
• Подсчет САТ
• Планарный САТ
• Алгоритм Карлоффа – Цвика
• Выполнимость схемы

Примечания

1. Проблема SAT для произвольных формул также является NP-полной, поскольку легко показать, что она находится в NP, и она не может быть проще, чем SAT для формул CNF.
2. то есть, по крайней мере, так же сложно, как и любая другая задача в NP. Задача решения является NP-полной тогда и только тогда, когда она находится в NP и является NP-трудной.
3. т.е. такой, что один литерал не является отрицанием другого
4. а именно. все макстермы , которые можно построить с помощью d ₁ ,⋯, d _k , кроме d ₁ ∨⋯∨ d _k
5. Формально используются обобщенные конъюнктивные нормальные формы с троичной булевой функцией R , которая ИСТИНА только в том случае, если 1 или 3 ее аргумента являются истинными. Входное предложение с более чем 3 литералами может быть преобразовано в равновыполнимое соединение предложений с 3 литералами, аналогичное приведенному выше; т.е. XOR-SAT можно свести к XOR-3-SAT.

Внешние ссылки

• SAT Game: попробуйте самостоятельно решить задачу о логической выполнимости
• Сайт международного конкурса SAT
• Международная конференция по теории и приложениям проверки выполнимости
• Журнал по выполнимости, логическому моделированию и вычислениям
• SAT Live, совокупный веб-сайт для исследований проблемы выполнимости
• Ежегодная оценка решателей MaxSAT

Рекомендации

1. Охрименко, Ольга; Стаки, Питер Дж.; Кодиш, Майкл (2007), «Распространение = ленивая генерация предложений», Принципы и практика программирования с ограничениями – CP 2007 , Конспекты лекций по информатике, том. 4741, стр. 544–558, CiteSeerX  10.1.1.70.5471 , doi : 10.1007/978-3-540-74970-7_39, современные решатели SAT часто могут решать задачи с миллионами ограничений и сотнями тысяч переменных..
2. Хонг, Тед; Ли, Яньцзин; Пак, Сунг-Бём; Муи, Диана; Лин, Дэвид; Калек, Зияд Абдель; Хаким, Нагиб; Наэйми, Хелия; Гарднер, Дональд С.; Митра, Субхасиш (ноябрь 2010 г.). «QED: тесты быстрого обнаружения ошибок для эффективной пост-кремниевой проверки». Международная конференция по тестированию IEEE 2010 . стр. 1–10. дои : 10.1109/TEST.2010.5699215. ISBN 978-1-4244-7206-2. S2CID  7909084.
3. Карп, Ричард М. (1972). «Сводимость среди комбинаторных задач» (PDF) . У Раймонда Э. Миллера; Джеймс В. Тэтчер (ред.). Сложность компьютерных вычислений . Нью-Йорк: Пленум. стр. 85–103. ISBN 0-306-30707-3. Архивировано из оригинала (PDF) 29 июня 2011 г. Проверено 7 мая 2020 г.Здесь: стр.86
4. Ахо, Альфред В.; Хопкрофт, Джон Э.; Уллман, Джеффри Д. (1974). Проектирование и анализ компьютерных алгоритмов . Аддисон-Уэсли. п. 403. ИСБН 0-201-00029-6.
5. Массаччи, Фабио; Марраро, Лаура (1 февраля 2000 г.). «Логический криптоанализ как проблема SAT». Журнал автоматизированного рассуждения . 24 (1): 165–203. дои : 10.1023/А: 1006326723002. S2CID  3114247.
6. Миронов, Илья; Чжан, Линтао (2006). «Применение решателей SAT для криптоанализа хэш-функций». В Бьере, Армин; Гомес, Карла П. (ред.). Теория и приложения тестирования выполнимости - SAT 2006 . Конспекты лекций по информатике. Том. 4121. Спрингер. стр. 102–115. дои : 10.1007/11814948_13. ISBN 978-3-540-37207-3.
7. Визель, Ю.; Вайсенбахер, Г.; Малик, С. (2015). «Решатели логической выполнимости и их применение при проверке моделей». Труды IEEE . 103 (11): 2021–2035. дои : 10.1109/JPROC.2015.2455034. S2CID  10190144.
8. Кук, Стивен А. (1971). «Сложность процедур доказательства теорем» (PDF) . Материалы третьего ежегодного симпозиума ACM по теории вычислений - STOC '71 . стр. 151–158. CiteSeerX 10.1.1.406.395 . дои : 10.1145/800157.805047. S2CID  7573663. Архивировано (PDF) из оригинала 9 октября 2022 г. 
9. Левин, Леонид (1973). «Универсальные задачи поиска». Проблемы передачи информации . 9 (3): 115–116.(pdf) (на русском языке) , перевод на английский язык Трахтенбротом, бакалавром (1984). «Обзор российских подходов к алгоритмам перебора» . Анналы истории вычислительной техники . 6 (4): 384–400. дои : 10.1109/MAHC.1984.10036. S2CID  950581.
10. Ахо, Хопкрофт и Ульман (1974), Теорема 10.4.
11. Ахо, Хопкрофт и Ульман (1974), Теорема 10.5.
12. Шёнинг, Уве (октябрь 1999 г.). «Вероятностный алгоритм для решения задач k-SAT и удовлетворения ограничений» (PDF) . 40-й ежегодный симпозиум по основам информатики (кат. № 99CB37039) . стр. 410–414. дои : 10.1109/SFCS.1999.814612. ISBN 0-7695-0409-4. S2CID  123177576. Архивировано (PDF) из оригинала 9 октября 2022 г.
13. Селман, Барт; Митчелл, Дэвид; Левеск, Гектор (1996). «Построение задач жесткой выполнимости». Искусственный интеллект . 81 (1–2): 17–29. CiteSeerX 10.1.1.37.7362 . дои : 10.1016/0004-3702(95)00045-3. 
14. Шефер, Томас Дж. (1978). «Сложность задач выполнимости» (PDF) . Материалы 10-го ежегодного симпозиума ACM по теории вычислений . Сан-Диего, Калифорния. стр. 216–226. CiteSeerX 10.1.1.393.8951 . дои : 10.1145/800133.804350. 
15. Шефер (1978), с. 222, Лемма 3.5.
16. Аркин, Эстер М.; Баник, Аритра; Карми, Пас; Цитовский, Ги; Кац, Мэтью Дж.; Митчелл, Джозеф С.Б.; Симаков, Марина (11 декабря 2018 г.). «Выделение и закрытие цветных точек». Дискретная прикладная математика . 250 : 75–86. дои : 10.1016/j.dam.2018.05.011 . ISSN  0166-218X.
17. Бунинг, Гонконг; Карпински, Марек; Флогель, А. (1995). «Разрешение для количественных логических формул». Информация и вычисления . Эльзевир. 117 (1): 12–18. дои : 10.1006/inco.1995.1025 .
18. Мур, Кристофер ; Мертенс, Стефан (2011), Природа вычислений, Oxford University Press, стр. 366, ISBN 9780199233212.
19. Р.Э. Брайант, С.М. Герман и М.Н. Велев, Проверка микропроцессора с использованием эффективных процедур принятия решений для логики равенства с неинтерпретируемыми функциями, в аналитических таблицах и родственных методах, стр. 1–13, 1999.
20. Алхазов, Артём; Мартин-Виде, Карлос; Пан, Линьцян (2003). «Решение PSPACE-полной задачи путем распознавания P-систем с ограниченными активными мембранами». Фундамента информатики . 58 : 67–77.Здесь: Раздел 3, Тема 3.1.
21. Бласс, Андреас; Гуревич, Юрий (01.10.1982). «Об единственной проблеме выполнимости». Информация и контроль . 55 (1): 80–88. дои : 10.1016/S0019-9958(82)90439-9 . hdl : 2027.42/23842 . ISSN  0019-9958.
22. "Зоопарк сложности: U - Зоопарк сложности" . сложностьzoo.uwaterloo.ca . Архивировано из оригинала 9 июля 2019 г. Проверено 5 декабря 2019 г.
23. Козен, Декстер С. (2006). «Дополнительная лекция F: Уникальная выполнимость». Теория вычислений . Тексты по информатике. Спрингер. п. 180. ИСБН 9781846282973.
24. Валиант, Л.; Вазирани, В. (1986). «NP — это так же просто, как найти уникальные решения» (PDF) . Теоретическая информатика . 47 : 85–93. дои : 10.1016/0304-3975(86)90135-0 .
25. Булдас, Ахто; Ленин, Александр; Уиллемсон, Ян; Чарнаморд, Антон (2017). «Простые сертификаты невыполнимости деревьев атак». В Обане Сатоши; Чида, Кодзи (ред.). Достижения в области информационной и компьютерной безопасности . Конспекты лекций по информатике. Том. 10418. Международное издательство Springer. стр. 39–55. дои : 10.1007/978-3-319-64200-0_3. ISBN 9783319642000.
26. Ги-Джун Нам; Сакалла, штат Калифорния; Рутенбар, РА (2002). «Новый подход к детальной маршрутизации FPGA посредством логической выполнимости на основе поиска» (PDF) . Транзакции IEEE по автоматизированному проектированию интегральных схем и систем . 21 (6): 674. doi :10.1109/TCAD.2002.1004311. Архивировано из оригинала (PDF) 15 марта 2016 г. Проверено 4 сентября 2015 г.
27. Селсам, Дэниел; Ламм, Мэтью; Бюнц, Бенедикт; Лян, Перси; де Моура, Леонардо; Дилл, Дэвид Л. (11 марта 2019 г.). «Изучение решателя SAT с помощью однобитового наблюдения». arXiv : 1802.03685 [cs.AI].
28. "Веб-страница международных соревнований SAT" . Проверено 15 ноября 2007 г.

Источники

• В эту статью включены материалы с https://web.archive.org/web/20070708233347/http://www.sigda.org/newsletter/2006/eNews_061201.html профессора Карема А. Сакаллы .

дальнейшее чтение

(по дате публикации)

• Гэри, Майкл Р .; Джонсон, Дэвид С. (1979). Компьютеры и трудноразрешимые: Руководство по теории NP-полноты. У. Х. Фриман. стр. A9.1: LO1–LO7, стр. 259–260. ISBN 0-7167-1045-5.
• Маркес-Сильва, Ж.; Гласс, Т. (1999). «Проверка комбинационной эквивалентности с использованием выполнимости и рекурсивного обучения». Конференция и выставка «Проектирование, автоматизация и испытания в Европе», 1999 г. Материалы (кат. № PR00078) (PDF) . п. 145. дои :10.1109/ДАТА.1999.761110. ISBN 0-7695-0078-1. Архивировано (PDF) из оригинала 9 октября 2022 г.
• Кларк, Э.; Бьер, А.; Рэйми, Р.; Чжу, Ю. (2001). «Проверка ограниченной модели с использованием решения выполнимости». Формальные методы проектирования систем . 19 :7–34. дои : 10.1023/А: 1011276507260. S2CID  2484208.
• Джунчилья, Э.; Такчелла, А. (2004). Джунчилья, Энрико; Такчелла, Армандо (ред.). Теория и приложения проверки выполнимости . Конспекты лекций по информатике. Том. 2919. дои : 10.1007/b95238. ISBN 978-3-540-20851-8. S2CID  31129008.
• Бабич, Д.; Бингэм, Дж.; Ху, Эй Джей (2006). «B-Cubing: новые возможности для эффективного решения SAT» (PDF) . Транзакции IEEE на компьютерах . 55 (11): 1315. doi :10.1109/TC.2006.175. S2CID  14819050.
• Родригес, К.; Вильягра, М.; Баран, Б. (2007). «Асинхронные групповые алгоритмы для логической выполнимости» (PDF) . 2007 2-я Биомодели сетевых, информационных и вычислительных систем . стр. 66–69. doi :10.1109/BIMNICS.2007.4610083. S2CID  15185219.
• Гомес, Карла П .; Каутц, Генри; Сабхарвал, Ашиш; Селман, Барт (2008). «Решатели выполнимости». В Хармелене, Фрэнк Ван; Лифшиц, Владимир; Портер, Брюс (ред.). Справочник по представлению знаний . Основы искусственного интеллекта. Том. 3. Эльзевир. стр. 89–134. дои : 10.1016/S1574-6526(07)03002-7. ISBN 978-0-444-52211-5.
• Визель, Ю.; Вайсенбахер, Г.; Малик, С. (2015). «Решатели логической выполнимости и их применение при проверке моделей». Труды IEEE . 103 (11): 2021–2035. дои : 10.1109/JPROC.2015.2455034. S2CID  10190144.
• Кнут, Дональд Э. (2022). «Глава 7.2.2.2: Выполняемость». Искусство компьютерного программирования . Том. 4B: Комбинаторные алгоритмы, часть 2. Addison-Wesley Professional. стр. 185–369. ISBN 978-0-201-03806-4.