Гомоскедастичность и гетероскедастичность

Статистическая собственность

График со случайными данными, показывающий гомоскедастичность: при каждом значении x значение y точек имеет примерно одинаковую дисперсию .

График со случайными данными, показывающий гетероскедастичность: дисперсия значений y точек увеличивается с ростом значений x .

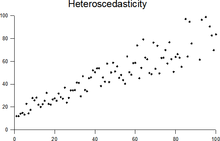
В статистике последовательность случайных величин называется гомоскедастичной ( / ˌ h oʊ m oʊ s k ə ˈ d æ s t ɪ k / ) , если все ее случайные величины имеют одинаковую конечную дисперсию ; это также известно как однородность дисперсии . Дополнительное понятие называется гетероскедастичностью , также известной как неоднородность дисперсии . Также часто используются написания homos k edasticity и heteros k edasticity . «Скедастичность» происходит от древнегреческого слова «skedánnymi», что означает «рассеивать». ^{[1] [2] [3]} Предположение, что переменная является гомоскедастической, когда на самом деле она гетероскедастическая ( / ˌ h ɛ t ər oʊ s k ə ˈ d æ s t ɪ k / ), приводит к несмещенным , но неэффективным точечным оценкам и смещенным оценкам стандартных ошибок , а также может привести к переоценке качества подгонки , измеряемой коэффициентом Пирсона .

Существование гетероскедастичности является серьезной проблемой в регрессионном анализе и дисперсионном анализе , поскольку оно делает недействительными статистические тесты значимости , которые предполагают, что все ошибки моделирования имеют одинаковую дисперсию. Хотя обычная оценка наименьших квадратов все еще является несмещенной при наличии гетероскедастичности, она неэффективна, а вывод, основанный на предположении о гомоскедастичности, вводит в заблуждение. В этом случае в прошлом часто использовался обобщенный метод наименьших квадратов (GLS). ^{[4] [5]} В настоящее время стандартной практикой в ​​эконометрике является включение согласованных с гетероскедастичностью стандартных ошибок вместо использования GLS, поскольку GLS может демонстрировать сильное смещение в небольших выборках, если фактическая скедастичная функция неизвестна. ^[6]

Поскольку гетероскедастичность касается ожиданий второго момента ошибок, ее наличие называется ошибкой спецификации второго порядка. ^[7]

Эконометрист Роберт Энгл был удостоен Нобелевской премии по экономике 2003 года за свои исследования регрессионного анализа в присутствии гетероскедастичности, которые привели к формулировке им метода моделирования авторегрессионной условной гетероскедастичности (ARCH). ^[8]

Определение

Рассмотрим уравнение линейной регрессии , где зависимая случайная величина равна детерминированной переменной , умноженной на коэффициент, плюс случайный член возмущения , который имеет нулевое среднее значение. Возмущения являются гомоскедастическими, если дисперсия является константой ; в противном случае они являются гетероскедастическими. В частности, возмущения являются гетероскедастическими, если дисперсия зависит от или от значения . Один из способов, которым они могут быть гетероскедастическими, — это если (пример скедастической функции ), поэтому дисперсия пропорциональна значению . ${\displaystyle y_{i}=x_{i}\beta _{i}+\varepsilon _{i},\ i=1,\ldots ,N,}$ ${\displaystyle y_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle \beta _{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle x_{i}}$ ${\displaystyle \sigma _{i}^{2}=x_{i}\sigma ^{2}}$ ${\displaystyle x}$

В более общем случае, если матрица дисперсии-ковариации возмущения по имеет непостоянную диагональ, возмущение является гетероскедастическим. ^[9] Матрицы ниже являются ковариациями, когда есть всего три наблюдения во времени. Возмущение в матрице A является гомоскедастическим; это простой случай, когда OLS является лучшей линейной несмещенной оценкой. Возмущения в матрицах B и C являются гетероскедастическими. В матрице B дисперсия является переменной во времени, постоянно увеличиваясь со временем; в матрице C дисперсия зависит от значения . Возмущение в матрице D является гомоскедастическим, поскольку диагональные дисперсии постоянны, даже несмотря на то, что недиагональные ковариации не равны нулю, а обычный метод наименьших квадратов неэффективен по другой причине: последовательная корреляция. ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle x}$

${\displaystyle {\begin{aligned}A&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}}&B&=\sigma ^{2}{\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\\\end{bmatrix}}&C&=\sigma ^{2}{\begin{bmatrix}x_{1}&0&0\\0&x_{2}&0\\0&0&x_{3}\\\end{bmatrix}}&D&=\sigma ^{2}{\begin{bmatrix}1&\rho &\rho ^{2}\\\rho &1&\rho \\\rho ^{2}&\rho &1\\\end{bmatrix}}\end{aligned}}}$

Примеры

Гетероскедастичность часто возникает, когда существует большая разница между размерами наблюдений.

Классический пример гетероскедастичности — доход против расходов на еду. Богатый человек может иногда есть недорогую еду, а иногда — дорогую. Бедный человек почти всегда будет есть недорогую еду. Поэтому люди с более высокими доходами демонстрируют большую изменчивость в расходах на еду.

При запуске ракеты наблюдатель измеряет расстояние, пройденное ракетой, один раз в секунду. В первые пару секунд измерения могут быть точными до ближайшего сантиметра. Через пять минут точность измерений может быть хорошей только до 100 м из-за увеличенного расстояния, атмосферных искажений и множества других факторов. Поэтому измерения расстояния могут демонстрировать гетероскедастичность.

Последствия

Одно из предположений классической линейной регрессионной модели заключается в том, что гетероскедастичности нет. Нарушение этого предположения означает, что теорема Гаусса-Маркова неприменима, а это означает, что оценщики OLS не являются наилучшими линейными несмещенными оценщиками (BLUE) , а их дисперсия не является самой низкой из всех других несмещенных оценщиков. Гетероскедастичность не приводит к смещению оценок коэффициентов по методу наименьших квадратов, хотя она может привести к смещению оценок дисперсии (и, таким образом, стандартных ошибок) коэффициентов по методу наименьших квадратов, возможно, выше или ниже истинной дисперсии популяции. Таким образом, регрессионный анализ с использованием гетероскедастичных данных по-прежнему будет предоставлять несмещенную оценку для связи между предикторной переменной и результатом, но стандартные ошибки и, следовательно, выводы, полученные из анализа данных, являются подозрительными. Смещенные стандартные ошибки приводят к смещению вывода, поэтому результаты проверки гипотез, возможно, неверны. Например, если метод наименьших квадратов выполняется на гетероскедастичном наборе данных, что приводит к смещенной оценке стандартной ошибки, исследователь может не отвергнуть нулевую гипотезу на заданном уровне значимости , когда эта нулевая гипотеза на самом деле нехарактерна для фактической популяции (что приводит к ошибке II типа ).

При определенных предположениях оценщик OLS имеет нормальное асимптотическое распределение при правильной нормализации и центрировании (даже когда данные не исходят из нормального распределения ). Этот результат используется для обоснования использования нормального распределения или распределения хи-квадрат (в зависимости от того, как вычисляется статистика теста ) при проведении проверки гипотезы . Это справедливо даже при гетероскедастичности. Точнее, оценщик OLS при наличии гетероскедастичности асимптотически нормален при правильной нормализации и центрировании с матрицей дисперсии-ковариации , которая отличается от случая гомоскедастичности. В 1980 году Уайт предложил последовательную оценку для матрицы дисперсии-ковариации асимптотического распределения оценщика OLS. ^[2] Это подтверждает использование проверки гипотез с использованием оценщиков OLS и оценщика дисперсии-ковариации Уайта при гетероскедастичности.

Гетероскедастичность также является серьезной практической проблемой, с которой сталкиваются при решении задач дисперсионного анализа . ^[10] F -тест все еще может использоваться в некоторых обстоятельствах. ^[11]

Однако было сказано, что студенты, изучающие эконометрику, не должны слишком остро реагировать на гетероскедастичность. ^[3] Один автор написал: «Неравная дисперсия ошибок имеет смысл корректировать только тогда, когда проблема серьезная». ^[12] Кроме того, еще одно предостережение было в форме: «Гетероскедастичность никогда не была причиной для отказа от хорошей модели». ^{[3] [13]} С появлением гетероскедастичных стандартных ошибок , позволяющих делать выводы без указания условного второго момента ошибки, проверка условной гомоскедастичности не так важна, как в прошлом. ^[6]

Однако для любой нелинейной модели (например, моделей Logit и Probit ) гетероскедастичность имеет более серьезные последствия: оценки максимального правдоподобия (MLE) параметров обычно будут смещенными, а также непоследовательными (если только функция правдоподобия не изменена для правильного учета точной формы гетероскедастичности или распределение не является членом линейного экспоненциального семейства , а функция условного ожидания не указана правильно). ^{[14] [15]} Тем не менее, в контексте моделей бинарного выбора ( Logit или Probit ) гетероскедастичность приведет только к положительному эффекту масштабирования на асимптотическом среднем значении неправильно указанной MLE (т. е. модели, которая игнорирует гетероскедастичность). ^[16] В результате прогнозы, основанные на неправильно указанной MLE, останутся правильными. Кроме того, неправильно указанные Probit и Logit MLE будут асимптотически нормально распределены, что позволяет выполнять обычные тесты значимости (с соответствующей матрицей дисперсии-ковариации). Однако, что касается общей проверки гипотез, как отметил Грин , «простое вычисление надежной ковариационной матрицы для в противном случае непоследовательной оценки не дает ей искупления. Следовательно, достоинство надежной ковариационной матрицы в этой ситуации неясно». ^[17]

Исправление

Существует несколько распространенных поправок на гетероскедастичность. Они следующие:

• Стабилизирующее преобразование данных, например логарифмированных данных. Нелогарифмированные ряды, растущие экспоненциально, часто, по-видимому, имеют увеличивающуюся изменчивость по мере того, как ряд растет с течением времени. Однако изменчивость в процентном отношении может быть довольно стабильной.
• Используйте другую спецификацию для модели (другие переменные X или, возможно, нелинейные преобразования переменных X ).
• Применить метод оценки взвешенных наименьших квадратов , в котором МНК применяется к преобразованным или взвешенным значениям X и Y. Веса изменяются в зависимости от наблюдений, обычно в зависимости от изменяющихся дисперсий ошибок. В одном варианте веса напрямую связаны с величиной зависимой переменной, и это соответствует процентной регрессии наименьших квадратов. ^[18]
• Гетероскедастичные-согласованные стандартные ошибки (HCSE), хотя и смещены, улучшают оценки OLS. ^[2] HCSE является согласованным оценщиком стандартных ошибок в регрессионных моделях с гетероскедастичностью. Этот метод исправляет гетероскедастичность, не изменяя значения коэффициентов. Этот метод может превосходить обычный OLS, поскольку при наличии гетероскедастичности он исправляет ее, однако, если данные гомоскедастичны, стандартные ошибки эквивалентны обычным стандартным ошибкам, оцененным с помощью OLS. Было предложено несколько модификаций метода Уайта для вычисления гетероскедастичных-согласованных стандартных ошибок в качестве поправок с превосходными свойствами конечной выборки.
• Дикий бутстраппинг может использоваться как метод повторной выборки , который учитывает различия в условной дисперсии члена ошибки. Альтернативой является повторная выборка наблюдений вместо ошибок. Обратите внимание, что ошибки повторной выборки без учета связанных значений наблюдения усиливают гомоскедастичность и, таким образом, приводят к неверному выводу.
• Используйте MINQUE или даже обычные оценщики (для независимых выборок с наблюдениями каждая), потери эффективности которых незначительны, когда число наблюдений на выборку велико ( ), особенно для небольшого числа независимых выборок. ^[19] ${\textstyle s_{i}^{2}=(n_{i}-1)^{-1}\sum _{j}\left(y_{ij}-{\bar {y}}_{i}\right)^{2}}$ ${\displaystyle i=1,2,...,k}$ ${\displaystyle j=1,2,...,n_{i}}$ ${\displaystyle n_{i}>5}$

Тестирование

Абсолютное значение остатков для моделированных гетероскедастических данных первого порядка

Остатки можно проверить на гомоскедастичность с помощью теста Бреуша–Пагана ^[20] , который выполняет вспомогательную регрессию квадратов остатков на независимых переменных. Из этой вспомогательной регрессии сохраняется объясненная сумма квадратов, делится на два и затем становится тестовой статистикой для распределения хи-квадрат со степенями свободы, равными числу независимых переменных. ^[21] Нулевая гипотеза этого теста хи-квадрат — гомоскедастичность, а альтернативная гипотеза будет указывать на гетероскедастичность. Поскольку тест Бреуша–Пагана чувствителен к отклонениям от нормальности или малым размерам выборки, вместо него обычно используется тест Кенкера–Бассета или «обобщенный тест Бреуша–Пагана». ^{[22] [ необходимы дополнительные ссылки ]} Из вспомогательной регрессии сохраняется значение R-квадрат, которое затем умножается на размер выборки, а затем становится тестовой статистикой для распределения хи-квадрат (и использует те же степени свободы). Хотя это не является необходимым для теста Кенкера–Бассета, тест Бреуша–Пагана требует, чтобы квадраты остатков также были разделены на сумму квадратов остатков, деленную на размер выборки. ^[22] Тестирование на групповую гетероскедастичность можно выполнить с помощью теста Голдфельда–Квандта . ^[23]

Из-за стандартного использования стандартных ошибок, соответствующих гетероскедастичности , и проблемы предварительного теста эконометристы в настоящее время редко используют тесты на условную гетероскедастичность. ^[6]

Список тестов

Хотя тесты на гетероскедастичность между группами формально можно рассматривать как частный случай тестирования в рамках регрессионных моделей, некоторые тесты имеют структуры, специфичные для этого случая.

Тесты в регрессии

• Тест Гольдфельда-Квандта
• Тест в парке ^[24]
• Тест Глейзера ^{[25] [26]}
• Тест Харрисона-Маккейба
• Тест Бреуша–Пагана
• Белый тест ^[2]
• Тест Кука-Вайсберга

Тесты для сгруппированных данных

• F-тест равенства дисперсий
• Тест Кохрана C
• тест Хартли
• тест Бартлетта
• тест Левена
• Тест Брауна-Форсайта

Обобщения

Гомоскедастические распределения

Два или более нормальных распределения являются гомоскедастичными и не имеют последовательной корреляции , если они имеют одни и те же диагонали в своей ковариационной матрице, а их недиагональные элементы равны нулю. Гомоскедастичные распределения особенно полезны для получения статистических алгоритмов распознавания образов и машинного обучения . Одним из популярных примеров алгоритма, который предполагает гомоскедастичность, является линейный дискриминантный анализ Фишера . Концепция гомоскедастичности может быть применена к распределениям на сферах. ^[27] ${\displaystyle N(\mu _{1},\Sigma _{1}),N(\mu _{2},\Sigma _{2}),}$ ${\displaystyle \Sigma _{1}{ii}=\Sigma _{2}{jj},\ \forall i=j.}$

Многомерные данные

Изучение хоумскедастичности и гетероскедастичности было обобщено на многомерный случай, который имеет дело с ковариациями векторных наблюдений вместо дисперсии скалярных наблюдений. Одна из версий этого заключается в использовании ковариационных матриц в качестве многомерной меры дисперсии. Несколько авторов рассматривали тесты в этом контексте как для регрессии, так и для ситуаций с группированными данными. ^{[28] [29]} Тест Бартлетта на гетероскедастичность между сгруппированными данными, используемый чаще всего в одномерном случае, также был расширен для многомерного случая, но приемлемое решение существует только для 2 групп. ^[30] Существуют приближения для более чем двух групп, и оба они называются тестом Бокса M.

Смотрите также

• Гетерогенность
• Сферическая ошибка
• Гетероскедастичность-согласованные стандартные ошибки

Ссылки

1. О греческой этимологии термина см. McCulloch, J. Huston (1985). "On Heteros*edasticity". Econometrica . 53 (2): 483. JSTOR  1911250.
2. Уайт, Хэлберт (1980). «Согласованная с гетероскедастичностью ковариационная матрица оценки и прямой тест на гетероскедастичность». Econometrica . 48 (4): 817–838. CiteSeerX 10.1.1.11.7646 . doi :10.2307/1912934. JSTOR  1912934.  
3. Gujarati, DN; Porter, DC (2009). Basic Econometrics (Пятое изд.). Бостон: McGraw-Hill Irwin. стр. 400. ISBN  9780073375779.
4. Голдбергер, Артур С. (1964). Эконометрическая теория . Нью-Йорк: John Wiley & Sons. С. 238–243. ISBN 9780471311010.
5. Джонстон, Дж. (1972). Эконометрические методы . Нью-Йорк: McGraw-Hill. С. 214–221.
6. Angrist, Joshua D.; Pischke, Jörn-Steffen (2009-12-31). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. doi : 10.1515/9781400829828. ISBN 978-1-4008-2982-8.
7. Лонг, Дж. Скотт ; Триведи, Правин К. (1993). «Некоторые тесты спецификации для модели линейной регрессии». В Боллен, Кеннет А.; Лонг, Дж. Скотт (ред.). Тестирование моделей структурных уравнений . Лондон: Sage. стр. 66–110. ISBN 978-0-8039-4506-7.
8. Энгл, Роберт Ф. (июль 1982 г.). «Авторегрессионная условная гетероскедастичность с оценками дисперсии инфляции в Соединенном Королевстве». Econometrica . 50 (4): 987–1007. doi :10.2307/1912773. ISSN  0012-9682. JSTOR  1912773.
9. Питер Кеннеди, Руководство по эконометрике , 5-е издание, стр. 137.
10. Джинадаса, Гамадж; Вираханди, Сэм (1998). "Характеристика размера некоторых тестов в однофакторном дисперсионном анализе". Communications in Statistics - Simulation and Computation . 27 (3): 625. doi :10.1080/03610919808813500.
11. Батке, А. (2004). «Тест ANOVA F все еще может использоваться в некоторых сбалансированных планах с неравными дисперсиями и ненормальными данными». Журнал статистического планирования и вывода . 126 (2): 413–422. doi :10.1016/j.jspi.2003.09.010.
12. Фокс, Дж. (1997). Прикладной регрессионный анализ, линейные модели и связанные с ними методы . Калифорния: Sage Publications. стр. 306.(Цитируется в Gujarati et al. 2009, стр. 400)
13. Мэнкью, НГ (1990). «Краткий курс по макроэкономике». Журнал экономической литературы . 28 (4): 1645–1660 [стр. 1648]. doi : 10.3386/w3256 . JSTOR  2727441.
14. Джайлс, Дэйв (8 мая 2013 г.). «Надежные стандартные ошибки для нелинейных моделей». Econometrics Beat .
15. Gourieroux, C.; Monfort, A.; Trognon, A. (1984). «Псевдомаксимальные методы правдоподобия: теория». Econometrica . 52 (3): 681–700. doi :10.2307/1913471. ISSN  0012-9682.
16. Гинкер, Т.; Либерман, О. (2017). «Устойчивость моделей бинарного выбора к условной гетероскедастичности». Economics Letters . 150 : 130–134. doi :10.1016/j.econlet.2016.11.024.
17. Грин, Уильям Х. (2012). «Оценка и вывод в моделях бинарного выбора». Эконометрический анализ (седьмое изд.). Бостон: Pearson Education. стр. 730–755 [стр. 733]. ISBN 978-0-273-75356-8.
18. Tofallis, C (2008). «Процентная регрессия по методу наименьших квадратов». Журнал современных прикладных статистических методов . 7 : 526–534. doi :10.2139/ssrn.1406472. SSRN  1406472.
19. JNK Rao (март 1973 г.). «Об оценке гетероскедастических дисперсий». Биометрия . 29 (1): 11–24. doi :10.2307/2529672. JSTOR  2529672.
20. Бреуш, ТС; Паган, АР (1979). «Простой тест на гетероскедастичность и случайную дисперсию коэффициентов». Econometrica . 47 (5): 1287–1294. doi :10.2307/1911963. ISSN  0012-9682. JSTOR  1911963.
21. Улла, Мухаммад Имдад (2012-07-26). "Тест Брейша-Пагана на гетероскедастичность". Базовая статистика и анализ данных . Получено 2020-11-28 .
22. Pryce, Gwilym. "Гетероскедастичность: тестирование и исправление в SPSS" (PDF) . стр. 12–18. Архивировано (PDF) из оригинала 2017-03-27 . Получено 26 марта 2017 .
23. Баум, Кристофер Ф. (2006). «Stata Tip 38: Testing for Groupwise Heteroskedasticity». The Stata Journal: Promoting Communications on Statistics and Stata . 6 (4): 590–592. doi : 10.1177/1536867X0600600412 . ISSN  1536-867X. S2CID  117349246.
24. RE Park (1966). «Оценка с гетероскедастическими членами ошибки». Econometrica . 34 (4): 888. doi :10.2307/1910108. JSTOR  1910108.
25. Glejser, H. (1969). «Новый тест на гетероскедастичность». Журнал Американской статистической ассоциации . 64 (325): 316–323. doi :10.1080/01621459.1969.10500976.
26. Мачадо, Хосе А.Ф.; Сильва, JMC Сантос (2000). «Повторный тест Глейзера». Журнал эконометрики . 97 (1): 189–202. дои : 10.1016/S0304-4076(00)00016-6.
27. Хамсичи, Онур К.; Мартинес, Алейкс М. (2007) «Сферически-гомоскедастические распределения: эквивалентность сферических и нормальных распределений в классификации», Журнал исследований машинного обучения , 8, 1583-1623
28. Хольгерссон, ХЕТ; Шукур, Г. (2004). «Тестирование на многомерную гетероскедастичность». Журнал статистических вычислений и моделирования . 74 (12): 879. doi :10.1080/00949650410001646979. hdl : 2077/24416 . S2CID  121576769.
29. Гупта, АК; Тан, Дж. (1984). «Распределение статистики отношения правдоподобия для проверки равенства ковариационных матриц многомерных гауссовых моделей». Biometrika . 71 (3): 555–559. doi :10.1093/biomet/71.3.555. JSTOR  2336564.
30. d'Agostino, RB; Russell, HK (2005). "Многомерный тест Бартлетта". Энциклопедия биостатистики . doi :10.1002/0470011815.b2a13048. ISBN 978-0470849071.

Дальнейшее чтение

Большинство учебников по статистике будут включать по крайней мере некоторые материалы по гомоскедастичности и гетероскедастичности. Вот некоторые примеры:

• Астериу, Димитрос; Холл, Стивен Г. (2011). Прикладная эконометрика (второе изд.). Palgrave MacMillan. стр. 109–147. ISBN 978-0-230-27182-1.
• Дэвидсон, Рассел; Маккиннон, Джеймс Г. (1993). Оценка и вывод в эконометрике. Нью-Йорк: Oxford University Press. С. 547–582. ISBN 978-0-19-506011-9.
• Догерти, Кристофер (2011). Введение в эконометрику. Нью-Йорк: Oxford University Press. С. 280–299. ISBN 978-0-19-956708-9.
• Гуджарати, Дамодар Н.; Портер , Дон К. (2009). Основы эконометрики (Пятое изд.). Нью-Йорк: McGraw-Hill Irwin. С. 365–411. ISBN 978-0-07-337577-9.
• Кмента, Ян (1986). Элементы эконометрики (Второе издание). Нью-Йорк: Macmillan. С. 269–298. ISBN 978-0-02-365070-3.
• Маддала, Г.С .; Лахири, Каджал (2009). Введение в эконометрику (четвертое издание). Нью-Йорк: Wiley. С. 211–238. ISBN 978-0-470-01512-4.

Внешние ссылки

• Лекция по эконометрике (тема: гетероскедастичность) на YouTube от Марка Тома