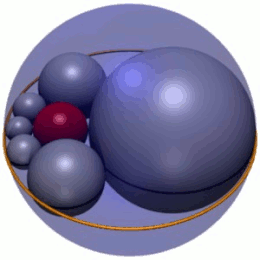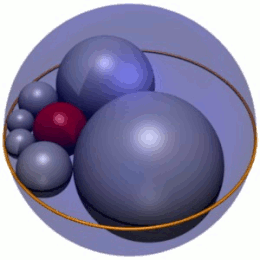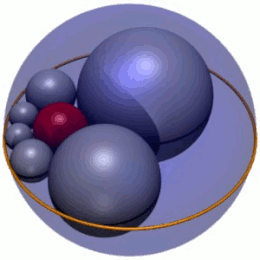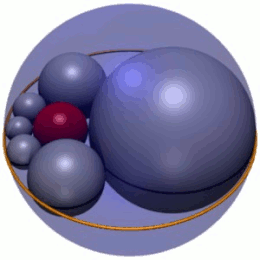
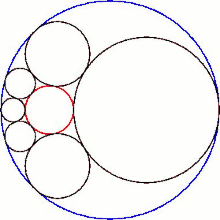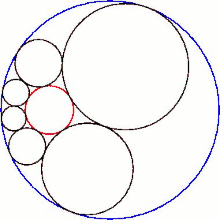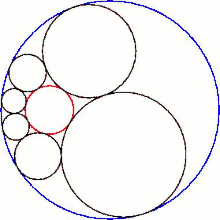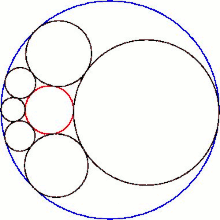
В геометрии гекслет Содди представляет собой цепочку из шести сфер (показанных серым цветом на рисунке 1), каждая из которых касается обеих своих соседей, а также трех взаимно касающихся данных сфер. На рисунке 1 три сферы — это красная внутренняя сфера и две сферы (не показаны) выше и ниже плоскости, на которой лежат центры сфер гекслета. Кроме того, сферы гекслета касаются четвертой сферы (синяя внешняя сфера на рисунке 1), которая не касается трех других.
Согласно теореме, опубликованной Фредериком Содди в 1937 году, [1] всегда можно найти гекслет для любого выбора взаимно касающихся сфер A , B и C. Действительно, существует бесконечное семейство гекслетов, связанных вращением и масштабированием сфер гекслетов (рисунок 1); в этом случае гекслет Содди является сферическим аналогом цепи Штейнера из шести окружностей. [2] В соответствии с цепями Штейнера, центры сфер гекслетов лежат в одной плоскости на эллипсе. Гекслет Содди был также открыт независимо в Японии, как показано на табличках Сангаку 1822 года в префектуре Канагава. [3]
Гекслет Содди представляет собой цепочку из шести сфер, обозначенных S 1 – S 6 , каждая из которых касается трех заданных сфер, A , B и C , которые сами по себе касаются друг друга в трех различных точках. (Для единообразия в статье сферы гекслета всегда будут изображены серым цветом, сферы A и B – зеленым, а сфера C – синим.) Сферы гекслета также касаются четвертой фиксированной сферы D (всегда показанной красным), которая не касается трех других, A , B и C .
Каждая сфера гекслета Содди также касается своих соседей в цепочке; например, сфера S 4 касается S 3 и S 5 . Цепь замкнута, что означает, что каждая сфера в цепочке имеет двух касательных соседей; в частности, начальная и конечная сферы, S 1 и S 6 , касаются друг друга.

Кольцевой гекслет Содди является особым случаем (рисунок 2), в котором три взаимно касающиеся сферы состоят из одной сферы радиуса r (синяя), зажатой между двумя параллельными плоскостями (зеленая), разделенными перпендикулярным расстоянием 2 r . В этом случае гекслет Содди состоит из шести сфер радиуса r , упакованных как шарикоподшипники вокруг центральной сферы и также зажатых. Сферы гекслета также касаются четвертой сферы (красной), которая не касается остальных трех.
Цепочку из шести сфер можно вращать вокруг центральной сферы, не затрагивая их касательных, что показывает, что для этого случая существует бесконечное семейство решений. При вращении сферы гекслета вычерчивают тор ( поверхность в форме бублика); другими словами, тор является оболочкой этого семейства гекслетов.
Общая задача нахождения гекслета для трех данных взаимно касающихся сфер A , B и C может быть сведена к кольцевому случаю с помощью инверсии . Эта геометрическая операция всегда преобразует сферы в сферы или в плоскости, которые можно рассматривать как сферы бесконечного радиуса. Сфера преобразуется в плоскость тогда и только тогда, когда сфера проходит через центр инверсии. Преимущество инверсии в том, что она сохраняет касание; если две сферы были касательными до преобразования, они остаются таковыми и после. Таким образом, если преобразование инверсии выбрано разумно, задачу можно свести к более простому случаю, такому как кольцевой гекслет Содди. Инверсия обратима; повторение инверсии в той же точке возвращает преобразованные объекты к их исходному размеру и положению.
Инверсия в точке касания сфер A и B преобразует их в параллельные плоскости, которые можно обозначить как a и b . Поскольку сфера C касается как A, так и B и не проходит через центр инверсии, C преобразуется в другую сферу c , которая касается обеих плоскостей; следовательно, c зажата между двумя плоскостями a и b . Это кольцевой гекслет Содди (рисунок 2). Шесть сфер s 1 – s 6 могут быть упакованы вокруг c и также зажаты между ограничивающими плоскостями a и b . Повторная инверсия восстанавливает три исходные сферы и преобразует s 1 – s 6 в гекслет для исходной задачи. В общем случае эти гекслеты сфер S 1 – S 6 имеют разные радиусы.
Бесконечное множество гекслетов может быть получено путем вращения шести шаров s 1 – s 6 в их плоскости на произвольный угол перед их повторным инвертированием. Оболочка, полученная в результате таких вращений, представляет собой тор , который окружает сферу c и зажат между двумя плоскостями a и b ; таким образом, тор имеет внутренний радиус r и внешний радиус 3 r . После повторного инвертирования этот тор становится циклидой Дюпена (рисунок 3).

Огибающая гекслетов Содди — это циклида Дюпена , инверсия тора . Таким образом, построение Содди показывает, что циклида Дюпена является огибающей однопараметрического семейства сфер двумя различными способами, и каждая сфера в любом семействе касается двух сфер в том же семействе и трех сфер в другом семействе. [4] Этот результат, вероятно, был известен Шарлю Дюпену , который открыл циклиды, носящие его имя, в своей диссертации 1803 года под руководством Гаспара Монжа . [5]
Пересечение гекслета с плоскостью его сферических центров образует цепочку Штейнера из шести окружностей.
Предполагается, что сферы A и B имеют одинаковый размер.
В любом эллиптическом гекслете, таком как показанный в верхней части статьи, есть две касательные плоскости к гекслету. Для того чтобы существовал эллиптический гекслет, радиус C должен быть меньше одной четверти радиуса A. Если радиус C составляет одну четверть радиуса A , каждая сфера станет плоскостью в пути. Однако инвертированное изображение показывает нормальный эллиптический гекслет, а в параболическом гекслете точка, в которой сфера превращается в плоскость, находится именно тогда, когда ее инвертированное изображение проходит через центр инверсии. В таком гекслете есть только одна касательная плоскость к гекслету. Линия центров параболического гекслета является параболой.
Если C еще больше, то образуется гиперболический гекслет, и теперь касательных плоскостей нет вообще. Обозначим сферы как S 1 - S 6 . Таким образом, S 1 не может уйти слишком далеко, пока не станет плоскостью (где ее перевернутое изображение проходит через центр инверсии), а затем не изменит свою вогнутость (где ее перевернутое изображение окружает центр инверсии). Теперь линия центров является гиперболой.
Предельный случай — когда A , B и C имеют одинаковый размер. Теперь гекслет становится прямым. S 1 становится маленьким, поскольку он проходит через отверстие между A , B и C , и растет, пока не станет плоскостью, касательной к ним. Центр инверсии теперь также имеет точку касания с образом S 6 , поэтому он также является плоскостью, касательной к A , B и C . По мере продвижения S 1 его вогнутость меняется на противоположную, и теперь он окружает все остальные сферы, касательные к A , B , C , S 2 и S 6 . S 2 выталкивается вверх и растет, чтобы стать касательной плоскостью, а S 6 сжимается. Затем S 1 получает прежнее положение S 6 как касательной плоскости. Затем он снова меняет вогнутость и снова проходит через отверстие, начиная еще один круговой путь. Теперь линия центров представляет собой вырожденную гиперболу, где она схлопнулась в две прямые линии. [2]


Японские математики открыли тот же гекслет более чем за сто лет до Содди. Они анализировали проблемы упаковки, в которых соприкасаются круги и многоугольники, шары и многогранники, и часто находили соответствующие теоремы независимо до их открытия западными математиками. Они часто публиковали их как сангаку . Сангаку о гекслете была сделана Ирисавой Синтаро Хироацу в школе Учида Ицуми и посвящена святилищу Самукава в мае 1822 года. Оригинал сангаку был утерян, но был записан в книге Учида Коконсанкан в 1832 году. Копия сангаку была сделана по записи и посвящена музею Хотоку в святилище Самукава в августе 2009 года. [6]
Сангаку Ирисавы состоит из трех задач. Третья задача относится к гекслету Содди: «диаметр внешней описывающей сферы составляет 30 солнц . Диаметры ядерных шаров составляют 10 солнц и 6 солнц каждый. Диаметр одного из шаров в цепочке шаров составляет 5 солнц. Затем я спросил о диаметрах оставшихся шаров. Ответ: 15 солнц, 10 солнц, 3,75 солнц, 2,5 солнц и 2 + 8/11 солнц». [7]
В его ответе метод вычисления диаметров шаров записан и, будучи преобразован в математическую нотацию , дает следующее решение. Если отношения диаметра внешнего шара к каждому из шаров ядра равны a 1 , a 2 , и если отношения диаметра к цепным шарам равны c 1 , ..., c 6 , мы хотим представить c 2 , ..., c 6 через a 1 , a 2 и c 1 . Если
затем,
Тогда с1 + с4 = с2 + с5 = с3 + с6 .
Если r 1 , ..., r 6 — диаметры шести шаров, то получаем формулу: