Гемодинамика

Динамика кровотока

Гемодинамика или гемодинамика — это динамика кровотока . Система кровообращения контролируется гомеостатическими механизмами саморегуляции , так же как гидравлические контуры контролируются системами управления . Гемодинамический ответ непрерывно отслеживает и подстраивается под условия в организме и его окружающей среде. Гемодинамика объясняет физические законы , которые управляют потоком крови в кровеносных сосудах .

Кровоток обеспечивает транспортировку питательных веществ , гормонов , продуктов метаболизма, кислорода и углекислого газа по всему телу для поддержания метаболизма на уровне клеток , регуляции pH , осмотического давления и температуры всего тела, а также защиты от микробного и механического повреждения. ^[1]

Кровь — неньютоновская жидкость , и ее изучение наиболее эффективно с помощью реологии, а не гидродинамики. Поскольку кровеносные сосуды не являются жесткими трубками, классическая гидродинамика и механика жидкостей, основанная на использовании классических вискозиметров, не способны объяснить гемодинамику. ^[2]

Изучение кровотока называется гемодинамикой, а изучение свойств кровотока — гемореологией .

Кровь

Кровь — сложная жидкость. Кровь состоит из плазмы и форменных элементов . Плазма содержит 91,5% воды, 7% белков и 1,5% других растворенных веществ. Форменными элементами являются тромбоциты , лейкоциты и эритроциты . Наличие этих форменных элементов и их взаимодействие с молекулами плазмы являются основными причинами, по которым кровь так сильно отличается от идеальных ньютоновских жидкостей. ^[1]

Вязкость плазмы

Нормальная плазма крови ведет себя как ньютоновская жидкость при физиологических скоростях сдвига. Типичные значения вязкости нормальной человеческой плазмы при 37 °C составляют 1,4 мН·с/м ² . ^[3] Вязкость нормальной плазмы изменяется в зависимости от температуры таким же образом, как и вязкость ее растворяющей воды ^[4] ; изменение температуры на 3 °C в физиологическом диапазоне (от 36,5 °C до 39,5 °C) снижает вязкость плазмы примерно на 10%. ^[5]

Осмотическое давление плазмы

Осмотическое давление раствора определяется числом присутствующих частиц и температурой . Например, 1 молярный раствор вещества содержит6,022 × 1023 ^{молекул} на литр этого вещества и при 0 °C оно имеет осмотическое давление 2,27 МПа (22,4 атм). Осмотическое давление плазмы влияет на механику кровообращения несколькими способами. Изменение разницы осмотического давления на мембране клетки крови вызывает сдвиг воды и изменение объема клетки. Изменения формы и гибкости влияют на механические свойства цельной крови. Изменение осмотического давления плазмы изменяет гематокрит, то есть объемную концентрацию эритроцитов в цельной крови за счет перераспределения воды между внутрисосудистым и внесосудистым пространствами. Это, в свою очередь, влияет на механику цельной крови. ^[6]

Красные кровяные клетки

Эритроцит очень гибок и имеет двояковогнутую форму. Его мембрана имеет модуль Юнга в районе 106  Па . Деформация в эритроцитах вызывается сдвиговым напряжением. Когда суспензия сдвигается, эритроциты деформируются и вращаются из-за градиента скорости, причем скорость деформации и вращения зависит от скорости сдвига и концентрации. Это может повлиять на механику циркуляции и может усложнить измерение вязкости крови . Верно , что в стационарном потоке вязкой жидкости через твердое сферическое тело, погруженное в жидкость, где мы предполагаем, что инерция в таком потоке пренебрежимо мала, считается, что направленная вниз сила гравитации частицы уравновешивается силой вязкого сопротивления. Из этого баланса сил можно показать, что скорость падения определяется законом Стокса ^{[ требуется ссылка ]}

${\displaystyle U_{s}={\frac {2}{9}}{\frac {\left(\rho _{p}-\rho _{f}\right)}{\mu }}g\,a^{2}}$^[6]

Где a — радиус частицы, ρ _p , ρ _f — соответственно плотность частицы и жидкости, μ — вязкость жидкости, g — ускорение свободного падения. Из приведенного выше уравнения видно, что скорость седиментации частицы зависит от квадрата радиуса. Если частица освобождается из состояния покоя в жидкости , ее скорость седиментации U _s увеличивается до тех пор, пока не достигнет устойчивого значения, называемого конечной скоростью (U), как показано выше. ^{[ необходима цитата ]}

Гемодилюция

Гемодилюция — это разбавление концентрации эритроцитов и компонентов плазмы путем частичной замены крови коллоидами или кристаллоидами . Это стратегия, позволяющая избежать воздействия на пациентов потенциальных опасностей переливания гомологичной крови. ^{[7] [8]}

Гемодилюция может быть нормоволемической, что подразумевает разбавление нормальных компонентов крови с помощью расширителей. Во время острой нормоволемической гемодилюции (ANH) кровь, впоследствии потерянная во время операции, содержит пропорционально меньше эритроцитов на миллилитр, что сводит к минимуму интраоперационную потерю цельной крови. Таким образом, кровь, потерянная пациентом во время операции, на самом деле не теряется пациентом, поскольку этот объем очищается и перенаправляется в пациента. ^{[ необходима цитата ]}

С другой стороны, гиперволемическая гемодилюция (ГВГ) использует острое предоперационное расширение объема без удаления крови. Однако при выборе жидкости необходимо убедиться, что при смешивании оставшаяся кровь ведет себя в микроциркуляции так же, как и исходная кровяная жидкость, сохраняя все свои свойства вязкости . [ ^9]

В одном исследовании, показывающем, какой объем ANH следует применять, предлагается математическая модель ANH, которая вычисляет максимально возможную экономию ОКМ с использованием ANH, учитывая вес пациентов H _i и H _m . ^{[ необходима цитата ]}

Для поддержания нормоволемии изъятие аутологичной крови должно быть одновременно замещено подходящим гемодилютом. В идеале это достигается путем изоволемического обменного переливания плазмозаменителя с коллоидно- осмотическим давлением (OP). Коллоид — это жидкость, содержащая частицы, которые достаточно велики, чтобы оказывать онкотическое давление на микрососудистую мембрану. При обсуждении использования коллоида или кристаллоида необходимо учитывать все компоненты уравнения Старлинга:

${\displaystyle \ Q=K([P_{c}-P_{i}]S-[P_{c}-P_{i}])}$

Для определения минимального безопасного гематокрита, желательного для данного пациента, полезно следующее уравнение: ^{[ необходима ссылка ]}

${\displaystyle \ BL_{s}=EBV\ln {\frac {H_{i}}{H_{m}}}}$

где EBV — предполагаемый объем крови ; в этой модели использовалось 70 мл/кг, а H _i (начальный гематокрит) — начальный гематокрит пациента. Из приведенного выше уравнения ясно, что объем крови, удаленной во время ANH до H _m, такой же, как BL _s . Количество крови, которое необходимо удалить, обычно зависит от веса, а не от объема. Количество единиц, которое необходимо удалить для гемодилюции до максимально безопасного гематокрита (ANH), можно найти по формуле

${\displaystyle ANH={\frac {BL_{s}}{450}}}$

Это основано на предположении, что каждая единица, удаленная путем гемодилюции, имеет объем 450 мл (фактический объем единицы будет несколько отличаться, поскольку завершение сбора зависит от веса, а не от объема). Модель предполагает, что значение гемодилюции равно H m _до операции, поэтому повторное переливание крови, полученной путем гемодилюции, должно начинаться, когда начинается SBL. RCM, доступный для повторного переливания после ANH (RCMm), можно рассчитать из H _i пациента и конечного гематокрита после гемодилюции ( H _m ).

${\displaystyle RCM=EVB\times (H_{i}-H_{m})}$

Максимальный возможный уровень SBL при использовании ANH без падения ниже Hm(BLH) определяется путем предположения, что вся кровь, удаленная во время ANH, возвращается пациенту со скоростью, достаточной для поддержания гематокрита на минимально безопасном уровне.

${\displaystyle BL_{H}={\frac {RCM_{H}}{H_{m}}}}$

Если ANH используется до тех пор, пока SBL не превышает BL _H, то не будет необходимости в переливании крови. Из вышесказанного можно сделать вывод, что H не должен превышать s . Таким образом, разница между BL _H и BL _s представляет собой дополнительную хирургическую кровопотерю ( BL _i ), возможную при использовании ANH.

${\displaystyle \ {BL_{i}}={BL_{H}}-{BL_{s}}}$

Если выразить это в терминах RCM

${\displaystyle {RCM_{i}}={BL_{i}}\times {H_{m}}}$

Где RCM _i — это масса эритроцитов, которую необходимо ввести с использованием гомологичной крови для поддержания H _m, если ANH не используется, а кровопотеря равна BLH. ^{[ необходима ссылка ]}

Используемая модель предполагает, что ANH используется для пациента весом 70 кг с предполагаемым объемом крови 70 мл/кг (4900 мл). Диапазон H _i и H _m был оценен для понимания условий, при которых гемодилюция необходима для пользы пациента. ^{[10] [11]}

Результат

Результаты расчетов модели представлены в таблице, приведенной в приложении, для диапазона H _i от 0,30 до 0,50 с ANH, выполненным до минимального гематокрита от 0,30 до 0,15. При H _i 0,40, если H _m предполагается равным 0,25, то из уравнения выше количество RCM все еще высокое и ANH не требуется, если BL _s не превышает 2303 мл, поскольку гемотокрит не упадет ниже H _m , хотя пять единиц крови должны быть удалены во время гемодилюции. При этих условиях для достижения максимальной выгоды от метода, если используется ANH, не потребуется гомологичная кровь для поддержания H _{m ,} если кровопотеря не превышает 2940 мл. В таком случае ANH может сэкономить максимум 1,1 эквивалента единиц эритроцитарной массы, и переливание гомологичной крови необходимо для поддержания H _m , даже если используется ANH. ^{[ необходима цитата ]} Эту модель можно использовать для определения того, когда ANH может быть использован для данного пациента, а также степени ANH, необходимой для максимизации этой пользы. ^{[ необходима цитата ]}

Например, если H _i составляет 0,30 или меньше, то невозможно сохранить массу эритроцитов, эквивалентную двум единицам гомологичных PRBC, даже если пациент гемодилюирован до H _m 0,15. Это происходит потому, что из уравнения RCM RCM пациента не соответствует уравнению, приведенному выше. Если H _i составляет 0,40, необходимо удалить не менее 7,5 единиц крови во время ANH, что дает H _m 0,20, чтобы сохранить эквивалентность двух единиц. Очевидно, что чем больше H _i и большее количество единиц удаляется во время гемодилюции, тем эффективнее ANH для предотвращения переливания гомологичной крови. Модель здесь разработана для того, чтобы позволить врачам определить, где ANH может быть полезен для пациента, на основе их знаний о H _i , потенциале для SBL и оценке H _m . Хотя в модели использовался пациент весом 70 кг, результат можно применить к любому пациенту. Чтобы применить эти результаты к любой массе тела, любое из значений BLs, BLH и ANHH или PRBC, приведенных в таблице, необходимо умножить на коэффициент, который мы будем называть T.

${\displaystyle T={\frac {\text{patient's weight in kg}}{70}}}$

По сути, рассмотренная выше модель предназначена для прогнозирования максимального RCM, который может спасти ANH. ^{[ необходима цитата ]}

Подводя итог, можно сказать, что эффективность ANH была описана математически с помощью измерений хирургической кровопотери и измерения объема потока крови. Эта форма анализа позволяет точно оценить потенциальную эффективность методов и показывает применение измерений в медицинской сфере. ^[10]

Кровоток

Сердечный выброс

Схема кровеносной системы. SVC/IVC - верхняя / нижняя полая вена,

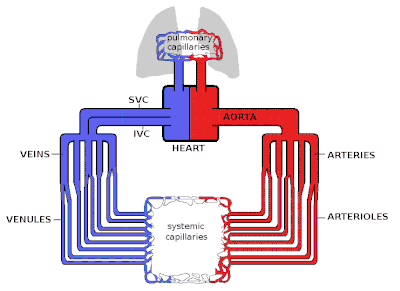
Сердце является двигателем кровеносной системы, качая кровь посредством ритмического сокращения и расслабления. Скорость потока крови из сердца (часто выражаемая в л/мин) известна как сердечный выброс (СВ).

Кровь, выкачиваемая из сердца, сначала попадает в аорту , самую большую артерию тела. Затем она делится на все более мелкие артерии, затем на артериолы и, в конечном итоге, на капилляры , где происходит перенос кислорода. Капилляры соединяются с венулами , и затем кровь возвращается через сеть вен в полые вены в правое сердце . Микроциркуляция — артериолы, капилляры и венулы — составляет большую часть площади сосудистой системы и является местом переноса O ₂ , глюкозы и субстратов ферментов в клетки. Венозная система возвращает дезоксигенированную кровь в правое сердце, где она перекачивается в легкие, чтобы насытиться кислородом, а CO ₂ и другие газообразные отходы обмениваются и выбрасываются во время дыхания. Затем кровь возвращается в левую сторону сердца, где она снова начинает процесс.

В нормальной кровеносной системе объем крови, возвращающийся к сердцу каждую минуту, приблизительно равен объему, который выкачивается каждую минуту (сердечный выброс). ^[12] По этой причине скорость кровотока на каждом уровне кровеносной системы в первую очередь определяется общей площадью поперечного сечения этого уровня.

Сердечный выброс определяется двумя методами. Один из них — с помощью уравнения Фика:

${\displaystyle CO=VO2/C_{a}O_{2}-C_{v}O_{2}}$

Другой метод термодилюции заключается в определении изменения температуры жидкости, введенной в проксимальный порт катетера Свана-Ганца, по сравнению с дистальным портом.

Математически сердечный выброс выражается следующим уравнением:

${\displaystyle CO=SV\times HR}$

где

• СВ = сердечный выброс (л/сек)
• SV = ударный объем (мл)
• ЧСС = частота сердечных сокращений (уд/мин)

Нормальный сердечный выброс человека составляет 5-6 л/мин в состоянии покоя. Не вся кровь, которая попадает в левый желудочек, покидает сердце. То, что остается в конце диастолы (EDV) за вычетом ударного объема, составляет конечный систолический объем (ESV). ^[13]

Анатомические особенности

Кровеносная система видов, подверженных ортостатическому кровяному давлению (например, древесные змеи), развилась с физиологическими и морфологическими особенностями для преодоления нарушения кровообращения. Например, у древесных змей сердце расположено ближе к голове, по сравнению с водными змеями. Это облегчает приток крови к мозгу. ^{[14] [15]}

Турбулентность

На кровоток также влияет гладкость сосудов, что приводит либо к турбулентному (хаотическому), либо к ламинарному (плавному) течению. Плавность снижается из-за накопления жировых отложений на стенках артерий.

Число Рейнольдса (обозначается NR или Re) — это соотношение, которое помогает определить поведение жидкости в трубке, в данном случае крови в сосуде.

Уравнение для этой безразмерной связи записывается как: ^[16]

${\displaystyle NR={\frac {\rho vL}{\mu }}}$

• ρ : плотность крови
• v : средняя скорость крови
• L : характерный размер сосуда, в данном случае диаметр
• μ : вязкость крови

Число Рейнольдса прямо пропорционально скорости и диаметру трубки. Обратите внимание, что NR прямо пропорционально средней скорости, а также диаметру. Число Рейнольдса менее 2300 соответствует ламинарному течению жидкости, которое характеризуется постоянным движением потока, тогда как значение более 4000 соответствует турбулентному течению. ^[16] Из-за меньшего радиуса и самой низкой скорости по сравнению с другими сосудами число Рейнольдса в капиллярах очень низкое, что приводит к ламинарному, а не турбулентному течению. ^[17]

Скорость

Часто выражается в см/с. Это значение обратно пропорционально общей площади поперечного сечения кровеносного сосуда и также отличается для каждого поперечного сечения, поскольку в нормальных условиях кровоток имеет ламинарные характеристики . По этой причине скорость кровотока самая высокая в середине сосуда и самая низкая у стенки сосуда. В большинстве случаев используется средняя скорость. ^[18] Существует много способов измерения скорости кровотока, например, видеокапиллярная микроскопия с покадровым анализом или лазерная допплеровская анемометрия . ^[19] Скорости крови в артериях выше во время систолы , чем во время диастолы . Одним из параметров для количественной оценки этой разницы является индекс пульсативности ( PI ), который равен разнице между пиковой систолической скоростью и минимальной диастолической скоростью, деленной на среднюю скорость во время сердечного цикла . Это значение уменьшается с расстоянием от сердца. ^[20]

${\displaystyle PI={\frac {v_{systole}-v_{diastole}}{v_{mean}}}}$

Кровеносные сосуды

Сосудистое сопротивление

Сопротивление также связано с радиусом сосуда, длиной сосуда и вязкостью крови.

В первом подходе, основанном на жидкостях, как указано в уравнении Хагена-Пуазейля . ^[16] Уравнение выглядит следующим образом:

${\displaystyle \Delta P={\frac {8\mu lQ}{\pi r^{4}}}}$

• ∆ P : падение/градиент давления
• μ : вязкость
• l : длина трубки. В случае сосудов с бесконечно большой длиной l заменяется на диаметр сосуда.
• Q : скорость потока крови в сосуде
• r : радиус судна

Во втором подходе, более реалистичном для сосудистого сопротивления и исходящем из экспериментальных наблюдений за потоками крови, согласно Терстону ^[22], существует наслоение плазмы-клеток на стенках, окружающих закупоренный поток. Это слой жидкости, в котором на расстоянии δ вязкость η является функцией δ, записанной как η(δ), и эти окружающие слои не встречаются в центре сосуда в реальном потоке крови. Вместо этого существует закупоренный поток, который является гипервязким, поскольку содержит высокую концентрацию эритроцитов. Терстон собрал этот слой с сопротивлением потоку, чтобы описать поток крови с помощью вязкости η(δ) и толщины δ от слоя стенки.

Закон сопротивления крови выглядит как R, адаптированный к профилю кровотока:

${\displaystyle R={\frac {cL\eta (\delta )}{(\pi \delta r^{3})}}}$^[22]

где

• R = сопротивление току крови
• c = постоянный коэффициент расхода
• L = длина судна
• η(δ) = вязкость крови в плазматической стенке, высвобождение плазмы - наслаивание клеток
• r = радиус кровеносного сосуда
• δ = расстояние в слое клеток, выделяющих плазму

Сопротивление крови меняется в зависимости от вязкости крови и ее закупоренного потока (или потока оболочки, поскольку они являются дополнительными по сечению сосуда), а также от размера сосудов. Предполагая устойчивый, ламинарный поток в сосуде, поведение кровеносных сосудов похоже на поведение трубы. Например, если p1 и p2 являются давлениями на концах трубки, падение/градиент давления составляет: ^[23]

${\displaystyle {\frac {p_{1}-p_{2}}{l}}=\Delta P}$

Более крупные артерии, включая все достаточно большие, чтобы увидеть их без увеличения, являются проводниками с низким сосудистым сопротивлением (при условии отсутствия прогрессирующих атеросклеротических изменений) с высокой скоростью потока, которая создает лишь небольшие перепады давления. Более мелкие артерии и артериолы имеют более высокое сопротивление и передают основное падение давления крови через крупные артерии капиллярам в кровеносной системе.

Иллюстрация, демонстрирующая, как сужение сосудов (вазоконстрикция) повышает артериальное давление.

В артериолах давление крови ниже, чем в крупных артериях. Это происходит из-за бифуркаций, которые вызывают падение давления. Чем больше бифуркаций, тем выше общая площадь поперечного сечения, поэтому давление на поверхности падает. Вот почему ^{[ необходима цитата ]} артериолы имеют самый высокий перепад давления. Перепад давления артериол является произведением скорости потока и сопротивления: ∆P=Q x сопротивление. Высокое сопротивление, наблюдаемое в артериолах, которое в значительной степени влияет на ∆ P, является результатом меньшего радиуса около 30 мкм. ^[24] Чем меньше радиус трубки, тем больше сопротивление потоку жидкости.

Сразу за артериолами располагаются капилляры. Следуя логике, наблюдаемой в артериолах, мы ожидаем, что давление крови в капиллярах будет ниже по сравнению с артериолами. Поскольку давление является функцией силы на единицу площади ( P  =  F / A ), чем больше площадь поверхности, тем меньше давление, когда на нее действует внешняя сила. Хотя радиусы капилляров очень малы, сеть капилляров имеет самую большую площадь поверхности в сосудистой сети. Известно, что они имеют самую большую площадь поверхности (485 мм^2) в сосудистой сети человека. Чем больше общая площадь поперечного сечения, тем ниже средняя скорость, а также давление. ^[25]

Вещества, называемые вазоконстрикторами, могут уменьшать размер кровеносных сосудов, тем самым повышая артериальное давление. Вазодилататоры (например, нитроглицерин ) увеличивают размер кровеносных сосудов, тем самым снижая артериальное давление.

Если вязкость крови увеличивается (становится гуще), результатом становится повышение артериального давления. Определенные медицинские состояния могут изменить вязкость крови. Например, анемия (низкая концентрация эритроцитов ) снижает вязкость, тогда как повышенная концентрация эритроцитов увеличивает вязкость. Считалось, что аспирин и родственные ему « разжижающие кровь » препараты снижают вязкость крови, но вместо этого исследования показали, что они действуют, уменьшая тенденцию крови к свертыванию. ^[26]

Для определения системного сосудистого сопротивления (ССС) используется формула расчета общего сопротивления.

${\displaystyle R=(\Delta pressure)/flow.}$

Для SVR это означает:

${\displaystyle SVR=(MAP-CVP)/CO}$

Где

• SVR = системное сосудистое сопротивление (мм рт.ст./л/мин)
• САД = среднее артериальное давление (мм рт. ст.)
• ЦВД = центральное венозное давление (мм рт. ст.)
• СВ = сердечный выброс (л/мин) ^[27]

Чтобы получить этот результат в единицах Вуда, ответ умножается на 80.

Нормальное системное сосудистое сопротивление составляет от 900 до 1440 дин/сек/см−5. ^[28]

Натяжение стен

Составляющие напряжения цилиндра .

Независимо от места, артериальное давление связано с натяжением стенки сосуда в соответствии с уравнением Юнга-Лапласа (предполагается, что толщина стенки сосуда очень мала по сравнению с диаметром просвета ) :

${\displaystyle \sigma _{\theta }={\dfrac {Pr}{t}}\ }$

где

• P — артериальное давление
• t — толщина стенки
• r — внутренний радиус цилиндра.
• ${\displaystyle \sigma _{\theta }\!}$напряжение цилиндра или «кольцевое напряжение».

Чтобы предположение о тонкостенности было верным, толщина стенки сосуда должна составлять не более одной десятой (часто упоминается как одна двадцатая) его радиуса.

Напряжение цилиндра , в свою очередь, представляет собой среднюю силу, действующую по окружности (перпендикулярно как оси, так и радиусу объекта) на стенку цилиндра, и может быть описано как:

${\displaystyle \sigma _{\theta }={\dfrac {F}{tl}}\ }$

где:

• F — сила , действующая по окружности на область стенки цилиндра, имеющую следующие две длины сторон:
• t — радиальная толщина цилиндра
• l — осевая длина цилиндра

Стресс

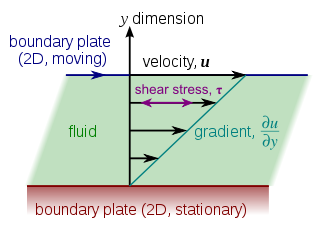
Когда к материалу прикладывается сила, он начинает деформироваться или двигаться. Поскольку сила, необходимая для деформации материала (например, для создания потока жидкости), увеличивается с размером поверхности материала A. ^[6] , величина этой силы F пропорциональна площади A части поверхности. Поэтому величина (F/A), которая является силой на единицу площади, называется напряжением. Касательное напряжение на стенке, которое связано с потоком крови через артерию, зависит от размера артерии и ее геометрии и может находиться в диапазоне от 0,5 до 4 Па . ^[29]

${\displaystyle \sigma ={\frac {F}{A}}}$.

В нормальных условиях, чтобы избежать атерогенеза, тромбоза, пролиферации гладких мышц и апоптоза эндотелия, напряжение сдвига сохраняет свою величину и направление в приемлемом диапазоне. В некоторых случаях, возникающих из-за кровяного молота, напряжение сдвига достигает больших значений. При этом направление напряжения может также изменяться обратным потоком в зависимости от гемодинамических условий. Следовательно, эта ситуация может привести к заболеванию атеросклерозом. ^[30]

Ламинарный сдвиг жидкости между двумя пластинами. Трение между жидкостью и движущимися границами заставляет жидкость сдвигаться (течь). Сила, необходимая для этого действия на единицу площади, называется напряжением. Соотношение между напряжением (силой) и скоростью сдвига (скоростью потока) определяет вязкость. ${\displaystyle v=u,\tau =\sigma }$

Емкость

Вены описываются как «емкостные сосуды» тела, поскольку более 70% объема крови находится в венозной системе. Вены более податливы, чем артерии, и расширяются, чтобы приспособиться к изменяющемуся объему. ^[31]

Артериальное давление

Давление крови в системе кровообращения в основном обусловлено насосным действием сердца. ^[32] Насосное действие сердца создает пульсирующий поток крови, который проводится в артерии, через микроциркуляцию и в конечном итоге обратно через венозную систему к сердцу. Во время каждого сердечного сокращения системное артериальное давление крови изменяется между максимальным ( систолическим ) и минимальным ( диастолическим ) давлением. ^[33] В физиологии они часто упрощаются до одного значения, среднего артериального давления (САД) , которое рассчитывается следующим образом:

${\displaystyle MAP=DP+1/3(PP)}$

где:

• САД = среднее артериальное давление
• DP = диастолическое артериальное давление
• PP = Пульсовое давление, которое равно систолическому давлению минус диастолическое давление. ^[34]

Различия в среднем кровяном давлении отвечают за поток крови из одного места в другое в системе кровообращения. Скорость среднего кровотока зависит как от кровяного давления, так и от сопротивления потоку, оказываемого кровеносными сосудами. Среднее кровяное давление уменьшается по мере того, как циркулирующая кровь движется от сердца через артерии и капилляры из-за вязких потерь энергии. Среднее кровяное давление падает по всему кругу кровообращения, хотя большая часть падения происходит вдоль мелких артерий и артериол . ^[35] Гравитация влияет на кровяное давление через гидростатические силы (например, во время стояния), а клапаны в венах, дыхание и перекачивание крови за счет сокращения скелетных мышц также влияют на кровяное давление в венах. ^[32]

Связь между давлением, расходом и сопротивлением выражается следующим уравнением: ^[12]

${\displaystyle Flow=Pressure/Resistance}$

Применительно к кровеносной системе мы получаем:

${\displaystyle CO=(MAP-RAP)/SVR}$

где

• СВ = сердечный выброс (в л/мин)
• САД = среднее артериальное давление (в мм рт. ст.), среднее давление крови, покидающей сердце
• ДПП = давление в правом предсердии (в мм рт. ст.), среднее давление крови при ее возвращении в сердце
• SVR = системное сосудистое сопротивление (в мм рт. ст. * мин/л)

Упрощенная форма этого уравнения предполагает, что давление в правом предсердии приблизительно равно 0:

${\displaystyle CO\approx MAP/SVR}$

Идеальное кровяное давление в плечевой артерии , где стандартные манжеты для измерения кровяного давления измеряют давление, составляет <120/80 мм рт. ст. Другие крупные артерии имеют схожие уровни регистрации кровяного давления, что указывает на очень низкие различия между крупными артериями. В безымянной артерии среднее показание составляет 110/70 мм рт. ст., в правой подключичной артерии в среднем 120/80, а в брюшной аорте — 110/70 мм рт. ст. ^[25] Относительно равномерное давление в артериях указывает на то, что эти кровеносные сосуды действуют как резервуар давления для жидкостей, которые транспортируются внутри них.

Давление постепенно падает по мере того, как кровь течет из крупных артерий через артериолы, капилляры, пока кровь не будет вытолкнута обратно в сердце через венулы, вены через полую вену с помощью мышц. При любом данном падении давления скорость потока определяется сопротивлением кровотоку. В артериях, при отсутствии заболеваний, сопротивление крови очень мало или отсутствует. Диаметр сосуда является наиболее важным фактором для контроля сопротивления. По сравнению с другими более мелкими сосудами в организме, артерия имеет гораздо больший диаметр (4 мм), поэтому сопротивление низкое. ^[25]

Градиент рука -нога (артериальное давление) — это разница между артериальным давлением, измеренным на руках, и артериальным давлением, измеренным на ногах. Обычно он меньше 10 мм рт. ст., ^[36] но может быть увеличен, например, при коарктации аорты . ^[36]

Клиническое значение

Мониторинг давления

Наркозный аппарат с интегрированными системами мониторинга нескольких гемодинамических параметров, включая артериальное давление и частоту сердечных сокращений.

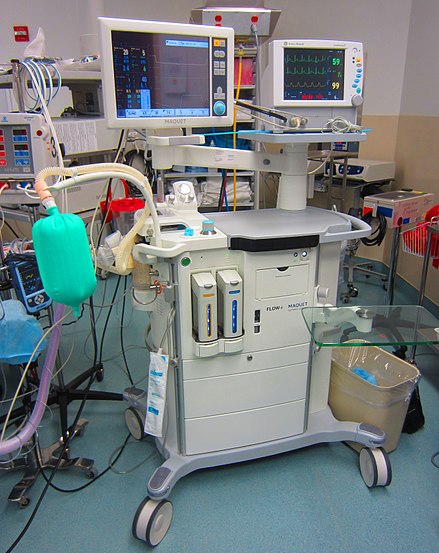
Гемодинамический мониторинг — это наблюдение за гемодинамическими параметрами с течением времени, такими как артериальное давление и частота сердечных сокращений . Артериальное давление можно контролировать либо инвазивно с помощью вставленного датчика артериального давления (обеспечивающего непрерывный мониторинг), либо неинвазивно, многократно измеряя артериальное давление с помощью надувной манжеты для измерения артериального давления .

Гипертония диагностируется при наличии артериального давления 140/90 или выше в течение двух клинических визитов. ^[27]

Давление заклинивания легочной артерии может показать наличие застойной сердечной недостаточности, нарушений митрального и аортального клапанов, гиперволемии , шунтов или тампонады сердца. ^[37]

Дистанционный, косвенный мониторинг кровотока с помощью лазерной допплерографии

Лазерная допплерография выявляет кровоток в сетчатке

Неинвазивный гемодинамический мониторинг сосудов глазного дна может быть выполнен с помощью лазерной допплеровской голографии с ближним инфракрасным светом. Глаз предлагает уникальную возможность для неинвазивного исследования сердечно-сосудистых заболеваний . Лазерная допплеровская визуализация с помощью цифровой голографии может измерять кровоток в сетчатке и сосудистой оболочке , чьи допплеровские ответы демонстрируют импульсный профиль со временем ^{[38] [39]} Эта техника позволяет проводить неинвазивную функциональную микроангиографию путем высококонтрастного измерения допплеровских ответов из эндолюминальных профилей кровотока в сосудах заднего сегмента глаза. Различия в артериальном давлении управляют потоком крови по всему кругу кровообращения. Скорость среднего кровотока зависит как от артериального давления, так и от гемодинамического сопротивления потоку, представляемого кровеносными сосудами.

Глоссарий

АНХ

Острая нормоволемическая гемодилюция

АНХ _у

Количество единиц в течение ANH

БЛ _Х

Максимально возможная кровопотеря при использовании АНГ до того, как потребуется переливание гомологичной крови

БЛ _I

Возможна дополнительная кровопотеря при АНГ. (BL _H – BL _s )

БЛ _с

Максимальная кровопотеря без АНГ перед необходимостью переливания гомологичной крови

ВЭБ

Расчетный объем крови (70 мл/кг)

Hct

Гематокрит здесь всегда выражается в виде дроби

Привет_​

Начальный гематокрит

Н _м

Минимальный безопасный гематокрит

ПРБК

Эквивалент упакованных эритроцитов, сохраненный ANH

РКМ

Эритроцитная масса.

РКМ _Н

Клеточная масса, доступная для переливания после АНГ

РКМ _I

Масса эритроцитов, сохраненная ANH

СБЛ

Хирургическая кровопотеря

Этимология и произношение

Слово гемодинамика ( / ˌ h iː m ə d aɪ ˈ n æ m ɪ k s , - m oʊ -/ ^[40] ) использует сочетающиеся формы hemo- ( которое происходит от древнегреческого haima , что означает кровь) и dynamics , таким образом , « динамика крови ». Гласная слога hemo- пишется по-разному в соответствии с вариацией ae/e .

• Кровавый молот
• Артериальное давление
• Сердечный выброс
• Общество динамики сердечно-сосудистой системы
• Электрокардиометрия
• Эзофагеальная допплерография
• Гемодинамика аорты
• Импедансная кардиография
• Фотоплетизмограмма
• Лазерная допплерография
• эффект Виндкесселя
• Функциональная ближняя инфракрасная спектроскопия

Примечания и ссылки

1. Tortora, Gerard J.; Derrickson, Bryan (2012). «Сердечно-сосудистая система: Кровь». Principles of Anatomy & Physiology (13-е изд.). John Wiley & Sons. стр. 729–732. ISBN 978-0-470-56510-0.
2. Fieldman, Joel S.; Phong, Duong H.; Saint-Aubin, Yvan; Vinet, Luc (2007). «Реология». Биология и механика кровотока, часть II: Механика и медицинские аспекты . Springer. стр. 119–123. ISBN 978-0-387-74848-1.
3. Рэнд, Питер (31 мая 1963 г.). «Кровь человека при нормотермических и гипотермических условиях» (PDF) . Журнал прикладной физиологии . 19 : 117–122. doi :10.1152/jappl.1964.19.1.117. PMID  14104265 . Получено 16 сентября 2014 г. .^{[ постоянная мертвая ссылка ‍ ]}
4. Errill, Edward W. (октябрь 1969). "Реология крови". Physiological Reviews . 49 (4): 863–888. doi :10.1152/physrev.1969.49.4.863. PMID  4898603. В нормальной крови при уровнях скорости сдвига, при которых применимо уравнение 15, т. е. ньютоновское течение, было показано, что температурный коэффициент вязкости идентичен таковому для воды в диапазоне 10-37°C
5. Cinar, Yildirim; Senyol, A. Mete; Duman, Kamber (май 2001 г.). «Вязкость крови и артериальное давление: роль температуры и гипергликемии». American Journal of Hypertension . 14 (5): 433–438. doi : 10.1016/S0895-7061(00)01260-7 . PMID  11368464.
6. Каро, CG; Педли, TJ; Шротер, RC; Сид, WA (1978). Механика циркуляции . Oxford University Press. стр. 3–60, 151–176. ISBN 978-0-19-263323-1.
7. Naqash, Imtiaz A.; Draboo, MA; Lone, Abdul Qayoom; Nengroo, Showkat H.; Kirmani, Altaf; Bhat, Abdul Rashid (2011). «Оценка острой нормоволемической гемодилюции и аутотрансфузии у нейрохирургических пациентов, перенесших удаление внутричерепной менингиомы». Журнал анестезиологии и клинической фармакологии . 27 (1): 54–58. doi : 10.4103/0970-9185.76645 . ISSN  0970-9185. PMC 3146160. PMID 21804707  . 
8. Сайто, Тихиро; Камей, Тетсуя; Кубота, Сёдзи; Ёсида, Киёси; Хибия, Макото; Хашимото, Сюдзи (декабрь 2018 г.). «Связь первичной гемодилюции и ретроградной аутологичной заливки с переливанием в кардиохирургии: анализ базы данных случаев перфузии Японского общества экстракорпоральных технологий в медицине». Журнал экстракорпоральных технологий . 50 (4): 231–236. doi :10.1051/ject/201850231. ISSN  0022-1058. PMC 6296452. PMID 30581230  . 
9. "Эффективность острой нормоволемической гемодилюции, оцененная как функция потерянной крови". Журнал Американского общества анестезиологов. Архивировано из оригинала 29 июня 2012 г. Получено 5 апреля 2011 г.
10. Kaya, M.; Li, JK-J. (2001). "Гемодилюция: Моделирование и клинические аспекты". Гемодилюция: Моделирование и клинические аспекты . Том 1. IEEE. С. 177–179. doi :10.1109/IEMBS.2001.1018881. ISBN 978-0-7803-7211-5. S2CID  73295413.
11. Фельдман, Джеффри М.; Рот, Джонатан В.; Бьоракер, Дэвид Г. (январь 1995 г.). «максимальная экономия крови путем острой нормоволемической гемодилюции». Анестезия и анальгезия . 80 (1): 108–113. doi : 10.1097/00000539-199501000-00019 . PMID  7802266. S2CID  24131754. Архивировано из оригинала 23 февраля 2022 г. Получено 5 апреля 2011 г.
12. Costanzo, Linda S. (2003). Физиология . Board Review Series (3-е изд.). Филадельфия: Lippincott Williams & Wilkins. стр. 73–113. ISBN 978-0781739191.
13. Кинг, Джордан; Лоури, Дэвид Р. (2022), «Физиология, сердечный выброс», StatPearls , Treasure Island (FL): StatPearls Publishing, PMID  29262215 , получено 16.05.2022
14. Насури, Алиреза; Тагипур, Али; Шахбаззаде, Делавар; Аминириссехей, Абдольхосейн; Могаддам, Шариф (2014). «Оценка места сердца и длины хвоста у Naja oxiana, Macrovipera lebetina и Montivipera latifii». Азиатско-Тихоокеанский журнал тропической медицины . 7 : S137–S142. дои : 10.1016/S1995-7645(14)60220-0 . ПМИД  25312108.
15. Лиллиуайт, Харви Б.; Альберт, Джеймс С.; Шихи, Коулман М.; Сеймур, Роджер С. (2012). «Гравитация и эволюция кардиопульмональной морфологии у змей». Сравнительная биохимия и физиология . 161 (2): 230–242. doi :10.1016/j.cbpa.2011.10.029. PMC 3242868. PMID  22079804 . 
16. Munson BR, Young DF, Okiishi TH, Huebsch WW (2009). Основы механики жидкости (шестое изд.). Нью-Джерси: John Wiley &Sons, Inc. стр. 725. ISBN 978-0-470-26284-9.
17. Фунг, Юань-чэн; Цвайфах, Б. В. (1971). «Микроциркуляция: механика кровотока в капиллярах». Annual Review of Fluid Mechanics . 3 : 189–210. Bibcode : 1971AnRFM...3..189F. doi : 10.1146/annurev.fl.03.010171.001201.
18. Tortora, Gerard J.; Derrickson, Bryan (2012). «Сердечно-сосудистая система: кровеносные сосуды и гемодинамика». Principles of Anatomy & Physiology (13-е изд.). John Wiley & Sons. стр. 816. ISBN 978-0470-56510-0.
19. Штюкер, М.; Бейлер, В.; Рейтер, Т.; Хоффман, К.; Келлам, К.; Альтмейер, П. (1996). «Скорость движения капиллярных кровяных клеток в капиллярах кожи человека, расположенных перпендикулярно поверхности кожи: измерено новым лазерным допплеровским анемометром». Microvascular Research . 52 (2): 188–192. doi :10.1006/mvre.1996.0054. PMID  8901447.
20. Tortora, Gerard J.; Derrickson, Bryan (2012). «Сердечно-сосудистая система: кровеносные сосуды и гемодинамика». Principles of Anatomy & Physiology (анализ ламинарного потока) (13-е изд.). John Wiley & Sons. стр. 817. ISBN 978-0470-56510-0.
21. Мариеб, Элейн Н.; Хен, Катя (2013). «Сердечно-сосудистая система: кровеносные сосуды». Анатомия и физиология человека (9-е изд.). Pearson Education. стр. 712. ISBN 978-0-321-74326-8.
22. GB Thurston, Вязкость и вязкоупругость крови в трубках малого диаметра, Microvasular Research 11, 133-146, 1976
23. Womersley JR (1955). «Метод расчета скорости, скорости потока и вязкого сопротивления в артериях, когда градиент давления известен». Journal of Physiology . 127 (3): 553–563. doi :10.1113/jphysiol.1955.sp005276. PMC 1365740. PMID  14368548 . 
24. Сиркар, Сабьясач (2008). Принципы медицинской физиологии . Индия: Vistasta Publishing. ISBN 978-1-58890-572-7.
25. Fung, Yuan-cheng (1997). Биомеханика:Кровообращение . Нью-Йорк: Springer. С. 571. ISBN 978-0-387-94384-8.
26. Розенсон RS, Вольф Д, Грин Д, Босс AH, Кенси KR (февраль 2004 г.). «Аспирин. Аспирин не изменяет собственную вязкость крови». J. Thromb. Haemost . 2 (2): 340–341. doi : 10.1111/j.1538-79333.2004.0615f.x . PMID  14996003.
27. Delong, Claire; Sharma, Sandeep (2022), "Физиология, периферическое сосудистое сопротивление", StatPearls , Treasure Island (FL): StatPearls Publishing, PMID  30855892 , получено 16.05.2022
28. Надери, Насим (2022-01-01), Малеки, Маджид; Ализадехасл, Азин; Хагджу, Маджид (ред.), «Глава 11 — Гемодинамическое исследование», Практическая кардиология (второе издание) , Elsevier, стр. 201–216, ISBN 978-0-323-80915-3, получено 2022-05-22
29. Поттерс (13 февраля 2014 г.). «Измерение напряжения сдвига стенки с помощью МРТ с кодированием скорости». Current Cardiovascular Imaging Reports . 7 (4). doi :10.1007/s12410-014-9257-1. S2CID  55721300.
30. Tazraei, P.; Riasi, A.; Takabi, B. (2015). «Влияние неньютоновских свойств крови на кровяной молот через заднюю мозговую артерию». Mathematical Biosciences . 264 : 119–127. doi :10.1016/j.mbs.2015.03.013. PMID  25865933.
31. Лоу, Мэри (2015-04-15). Гемодинамический мониторинг: развивающиеся технологии и клиническая практика (1-е изд.). Сент-Луис, Миссури: Elsevier Mosby. стр. 25. ISBN 978-0-323-08512-0.
32. Caro, Colin G. (1978). Механика циркуляции . Оксфорд [Оксфордшир]: Oxford University Press. ISBN 978-0-19-263323-1.
33. "Нормальный диапазон артериального давления у взрослых". Здоровье и жизнь. 2010-06-07. Архивировано из оригинала 2016-03-18 . Получено 2016-02-06 .
34. Демерс, Дэниел; Вакс, Далия (2022), «Физиология, среднее артериальное давление», StatPearls , Treasure Island (FL): StatPearls Publishing, PMID  30855814 , получено 22.05.2022
35. Клабунде, Ричард (2005). Концепции сердечно-сосудистой физиологии . Липпинкотт Уильямс и Уилкинс. стр. 93–94. ISBN 978-0-7817-5030-1.
36. Markham LW, Knecht SK, Daniels SR, Mays WA, Khoury PR, Knilans TK (ноябрь 2004 г.). «Развитие градиента артериального давления между руками и ногами, вызванного физическими упражнениями, и аномальная податливость артерий у пациентов с восстановленной коарктацией аорты». Am. J. Cardiol . 94 (9): 1200–1202. doi :10.1016/j.amjcard.2004.07.097. PMID  15518624.
37. "RHC | Медицинский центр Университета Вандербильта". medsites.vumc.org . Получено 16.05.2022 .
38. Puyo, L., M. Paques, M. Fink, JA. Sahel и M. Atlan. «In vivo лазерная допплеровская голография сетчатки человека». Biomedical optics express 9, № 9 (2018): 4113-4129.
39. Пуйо, Лео, Мишель Пакес, Матиас Финк, Хосе-Ален Сахель и Майкл Атлан. «Анализ формы волны кровотока в сетчатке и хориоидеи человека с помощью лазерной допплеровской голографии». Biomedical Optics Express 10, № 10 (2019): 4942-4963.
40. "haemodynamic". Lexico UK English Dictionary . Oxford University Press . Архивировано из оригинала 2020-03-22.

Библиография

• Берн Р.М., Леви М.Н. Физиология сердечно-сосудистой системы. 7-е изд. Мосби 1997 г.
• Роуэлл Л. Б. Управление сердечно-сосудистой системой человека. Oxford University Press, 1993.
• Браунвальд Э. (редактор). Болезни сердца: учебник по сердечно-сосудистой медицине. 5-е изд. WBSaunders 1997
• Siderman S, Beyar R, Kleber AG. Электрофизиология сердца, кровообращение и транспорт. Kluwer Academic Publishers 1991
• Американская кардиологическая ассоциация
• Отто CM, Стоддард M, Ваггонер A, Зогби WA. Рекомендации по количественной оценке допплеровской эхокардиографии: отчет целевой группы по количественной оценке допплеровской эхокардиографии Комитета по номенклатуре и стандартам Американского общества эхокардиографии. J Am Soc Echocardiogr 2002;15:167-184
• Петерсон Л. Х., Динамика пульсирующего кровотока, Circ. Res. 1954;2;127-139
• Гемодинамический мониторинг, Bigatello LM, George E., Minerva Anestesiol, 2002 Апрель;68(4):219-25
• Клод Франчески Исследование сосудов с помощью ультразвуковой допплерографии Массона, 1979 ISBN Nr 2-225-63679-6
• Клод Франчески; Паоло Замбони Принципы венозной гемодинамики Nova Science Publishers 2009-01 ISBN Nr 1606924850/9781606924853
• Клод Франчески Венозная недостаточность таза и нижних конечностей — гемодинамическое обоснование
• WR Milnor: Гемодинамика, Williams & Wilkins, 1982
• Б. Бо Срамек: Системная гемодинамика и гемодинамическое управление, 4-е издание, ESBN 1-59196-046-0

Внешние ссылки

• Изучите гемодинамику