
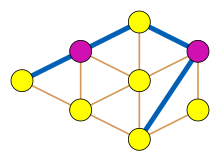
В теории графов , области математики, граф без клешней — это граф, который не имеет клешни в качестве индуцированного подграфа .
Клешня — это другое название полного двудольного графа K 1,3 (то есть графа-звезды, состоящего из трех ребер, трех листьев и центральной вершины). Граф без клешней — это граф, в котором ни один индуцированный подграф не является клешней; то есть любое подмножество из четырех вершин имеет не только три ребра, соединяющие их в этом шаблоне. Эквивалентно, граф без клешней — это граф, в котором окрестность любой вершины является дополнением графа без треугольников .
Графы без клешней изначально изучались как обобщение линейных графов и получили дополнительную мотивацию благодаря трем ключевым открытиям о них: тот факт, что все связные графы без клешней четного порядка имеют совершенные паросочетания , открытие алгоритмов полиномиального времени для поиска максимальных независимых множеств в графах без клешней и характеристика совершенных графов без клешней . [1] Они являются предметом сотен математических исследовательских работ и нескольких обзоров. [1]

Легко проверить, что заданный граф с n вершинами и m ребрами свободен от клешней за время O( n 4 ), проверяя каждый кортеж из 4 вершин, чтобы определить, порождают ли они клешню. [6] С большей эффективностью и большей сложностью можно проверить, свободен ли граф от клешней, проверив для каждой вершины графа, что дополнительный граф его соседей не содержит треугольника. Граф содержит треугольник тогда и только тогда, когда куб его матрицы смежности содержит ненулевой диагональный элемент, поэтому нахождение треугольника может быть выполнено за то же асимптотическое время, что и умножение матриц n × n . [7] Следовательно, при использовании алгоритма Копперсмита–Винограда общее время для этого алгоритма распознавания без клешней будет O( n 3.376 ).
Клокс, Кратч и Мюллер (2000) наблюдают, что в любом графе без клешней каждая вершина имеет не более 2 √ m соседей; в противном случае по теореме Турана у соседей вершины не было бы достаточно оставшихся ребер, чтобы сформировать дополнение графа без треугольников. Это наблюдение позволяет выполнить проверку каждого соседства в быстром алгоритме на основе умножения матриц, описанном выше, за то же асимптотическое время, что и умножение матриц 2 √ m × 2 √ m , или быстрее для вершин с еще более низкими степенями. Худший случай для этого алгоритма возникает, когда Ω( √ m ) вершин имеют Ω( √ m ) соседей каждая, а оставшиеся вершины имеют мало соседей, поэтому его общее время составляет O( m 3.376/2 ) = O( m 1.688 ).
Поскольку графы без клешней включают дополнения графов без треугольников, число графов без клешней на n вершинах растет по крайней мере так же быстро, как число графов без треугольников, экспоненциально в квадрате n . Число связанных графов без клешней на n узлах для n = 1, 2, ... равно
Если графы могут быть несвязными, то число графов становится еще больше: они
Метод Палмера, Рида и Робинсона (2002) позволяет очень эффективно подсчитывать количество кубических графов без клешней, что необычно для задач перечисления графов .

Самнер (1974) и, независимо, Лас-Верньяс (1975) доказали, что любой связный граф без клешней с четным числом вершин имеет идеальное паросочетание . [8] То есть, существует набор ребер в графе, такой что каждая вершина является конечной точкой ровно одного из сопоставленных ребер. Частный случай этого результата для линейных графов подразумевает, что в любом графе с четным числом ребер можно разбить ребра на пути длины два. Совершенные паросочетания могут быть использованы для предоставления другой характеристики графов без клешней: это в точности графы, в которых каждый связный индуцированный подграф четного порядка имеет идеальное паросочетание. [8]
Доказательство Самнера показывает, более строго, что в любом связном графе без клешней можно найти пару смежных вершин, удаление которых оставляет оставшийся граф связным. Чтобы показать это, Самнер находит пару вершин u и v , которые находятся максимально далеко друг от друга в графе, и выбирает w в качестве соседа v , который находится максимально далеко от u ; как он показывает, ни v, ни w не могут лежать на каком-либо кратчайшем пути от любого другого узла до u , поэтому удаление v и w оставляет оставшийся граф связным. Многократное удаление сопоставленных пар вершин таким образом образует идеальное паросочетание в заданном графе без клешней.
Та же идея доказательства справедлива в более общем случае, если u — любая вершина, v — любая вершина, максимально удаленная от u , а w — любой сосед v , максимально удаленный от u . Кроме того, удаление v и w из графа не изменяет никаких других расстояний от u . Следовательно, процесс формирования соответствия путем поиска и удаления пар vw , максимально удаленных от u, может быть выполнен одним обходом в обратном порядке дерева поиска в ширину графа с корнем в u за линейное время. Chrobak, Naor & Novick (1989) предлагают альтернативный алгоритм линейного времени, основанный на поиске в глубину , а также эффективные параллельные алгоритмы для той же задачи.
Faudree, Flandrin & Ryjáček (1997) перечисляют несколько связанных результатов, включая следующие: ( r − 1)-связные K 1, r -свободные графы четного порядка имеют совершенные паросочетания для любого r ≥ 2; графы без клешней нечетного порядка с не более чем одной вершиной степени один могут быть разбиты на нечетный цикл и паросочетание; для любого k , которое не превышает половины минимальной степени графа без клешней, в котором либо k , либо число вершин четно, граф имеет k -фактор; и, если граф без клешней является (2 k + 1)-связным, то любое k -реберное паросочетание может быть расширено до совершенного паросочетания.
Независимое множество в линейном графе соответствует сопоставлению в его базовом графе, множеству ребер, никакие два из которых не имеют общей конечной точки. Алгоритм цветения Эдмондса (1965) находит максимальное сопоставление в любом графе за полиномиальное время, что эквивалентно вычислению максимального независимого множества в линейном графе. Это было независимо расширено до алгоритма для всех графов без клешней Сбихи (1980) и Минти (1980). [9]
Оба подхода используют наблюдение, что в графах без клешней ни одна вершина не может иметь более двух соседей в независимом множестве, и поэтому симметрическая разность двух независимых множеств должна индуцировать подграф степени не более двух; то есть это объединение путей и циклов. В частности, если I является немаксимальным независимым множеством, оно отличается от любого максимального независимого множества четными циклами и так называемыми увеличивающими путями : индуцируемыми путями , которые чередуются между вершинами не из I и вершинами из I , и для которых обе конечные точки имеют только одного соседа в I . Поскольку симметрическая разность I с любым увеличивающим путем дает большее независимое множество, задача, таким образом, сводится к поиску увеличивающих путей до тех пор, пока больше не будет найдено, аналогично алгоритмам для поиска максимальных паросочетаний.
Алгоритм Сбихи воссоздает шаг сокращения цветка алгоритма Эдмондса и добавляет похожий, но более сложный шаг сокращения клики . Подход Минти заключается в преобразовании экземпляра проблемы во вспомогательный линейный граф и непосредственном использовании алгоритма Эдмондса для поиска увеличивающихся путей. После исправления Накамуры и Тамуры 2001 года результат Минти также может быть использован для решения за полиномиальное время более общей задачи нахождения в графах без клешней независимого множества максимального веса. Известны также обобщения этих результатов на более широкие классы графов. [9] Показав новую структурную теорему, Фаэнца, Ориоло и Штауффер (2011) дали алгоритм кубического времени, который также работает в весовой настройке.
Совершенный граф — это граф, в котором хроматическое число и размер максимальной клики равны, и в котором это равенство сохраняется в каждом индуцированном подграфе. Теперь известно ( сильная теорема о совершенном графе ), что совершенные графы можно охарактеризовать как графы, которые не имеют в качестве индуцированных подграфов ни нечетного цикла, ни дополнения нечетного цикла (так называемой нечетной дыры ). [10] Однако в течение многих лет это оставалось нерешенной гипотезой, доказанной только для специальных подклассов графов. Одним из таких подклассов было семейство графов без клешней: несколькими авторами было обнаружено, что графы без клешней без нечетных циклов и нечетных дыр являются совершенными. Совершенные графы без клешней можно распознать за полиномиальное время. В совершенном графе без клешней окрестность любой вершины образует дополнение двудольного графа . Можно раскрасить совершенные графы без клешней или найти в них максимальные клики за полиномиальное время. [11]
В общем случае, NP-трудно найти самую большую клику в графе без клешней. [12] Также NP-трудно найти оптимальную раскраску графа, потому что (с помощью линейных графов) эта задача обобщает NP-трудную задачу вычисления хроматического индекса графа. [6] По той же причине NP-трудно найти раскраску, которая достигает коэффициента аппроксимации лучше, чем 4/3. Однако коэффициент аппроксимации два может быть достигнут с помощью жадного алгоритма раскраски, потому что хроматическое число графа без клешней больше половины его максимальной степени. Обобщение гипотезы о раскраске списка ребер гласит, что для графов без клешней хроматическое число списка равно хроматическому числу; эти два числа могут быть далеко друг от друга в других видах графов. [13]
Графы без клешней являются χ -ограниченными , что означает, что любой граф без клешней с большим хроматическим числом содержит большую клику. Более того, из теоремы Рамсея следует , что любой граф без клешней с большой максимальной степенью содержит большую клику, размер которой примерно пропорционален квадратному корню степени. Для связных графов без клешней, которые включают по крайней мере одно независимое множество из трех вершин, возможна более сильная связь между хроматическим числом и размером клики: в этих графах существует клика размером по крайней мере в половину хроматического числа. [14]
Хотя не каждый граф без клешней является совершенным, графы без клешней удовлетворяют другому свойству, связанному с совершенством. Граф называется совершенным доминированием , если он имеет минимальное доминирующее множество , которое является независимым, и если то же свойство выполняется во всех его индуцированных подграфах. Графы без клешней обладают этим свойством. Чтобы увидеть это, пусть D будет доминирующим множеством в графе без клешней, и предположим, что v и w являются двумя смежными вершинами в D ; тогда множество вершин, доминируемых v , но не w, должно быть кликой (иначе v была бы центром клешни). Если каждая вершина в этой клике уже доминируется по крайней мере одним другим членом D , то v можно удалить, создав меньшее независимое доминирующее множество, а в противном случае v можно заменить одной из недоминируемых вершин в ее клике, создав доминирующее множество с меньшим количеством смежностей. Повторяя этот процесс замены, в конечном итоге достигается доминирующий набор, не превышающий D , поэтому, в частности, когда начальный набор D является минимальным доминирующим набором, этот процесс формирует столь же малый независимый доминирующий набор. [15]
Несмотря на это свойство доминирования, определить размер минимального доминирующего множества в графе без клешней является NP-трудной задачей. [6] Однако, в отличие от ситуации для более общих классов графов, нахождение минимального доминирующего множества или минимального связного доминирующего множества в графе без клешней является фиксированно-параметрически решаемой задачей : ее можно решить за время, ограниченное полиномом от размера графа, умноженным на экспоненциальную функцию размера доминирующего множества. [16]
Чудновский и Сеймур (2005) рассматривают серию статей, в которых они доказывают структурную теорию для графов без клешней, аналогичную теореме о структуре графа для семейств графов с замкнутыми минорами, доказанной Робертсоном и Сеймуром, и структурной теории для совершенных графов, которую Чудновский, Сеймур и их соавторы использовали для доказательства сильной теоремы о совершенных графах. [10] Теория слишком сложна, чтобы подробно описывать ее здесь, но чтобы дать представление о ней, достаточно описать два их результата. Во-первых, для специального подкласса графов без клешней, которые они называют квазилинейными графами (эквивалентно, локально ко-двудольными графами), они утверждают, что каждый такой граф имеет одну из двух форм:
Чудновский и Сеймур классифицируют произвольные связные графы без клешней одним из следующих способов:
Большая часть работы в их структурной теории включает в себя дальнейший анализ антипризматических графов. Граф Шлефли , сильно регулярный граф без клешней с параметрами srg(27,16,10,8), играет важную роль в этой части анализа. Эта структурная теория привела к новым достижениям в полиэдральной комбинаторике и новым границам хроматического числа графов без клешней, [5] [17], а также к новым алгоритмам с фиксированными параметрами для доминирующих множеств в графах без клешней. [18]
{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ).