
Математические диаграммы , такие как графики и диаграммы , в основном предназначены для передачи математических отношений, например, сравнений во времени. [1]

Комплексное число можно визуально представить в виде пары чисел, образующих вектор на диаграмме, называемой диаграммой Аргана . Комплексную плоскость иногда называют плоскостью Аргана , поскольку она используется в диаграммах Аргана . Они названы в честь Жана-Робера Аргана (1768–1822), хотя впервые были описаны норвежско-датским землемером и математиком Каспаром Весселем (1745–1818). [2] Диаграммы Аргана часто используются для построения графика положений полюсов и нулей функции на комплексной плоскости.
Концепция комплексной плоскости допускает геометрическую интерпретацию комплексных чисел. При сложении они складывают подобные векторы . Умножение двух комплексных чисел проще всего выразить в полярных координатах — величина или модуль произведения является произведением двух абсолютных значений , или модулей, а угол или аргумент произведения является суммой двух углов, или аргументов. В частности, умножение на комплексное число с модулем 1 действует как поворот.
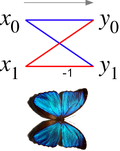
В контексте алгоритмов быстрого преобразования Фурье бабочка — это часть вычисления, которая объединяет результаты меньших дискретных преобразований Фурье (ДПФ) в большее ДПФ или наоборот (разбивая большее ДПФ на подпреобразования). Название «бабочка» происходит от формы диаграммы потока данных в случае с основанием 2, как описано ниже. Такую же структуру можно найти в алгоритме Витерби , используемом для поиска наиболее вероятной последовательности скрытых состояний.
Диаграмма бабочки показывает диаграмму потока данных, соединяющую входы x (слева) с выходами y , которые зависят от них (справа) для шага «бабочки» алгоритма Кули–Тьюки FFT по основанию 2. Эта диаграмма напоминает бабочку , как в бабочке Морфо, показанной для сравнения, отсюда и название.

В математике, и особенно в теории категорий , коммутативная диаграмма — это диаграмма объектов , также известных как вершины, и морфизмов , также известных как стрелки или ребра, такая, что при выборе двух объектов любой направленный путь через диаграмму приводит к одному и тому же результату по композиции.
Коммутативные диаграммы играют в теории категорий ту же роль, что и уравнения в алгебре.

Диаграмма Хассе — это простое изображение конечного частично упорядоченного множества , образующее рисунок транзитивного сокращения частичного порядка . Конкретно, каждый элемент множества представляется как вершина на странице и рисуется отрезок прямой или кривая, которая идет вверх от x к y точно тогда, когда x < y и нет z такого, что x < z < y . В этом случае мы говорим, что y покрывает x, или y является непосредственным последователем x. В диаграмме Хассе требуется, чтобы кривые были нарисованы так, чтобы каждая встречала ровно две вершины: свои две конечные точки. Любая такая диаграмма (при условии, что вершины помечены) однозначно определяет частичный порядок, и любой частичный порядок имеет уникальное транзитивное сокращение, но существует множество возможных размещений элементов на плоскости, что приводит к различным диаграммам Хассе для данного порядка, которые могут иметь сильно различающийся внешний вид.

В теории узлов полезным способом визуализации и манипулирования узлами является проецирование узла на плоскость — представьте, что узел отбрасывает тень на стену. Небольшое возмущение в выборе проекции гарантирует, что она будет один к одному, за исключением двойных точек, называемых пересечениями , где «тень» узла пересекает себя один раз поперечно [3]
На каждом пересечении мы должны указать, какая часть «над», а какая «под», чтобы иметь возможность воссоздать исходный узел. Это часто делается путем создания разрыва в нити, идущей снизу. Если, следуя диаграмме, узел попеременно пересекает себя «над» и «под», то диаграмма представляет собой особенно хорошо изученный класс узлов, чередующиеся узлы .

Диаграмма Венна — это представление математических множеств: математическая диаграмма, представляющая множества в виде кругов, причем их отношения друг к другу выражаются через их перекрывающиеся положения, так что показаны все возможные отношения между множествами. [4]
Диаграмма Венна строится с помощью набора простых замкнутых кривых, нарисованных на плоскости. Принцип этих диаграмм заключается в том, что классы должны быть представлены областями в таком отношении друг к другу, что все возможные логические отношения этих классов могут быть указаны на одной и той же диаграмме. То есть, диаграмма изначально оставляет место для любого возможного отношения классов, а фактическое или заданное отношение затем может быть указано путем указания того, что некоторая конкретная область является нулевой или не является нулевой. [5]

Диаграмма Вороного — это особый вид разложения метрического пространства , определяемый расстояниями до заданного дискретного набора объектов в пространстве, например, дискретным набором точек. Эта диаграмма названа в честь Георгия Вороного , также называется мозаикой Вороного , разложением Вороного или мозаикой Дирихле в честь Петера Густава Лежена Дирихле .
В простейшем случае нам дан набор точек S на плоскости, которые являются узлами Вороного. Каждый узел s имеет ячейку Вороного V(s), состоящую из всех точек, которые ближе к s, чем к любому другому узлу. Сегменты диаграммы Вороного — это все точки на плоскости, которые равноудалены от двух узлов. Узлы Вороного — это точки, равноудаленные от трех (или более) узлов

Группа обоев или группа симметрии плоскости или кристаллографическая группа плоскости — это математическая классификация двумерного повторяющегося узора, основанная на симметриях в узоре. Такие узоры часто встречаются в архитектуре и декоративном искусстве. Существует 17 возможных различных групп .
Группы обоев — это двумерные группы симметрии , промежуточные по сложности между более простыми группами фриза и трехмерными кристаллографическими группами , также называемыми пространственными группами . Группы обоев классифицируют узоры по их симметрии. Незначительные различия могут помещать похожие узоры в разные группы, в то время как узоры, которые сильно различаются по стилю, цвету, масштабу или ориентации, могут принадлежать к одной и той же группе.
Диаграмма Юнга или таблица Юнга , также называемая диаграммой Феррерса , представляет собой конечный набор блоков или ячеек, расположенных в выровненных по левому краю строках, при этом размеры строк слабо уменьшаются (каждая строка имеет такую же или меньшую длину, чем предыдущая).

Перечисление количества ящиков в каждой строке дает разбиение положительного целого числа n , общего количества ящиков диаграммы. Говорят, что диаграмма Юнга имеет форму , и она несет ту же информацию, что и это разбиение. Перечисление количества ящиков в каждом столбце дает другое разбиение, сопряженное или транспонированное разбиение ; можно получить диаграмму Юнга этой формы, отразив исходную диаграмму вдоль ее главной диагонали.
Таблицы Юнга были введены Альфредом Юнгом , математиком из Кембриджского университета , в 1900 году. Затем они были применены к изучению симметрической группы Георгом Фробениусом в 1903 году. Их теория была в дальнейшем развита многими математиками.