Логическое двуусловие

Понятие в логике и математике

Диаграмма Венна ( истинная часть выделена красным) ${\displaystyle P\leftrightarrow Q}$

В логике и математике логическое бикондиционал , также известное как материальное бикондиционал , или эквивалентность , или би-импликация , или двойная импликация , представляет собой логическую связку , используемую для соединения двух утверждений и формирования утверждения « тогда и только тогда, когда » (часто сокращается как « если и только если » ^{[1] ]} ), где называется антецедентом и консеквентом . ^{[2] [3]} ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$

В настоящее время обозначения эквивалентности включают . ${\displaystyle \leftrightarrow ,\Leftrightarrow ,\equiv }$

${\displaystyle P\leftrightarrow Q}$логически эквивалентен обоим и , а также логическому оператору XNOR (исключающее ни) , что означает «оба или ничего». ${\displaystyle (P\rightarrow Q)\land (Q\rightarrow P)}$ ${\displaystyle (P\land Q)\lor (\neg P\land \neg Q)}$

С семантической точки зрения единственный случай, когда логическое бикондиционал отличается от материального кондиционала, — это случай, когда гипотеза (антецедент) ложна, но вывод (следствие) истинен. В этом случае результат истинен для условного выражения, но ложен для двуусловного. ^[2]

В концептуальной интерпретации P = Q означает «Все P являются Q и все Q являются P ». Другими словами, множества P и Q совпадают: они идентичны. Однако это не означает, что P и Q должны иметь одно и то же значение (например, P может быть «равноугольным трехсторонним», а Q может быть «равносторонним треугольником»). Когда оно сформулировано в виде предложения, антецедент является подлежащим , а консеквент — предикатом универсального утвердительного суждения (например, во фразе «все люди смертны», «люди» — это подлежащее, а «смертный» — это предикат).

В пропозициональной интерпретации означает, что P подразумевает Q , а Q подразумевает P ; другими словами, предложения логически эквивалентны в том смысле, что оба либо совместно истинны, либо совместно ложны. Опять же, это не означает, что они должны иметь одинаковое значение, поскольку P может означать «треугольник ABC имеет две равные стороны», а Q может быть «треугольник ABC имеет два равных угла». В общем, антецедент — это предпосылка или причина , а следствие — это следствие . Когда импликация переводится посредством гипотетического (или условного ) суждения, антецедент называется гипотезой (или условием ), а консеквент называется тезисом . ${\displaystyle P\leftrightarrow Q}$

Распространенным способом демонстрации бикондиционала формы является демонстрация этого и отдельно (из-за его эквивалентности соединению двух обратных кондиционалов ^[2] ). Еще один способ продемонстрировать то же самое бикондиционал — продемонстрировать, что и . ${\displaystyle P\leftrightarrow Q}$ ${\displaystyle P\rightarrow Q}$ ${\displaystyle Q\rightarrow P}$ ${\displaystyle P\rightarrow Q}$ ${\displaystyle \neg P\rightarrow \neg Q}$

Когда оба члена бикондиционала являются предложениями, его можно разделить на два кондиционала, один из которых называется теоремой, а другой — обратным ему . ^{[ нужна цитата ]} Таким образом, всякий раз, когда теорема и обратное ей утверждение верны, у нас есть двустороннее условие. Простая теорема порождает импликацию, антецедентом которой является гипотеза , а следствием — тезис теоремы.

Часто говорят, что гипотеза является достаточным условием тезиса, а тезис — необходимым условием гипотезы. То есть достаточно, чтобы гипотеза была верной, чтобы тезис был истинным, в то время как необходимо, чтобы тезис был истинным, если бы гипотеза была верной. Когда теорема и обратное ей утверждение истинны, ее гипотеза называется необходимым и достаточным условием тезиса. То есть гипотеза является одновременно и причиной, и следствием тезиса.

Обозначения

Обозначения для обозначения эквивалентности, используемые в истории, включают:

• ${\displaystyle =}$у Джорджа Буля в 1847 году. ^[4] Хотя Буль использовал главным образом классы, он также рассмотрел случай, когда предложения в , и в то время являются эквивалентностью. ${\displaystyle =}$ ${\displaystyle x,y}$ ${\displaystyle x=y}$ ${\displaystyle =}$
• ${\displaystyle \equiv }$во Фреге в 1879 году; ^[5]
• ${\displaystyle \sim }$в Бернейсе в 1918 году; ^[6]
• ${\displaystyle \rightleftarrows }$у Гильберта в 1927 г. (пока он использован в качестве основного символа в статье); ^[7] ${\displaystyle \sim }$
• ${\displaystyle \leftrightarrow }$у Гильберта и Аккермана в 1928 году ^[8] (они также введены , хотя и используются в качестве основного символа во всей книге; принят многими последователями, такими как Беккер в 1933 году ^[9] ); ${\displaystyle \rightleftarrows ,\sim }$ ${\displaystyle \sim }$ ${\displaystyle \leftrightarrow }$
• ${\displaystyle E}$(префикс) у Лукасевича в 1929 г. ^[10] и (префикс) у Лукасевича в 1951 г.; ^[11] ${\displaystyle Q}$
• ${\displaystyle \supset \subset }$в Хейтинге в 1930 году; ^[12]
• ${\displaystyle \Leftrightarrow }$в Бурбаки в 1954 году; ^[13]
• ${\displaystyle \subset \supset }$в Чазале в 1996 году; ^[14]

и так далее. Кто-то еще также использует или время от времени. ^{[ нужна ссылка ] [ неопределенно ] [ нужны разъяснения ]} ${\displaystyle \operatorname {EQ} }$ ${\displaystyle \operatorname {EQV} }$

Определение

Логическое равенство (также известное как двуусловное) — это операция над двумя логическими значениями , обычно значениями двух высказываний , которая дает значение true тогда и только тогда, когда оба операнда ложны или оба операнда истинны. ^[2]

Таблица истинности

Ниже представлена ​​таблица истинности для : ${\displaystyle P\leftrightarrow Q}$

Если задействовано более двух утверждений, их объединение может быть неоднозначным. Например, заявление ${\displaystyle \leftrightarrow }$

${\displaystyle x_{1}\leftrightarrow x_{2}\leftrightarrow x_{3}\leftrightarrow \cdots \leftrightarrow x_{n}}$

может быть истолковано как

${\displaystyle (((x_{1}\leftrightarrow x_{2})\leftrightarrow x_{3})\leftrightarrow \cdots )\leftrightarrow x_{n}}$,

или может быть истолковано как утверждение, что все x _i совместно истинны или совместно ложны :

${\displaystyle (x_{1}\land \cdots \land x_{n})\lor (\neg x_{1}\land \cdots \land \neg x_{n})}$

Как выяснилось, эти два утверждения одинаковы только тогда, когда задействовано ноль или два аргумента. Фактически, следующие таблицы истинности показывают один и тот же битовый шаблон только в строке без аргумента и в строках с двумя аргументами:

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
означает эквивалент центральной диаграммы Венна ниже, а линия (ABC) в этой матрице представляет одну и ту же операцию.
${\displaystyle \neg ~(\neg x_{1}\oplus \cdots \oplus \neg x_{n})}$

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
означает сокращение диаграммы Венна, расположенной непосредственно ниже, а линия (ABC) в этой матрице представляет одну и ту же операцию.
${\displaystyle (~x_{1}\land \cdots \land x_{n}~)}$
${\displaystyle \lor ~(\neg x_{1}\land \cdots \land \neg x_{n})}$

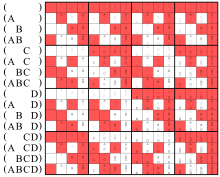
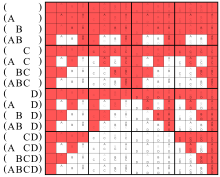
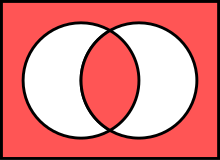
Левая диаграмма Венна ниже и линии (AB) в этих матрицах представляют одну и ту же операцию.

Диаграммы Венна

Красные области означают истину (как вдля и ).

Характеристики

Коммутативность : Да

Ассоциативность : Да

Дистрибутивность : биусловное выражение не распространяется ни на одну двоичную функцию (даже на себя), но логическая дизъюнкция распространяется на биусловное выражение.

Идемпотентность : Нет

Монотонность : Нет

Сохранение истины: Да.
Когда все входные данные верны, выходные данные верны.

Сохранение ложности: Нет.
Когда все входные данные ложны, выходные данные не являются ложными.

Спектр Уолша : (2,0,0,2)

Нелинейность : 0 (функция линейна)

Правила вывода

Как и все связки в логике первого порядка, бикондиционал имеет правила вывода, которые управляют его использованием в формальных доказательствах.

Двуусловное введение

Двуусловное введение позволяет сделать вывод, что если B следует из A, а A следует из B, то A тогда и только тогда, когда B.

Например, из утверждений «если я дышу, то я жив» и «если я жив, то я дышу» можно сделать вывод, что «я дышу тогда и только тогда, когда я Я жив» или, что то же самое, «Я жив тогда и только тогда, когда я дышу». Или более схематично:

Б → А    А → Б    ∴ А ↔ Б

Б → А    А → Б    ∴ Б ↔ А

Двуусловное исключение

Двуусловное исключение позволяет вывести условное выражение из двуусловного: если A ↔ B истинно, то можно сделать вывод либо A → B, либо B → A.

Например, если верно, что я дышу тогда и только тогда , когда я жив, то верно и то, что если я дышу, то я жив; точно так же верно и то, что если я жив, то я дышу. Или более схематично:

 А ↔ Б   ∴ А → Б

 А ↔ Б   ∴ Б → А

Разговорное употребление

Один однозначный способ выразить бикондиционал на простом английском языке — это принять форму « b if a и a if b » — если не используется стандартная форма « a if and only if b ». Несколько более формально можно было бы также сказать, что « b подразумевает а , а а подразумевает b », или « а необходимо и достаточно для b ». Простое английское «if» иногда может использоваться как двустороннее условие (особенно в контексте математического определения ^[15] ). В этом случае при интерпретации этих слов необходимо учитывать окружающий контекст.

Например, утверждение «Я куплю вам новый кошелек, если он вам понадобится» может быть интерпретировано как двустороннее условие, поскольку говорящий не предполагает, что покупка кошелька будет действительным результатом независимо от того, нужен он или нет (так как в условном). Однако фраза «облачно, если идет дождь» обычно не подразумевается как двустороннее условие, поскольку облачно все равно может быть, даже если дождя нет.

Смотрите также

• Философский портал
• Психологический портал

• Если и только если
• Логическая эквивалентность
• Логическое равенство
• XNOR-ворота
• Двуусловное исключение
• Двуусловное введение

Рекомендации

1. Вайсштейн, Эрик В. «Если». mathworld.wolfram.com . Проверено 25 ноября 2019 г.
2. Пейл, Тимоти. «Кондиционалы и бикондиционалы». web.mnstate.edu . Архивировано из оригинала 24 октября 2020 г. Проверено 25 ноября 2019 г.
3. Бреннан, Джозеф Г. (1961). Справочник по логике (2-е изд.). Харпер и Роу. п. 81.
4. Буль, Г. (1847). Математический анализ логики как очерк дедуктивного рассуждения. Кембридж/Лондон: Макмиллан, Барклай и Макмиллан/Джордж Белл. п. 17.
5. Фреге, Г. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (на немецком языке). Halle a/S: Verlag von Louis Nebert. п. 15.
6. Бернейс, П. (1918). Beiträge zur axiomatischen Behandlung des Logik-Kalküls . Геттинген: Университет Геттингена. п. 3.
7. Гильберт, Д. (1928) [1927]. «Основы математики». Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität (на немецком языке). 6 : 65–85. дои : 10.1007/BF02940602.
8. Гильберт, Д.; Акерманн, В. (1928). Grundzügen der theoretischen Logik (на немецком языке) (1-е изд.). Берлин: Verlag фон Юлиус Шпрингер. п. 4.
9. Беккер, А. (1933). Die Aristotelische Theorie der Möglichkeitsschlösse: Eine logisch-philologische Untersuchung der Kapitel 13-22 von Aristoteles' Analytica Priora I (на немецком языке). Берлин: Junker und Dünnhaupt Verlag. п. 4.
10. Лукасевич, Дж. (1958) [1929]. Слупецкий, Дж. (ред.). Elementy logiki matematycznej (на польском языке) (2-е изд.). Варшава: Państwowe Wydawnictwo Naukowe.
11. Лукасевич, Дж. (1957) [1951]. Слупецкий, Дж. (ред.). Силлогистика Аристотеля с точки зрения современной формальной логики (на польском языке) (2-е изд.). Глазго, Нью-Йорк, Торонто, Мельбурн, Веллингтон, Бомбей, Калькутта, Мадрас, Карачи, Лахор, Дакка, Кейптаун, Солсбери, Найроби, Ибадан, Аккра, Куала-Лумпур и Гонконг: Издательство Оксфордского университета.
12. Хейтинг, А. (1930). «Формальное правило интуиционистской логики». Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse (на немецком языке): 42–56.
13. Бурбаки, Н. (1954). Теория ансамблей (на французском языке). Париж: Hermann & Cie, Éditeurs. п. 32.
14. Чазал, Г. (1996). Элементы формальной логики . Париж: Научные публикации Гермеса.
15. Фактически, именно такой стиль принят в руководстве Википедии по стилю в математике .

Внешние ссылки

• СМИ, связанные с логическим бикондиционалом, на Викискладе?

Эта статья включает в себя материал из Biconditional на PlanetMath , который доступен под лицензией Creative Commons Attribution/Share-Alike License .