Диаграмма Дынкина

В математической области теории Ли диаграмма Дынкина , названная в честь Евгения Дынкина , представляет собой тип графа с некоторыми ребрами, удвоенными или утроенными (изображаемыми в виде двойной или тройной линии). Диаграммы Дынкина возникают при классификации полупростых алгебр Ли над алгебраически замкнутыми полями , при классификации групп Вейля и других конечных групп отражений , а также в других контекстах. Различные свойства диаграммы Дынкина (например, содержит ли она кратные ребра или ее симметрии) соответствуют важным особенностям ассоциированной алгебры Ли.

Термин «диаграмма Дынкина» может быть неоднозначным. В некоторых случаях диаграммы Дынкина предполагаются направленными , в этом случае они соответствуют корневым системам и полупростым алгебрам Ли, в то время как в других случаях они предполагаются ненаправленными , в этом случае они соответствуют группам Вейля. В этой статье «диаграмма Дынкина» означает направленную диаграмму Дынкина, а ненаправленные диаграммы Дынкина будут явно так называться.

Классификация полупростых алгебр Ли

Основной интерес к диаграммам Дынкина заключается в том, что они классифицируют полупростые алгебры Ли над алгебраически замкнутыми полями . Такие алгебры Ли классифицируются через их корневую систему , которая может быть представлена диаграммой Дынкина. Затем диаграммы Дынкина классифицируются в соответствии с ограничениями, которым они должны удовлетворять, как описано ниже.

Отбрасывание направления на ребрах графа соответствует замене корневой системы конечной группой отражений , которую она порождает, так называемой группой Вейля , и, таким образом, неориентированные диаграммы Дынкина классифицируют группы Вейля.

Они имеют следующее соответствие для алгебр Ли, связанных с классическими группами над комплексными числами:

$A_{n}$ : , специальная линейная алгебра Ли . ${\mathfrak {sl}}_{n+1}$
$B_{n}$ : , нечетномерная специальная ортогональная алгебра Ли . ${\mathfrak {so}}_{2n+1}$
$C_{n}$ : , симплектическая алгебра Ли . ${\mathfrak {sp}}_{2n}$
$D_{n}$ : , четномерная специальная ортогональная алгебра Ли ( ). ${\mathfrak {so}}_{2n}$ $n>1$

Для исключительных групп названия алгебры Ли и соответствующей диаграммы Дынкина совпадают.

Связанные классификации

Диаграммы Дынкина можно интерпретировать как классификацию множества отдельных, связанных объектов, а обозначение «A _n , B _n , ...» используется для обозначения всех таких интерпретаций в зависимости от контекста; эта неоднозначность может сбивать с толку.

Основная классификация заключается в том, что простая алгебра Ли имеет корневую систему, с которой связана (ориентированная) диаграмма Дынкина; все три из них могут обозначаться , например, как B _{n .}

Неориентированная диаграмма Дынкина является формой диаграммы Коксетера и соответствует группе Вейля, которая является конечной группой отражений, связанной с корневой системой. Таким образом, B _n может относиться к неориентированной диаграмме (специальный вид диаграммы Коксетера), группе Вейля (конкретная группа отражений) или абстрактной группе Коксетера.

Хотя группа Вейля абстрактно изоморфна группе Коксетера, конкретный изоморфизм зависит от упорядоченного выбора простых корней. Аналогично, в то время как нотация диаграммы Дынкина стандартизирована, нотация диаграммы Коксетера и группы варьируется и иногда согласуется с нотацией диаграммы Дынкина, а иногда нет. ^{[ необходима цитата ]}

Наконец, иногда связанные объекты упоминаются с помощью той же нотации, хотя это не всегда можно делать регулярно. Примеры включают:

Корневая решетка, генерируемая корневой системой, как в решетке E 8 . Она определена естественным образом, но не взаимно однозначно — например, A ₂ и G ₂ оба генерируют гексагональную решетку .
Ассоциированный многогранник, например, многогранник Госсета 4 _21, может называться «многогранником E ₈ », поскольку его вершины выводятся из корневой системы E ₈ , а в качестве группы симметрии он имеет группу Коксетера E _{8 .}
Ассоциированная квадратичная форма или многообразие — например, многообразие E 8 имеет форму пересечения, заданную решеткой E ₈ .

Эти последние обозначения в основном используются для объектов, связанных с исключительными диаграммами — объекты, связанные с обычными диаграммами (A, B, C, D), вместо этого имеют традиционные имена.

Индекс ( n ) равен числу узлов в диаграмме, числу простых корней в базисе, размерности корневой решетки и охвату корневой системы, числу генераторов группы Кокстера и рангу алгебры Ли. Однако n не равен размерности определяющего модуля ( фундаментального представления ) алгебры Ли — индекс на диаграмме Дынкина не следует путать с индексом на алгебре Ли. Например, соответствует , который естественным образом действует на 9-мерном пространстве, но имеет ранг 4 как алгебра Ли. $B_{4}$ ${\mathfrak {so}}_{2\cdot 4+1}={\mathfrak {so}}_{9},$

Простые ажурные диаграммы Дынкина, не имеющие кратных ребер (A, D, E), классифицируют множество дополнительных математических объектов; см. обсуждение в классификации ADE .

Пример: А2

Например, символ может относиться к: $A_{2}$

Диаграмма Дынкина с 2 связанными узлами,, которую также можно интерпретировать как диаграмму Кокстера .
Корневая система с 2 простыми корнями, расположенными под углом (120 градусов). $2\pi /3$
Алгебра Ли ранга 2 . ${\mathfrak {sl}}_{2+1}={\mathfrak {sl}}_{3}$
Группа Вейля симметрий корней (отражения относительно гиперплоскости, ортогональной корням), изоморфная симметрической группе (порядка 6). $S_{3}$
Абстрактная группа Кокстера , представленная генераторами и отношениями, $\left\langle r_{1},r_{2}\mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1\right\rangle .$

Строительство из корневых систем

Рассмотрим корневую систему , которая предполагается приведенной и целостной (или «кристаллографической»). Во многих приложениях эта корневая система будет возникать из полупростой алгебры Ли . Пусть будет набором положительных простых корней . Затем мы построим диаграмму из следующим образом. ^[1] Сформируем граф с одной вершиной для каждого элемента . Затем вставим ребра между каждой парой вершин согласно следующему рецепту. Если корни, соответствующие двум вершинам, ортогональны, то между вершинами нет ребра. Если угол между двумя корнями составляет 120 градусов, мы помещаем одно ребро между вершинами. Если угол составляет 135 градусов, мы помещаем два ребра, а если угол составляет 150 градусов, мы помещаем три ребра. (Эти четыре случая исчерпывают все возможные углы между парами положительных простых корней. ^[2] ) Наконец, если между заданной парой вершин есть какие-либо ребра, мы украшаем их стрелкой, указывающей из вершины, соответствующей более длинному корню, в вершину, соответствующую более короткому. (Стрелка опускается, если корни имеют одинаковую длину.) Думая о стрелке как о знаке «больше чем», мы понимаем, в каком направлении должна идти стрелка. Диаграммы Дынкина приводят к классификации корневых систем. Углы и соотношения длин между корнями связаны . ^[3] Таким образом, ребра для неортогональных корней можно альтернативно описать как одно ребро для соотношения длин 1, два ребра для соотношения длин и три ребра для соотношения длин . (Когда корни ортогональны, ребер нет, независимо от соотношения длин.) $\Delta$ $\Delta$ $\Delta$ ${\sqrt {2}}$ ${\sqrt {3}}$

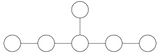
В корневой системе, показанной справа, корни, обозначенные и, образуют основание. Поскольку эти два корня находятся под углом 120 градусов (с отношением длин 1), диаграмма Дынкина состоит из двух вершин, соединенных одним ребром: $A_{2}$ $\alpha$ $\beta$ .

Ограничения

Диаграммы Дынкина должны удовлетворять определенным ограничениям; по сути, это те, которым удовлетворяют конечные диаграммы Кокстера–Дынкина , вместе с дополнительным кристаллографическим ограничением.

Связь с диаграммами Коксетера

Диаграммы Дынкина тесно связаны с диаграммами Коксетера конечных групп Коксетера , и терминология часто смешивается. ^{[примечание 1]}

Диаграммы Дынкина отличаются от диаграмм Кокстера конечных групп в двух важных отношениях:

Частично направленный: Диаграммы Дынкина частично направлены — любое кратное ребро (в терминах Коксетера, обозначенное цифрой «4» или выше) имеет направление (стрелку, указывающую от одного узла к другому); таким образом, диаграммы Дынкина содержат больше данных, чем базовая диаграмма Коксетера (неориентированный граф).; На уровне корневых систем направление соответствует направлению к более короткому вектору; ребра, помеченные «3», не имеют направления, поскольку соответствующие векторы должны иметь одинаковую длину. (Внимание: некоторые авторы меняют это соглашение на противоположное, и стрелка указывает к более длинному вектору.)
Кристаллографическое ограничение: Диаграммы Дынкина должны удовлетворять дополнительному ограничению, а именно, что единственными допустимыми метками ребер являются 2, 3, 4 и 6, ограничение, которого нет у диаграмм Коксетера, поэтому не каждая диаграмма Коксетера конечной группы происходит от диаграммы Дынкина.; На уровне корневых систем это соответствует теореме о кристаллографическом ограничении , поскольку корни образуют решетку.

Еще одно отличие, которое носит исключительно стилистический характер, заключается в том, что диаграммы Дынкина традиционно рисуются с двойными или тройными ребрами между узлами (для p = 4, 6), а не с ребром, помеченным как « p ».

Термин «диаграмма Дынкина» иногда относится к направленному графу, иногда к ненаправленному графу. Для точности в этой статье «диаграмма Дынкина» будет означать направленный, а лежащий в основе ненаправленный граф будет называться «ненаправленной диаграммой Дынкина». Тогда диаграммы Дынкина и диаграммы Коксетера могут быть связаны следующим образом:

Под этим подразумевается, что диаграммы Кокстера конечных групп соответствуют точечным группам, порожденным отражениями, в то время как диаграммы Дынкина должны удовлетворять дополнительному ограничению, соответствующему теореме о кристаллографическом ограничении , и что диаграммы Кокстера являются ненаправленными, в то время как диаграммы Дынкина (частично) направленными.

Соответствующие математические объекты, классифицированные по диаграммам:

Пробел в правом верхнем углу, соответствующий ориентированным графам с неориентированным графом в основе любой диаграммы Коксетера (конечной группы), может быть определен формально, но он мало обсуждается и, по-видимому, не допускает простой интерпретации в терминах интересующих нас математических объектов.

Существуют естественные отображения вниз — от диаграмм Дынкина к неориентированным диаграммам Дынкина; соответственно, от корневых систем к связанным группам Вейля — и вправо — от неориентированных диаграмм Дынкина к диаграммам Кокстера; соответственно, от групп Вейля к конечным группам Кокстера.

Отображение вниз является отображением на (по определению), но не взаимно-однозначным, поскольку диаграммы B _n и C _n отображаются в одну и ту же неориентированную диаграмму, при этом результирующая диаграмма Кокстера и группа Вейля поэтому иногда обозначаются как BC _n .

Правое отображение является просто включением — неориентированные диаграммы Дынкина являются частными случаями диаграмм Коксетера, а группы Вейля являются частными случаями конечных групп Коксетера — и не является включением, поскольку не каждая диаграмма Коксетера является неориентированной диаграммой Дынкина (пропущенными диаграммами являются H ₃ , H ₄ и I ₂ ( p ) для p = 5 p ≥ 7), и, соответственно, не каждая конечная группа Коксетера является группой Вейля.

Изоморфизмы

Диаграммы Дынкина условно нумеруются так, чтобы список не был избыточным: для для для для для и начиная с Семейства, однако, могут быть определены для меньших n, что даёт исключительные изоморфизмы диаграмм и соответствующие исключительные изоморфизмы алгебр Ли и связанных групп Ли. $n\geq 1$ $A_{n},$ $n\geq 2$ $B_{n},$ $n\geq 3$ $C_{n},$ $n\geq 4$ $D_{n},$ $E_{n}$ $n=6.$

Тривиально, можно начать семейства с или , которые затем все изоморфны, поскольку есть уникальная пустая диаграмма и уникальная 1-узловая диаграмма. Другие изоморфизмы связных диаграмм Дынкина: $n=0$ $n=1,$

$A_{1}\cong B_{1}\cong C_{1}$
$B_{2}\cong C_{2}$
$D_{2}\cong A_{1}\times A_{1}$
$D_{3}\cong A_{3}$
$E_{3}\cong A_{1}\times A_{2}$
$E_{4}\cong A_{4}$
$E_{5}\cong D_{5}$

Эти изоморфизмы соответствуют изоморфизму простых и полупростых алгебр Ли, которые также соответствуют определенным изоморфизмам групповых форм Ли этих алгебр. Они также добавляют контекст к семейству E n . ^[4]

Автоморфизмы

Наиболее симметричной диаграммой Дынкина является D4 _, что приводит к триальности .

В дополнение к изоморфизму между различными диаграммами, некоторые диаграммы также имеют самоизоморфизмы или « автоморфизмы ». Автоморфизмы диаграмм соответствуют внешним автоморфизмам алгебры Ли, что означает, что группа внешних автоморфизмов Out = Aut/Inn равна группе автоморфизмов диаграмм. ^[5]^[6]^[7]

Диаграммы, имеющие нетривиальные автоморфизмы, — это A _n ( ), D _n ( ) и E ₆ . Во всех этих случаях, за исключением D ₄ , имеется один нетривиальный автоморфизм (Out = C ₂ , циклическая группа порядка 2), тогда как для D ₄ группа автоморфизмов — это симметрическая группа по трем буквам ( S ₃ , порядок 6) — это явление известно как « троичность ». Бывает, что все эти автоморфизмы диаграмм могут быть реализованы как евклидовы симметрии того, как диаграммы традиционно рисуются на плоскости, но это всего лишь артефакт того, как они рисуются, а не внутренняя структура. $n>1$ $n>1$

А _н .

Для A _n автоморфизм диаграммы обращает диаграмму, которая является линией. Узлы диаграммы индексируют фундаментальные веса , которые (для A _{n −1} ) равны для , а автоморфизм диаграммы соответствует дуальности Реализованный как алгебра Ли, внешний автоморфизм может быть выражен как отрицательное транспонирование, , что является тем, как действует дуальное представление. ^[6] $\bigwedge ^{i}C^{n}$ $i=1,\dots ,n$ $\bigwedge ^{i}C^{n}\mapsto \bigwedge ^{n-i}C^{n}.$ ${\mathfrak {sl}}_{n+1},$ $T\mapsto -T^{\mathrm {T} }$

Для D _n автоморфизм диаграммы переключает два узла в конце Y и соответствует переключению двух хиральных спиновых представлений . Реализованный как алгебра Ли внешний автоморфизм может быть выражен как сопряжение матрицей в O(2 n ) с определителем −1. Когда n = 3, то их автоморфизмы совпадают, в то время как является несвязным, и автоморфизм соответствует переключению двух узлов. ${\mathfrak {so}}_{2n},$ $\mathrm {D} _{3}\cong \mathrm {A} _{3},$ $\mathrm {D} _{2}\cong \mathrm {A} _{1}\times \mathrm {A} _{1}$

Для D ₄ фундаментальное представление изоморфно двум спиновым представлениям, и результирующая симметрическая группа с тремя буквами ( S ₃ , или, альтернативно, диэдральная группа порядка 6, Dih ₃ ) соответствует как автоморфизмам алгебры Ли, так и автоморфизмам диаграммы.

Э ₆ .

Группа автоморфизмов E ₆ соответствует обращению диаграммы и может быть выражена с помощью йордановых алгебр . ^[6]^[8]

Несвязные диаграммы, соответствующие полупростым алгебрам Ли, могут иметь автоморфизмы, возникающие при перестановке компонентов диаграммы.

В характеристике 2 стрелку на F ₄ можно игнорировать, что даёт дополнительный автоморфизм диаграммы и соответствующие группы Сузуки–Ри .

В положительной характеристике есть дополнительные «диаграммные автоморфизмы» — грубо говоря, в характеристике p иногда разрешается игнорировать стрелку на связях кратности p в диаграмме Дынкина при рассмотрении диаграммных автоморфизмов. Таким образом, в характеристике 2 есть автоморфизм порядка 2 для и для F ₄ , тогда как в характеристике 3 есть автоморфизм порядка 2 для G ₂ . Но не применяется во всех обстоятельствах: например, такие автоморфизмы не обязательно должны возникать как автоморфизмы соответствующей алгебраической группы, а скорее на уровне точек, имеющих значения в конечном поле. $\mathrm {B} _{2}\cong \mathrm {C} _{2}$

Построение групп Ли с помощью диаграммных автоморфизмов

Автоморфизмы диаграмм, в свою очередь, дают дополнительные группы Ли и группы типа Ли , которые имеют центральное значение в классификации конечных простых групп.

Конструкция группы Шевалле групп Ли в терминах их диаграммы Дынкина не дает некоторых классических групп, а именно унитарных групп и нерасщепленных ортогональных групп . Группы Стейнберга строят унитарные группы ² A _n , в то время как другие ортогональные группы строятся как ² D _n , где в обоих случаях это относится к объединению автоморфизма диаграммы с автоморфизмом поля. Это также дает дополнительные экзотические группы Ли ² E ₆ и ³ D ₄ , последняя определена только над полями с автоморфизмом порядка 3.

Дополнительные автоморфизмы диаграмм в положительной характеристике дают группы Сузуки–Ри , ² B ₂ , ² F ₄ и ² G ₂ .

Складной

Конечные групповые складывания Коксетера.

Аффинные групповые свертывания Коксетера с тремя соглашениями об именовании: первое — исходное расширенное множество; второе — используемое в контексте колчанных графов; и последнее — Виктора Каца для скрученных аффинных алгебр Ли .

(Просто-шнурованная) диаграмма Дынкина (конечная или аффинная ), имеющая симметрию (удовлетворяющую одному условию, ниже), может быть факторизована по симметрии, давая новую, в общем случае многократно-шнурованную диаграмму, с процессом, называемым сворачиванием (из-за того, что большинство симметрий являются 2-кратными). На уровне алгебр Ли это соответствует взятию инвариантной подалгебры под внешнюю группу автоморфизмов, и процесс может быть определен исключительно со ссылкой на корневые системы, без использования диаграмм. ^[9] Кроме того, каждая многократно-шнурованная диаграмма (конечная или бесконечная) может быть получена путем сворачивания просто-шнурованной диаграммы. ^[10]

Единственное условие автоморфизма для возможности сворачивания состоит в том, что различные узлы графа в одной и той же орбите (при автоморфизме) не должны быть соединены ребром; на уровне корневых систем корни в одной и той же орбите должны быть ортогональны. ^[10] На уровне диаграмм это необходимо, так как в противном случае фактор-диаграмма будет иметь петлю из-за идентификации двух узлов, но наличия ребра между ними, а петли не допускаются в диаграммах Дынкина.

Узлы и ребра факторной («свернутой») диаграммы являются орбитами узлов и ребер исходной диаграммы; ребра являются одинарными, если только два инцидентных ребра не отображаются на одно и то же ребро (особенно в узлах с валентностью больше 2) – «точка ветвления» карты, в этом случае вес равен числу инцидентных ребер, а стрелка указывает на узел, в котором они инцидентны – «точка ветвления отображается на неоднородную точку». Например, в D _{4 ,} сворачивающемся в G ₂ , ребро в G ₂ указывает из класса 3 внешних узлов (валентность 1) в класс центрального узла (валентность 3).

Складывания конечных диаграмм следующие: ^[11]^{[примечание 2]}

$A_{2n-1}\to C_{n}$

(Автоморфизм A _{2 n} не приводит к складыванию, поскольку два средних узла соединены ребром, но находятся на одной орбите.)

$D_{n+1}\to B_{n}$
$D_{4}\to G_{2}$ (если факторизуем по полной группе или 3-циклу, в дополнение к 3 различным способам, если факторизуем по инволюции) $D_{4}\to B_{3}$
$E_{6}\to F_{4}$

Аналогичные свертывания существуют для аффинных диаграмм, включая:

${\tilde {A}}_{2n-1}\to {\tilde {C}}_{n}$
${\tilde {D}}_{n+1}\to {\tilde {B}}_{n}$
${\tilde {D}}_{4}\to {\tilde {G}}_{2}$
${\tilde {E}}_{6}\to {\tilde {F}}_{4}$

Понятие складок может быть также применено в более общем смысле к диаграммам Коксетера ^[12] – в частности, можно обобщить допустимые факторы диаграмм Дынкина до H _n и I ₂ ( p ). Геометрически это соответствует проекциям однородных многогранников . В частности, любую просто зашнурованную диаграмму Дынкина можно сложить до I ₂ ( h ), где h – число Коксетера , что геометрически соответствует проекции на плоскость Коксетера .

Сворачивание можно применять для сведения вопросов о (полупростых) алгебрах Ли к вопросам о просто-шнурованных алгебрах вместе с автоморфизмом, что может быть проще, чем напрямую рассматривать многошнурованные алгебры; это можно сделать, например, при построении полупростых алгебр Ли. См. Math Overflow: Folding by Automorphisms для дальнейшего обсуждения.

Другие карты диаграмм

Некоторые дополнительные карты диаграмм имеют содержательные интерпретации, как подробно описано ниже. Однако не все карты корневых систем возникают как карты диаграмм. ^[13]

Например, есть два включения корневых систем A ₂ в G ₂ , либо как шесть длинных корней, либо как шесть коротких корней. Однако узлы на диаграмме G ₂ соответствуют одному длинному корню и одному короткому корню, тогда как узлы на диаграмме A ₂ соответствуют корням одинаковой длины, и, таким образом, эта карта корневых систем не может быть выражена как карта диаграмм.

Некоторые включения корневых систем можно выразить как одну диаграмму, являющуюся индуцированным подграфом другой, что означает «подмножество узлов со всеми ребрами между ними». Это происходит потому, что удаление узла из диаграммы Дынкина соответствует удалению простого корня из корневой системы, что дает корневую систему ранга на единицу ниже. Напротив, удаление ребра (или изменение кратности ребра) при сохранении узлов неизменными соответствует изменению углов между корнями, что невозможно сделать без изменения всей корневой системы. Таким образом, можно осмысленно удалить узлы, но не ребра. Удаление узла из связной диаграммы может дать связную диаграмму (простую алгебру Ли), если узел является листом, или несвязную диаграмму (полупростую, но не простую алгебру Ли) с двумя или тремя компонентами (последнее для D _n и E _n ). На уровне алгебр Ли эти включения соответствуют подалгебрам Ли.

Максимальные подграфы следующие; подграфы, связанные автоморфизмом диаграммы, называются «сопряженными»:

A _{n +1} : A _n , двумя сопряженными способами.
Bn ₊₁ : _An , _Bn .
C _{n +1} : A _n , C _n .
D _{n +1} : A _n (2 сопряженных способа), D _n .
Эн ₊₁ : _Эн , _Дн , _Эн .
- Для E ₆ два из них совпадают: и сопряжены. $\mathrm {D} _{5}\cong \mathrm {E} _{5}$
Ф ₄ : В ₃ , С ₃ .
G ₂ : A ₁ , двумя несопряженными способами (как длинный корень или как короткий корень).

Наконец, двойственность диаграмм соответствует изменению направления стрелок, если таковые имеются: ^[13] B _n и C _n являются двойственными, тогда как F ₄ и G ₂ являются самодвойственными, как и просто зашнурованные диаграммы ADE.

Просто зашнурованный

Диаграмма Дынкина без кратных ребер называется просто кружевной , как и соответствующая алгебра Ли и группа Ли. Это диаграммы , и явления, которые такие диаграммы классифицируют, называются классификацией ADE . В этом случае диаграммы Дынкина в точности совпадают с диаграммами Коксетера, поскольку нет кратных ребер. $A_{n},D_{n},E_{n}$

Диаграммы Сатаке

Диаграммы Дынкина классифицируют комплексные полупростые алгебры Ли. Действительные полупростые алгебры Ли можно классифицировать как действительные формы комплексных полупростых алгебр Ли, и они классифицируются диаграммами Сатаке , которые получаются из диаграммы Дынкина путем маркировки некоторых вершин черным цветом (заполненными) и соединения некоторых других вершин попарно стрелками в соответствии с определенными правилами.

История

Диаграммы Дынкина названы в честь Евгения Дынкина , который использовал их в двух работах (1946, 1947), упрощающих классификацию полупростых алгебр Ли; ^[14] см. (Дынкин 2000). Когда Дынкин покинул Советский Союз в 1976 году, что в то время считалось равносильным измене, советским математикам было предписано ссылаться на «диаграммы простых корней», а не использовать его имя. ^{[ необходима цитата ]}

Неориентированные графы использовались ранее Кокстером (1934) для классификации групп отражений , где узлы соответствовали простым отражениям; затем эти графы (с информацией о длине) использовал Витт (1941) применительно к корневым системам, причем узлы соответствовали простым корням, как они используются сегодня. ^[14]^[15] Затем Дынкин использовал их в 1946 и 1947 годах, отдав должное Кокстеру и Витту в своей статье 1947 года.

Конвенции

Диаграммы Дынкина были нарисованы несколькими способами; ^[15] соглашение, которому следуют здесь, является общим, с углами 180° на узлах валентности 2, углами 120° на узле валентности 3 D _n и углами 90°/90°/180° на узле валентности 3 E _n , с кратностью, обозначенной 1, 2 или 3 параллельными ребрами, и длиной корня, обозначенной стрелкой на ребре для ориентации. Помимо простоты, еще одним преимуществом этого соглашения является то, что автоморфизмы диаграмм реализуются посредством евклидовых изометрий диаграмм.

Альтернативные соглашения включают написание числа у края для указания кратности (обычно используется в диаграммах Коксетера), затемнение узлов для указания длины корня или использование углов 120° на узлах валентности 2, чтобы сделать узлы более различимыми.

Существуют также соглашения о нумерации узлов. Наиболее распространенное современное соглашение было разработано к 1960-м годам и проиллюстрировано в (Bourbaki 1968). ^[15]

Диаграммы Дынкина ранга 2

Диаграммы Дынкина эквивалентны обобщенным матрицам Картана , как показано в этой таблице диаграмм Дынкина ранга 2 с соответствующими им матрицами Картана $2 \times 2$ .

Для ранга 2 форма матрицы Картана имеет вид:

A=\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]

Многореберная диаграмма соответствует недиагональным элементам матрицы Картана ⁠ ⁠ $-a_{21},-a_{12}$ , с числом нарисованных ребер, равным ⁠ ⁠ $\max(-a_{21},-a_{12})$ , и стрелкой, указывающей на элементы, отличные от единицы.

Обобщенная матрица Картана — это квадратная матрица, такая что: $A=(a_{ij})$

Для диагональных записей, . $a_{ii}=2$
Для недиагональных записей, . $a_{ij}\leq 0$
$a_{ij}=0$ если и только если $a_{ji}=0$

Матрица Картана определяет, является ли группа конечного типа (если это положительно определенная матрица , т. е. все собственные значения положительны), аффинного типа (если это не положительно определенная, а положительно полуопределенная, т. е. все собственные значения неотрицательны) или неопределенного типа . Неопределенный тип часто далее подразделяется, например, группа Коксетера является лоренцевой, если она имеет одно отрицательное собственное значение, а все остальные собственные значения положительны. Более того, несколько источников ссылаются на гиперболические группы Коксетера, но существует несколько неэквивалентных определений для этого термина. В обсуждении ниже гиперболические группы Коксетера являются частным случаем лоренцевых, удовлетворяющим дополнительному условию. Для ранга 2 все отрицательно детерминантные матрицы Картана соответствуют гиперболической группе Коксетера. Однако в целом большинство матриц с отрицательным детерминантом не являются ни гиперболическими, ни лоренцевыми.

Конечные ветви имеют , а аффинные ветви (с нулевым определителем) имеют ⁠ ⁠ . $(-a_{21},-a_{12})=(1,1),(2,1),(3,1)$ $(-a_{21},-a_{12})=(2,2){\text{ or }}(4,1)$

Конечные диаграммы Дынкина

Аффинные диаграммы Дынкина

Существуют расширения диаграмм Дынкина, а именно аффинные диаграммы Дынкина ; они классифицируют матрицы Картана аффинных алгебр Ли . Они классифицированы в (Kac 1994, Глава 4, стр. 47–), в частности, перечислены в (Kac 1994, стр. 53–55). Аффинные диаграммы обозначаются как или , где X — буква соответствующей конечной диаграммы, а показатель степени зависит от того, в какой серии аффинных диаграмм они находятся. Первые из них наиболее распространены и называются расширенными диаграммами Дынкина и обозначаются тильдой , а также иногда помечаются верхним индексом + . ^[17] как в . Серии (2) и (3) называются скрученными аффинными диаграммами . $X_{l}^{(1)},X_{l}^{(2)},$ $X_{l}^{(3)},$ $X_{l}^{(1)},$ ${\tilde {A}}_{5}=A_{5}^{(1)}=A_{5}^{+}$

Для получения диаграмм см. Генератор диаграмм Дынкина.

Вот все графы Дынкина для аффинных групп до 10 узлов. Расширенные графы Дынкина даны как ~ семейства, такие же, как конечные графы выше, с одним добавленным узлом. Другие вариации направленных графов даны с верхним индексом (2) или (3), представляющим сворачивания групп более высокого порядка. Они классифицируются как скрученные аффинные диаграммы. ^[18]

Гиперболические и высшие диаграммы Дынкина

Перечислено множество компактных и некомпактных гиперболических графов Дынкина. ^[19] Все гиперболические графы ранга 3 являются компактными. Компактные гиперболические диаграммы Дынкина существуют до ранга 5, а некомпактные гиперболические графы существуют до ранга 10.

Компактные гиперболические диаграммы Дынкина

Некомпактные (сверхрасширенные) формы

Некоторые обозначения, используемые в теоретической физике , такие как М-теория , используют верхний индекс «+» для расширенных групп вместо «~», что позволяет определять группы более высоких расширений.

Расширенные диаграммы Дынкина (аффинные) обозначены знаком «+» и представляют собой один добавленный узел. (То же, что и «~»).
Расширенные диаграммы Дынкина (гиперболические) обозначаются символами «^» или «++» и представляют собой два дополнительных узла.
Очень расширенные диаграммы Дынкина с тремя добавленными узлами обозначены «+++».

238 Гиперболические группы (компактные и некомпактные)

238 гиперболических групп (компактных и некомпактных) ранга названы и перечислены для каждого ранга. $n\geq 3$ $H_{i}^{(n)}$ $i=1,2,3...$

Очень-расширенный

Очень расширенные группы — это группы Лоренца , определяемые добавлением трех узлов к конечным группам. E ₈ , E ₇ , E ₆ , F ₄ и G ₂ предлагают шесть серий, заканчивающихся как очень расширенные группы. Другие расширенные серии, не показанные, могут быть определены из A _n , B _n , C _n и D _n , как различные серии для каждого n . Определитель связанной матрицы Картана определяет, где серия изменяется от конечной (положительной) до аффинной (нулевой) к некомпактной гиперболической группе (отрицательной) и заканчивается как группа Лоренца, которая может быть определена с использованием одного времениподобного измерения и используется в теории М . ^[20]

Смотрите также

На Викискладе есть медиафайлы по теме «Диаграммы Дынкина» .

Диаграмма Сатаке
Список неприводимых индексов Титса
Klassifikation von Wurzelsystemen (Классификация корневых систем) (на немецком языке)

Примечания

^ В этом разделе мы называем общий класс «диаграммами Коксетера», а не «диаграммами Коксетера–Дынкина» для ясности, поскольку существует большая вероятность путаницы, а также для краткости.
^ Обратите внимание, что «Стеклощик» использует условные обозначения стрелок, противоположные принятым в данной статье.

Цитаты

^ Холл 2015 Раздел 8.6
^ Холл 2015 Предложения 8.6 и 8.13
^ Холл 2015 Предложение 8.6
↑ Баез, Джон (13 апреля 1998 г.), Находки этой недели в математической физике (неделя 119)
^ Фултон и Харрис 1991, Предложение D.40
^ abc Внешние автоморфизмы простых алгебр Ли
^ Хамфрис 1972, § 16.5
^ Якобсон 1971, § 7
^ Алгебраическая геометрия и теория чисел: в честь 50-летия Владимира Дринфельда, под редакцией Виктора Гинзбурга, стр. 47, раздел 3.6: Кластерное сворачивание
^ ab Сворачивание с помощью автоморфизмов Архивировано 2016-03-04 в Wayback Machine , Джон Стембридж, 4 стр., 79K, 20 августа 2008 г., Другие статьи Джона Стембриджа
^ См. Стекольщик 2008, стр. 102, примечание 5.4 для иллюстраций этих складок и ссылок.
^ Зубер, Жан-Бернард (1998). «Обобщенные диаграммы Дынкина и корневые системы и их складывание». В Kashiwara, M.; Matsuo, A.; Saito, K.; Satake, I. (ред.). Топологическая теория поля, примитивные формы и смежные темы . Progress in Mathematics. Vol. 160. pp. 28–30. CiteSeerX 10.1.1.54.3122 . doi :10.1007/978-1-4612-0705-4_16. ISBN 978-1-4612-6874-1. S2CID 12429369.
^ ab Армстронг, Джон (5 марта 2010 г.). «Преобразования диаграмм Дынкина».
^ ab Knapp 2002, стр. 758
^ abc Почему диаграммы Дынкина E6, E7 и E8 всегда рисуются именно так, как они рисуются?
↑ Раздел 2.1 в книге Стекольщик, Рафаэль (2005). «Заметки о преобразованиях Кокстера и соответствии Маккея». arXiv : math/0510216v1 .
^ См., например, Хамфрис, Джеймс Э. (1990). "48. Фундаментальная область § Аффинные группы отражения". Группы отражения и группы Коксетера . Cambridge University Press. стр. 96. ISBN 978-0-521-43613-7.
^ Кац, Виктор Г. (1990). "4. Классификация обобщенных матриц Картана". Бесконечномерные алгебры Ли . Cambridge University Press. стр. 53–. ISBN 978-0-521-46693-6.
^ Карбоне, Лиза; Чунг, Сьювон; Коббс, Ли; Макрей, Роберт; Нанди, Дебайоти; Накви, Юсра; Пента, Диего (2010). «Классификация гиперболических диаграмм Дынкина, длин корней и орбит группы Вейля». Журнал физики A: Математическое и теоретическое . 43 (15): 155209. arXiv : 1003.0564 . Bibcode :2010JPhA...43o5209C. doi :10.1088/1751-8113/43/15/155209. S2CID 16946456.
^ Энглерт, Франсуа; Уарт, Лоран; Таормина, Энн ; Уэст, Питер (2003). «Симметрия М-теорий». Журнал физики высоких энергий . 2003 (9): 020. arXiv : hep-th/0304206 . Bibcode : 2003JHEP...09..020E. doi : 10.1088/1126-6708/2003/09/020. S2CID 15680493.

Ссылки

Дынкин, Е.Б. (1947), «Строение полупростых алгебр», Успехи математических наук , НС, 2 (4(20)): 59–127
Бурбаки, Николя (1968), «Главы 4–6», Groupes et algebres de Lie , Париж: Герман
Якобсон, Натан (1971-06-01), Исключительные алгебры Ли , CRC Press, ISBN 978-0-8247-1326-3
Хамфрис, Джеймс Э. (1972), Введение в алгебры Ли и теорию представлений , Биркхойзер, ISBN 978-0-387-90053-7
Фултон, Уильям ; Харрис, Джо (1991). Теория представлений. Первый курс . Graduate Texts in Mathematics , Readings in Mathematics. Том 129. Нью-Йорк: Springer-Verlag. doi :10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.
Дынкин, Евгений Борисович; Александр Адольф Юшкевич; Гэри М. Зейтц; А. Л. Онищик (2000), Избранные статьи Э. Б. Дынкина с комментариями , AMS Bookstore, ISBN 978-0-8218-1065-1
Холл, Брайан С. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Graduate Texts in Mathematics, т. 222 (2-е изд.), Springer, ISBN 978-3319134666
Кнапп, Энтони В. (2002), Группы Ли после введения (2-е изд.), Биркхойзер, ISBN 978-0-8176-4259-4
Стекольщик, Р. (2008), Заметки о преобразованиях Кокстера и переписке Маккея , Springer Monographs in Mathematics, arXiv : math/0510216 , doi :10.1007/978-3-540-77399-3, ISBN 978-3-540-77398-6, S2CID 117958873
Карбоне, Лиза; Чунг, Сьювон; Коббс, Ли; Макрэ, Роберт; Нанди, Дебайоти; Навки, Юсра; Пента, Диего (март 2010 г.), «Классификация гиперболических диаграмм Дынкина, длины корней и орбиты группы Вейля». (PDF) , Журнал физики A: Математические и теоретические , 43 (15): 155209, arXiv : 1003.0564 , Bibcode :2010JPhA...43o5209C, doi :10.1088/1751-8113/43/15/155209, MR 2608277, S2CID 16946456
Кац, Виктор Г. (1994). Бесконечномерные алгебры Ли. Cambridge University Press. ISBN 978-0-521-46693-6.
Дынкин, Евгений Б. (2000). Юшкевич, А.А.; Зейтц , Г.М.; Онищик, А.Л. (ред.). Избранные статьи Э.Б. Дынкина с комментариями. Провиденс, Род-Айленд: Американское математическое общество. ISBN 978-0-8218-1065-1. МР 1757976.

Внешние ссылки

Джон Баэз о повсеместном использовании диаграмм Дынкина в математике
Веб-инструмент для создания диаграмм Динкина с метками, пригодных для публикации (написан на JavaScript)