Распределительная решетка

В математике дистрибутивная решетка — это решетка , в которой операции соединения и встречи распределяются друг по другу. Прототипическими примерами таких структур являются коллекции множеств, для которых операции над решеткой могут быть заданы объединением и пересечением множеств . Действительно, эти решетки множеств полностью описывают декорации: каждая дистрибутивная решетка — с точностью до изоморфизма — задана как таковая решетка множеств.

Определение

Как и в случае с произвольными решетками, дистрибутивную решетку L можно рассматривать либо как структуру теории порядка , либо как структуру универсальной алгебры . Оба взгляда и их взаимное соответствие обсуждаются в статье о решетках . В данной ситуации алгебраическое описание представляется более удобным.

Решетка ( L , ∨, ∧) является дистрибутивной , если для всех x , y и z в L выполняется следующее дополнительное тождество :

Икс ∧ ( y ∨ z ) знак равно ( Икс ∧ y ) ∨ ( Икс ∧ z ).

Рассматривая решетки как частично упорядоченные множества, это говорит о том, что операция встречи сохраняет непустые конечные соединения. Основной факт теории решеток состоит в том, что приведенное выше условие эквивалентно двойственному ему : ^[1]

Икс ∨ ( y ∧ z ) знак равно ( Икс ∨ y ) ∧ ( Икс ∨ z ) для всех x , y и z в L .

Если в каждой решетке отношение порядка p ≤ q определяется, как обычно, как p ∧ q = p , то неравенство x ∧ ( y ∨ z ) ≥ ( x ∧ y ) ∨ ( x ∧ z ) и двойственное ему x ∨ ( y ∧ z ) ≤ ( x ∨ y ) ∧ ( x ∨ z ) всегда верны. Решетка называется дистрибутивной, если выполнено хотя бы одно из обратных неравенств. Более подробную информацию о связи этого условия с другими условиями дистрибутивности теории порядка можно найти в статье Дистрибутивность (теория порядка) .

Морфизмы

Морфизм дистрибутивных решеток — это просто гомоморфизм решетки, как указано в статье о решетках , то есть функция, совместимая с двумя решеточными операциями. Поскольку такой морфизм решеток сохраняет структуру решетки, он, следовательно, сохранит и дистрибутивность (и, таким образом, будет морфизмом дистрибутивных решеток).

Примеры

Решетка Юнга

Дистрибутивные решетки являются повсеместными, но также и довольно специфическими структурами. Как уже упоминалось, основным примером дистрибутивных решеток являются решетки множеств, где соединение и соединение задаются обычными теоретико-множественными операциями. Дополнительные примеры включают в себя:

• Алгебра Линденбаума большинства логик , поддерживающих конъюнкцию и дизъюнкцию, представляет собой дистрибутивную решетку, т. е. «и» распределяется над «или» и наоборот.
• Любая булева алгебра является дистрибутивной решеткой.
• Любая гейтинговая алгебра является дистрибутивной решеткой. Особенно это касается всех локалей и, следовательно, всех открытых множеств топологических пространств . Также отметим, что алгебры Гейтинга можно рассматривать как алгебры Линденбаума интуиционистской логики , что делает их частным случаем первого примера.
• Каждое полностью упорядоченное множество представляет собой дистрибутивную решетку с max в качестве соединения и min в качестве соединения.
• Натуральные числа образуют (условно полную) дистрибутивную решетку, принимая наибольший общий делитель за встречу и наименьшее общее кратное за соединение. Эта решетка также имеет наименьший элемент, а именно 1, который, следовательно, служит единичным элементом для соединений.
• Учитывая положительное целое число n , набор всех положительных делителей n образует дистрибутивную решетку, снова с наибольшим общим делителем в качестве встречи и наименьшим общим кратным в качестве соединения. Это булева алгебра тогда и только тогда, когда n свободно от квадратов .
• Решетчато -упорядоченное векторное пространство является дистрибутивной решеткой.
• Решетка Юнга , заданная упорядочением включения диаграмм Юнга , представляющих целочисленные разбиения, является дистрибутивной решеткой.
• Точки дистрибутивного многогранника ( выпуклый многогранник, замкнутый относительно операций покоординатного минимума и покоординатного максимума), где эти две операции являются операциями соединения и встречи решетки. ^[2]

В начале разработки теории решеток Чарльз С. Пирс считал, что все решетки дистрибутивны, то есть дистрибутивность следует из остальных аксиом решетки. ^{[3] [4]} Однако доказательства независимости были даны Шредером , Фойгтом, ^(де) Люротом , Корсельтом , ^[5] и Дедекиндом . ^[3]

Характерные свойства

Диаграммы Хассе двух прототипов недистрибутивных решеток. Алмазная решетка M ₃ недистрибутивна, поскольку x ∧ ( y ∨ z ) = x ∧ 1 = x ≠ 0 = 0 ∨ 0 = ( x ∧ y ) ∨ ( x ∧ z ) , а пятиугольная решетка N ₅ не является -дистрибутивен, потому что Икс ∧ ( y ∨ z ) знак равно Икс ∧ 1 знак равно Икс ≠ z знак равно 0 ∨ z знак равно ( Икс ∧ y ) ∨ ( Икс ∧ z )

Существуют различные эквивалентные формулировки приведенному выше определению. Например, L является дистрибутивным тогда и только тогда, когда для всех элементов x , y , z в L выполняется следующее :

$${\displaystyle (x\wedge y)\vee (y\wedge z)\vee (z\wedge x)=(x\vee y)\wedge (y\vee z)\wedge (z\vee x).}$$

L

${\displaystyle x\wedge z=y\wedge z}$и всегда подразумеваю ${\displaystyle x\vee z=y\vee z}$ ${\displaystyle x=y.}$

Дистрибутивная решетка, которая содержит N5 (сплошные линии слева) и M3 (справа) в качестве подмножества , но не в качестве подрешетки .

Простейшими нераспределительными решетками являются M ₃ , «ромбовидная решетка», и N ₅ , «пятиугольная решетка». Решетка дистрибутивна тогда и только тогда, когда ни одна из ее подрешеток не изоморфна M ₃ или  N ₅ ; Подрешетка — это подмножество, замкнутое относительно операций соединения и соединения исходной решетки. Обратите внимание, что это не то же самое, что подмножество, представляющее собой решетку в исходном порядке (но, возможно, с другими операциями соединения и соединения). Дальнейшие характеристики вытекают из теории представлений в следующем разделе.

Альтернативный способ констатировать тот же факт состоит в том, что каждая дистрибутивная решетка является подпрямым произведением копий двухэлементной цепи или что единственным подпрямо неприводимым членом класса дистрибутивных решеток является двухэлементная цепь. Как следствие, каждая булева решетка также обладает этим свойством. ^[6]

Наконец, дистрибутивность влечет за собой несколько других приятных свойств. Например, элемент дистрибутивной решетки является встречно-простым тогда и только тогда, когда он является встречно-неприводимым , хотя последнее, как правило, является более слабым свойством. В силу двойственности то же самое верно для простых и неприводимых элементов. ^[7] Если решетка дистрибутивна, ее накрывающее отношение образует медианный граф . ^[8]

Более того, каждая дистрибутивная решетка также является модулярной .

Теория представлений

Введение уже намекало на наиболее важную характеристику дистрибутивных решеток: решетка дистрибутивна тогда и только тогда, когда она изоморфна решетке множеств (замкнутой относительно объединения и пересечения множеств ). (Последнюю структуру в этом контексте иногда называют кольцом множеств .) То, что объединение и пересечение множеств действительно являются дистрибутивными в указанном выше смысле, является элементарным фактом. Другое направление менее тривиально, поскольку требует сформулированных ниже теорем о представлении . Важным выводом из этой характеристики является то, что тождества (уравнения), которые выполняются во всех дистрибутивных решетках, являются именно теми, которые выполняются во всех решетках множеств в указанном выше смысле.

Теорема Биркгофа о представлении дистрибутивных решеток утверждает, что каждая конечная дистрибутивная решетка изоморфна решетке нижних множеств ЧУУ ее простых по соединению (что эквивалентно: неприводимых по объединению) элементов. Это устанавливает биекцию (с точностью до изоморфизма ) между классом всех конечных частично упорядоченных множеств и классом всех конечных дистрибутивных решеток. Эту биекцию можно расширить до двойственности категорий между гомоморфизмами конечных дистрибутивных решеток и монотонными функциями конечных частично упорядоченных множеств. Однако обобщение этого результата на бесконечные решетки требует добавления дополнительной структуры.

Другая ранняя теорема о представлении теперь известна как теорема Стоуна о представлении дистрибутивных решеток (название в честь Маршалла Харви Стоуна , который первым ее доказал). Он характеризует дистрибутивные решетки как решетки компактных открытых множеств некоторых топологических пространств . Этот результат можно рассматривать как обобщение знаменитой теоремы Стоуна о представлении булевых алгебр , так и как специализацию общего положения двойственности Стоуна .

Еще одно важное представление было установлено Хилари Пристли в ее теореме о представлении дистрибутивных решеток . В этой формулировке дистрибутивная решетка используется для построения топологического пространства с дополнительным частичным порядком в его точках, что дает (полностью разделенное по порядку) упорядоченное пространство Стоуна (или пространство Пристли ). Исходная решетка восстанавливается как совокупность открытозамкнутых нижних множеств этого пространства.

Вследствие теорем Стоуна и Пристли легко увидеть, что любая дистрибутивная решетка действительно изоморфна решетке множеств. Однако для доказательства обоих утверждений требуется булева теорема о простых идеалах , слабая форма аксиомы выбора .

Свободные распределительные решетки

Свободные дистрибутивные решетки с нулевым, одним, двумя и тремя образующими. Элементы с метками «0» и «1» представляют собой пустое соединение и встречу, а элемент с меткой «большинство» равен ( x ∧ y ) ∨ ( x ∧ z ) ∨ ( y ∧ z ) = ( x ∨ y ) ∧ ( Икс ∨ z ) ∧ ( y ∨ z ).

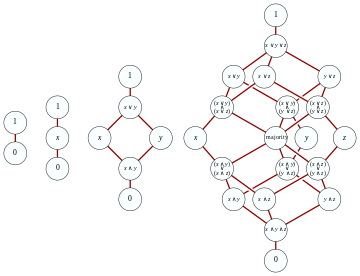
Свободную дистрибутивную решетку над множеством образующих G можно построить гораздо проще, чем общую свободную решетку . Первое наблюдение состоит в том, что, используя законы дистрибутивности, каждый член, образованный бинарными операциями и набором образующих, может быть преобразован в следующую эквивалентную нормальную форму : ${\displaystyle \lor }$ ${\displaystyle \land }$

${\displaystyle M_{1}\lor M_{2}\lor \cdots \lor M_{n},}$

где – конечные множества элементов G . Более того, поскольку и встречи, и соединения являются ассоциативными , коммутативными и идемпотентными , можно игнорировать дубликаты и порядок и представлять объединение встреч, подобное приведенному выше, как набор наборов: ${\displaystyle M_{i}}$

${\displaystyle \{N_{1},N_{2},\ldots ,N_{n}\},}$

где – конечные подмножества G . Однако все же возможно, что два таких термина обозначают один и тот же элемент дистрибутивной решетки. Это происходит, когда существуют индексы j и k , которые являются подмножеством. В этом случае совпадение будет ниже пересечения, и, следовательно, можно безопасно удалить избыточный набор , не меняя интерпретации всего термина. Следовательно, множество конечных подмножеств G будем называть неизбыточным , если все его элементы взаимно несравнимы (относительно порядка подмножества); то есть когда оно образует антицепь конечных множеств . ${\displaystyle N_{i}}$ ${\displaystyle N_{j}}$ ${\displaystyle N_{k}.}$ ${\displaystyle N_{k}}$ ${\displaystyle N_{j},}$ ${\displaystyle N_{k}}$ ${\displaystyle N_{i}}$

Теперь свободная дистрибутивная решетка над множеством образующих G определена на множестве всех конечных неизбыточных множеств конечных подмножеств G . Соединение двух конечных неизбыточных множеств получается их объединением удалением всех избыточных множеств. Точно так же встреча двух множеств S и T является неизбыточной версией. Проверка того, что эта структура является дистрибутивной решеткой с требуемым универсальным свойством, является рутинной. ${\displaystyle \{N\cup M\mid N\in S,M\in T\}.}$

Число элементов в свободных дистрибутивных решетках с n образующими определяется числами Дедекинда . Эти числа быстро растут и известны только для n  ≤ 9; они есть

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, 286386577668298411128469151667598498812366 (последовательность A000 372 в OEIS ).

Числа, приведенные выше, подсчитывают количество элементов в свободных дистрибутивных решетках, в которых операции решетки представляют собой соединения и встречи конечных наборов элементов, включая пустое множество. Если пустые соединения и пустые встречи запрещены, в результирующих свободных распределительных решетках будет на два элемента меньше; их количество элементов образует последовательность

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786, 286386577668298411128469151667598498812364 (последовательность A007 153 в OEIS ).

Смотрите также

• Полностью дистрибутивная решетка - решетка, в которой бесконечные соединения распределяются по бесконечным узлам.
• Теория двойственности дистрибутивных решеток
• Спектральное пространство

Рекомендации

1. Биркгоф, Гаррет (1967). Теория решетки . Публикации коллоквиума (3-е изд.). Американское математическое общество. п. 11. ISBN 0-8218-1025-1.§6, Теорема 9
2. Фельснер, Стефан; Кнауэр, Коля (2011), «Дистрибутивные решетки, многогранники и обобщенные потоки», Европейский журнал комбинаторики , 32 (1): 45–59, doi : 10.1016/j.ejc.2010.07.011 , MR  2727459.
3. Пирс, Чарльз С .; Фиш, Миннесота; Клозель, CJW (1989), Сочинения Чарльза С. Пирса: 1879–1884, Издательство Индианского университета, п. XLII.
4. Чарльз С. Пирс (1880). «Об алгебре логики». Американский журнал математики . 3 : 15–57. дои : 10.2307/2369442. JSTOR  2369442., п. 33 снизу
5. А. Корсельт (1894). «Bemerkung zur Algebra der Logik». Математические Аннален . 44 : 156–157. дои : 10.1007/bf01446978.Пример недистрибутивной решетки Корсельта представляет собой вариант M ₃ , где 0, 1 и x , y , z соответствуют пустому множеству, линии и трем различным точкам на нем соответственно.
6. Балбес и Двингер (1975), с. 63 со ссылкой на Биркгофа Г. «Подпрямые объединения в универсальной алгебре», Bull. амер. Математика. Соц. Т.О. (1944), 764-768.
7. См. теорему Биркгофа о представлении # Частичный порядок соединения-неприводимых .
8. Биркгоф, Гарретт ; Кисс, С.А. (1947), «Трнарная операция в распределительных решетках», Бюллетень Американского математического общества , 53 (1): 749–752, doi : 10.1090/S0002-9904-1947-08864-9 , MR  0021540.

дальнейшее чтение

• Беррис, Стэнли Н.; Санкаппанавар, HP (1981). Курс универсальной алгебры. Спрингер-Верлаг. ISBN 3-540-90578-2.
• Последовательность OEIS A006982 (Количество непомеченных дистрибутивных решеток с n элементами)