

В 3D компьютерной графике излучательность — это применение метода конечных элементов для решения уравнения рендеринга для сцен с поверхностями, которые диффузно отражают свет . В отличие от методов рендеринга , которые используют алгоритмы Монте-Карло (например, трассировка пути ), которые обрабатывают все типы световых путей, типичная излучательность учитывает только пути (представленные кодом «LD*E»), которые покидают источник света и отражаются диффузно некоторое количество раз (возможно, ноль) перед тем, как попасть в глаз. Излучательность — это алгоритм глобального освещения в том смысле, что освещение, падающее на поверхность, исходит не только непосредственно от источников света, но и от других поверхностей, отражающих свет. Излучательность не зависит от точки обзора, что увеличивает объем необходимых вычислений, но делает их полезными для всех точек обзора.
Методы излучения были впервые разработаны около 1950 года в области инженерии теплопередачи . Позднее они были усовершенствованы специально для проблемы рендеринга компьютерной графики в 1984–1985 годах исследователями из Корнеллского университета [2] и Хиросимского университета [3] .
Известными коммерческими движками радиационизма являются Enlighten от Geomerics (используется в таких играх, как Battlefield 3 и Need for Speed: The Run ); 3ds Max ; form•Z ; LightWave 3D и Electric Image Animation System .
Включение расчетов излучательности в процесс рендеринга часто придает дополнительный элемент реализма готовой сцене, поскольку она имитирует явления реального мира. Рассмотрим простую сцену комнаты.
Изображение слева было визуализировано с помощью типичного рендерера прямого освещения . В этой сцене есть три типа освещения, которые были специально выбраны и размещены художником в попытке создать реалистичное освещение: точечное освещение с тенями (размещено за окном, чтобы создать свет, падающий на пол), окружающее освещение (без которого любая часть комнаты, не освещенная напрямую источником света, была бы полностью темной) и всенаправленное освещение без теней (чтобы уменьшить плоскость окружающего освещения).
Изображение справа было визуализировано с помощью алгоритма излучательности . Есть только один источник света : изображение неба, размещенное за окном. Разница заметна. Комната светится светом. Мягкие тени видны на полу, и тонкие световые эффекты заметны по всей комнате. Более того, красный цвет с ковра перетек на серые стены, придав им слегка теплый вид. Ни один из этих эффектов не был специально выбран или разработан художником.
Поверхности сцены, которые должны быть визуализированы, делятся каждая на одну или несколько меньших поверхностей (патчей). Для каждой пары патчей вычисляется фактор вида (также известный как форм-фактор ); это коэффициент, описывающий, насколько хорошо патчи могут видеть друг друга. Патчи, которые находятся далеко друг от друга или ориентированы под косыми углами относительно друг друга, будут иметь меньшие факторы вида. Если на пути находятся другие патчи, фактор вида будет уменьшен или равен нулю, в зависимости от того, является ли окклюзия частичной или полной.
Факторы вида используются как коэффициенты в линейной системе уравнений рендеринга. Решение этой системы дает излучательность, или яркость, каждого патча, принимая во внимание диффузные взаимные отражения и мягкие тени.
Прогрессивное излучение решает систему итеративно с промежуточными значениями излучения для патча, соответствующими уровням отскока. То есть после каждой итерации мы знаем, как выглядит сцена после одного отражения света, после двух проходов, двух отражений и т. д. Это полезно для получения интерактивного предварительного просмотра сцены. Кроме того, пользователь может остановить итерации, как только изображение станет выглядеть достаточно хорошо, а не ждать, пока вычисление численно сойдется.

Другим распространенным методом решения уравнения излучательности является «стреляющая излучательность», которая итеративно решает уравнение излучательности, «стреляя» светом из пятна с наибольшей энергией на каждом шаге. После первого прохода будут освещены только те пятна, которые находятся в прямой видимости излучающего свет пятна. После второго прохода будет освещено больше пятен, поскольку свет начинает отражаться от сцены. Сцена продолжает становиться ярче и в конечном итоге достигает устойчивого состояния.
Базовый метод излучения основан на теории теплового излучения , поскольку излучение основано на вычислении количества световой энергии, передаваемой между поверхностями. Для упрощения вычислений метод предполагает, что все рассеяние является идеально диффузным . Поверхности обычно дискретизируются на четырехугольные или треугольные элементы, над которыми определяется кусочно-полиномиальная функция.
После этого разложения количество передаваемой световой энергии может быть вычислено с использованием известной отражательной способности отражающего пятна в сочетании с коэффициентом обзора двух пятен. Эта безразмерная величина вычисляется из геометрической ориентации двух пятен и может рассматриваться как доля общей возможной излучающей площади первого пятна, которая покрыта вторым.
Точнее, излучательность B — это энергия на единицу площади, покидающая поверхность пятна за дискретный интервал времени, и представляет собой комбинацию излучаемой и отраженной энергии:
где:
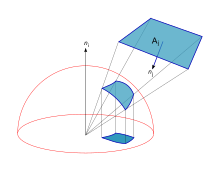
Если поверхности аппроксимируются конечным числом плоских участков, каждый из которых имеет постоянную излучательность B i и отражательную способность ρ i , то приведенное выше уравнение дает дискретное уравнение излучательности,
где F ij — геометрический коэффициент обзора для излучения, выходящего из j и падающего на участок i .
Это уравнение затем можно применить к каждому патчу. Уравнение является монохроматическим, поэтому цветовая визуализация излучения требует расчета для каждого из требуемых цветов.
Уравнение можно формально решить как матричное уравнение, чтобы получить векторное решение:
Это дает полное решение "бесконечного отскока" для B напрямую. Однако количество вычислений для вычисления матричного решения масштабируется в соответствии с n 3 , где n — количество патчей. Это становится недопустимым для реалистично больших значений n .
Вместо этого уравнение можно проще решить итеративно, многократно применяя приведенную выше формулу обновления с одним отскоком. Формально это решение матричного уравнения с помощью итерации Якоби . Поскольку отражательные способности ρ i меньше 1, эта схема быстро сходится, обычно требуя лишь нескольких итераций для получения разумного решения. Также можно использовать другие стандартные итерационные методы для решений матричных уравнений, например, метод Гаусса–Зейделя , где обновленные значения для каждого патча используются в расчете сразу после их вычисления, а не все обновляются синхронно в конце каждого развертки. Решение также можно настроить для итерации по каждому из отправляющих элементов по очереди в его основном внешнем цикле для каждого обновления, а не для каждого из принимающих патчей. Это известно как вариант алгоритма стрельбы , в отличие от варианта сбора . Используя взаимность фактора обзора, A i F ij = A j F ji , уравнение обновления также можно переписать в терминах фактора обзора F ji , видимого каждым отправляющим патчем A j :
Иногда это называют формулировкой «мощности», поскольку теперь обновляется общая передаваемая мощность каждого элемента, а не его излучательность.
Фактор вида F ij сам по себе может быть вычислен несколькими способами. Ранние методы использовали полукуб (воображаемый куб с центром на первой поверхности, на которую проецировалась вторая поверхность, разработанный Майклом Ф. Коэном и Дональдом П. Гринбергом в 1985 году). Поверхность полукуба была разделена на пикселеподобные квадраты, для каждого из которых фактор вида можно было легко вычислить аналитически. Полный форм-фактор затем можно было аппроксимировать, суммируя вклад каждого из пикселеподобных квадратов. Проекция на полукуб, которую можно было адаптировать из стандартных методов определения видимости многоугольников, также решала проблему промежуточных участков, частично скрывающих те, что находятся позади.
Однако все это было довольно затратно с точки зрения вычислений , поскольку в идеале форм-факторы должны быть получены для каждой возможной пары патчей, что приводит к квадратичному увеличению вычислений по мере увеличения числа патчей. Это можно несколько уменьшить, используя двоичное дерево разбиения пространства , чтобы сократить время, затрачиваемое на определение того, какие патчи полностью скрыты от других в сложных сценах; но даже в этом случае время, затрачиваемое на определение форм-фактора, все еще обычно масштабируется как n log n . Новые методы включают адаптивную интеграцию. [4]
Факторы формы F ij сами по себе на самом деле явно не нужны ни в одном из уравнений обновления; ни для оценки полной интенсивности Σ j F ij B j , собранной из всего вида, ни для оценки того, как распределяется излучаемая мощность A j B j . Вместо этого эти обновления можно оценить с помощью методов выборки, без необходимости явно рассчитывать факторы формы. С середины 1990-х годов такие подходы выборки были методами, наиболее часто используемыми для практических расчетов излучательности.
Собранную интенсивность можно оценить, создав набор образцов в единичной окружности, подняв их на полусферу, а затем посмотрев, какова была излучательность элемента, на котором возник бы луч, входящий в этом направлении. Оценка общей собранной интенсивности тогда является просто средним из излучательностей, обнаруженных каждым лучом. Аналогично, в формулировке мощности мощность можно распределить, создав набор лучей из излучающего элемента таким же образом и распределив мощность так, чтобы она была распределена поровну между каждым элементом, на который попадает луч.
Это по сути то же самое распределение, которое программа трассировки пути будет сэмплировать при трассировке назад одного шага диффузного отражения; или которое программа двунаправленной трассировки лучей будет сэмплировать для достижения одного шага прямого диффузного отражения при отображении источника света вперед. Таким образом, подход сэмплирования в некоторой степени представляет собой конвергенцию между двумя методами, ключевым отличием остается то, что метод излучательности направлен на построение достаточно точной карты сияния всех поверхностей в сцене, а не просто на представление текущего вида.
Хотя в своей базовой форме предполагается, что излучательность имеет квадратичное увеличение времени вычислений с добавленной геометрией (поверхностями и патчами), это не обязательно так. Проблему излучательности можно перефразировать как проблему рендеринга сцены с текстурным отображением . В этом случае время вычислений увеличивается только линейно с количеством патчей (игнорируя сложные вопросы, такие как использование кэша ).
Следуя за коммерческим энтузиазмом в отношении изображений с улучшенной излучательностью, но до стандартизации быстрого расчета излучательности, многие архитекторы и графические художники использовали технику, которую в общих чертах называют ложной излучательностью . Затемняя области текстурных карт, соответствующие углам, [ требуется ссылка ] стыкам и углублениям, и применяя их посредством самосвечения или диффузного отображения, можно было создать эффект взаимодействия патчей, подобный излучательности, с помощью стандартного рендерера сканлайна (ср. ambient occlusion ).
Статическое, предварительно рассчитанное излучение может отображаться в реальном времени с помощью карт освещения на современных настольных компьютерах со стандартным аппаратным обеспечением для ускорения графики .

Одним из преимуществ алгоритма Radiosity является то, что его относительно просто объяснить и реализовать. Это делает его полезным алгоритмом для обучения студентов алгоритмам глобального освещения. Типичный рендерер прямого освещения уже содержит почти все алгоритмы ( перспективные преобразования , текстурное отображение , удаление скрытых поверхностей ), необходимые для реализации Radiosity. Для понимания или реализации этого алгоритма не требуется сильных математических знаний [ требуется цитата ] .
Типичные методы излучательности учитывают только световые пути формы LD*E, то есть пути, которые начинаются у источника света и совершают несколько диффузных отскоков, прежде чем достигнут глаза. Хотя существует несколько подходов к интеграции других эффектов освещения, таких как зеркальные [5] и глянцевые [6] отражения, методы, основанные на излучательности, обычно не используются для решения полного уравнения рендеринга.
Базовая излучательность также имеет проблемы с разрешением внезапных изменений видимости (например, резких теней), поскольку грубая, регулярная дискретизация в кусочно-постоянные элементы соответствует низкочастотному коробочному фильтру пространственной области. Сетка разрывов [1] использует знание событий видимости для создания более интеллектуальной дискретизации.
Radiosity был, пожалуй, первым алгоритмом рендеринга, который широко использовался и учитывал рассеянное непрямое освещение. Более ранние алгоритмы рендеринга, такие как трассировка лучей в стиле Уиттеда, могли вычислять такие эффекты, как отражения, преломления и тени, но, несмотря на то, что они были весьма глобальными явлениями, эти эффекты обычно не назывались « глобальным освещением ». В результате термины « диффузное взаимоотражение » и «radiosity» стали путать с «глобальным освещением» в просторечии . Однако эти три понятия являются разными.
Метод излучения в контексте компьютерной графики происходит от метода излучения в теплообмене (и по сути совпадает с ним) . В этом контексте излучение — это полный поток излучения (как отраженный, так и переизлученный), покидающий поверхность; это также иногда называют выходом излучения . Расчет излучения, а не температуры поверхности, является ключевым аспектом метода излучения, который позволяет применять линейные матричные методы к проблеме.