stringtranslate.com

Квантовое число

Орбитали одиночных электронов для водородоподобных атомов с квантовыми числами n = 1, 2, 3 (блоки), ℓ (строки) и m (столбцы). Спин s не виден, поскольку не имеет пространственной зависимости.

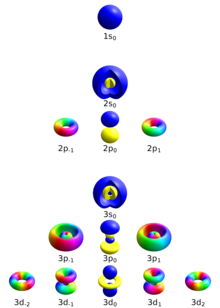
В квантовой физике и химии квантовые числа — это величины, характеризующие возможные состояния системы. Для полного определения состояния электрона в атоме водорода необходимы четыре квантовых числа. Традиционный набор квантовых чисел включает главные , азимутальные , магнитные и спиновые квантовые числа . Для описания других систем требуются другие квантовые числа. Для субатомных частиц необходимо ввести новые квантовые числа, такие как аромат кварков , которые не имеют классического соответствия.

Квантовые числа тесно связаны с собственными значениями наблюдаемых . Когда соответствующая наблюдаемая коммутирует с гамильтонианом системы , квантовое число называется « хорошим » и действует как константа движения в квантовой динамике.

История

Электронные квантовые числа

В эпоху старой квантовой теории , начиная с предложения Макса Планка о квантах в его модели излучения черного тела (1900) и адаптации Альберта Эйнштейна этой концепции для объяснения фотоэлектрического эффекта (1905), и до тех пор, пока Эрвин Шредингер не опубликовал свое уравнение собственных функций в 1926 году, [1] концепция, лежащая в основе квантовых чисел, развивалась на основе атомной спектроскопии и теорий классической механики с дополнительными специальными ограничениями. [2] : 106  Многие результаты атомной спектроскопии были обобщены в формуле Ридберга, включающей различия между двумя сериями энергий, связанными целыми шагами. Модель атома , впервые предложенная Нильсом Бором в 1913 году, опиралась на одно квантовое число. Вместе с ограничением Бора, что поглощение излучения не является классическим, она смогла объяснить часть серии Бальмера формулы атомного спектра Ридберга. [3]

Как отмечает Бор в своей последующей Нобелевской лекции, следующий шаг был сделан Арнольдом Зоммерфельдом в 1915 году . [4] Атомная модель Зоммерфельда добавила второе квантовое число и концепцию квантованных фазовых интегралов для их обоснования. [5] : 207  Модель Зоммерфельда была по сути двумерной, моделируя электрон как вращающийся в плоскости; в 1919 году он расширил свою работу до трех измерений, используя «пространственное квантование» вместо квантованных фазовых интегралов. [6] : 152  Карл Шварцшильд и ученик Зоммерфельда, Пол Эпштейн , независимо показали, что добавление третьего квантового числа дает полное объяснение результатов эффекта Штарка .

Следствием квантования пространства было то, что орбитальное взаимодействие электрона с внешним магнитным полем было бы квантовано. Это, казалось, подтвердилось, когда результаты эксперимента Штерна-Герлаха сообщили о квантованных результатах для атомов серебра в неоднородном магнитном поле. Подтверждение оказалось преждевременным: потребовалось бы больше квантовых чисел. [7]

Четвертое и пятое квантовые числа атомной эры возникли из попыток понять эффект Зеемана . Как и эксперимент Штерна-Герлаха, эффект Зеемана отражает взаимодействие атомов с магнитным полем; в слабом поле экспериментальные результаты назывались «аномальными», они расходились с любой теорией того времени. Решением Вольфганга Паули этой проблемы было введение другого квантового числа, принимающего только два возможных значения, . [8] В конечном итоге это стало квантованными значениями проекции спина , собственного кванта углового момента электрона. В 1927 году Рональд Фрейзер продемонстрировал, что квантование в эксперименте Штерна-Герлаха было обусловлено магнитным моментом, связанным со спином электрона, а не его орбитальным угловым моментом. [7] Успех Паули в разработке аргументов в пользу спинового квантового числа без опоры на классические модели подготовил почву для разработки квантовых чисел для элементарных частиц в оставшейся части 20-го века. [8]

Бор с его принципом Aufbau или «наращивания» и Паули с его принципом исключения связали электронные квантовые числа атома в структуру для предсказания свойств атомов. [9] Когда Шредингер опубликовал свое волновое уравнение и рассчитал уровни энергии водорода, эти два принципа стали основой атомной физики.

Ядерные квантовые числа

С успешными моделями атома внимание физики переключилось на модели ядра. Начиная с первоначальной модели Гейзенберга протон-нейтронной связи в 1932 году, Юджин Вигнер ввел изоспин в 1937 году, первое «внутреннее» квантовое число, не связанное с симметрией в реальном пространстве-времени. [10] : 45 

Связь с симметрией

По мере развития квантовой механики абстракция возрастала, и модели, основанные на симметрии и инвариантности, играли все большую роль. За два года до своей работы над квантовым волновым уравнением Шредингер применил идеи симметрии, созданные Эмми Нётер и Германом Вейлем , к электромагнитному полю. [11] : 198  По мере развития квантовой электродинамики в 1930-х и 1940-х годах теория групп стала важным инструментом. К 1953 году Чэнь Нин Ян был одержим идеей, что теория групп может быть применена для связи сохраняющихся квантовых чисел ядерных столкновений с симметриями в полевой теории нуклонов. [11] : 202  Совместно с Робертом Миллсом Ян разработал неабелеву калибровочную теорию, основанную на сохранении ядерных изоспиновых квантовых чисел.

Общие свойства

Хорошие квантовые числа соответствуют собственным значениям операторов , которые коммутируют с гамильтонианом , величинам, которые могут быть известны с точностью в то же время, что и энергия системы. В частности, наблюдаемые, которые коммутируют с гамильтонианом , одновременно диагонализируются с ним, и поэтому собственные значения и энергия (собственные значения гамильтониана) не ограничены соотношением неопределенности, возникающим из-за некоммутативности. Вместе спецификация всех квантовых чисел квантовой системы полностью характеризует базисное состояние системы и в принципе может быть измерена вместе. Многие наблюдаемые имеют дискретные спектры (наборы собственных значений) в квантовой механике, поэтому величины могут быть измерены только в дискретных значениях. В частности, это приводит к квантовым числам, которые принимают значения в дискретных наборах целых или полуцелых чисел ; хотя в некоторых случаях они могут приближаться к бесконечности .

Количество квантовых чисел варьируется от системы к системе и не имеет универсального ответа. Следовательно, эти параметры должны быть найдены для каждой анализируемой системы. Квантованная система требует по крайней мере одного квантового числа. Динамика (т. е. временная эволюция) любой квантовой системы описывается квантовым оператором в форме гамильтониана H . Существует одно квантовое число системы, соответствующее энергии системы; т. е. одно из собственных значений гамильтониана. Существует также одно квантовое число для каждого линейно независимого оператора O , который коммутирует с гамильтонианом. Полный набор коммутирующих наблюдаемых (CSCO), которые коммутируют с гамильтонианом, характеризует систему со всеми ее квантовыми числами. Существует взаимно-однозначное соотношение между квантовыми числами и операторами CSCO, причем каждое квантовое число принимает одно из собственных значений своего соответствующего оператора. В результате различного базиса , который может быть произвольно выбран для формирования полного набора коммутирующих операторов, различные наборы квантовых чисел могут использоваться для описания одной и той же системы в различных ситуациях.

Электрон в водородоподобном атоме

Четыре квантовых числа могут полностью описать уровень энергии электрона в водородоподобном атоме :

Эти квантовые числа также используются в классическом описании состояний ядерных частиц (например, протонов и нейтронов). [ необходима цитата ] Квантовое описание молекулярных орбиталей требует других квантовых чисел, поскольку симметрии молекулярной системы различны.

Главное квантовое число

Главное квантовое число описывает электронную оболочку электрона. Значение n варьируется от 1 до оболочки, содержащей самый внешний электрон этого атома, то есть [12]

п = 1, 2, ...

Например, в цезии (Cs) самый внешний валентный электрон находится в оболочке с энергетическим уровнем 6, поэтому электрон в цезии может иметь значение n от 1 до 6. Среднее расстояние между электроном и ядром увеличивается с n .

Азимутальное квантовое число

Азимутальное квантовое число , также известное как квантовое число орбитального углового момента , описывает подоболочку и дает величину орбитального углового момента через соотношение

L 2 = ħ 2 ℓ ( ℓ + 1).

В химии и спектроскопии ℓ = 0 называется s-орбиталью, ℓ = 1 — p-орбиталью, ℓ = 2 — d-орбиталью и ℓ = 3 — f-орбиталью.

Значение ℓ варьируется от 0 до n − 1 , поэтому первая p-орбиталь ( ℓ = 1 ) появляется во второй электронной оболочке ( n = 2 ), первая d-орбиталь ( ℓ = 2 ) появляется в третьей оболочке ( n = 3 ) и так далее: [13]

ℓ = 0, 1, 2,..., n − 1

Квантовое число, начинающееся с n = 3, ℓ = 0, описывает электрон на s-орбитали третьей электронной оболочки атома. В химии это квантовое число очень важно, поскольку оно определяет форму атомной орбитали и сильно влияет на химические связи и углы связи . Азимутальное квантовое число также может обозначать число угловых узлов, присутствующих в орбитали. Например, для p-орбиталей ℓ = 1 , и, таким образом, количество угловых узлов в p-орбитали равно 1.

Магнитное квантовое число

Магнитное квантовое число описывает конкретную орбиталь внутри подоболочки и дает проекцию орбитального углового момента вдоль указанной оси :

L z = m ℓ ħ

Значения m ℓ лежат в диапазоне от − ℓ до ℓ с целочисленными интервалами. [14] [ нужна страница ]

Подоболочка s ( ℓ = 0 ) содержит только одну орбиталь, и поэтому m ℓ электрона на s-орбитали всегда будет равен 0. Подоболочка p ( ℓ = 1 ) содержит три орбитали, поэтому m ℓ электрона на p-орбитали будет равен −1, 0 или 1. Подоболочка d ( ℓ = 2 ) содержит пять орбиталей со значениями m ℓ −2, −1, 0, 1 и 2.

Спиновое магнитное квантовое число

Спиновое магнитное квантовое число описывает собственный спиновый момент импульса электрона внутри каждой орбитали и дает проекцию спинового момента импульса S вдоль указанной оси:

S z = m s ħ .

В общем случае значения m s лежат в диапазоне от − s до s , где s — спиновое квантовое число, связанное с величиной собственного спинового углового момента частицы: [15]

м с = − с , − с + 1, − с + 2, ..., с − 2, с − 1, с .

Состояние электрона имеет спиновое число s = ⁠1/2⁠ , следовательно m s будет + ⁠1/2⁠ («раскручивать») или - ⁠1/2⁠ "спин вниз" состояния. Поскольку электроны являются фермионами , они подчиняются принципу исключения Паули : каждое состояние электрона должно иметь разные квантовые числа. Поэтому каждая орбиталь будет занята максимум двумя электронами, по одному на каждое состояние спина.

Принцип Ауфбау и правила Хунда.

Многоэлектронный атом можно качественно смоделировать как водородоподобный атом с более высоким зарядом ядра и, соответственно, большим количеством электронов. Заполнение электронных состояний в таком атоме можно предсказать с помощью принципа Ауфбау и эмпирических правил Хунда для квантовых чисел. Принцип Ауфбау заполняет орбитали на основе их главных и азимутальных квантовых чисел ( сначала самые низкие, с самыми низкими разрывными связями; правило Хунда благоприятствует неспаренным электронам на самой внешней орбитали). Эти правила являются эмпирическими, но их можно соотнести с электронной физикой. [16] : 10  [17] : 260 

Спин-орбитально связанные системы

Когда мы принимаем во внимание спин-орбитальное взаимодействие , операторы L и S больше не коммутируют с гамильтонианом , и собственные состояния системы больше не имеют четко определенных орбитального углового момента и спина. Таким образом, следует использовать другой набор квантовых чисел. Этот набор включает [18] [19]

  1. Полное квантовое число углового момента :
    j = | ℓ ± s |

    что дает полный угловой момент через соотношение

    J 2 = ħ 2 j ( j + 1)
  2. Проекция полного момента импульса вдоль заданной оси:
    м j = - j , - j + 1, - j + 2, ..., j - 2, j - 1, j

    аналогично вышеизложенному и удовлетворяет

    m j = m ℓ + m s и | m ℓ + m s | ≤ j
  3. Паритет

    Это собственное значение при отражении: положительное (+1) для состояний, которые пришли из четного ℓ и отрицательное (−1) для состояний, которые пришли из нечетного ℓ . Первое также известно как четная четность , а второе как нечетная четность , и задается как

    Р = (−1) ℓ

Например, рассмотрим следующие 8 состояний, определяемые их квантовыми числами:

Квантовые состояния в системе можно описать как линейную комбинацию этих 8 состояний . Однако, при наличии спин-орбитального взаимодействия , если кто-то хочет описать ту же систему 8 состояниями, которые являются собственными векторами гамильтониана (т.е. каждое представляет собой состояние, которое не смешивается с другими с течением времени), мы должны рассмотреть следующие 8 состояний:

Атомные ядра

В ядрах вся совокупность протонов и нейтронов ( нуклонов ) имеет результирующий угловой момент, обусловленный угловыми моментами каждого нуклона, обычно обозначаемый I. Если полный угловой момент нейтрона равен j n = ℓ + s , а для протона равен j p = ℓ + s (где s для протонов и нейтронов оказывается равным ⁠1/2⁠ снова ( см. примечание )), то квантовые числа ядерного углового момента I определяются как:

Я = | j n − j p |, | j n − j p | + 1, | j n − j p | + 2, ..., ( j n + j p ) − 2, ( j n + j p ) − 1, ( j n + j p )

Примечание: Орбитальные угловые моменты ядерных (и атомных) состояний являются целыми кратными ħ, тогда как собственные угловые моменты нейтрона и протона являются полуцелыми кратными. Должно быть сразу очевидно, что комбинация собственных спинов нуклонов с их орбитальным движением всегда будет давать полуцелые значения для полного спина, I , любого нечетного ядра A и целые значения для любого четного ядра A.

Четность с числом I используется для обозначения состояний ядерного углового момента, примерами для некоторых изотопов водорода (H), углерода (C) и натрия (Na) являются: [20]

Причина необычных флуктуаций в I , даже при различиях всего в один нуклон, обусловлена ​​нечетным и четным числом протонов и нейтронов — пары нуклонов имеют полный угловой момент, равный нулю (как и электроны на орбиталях), оставляя нечетное или четное число неспаренных нуклонов. Свойство ядерного спина является важным фактором для работы ЯМР- спектроскопии в органической химии , [19] и МРТ в ядерной медицине , [20] из-за ядерного магнитного момента, взаимодействующего с внешним магнитным полем .

Элементарные частицы

Элементарные частицы содержат много квантовых чисел, которые обычно считаются присущими им. Однако следует понимать, что элементарные частицы являются квантовыми состояниями стандартной модели физики элементарных частиц , и, следовательно, квантовые числа этих частиц имеют такое же отношение к гамильтониану этой модели, как квантовые числа атома Бора к его гамильтониану . Другими словами, каждое квантовое число обозначает симметрию задачи. В квантовой теории поля более полезно различать пространственно-временные и внутренние симметрии.

Типичные квантовые числа, связанные с симметриями пространства-времени, — это спин (связанный с вращательной симметрией), четность , C-четность и T-четность (связанные с симметрией Пуанкаре пространства -времени ). Типичные внутренние симметрии [ требуется разъяснение ] — это лептонное число и барионное число или электрический заряд . (Полный список квантовых чисел такого рода см. в статье flavor .)

Мультипликативные квантовые числа

Большинство сохраняющихся квантовых чисел являются аддитивными, поэтому в реакции элементарной частицы сумма квантовых чисел должна быть одинаковой до и после реакции. Однако некоторые, обычно называемые четностью , являются мультипликативными; т. е. их произведение сохраняется. Все мультипликативные квантовые числа принадлежат симметрии (например, четности), в которой применение преобразования симметрии дважды эквивалентно ничегонеделанию ( инволюции ).

Смотрите также

Ссылки

  1. ^ Шредингер, Эрвин (1926). «Квантование как проблема собственных значений». Аннален дер Физик . 81 (18): 109–139. Бибкод : 1926АнП...386..109С. дои : 10.1002/andp.19263861802.
  2. ^ Уиттекер, Эдмунд Т. (1989). История теорий эфира и электричества. 2: Современные теории, 1900 - 1926 (переиздание). Нью-Йорк: Dover Publ. ISBN 978-0-486-26126-3.
  3. ^ Хейлброн, Джон Л. (июнь 2013 г.). «Путь к квантовому атому». Nature . 498 (7452): 27–30. doi :10.1038/498027a. ISSN  0028-0836. PMID  23739408.
  4. ^ Нильс Бор – Нобелевская лекция. NobelPrize.org. Nobel Prize Outreach AB 2024. Воскресенье, 25 февраля 2024 г.
  5. ^ Эккерт, Майкл; Эккерт, Майкл; Артин, Том (2013). Арнольд Зоммерфельд: наука, жизнь и неспокойные времена 1868-1951 гг . Нью-Йорк: Спрингер. ISBN 978-1-4614-7461-6.
  6. ^ Краг, Хельге (2012-05-17). Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925. Oxford University Press. doi :10.1093/acprof:oso/9780199654987.003.0004. ISBN 978-0-19-965498-7.
  7. ^ ab Фридрих, Бржетислав; Хершбах, Дадли (2003-12-01). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику». Physics Today . 56 (12): 53–59. Bibcode : 2003PhT....56l..53F. doi : 10.1063/1.1650229. ISSN  0031-9228.
  8. ^ ab Giulini, Domenico (2008-09-01). «Спин электрона или «классически неописуемая двузначность»». Исследования по истории и философии науки Часть B: Исследования по истории и философии современной физики . 39 (3): 557–578. arXiv : 0710.3128 . Bibcode :2008SHPMP..39..557G. doi :10.1016/j.shpsb.2008.03.005. hdl :11858/00-001M-0000-0013-13C8-1. ISSN  1355-2198.
  9. ^ Краг, Хельге (2012-05-17). Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925. Oxford University Press. doi :10.1093/acprof:oso/9780199654987.003.0007. ISBN 978-0-19-965498-7.
  10. ^ Браун, Л. М. (1988). "Заметки об истории изоспина". В Winter, Клаус; Телегди, Валентин Л. (ред.). Festi-Val: Праздничный сборник для Вала Телегди; эссе по физике в честь его 65-летия; [симпозиум ... состоялся в ЦЕРНе, Женева, 6 июля 1987 г.] . Амстердам: North-Holland Physics Publ. ISBN 978-0-444-87099-5.
  11. ^ ab Baggott, JE (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Oxford Univ. Press. ISBN 978-0-19-956684-6.
  12. ^ Бейзер, А. (1987). Концепции современной физики (4-е изд.). McGraw-Hill (International). ISBN 0-07-100144-1.[ нужна страница ]
  13. ^ Аткинс, П. В. (1977). Молекулярная квантовая механика, части I и II: Введение в квантовую химию . Том 1. Oxford University Press. ISBN 0-19-855129-0.[ нужна страница ]
  14. ^ Эйсберг и Резник 1985.
  15. ^ Пелег, Ю.; Пнини, Р.; Заарур, Э.; Хехт, Э. (2010). Квантовая механика . Очерки Шуама (2-е изд.). МакГроу Хилл (США). ISBN 978-0-07-162358-2.[ нужна страница ]
  16. ^ Джолли, Уильям Л. (1984). Современная неорганическая химия (1-е изд.). McGraw-Hill. стр. 10–12. ISBN 0-07-032760-2.
  17. ^ Левин, Айра Н. (1983). Физическая химия (2-е изд.). Нью-Йорк: McGraw-Hill. ISBN 978-0-07-037421-8.
  18. ^ Аткинс, П. В. (1977). Молекулярная квантовая механика, части I и II: Введение в квантовую химию . Том 1. Oxford University Press. ISBN 0-19-855129-0.[ нужна страница ]
  19. ^ ab Atkins, PW (1977). Молекулярная квантовая механика Часть III: Введение в квантовую химию . Том 2. Oxford University Press.[ ISBN отсутствует ] [ нужна страница ]
  20. ^ ab Krane, KS (1988). Введение в ядерную физику . John Wiley & Sons. ISBN 978-0-471-80553-3.[ нужна страница ]

Дальнейшее чтение