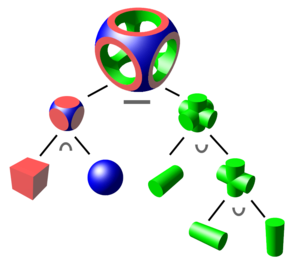
Конструктивная геометрия твердого тела ( CSG ; ранее называлась вычислительной бинарной геометрией твердого тела ) — это метод, используемый в моделировании твердого тела . Конструктивная геометрия твердого тела позволяет моделеру создавать сложную поверхность или объект, используя булевы операторы для объединения более простых объектов, [1] потенциально создавая визуально сложные объекты путем объединения нескольких примитивных. [2] [3]
В 3D компьютерной графике и САПР CSG часто используется в процедурном моделировании . CSG также может выполняться на полигональных сетках и может быть или не быть процедурным и/или параметрическим.
Сравните CSG с моделированием полигональной сетки и моделированием коробок .
Простейшие твердые объекты, используемые для представления, называются геометрическими примитивами . Обычно это объекты простой формы: кубоиды , цилиндры , призмы , пирамиды , сферы , конусы . [1] Набор допустимых примитивов ограничен каждым программным пакетом. Некоторые программные пакеты допускают CSG на изогнутых объектах, а другие — нет.
Объект создается из примитивов с помощью допустимых операций , которые обычно представляют собой булевы операции над множествами : объединение , пересечение и разность , а также геометрические преобразования этих множеств. [1]
Примитив обычно может быть описан процедурой , которая принимает некоторое количество параметров ; например, сфера может быть описана координатами ее центральной точки вместе со значением радиуса. Эти примитивы могут быть объединены в составные объекты с помощью операций, подобных этим:
Комбинируя эти элементарные операции, можно создавать объекты высокой сложности, начиная с простых.
Визуализация конструктивной твердотельной геометрии особенно проста при трассировке лучей . Трассировщики лучей пересекают луч с обоими примитивами, над которыми выполняется операция, применяют оператор к интервалам пересечения вдоль одномерного луча, а затем берут в качестве результата точку, ближайшую к камере вдоль луча.

Конструктивная геометрия тел имеет ряд практических применений. Она используется в случаях, когда требуются простые геометрические объекты, [ требуется ссылка ] или когда важна математическая точность. [4] Почти все инженерные пакеты САПР используют CSG (где это может быть полезно для представления резов инструмента и элементов, где детали должны подходить друг другу).
Эту систему используют движки Quake и Unreal Engine, а также Hammer ( собственный редактор уровней движка Source ) и Torque Game Engine / Torque Game Engine Advanced . CSG популярен, потому что разработчик моделей может использовать набор относительно простых объектов для создания очень сложной геометрии. [3] Когда CSG является процедурным или параметрическим, пользователь может пересматривать свою сложную геометрию, изменяя положение объектов или изменяя булеву операцию, используемую для объединения этих объектов.
Одним из преимуществ CSG является то, что он может легко гарантировать, что объекты являются «твердыми» или водонепроницаемыми, если все примитивные формы являются водонепроницаемыми. [5] Это может быть важно для некоторых производственных или инженерных вычислительных приложений. Для сравнения, при создании геометрии на основе граничных представлений требуются дополнительные топологические данные или должны быть выполнены проверки согласованности, чтобы гарантировать, что данное граничное описание определяет допустимый твердый объект. [1]
Удобным свойством форм CSG является то, что легко классифицировать произвольные точки как находящиеся внутри или снаружи формы, созданной CSG. Точка просто классифицируется по всем базовым примитивам, и полученное логическое выражение оценивается. [6] Это желательное качество для некоторых приложений, таких как трассировка лучей . [6]
Поскольку модели CSG параметризуются по конструкции, они часто оказываются предпочтительнее обычных сеток , когда речь идет о приложениях, где целью является изготовление индивидуальных моделей. Для таких приложений может быть интересно преобразовать уже существующие сетки в деревья CSG. Эта проблема автоматического преобразования сеток в деревья CSG называется обратным CSG .
Результирующее дерево CSG должно занимать тот же объем в трехмерном пространстве, что и входная сетка, при этом имея минимальное количество узлов. Простые решения предпочтительны, чтобы гарантировать, что результирующая модель будет легко редактироваться. Решение этой проблемы является сложной задачей из-за большого пространства поиска, которое необходимо исследовать. Оно объединяет непрерывные параметры, такие как размер и размер примитивных форм, и дискретные параметры, такие как булевы операторы, используемые для построения окончательного дерева CSG.
Дедуктивные методы решают эту проблему, строя набор полупространств , описывающих внутреннюю часть геометрии. Эти полупространства используются для описания примитивов, которые можно объединить для получения окончательной модели. [7]
Другой подход разделяет обнаружение примитивных форм и вычисление дерева CSG, которое определяет окончательную модель. Этот подход использует способность современных инструментов синтеза программ находить дерево CSG с минимальной сложностью. [8]
Существуют также подходы, которые используют генетические алгоритмы для итеративной оптимизации начальной формы в направлении формы желаемой сетки. [9]