
Косоугольная проекция — это простой тип технического чертежа графической проекции, используемый для создания двумерных (2D) изображений трехмерных (3D) объектов.
Объекты не находятся в перспективе и поэтому не соответствуют ни одному виду объекта, который можно получить на практике, но этот метод дает довольно убедительные и полезные результаты.
Косая проекция обычно используется в техническом черчении. Кавальерная проекция использовалась французскими военными художниками в XVIII веке для изображения укреплений.
Косая проекция использовалась практически повсеместно китайскими художниками с I или II века до XVIII века, особенно для изображения прямолинейных объектов, таких как дома. [1]
Различные методы графического проецирования могут использоваться в компьютерной графике, в том числе в системах автоматизированного проектирования (САПР), компьютерных играх, компьютерной анимации и спецэффектах, используемых в фильмах.




Косая проекция — это разновидность параллельной проекции :
В косой проекции и ортографической проекции параллельные линии исходного объекта создают параллельные линии в проецируемом изображении. Проекторы в косой проекции пересекают плоскость проекции под косым углом для создания проецируемого изображения, в отличие от перпендикулярного угла, используемого в ортографической проекции.
Математически параллельная проекция точки на плоскость дает . Константы и однозначно определяют параллельную проекцию. Когда , проекция называется «ортографической» или «ортогональной». В противном случае она «косой». Константы и не обязательно меньше 1, и, как следствие, длины, измеренные на косой проекции, могут быть как больше, так и меньше, чем они были в пространстве. В общей косой проекции сферы пространства проецируются как эллипсы на плоскость чертежа, а не как круги, как они выглядели бы из ортогональной проекции.
Наклонное рисование также является самым грубым методом «3D» рисования, но самым простым в освоении. Один из способов рисования с использованием наклонного вида — нарисовать сторону объекта, на которую вы смотрите, в двух измерениях, т. е. плоской, а затем нарисовать другие стороны под углом 45°, но вместо того, чтобы рисовать стороны в полный размер, они рисуются только с половиной глубины, создавая «вынужденную глубину» — добавляя элемент реализма к объекту. Даже с этой «вынужденной глубиной» наклонные рисунки выглядят очень неубедительно для глаза. По этой причине наклонные редко используются профессиональными дизайнерами или инженерами.
В косоугольном графическом рисунке углы, отображаемые между осями, а также факторы ракурса (масштаб) являются произвольными. Точнее, любой заданный набор из трех копланарных сегментов, исходящих из одной и той же точки, может быть истолкован как образующий некоторую косую перспективу трех сторон куба. Этот результат известен как теорема Польке , по имени немецкого математика Польке, который опубликовал ее в начале 19 века. [2]
Получающиеся искажения делают эту технику непригодной для формальных рабочих чертежей. Тем не менее, искажения частично устраняются путем выравнивания одной плоскости изображения параллельно плоскости проекции. Это создает истинное изображение формы выбранной плоскости. Эта специфическая категория косых проекций, в которой длины вдоль направлений и сохраняются, но длины вдоль направления рисуются под углом с использованием коэффициента уменьшения, очень часто используется для промышленных чертежей.
В кавалерийской проекции (иногда кавалерийской перспективе или высокой точке обзора ) точка объекта представлена тремя координатами, x , y и z . На чертеже она представлена только двумя координатами, x″ и y″ . На плоском чертеже две оси, x и z на рисунке, перпендикулярны , а длина по этим осям нарисована в масштабе 1:1; таким образом, это похоже на диметрические проекции , хотя это не аксонометрическая проекция , так как третья ось, здесь y , нарисована по диагонали, образуя произвольный угол с осью x″ , обычно 30 или 45°. Длина третьей оси не масштабируется. [5] [6]
Его очень легко рисовать, особенно ручкой и бумагой. Поэтому его часто используют, когда фигуру нужно нарисовать от руки, например, на доске (урок, устный экзамен).
Первоначально это изображение использовалось для обозначения военных укреплений . На французском языке «кавалер» (буквально всадник, конник , см. Кавалерия ) — искусственный холм за стенами, позволяющий видеть противника над стенами. [7] Кавалерийская перспектива — это то, как предметы видны с этой высокой точки. Некоторые также объясняют название тем, что таким образом всадник мог видеть небольшой объект на земле со своей лошади. [8]
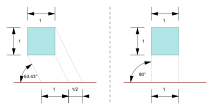
Термин проекция кабинета происходит от его использования в иллюстрациях мебельной промышленности. [9] Как и в перспективе кавалера, одна грань проецируемого объекта параллельна плоскости просмотра, а третья ось проецируется как уходящая под углом (обычно atan(2) или около ~63,4°). В отличие от проекции кавалера, где третья ось сохраняет свою длину, при проекции кабинета длина отступающих линий сокращается вдвое.
В качестве формулы можно привести такой пример: если плоскость, обращенная к наблюдателю, обозначена как xy , а отдаляющая ось — как z , то точка P проецируется следующим образом:
Где находится упомянутый угол.
Матрица преобразования имеет вид:
В качестве альтернативы можно было бы удалить одну треть от ведущего плеча, выступающего за пределы стартовой грани, что дало бы тот же результат.
В военной проекции углы осей x и z и осей y и z составляют 45°, что означает, что угол между осью x и осью y составляет 90°. То есть плоскость xy не перекошена. Однако она повернута на 45°. [10]
Помимо технического рисунка и иллюстраций, видеоигры (особенно те, которые предшествовали появлению 3D-игр) также часто используют форму косой проекции. Примерами служат SimCity , Ultima VII , Ultima Online , EarthBound , Paperboy и, совсем недавно, Tibia .