Отношение шансов

Статистика, количественно определяющая связь между двумя событиями

Отношение шансов ( OR ) — это статистика , которая количественно определяет силу связи между двумя событиями, A и B. Отношение шансов определяется как отношение шансов события A, происходящего при наличии B, к шансам события A при отсутствии B. В силу симметрии отношение шансов обратно вычисляет отношение шансов события B, происходящего при наличии A, к шансам события B при отсутствии A. Два события являются независимыми тогда и только тогда, когда OR равно 1, т. е. шансы одного события одинаковы как при наличии, так и при отсутствии другого события. Если OR больше 1, то A и B связаны (коррелированы) в том смысле, что по сравнению с отсутствием B наличие B увеличивает шансы A, и симметрично наличие A увеличивает шансы B. И наоборот, если OR меньше 1, то A и B отрицательно коррелируют, и наличие одного события уменьшает шансы наступления другого события.

Обратите внимание, что отношение шансов симметрично в двух событиях, и не подразумевается причинно-следственной связи (корреляция не подразумевает причинно-следственную связь ): OR больше 1 не устанавливает, что B вызывает A или что A вызывает B. ^[1]

Две похожие статистики, которые часто используются для количественной оценки ассоциаций, — это относительный риск (RR) и снижение абсолютного риска (ARR). Часто наибольший интерес представляет параметр RR, который представляет собой отношение вероятностей, аналогичное шансам, используемым в OR. Однако имеющиеся данные часто не позволяют вычислить RR или ARR, но позволяют вычислить OR, как в исследованиях случай-контроль , как объясняется ниже. С другой стороны, если одно из свойств (A или B) достаточно редкое (в эпидемиологии это называется предположением о редкости заболевания ), то OR приблизительно равен соответствующему RR.

OR играет важную роль в логистической модели .

Определение и основные свойства

Интуиция из примера для неспециалистов

Если мы подбросим неискаженную монету, вероятность выпадения орла и вероятность выпадения решки будут равны — обе по 50%. Представьте, что мы получим неискаженную монету, которая делает вероятность выпадения орла в два раза выше. Но что означает «вдвое больше вероятности» с точки зрения вероятности? Это не может буквально означать удвоение исходного значения вероятности, потому что удвоение 50% даст 100%. Скорее, удваиваются шансы : с шансов 1:1 до шансов 2:1. Новые вероятности составят 66⅔% для орла и 33⅓% для решки.

Мотивирующий пример в контекстепредположение о редком заболевании

Предположим, что утечка радиации в деревне с населением 1000 человек увеличила частоту возникновения редкого заболевания. Общее число людей, подвергшихся воздействию радиации, составило 1 , из которых развилась болезнь и остались здоровыми. Общее число людей, не подвергшихся воздействию, составило 1 , из которых развилась болезнь и остались здоровыми. Мы можем организовать это в виде таблицы сопряженности : ${\displaystyle V_{E}=400,}$ ${\displaystyle D_{E}=20}$ ${\displaystyle H_{E}=380}$ ${\displaystyle V_{N}=600,}$ ${\displaystyle D_{N}=6}$ ${\displaystyle H_{N}=594}$

${\displaystyle {\begin{array}{|r|cc|}\hline &{\text{ Diseased }}&{\text{ Healthy }}\\\hline {\text{ Exposed }}&20&380\\{\text{ Not exposed }}&6&594\\\hline \end{array}}}$

Риск развития заболевания при воздействии составляет , а риск развития заболевания при невоздействии составляет . Один очевидный способ сравнить риски — использовать соотношение этих двух факторов, относительный риск . ${\displaystyle D_{E}/V_{E}=20/400=.05}$ ${\displaystyle D_{N}/V_{N}=6/600=.01}$

${\displaystyle {\text{Relative risk}}={\frac {D_{E}/(D_{E}+H_{E})}{D_{N}/(D_{N}+H_{N})}}={\frac {D_{E}/V_{E}}{D_{N}/V_{N}}}={\frac {20/400}{6/600}}={\frac {.05}{.01}}=5\,.}$

Отношение шансов разное. Шансы заболеть, если подвергся воздействию, равны , а шансы, если не подвергся воздействию, равны. Отношение шансов — это отношение двух, ${\displaystyle D_{E}/H_{E}=20/380\approx .0526,}$ ${\displaystyle D_{N}/H_{N}=6/594\approx .0101\,.}$

${\displaystyle {\text{Odds ratio}}={\frac {D_{E}/H_{E}}{D_{N}/H_{N}}}={\frac {20/380}{6/594}}\approx {\frac {.0526}{.0101}}=5.2\,.}$

Как показано на этом примере, в случае редкого заболевания, как этот, относительный риск и отношение шансов почти одинаковы. По определению, редкое заболевание подразумевает, что и . Таким образом, знаменатели относительного риска и отношения шансов почти одинаковы ( и . ${\displaystyle V_{E}\approx H_{E}}$ ${\displaystyle V_{N}\approx H_{N}}$ ${\displaystyle 400\approx 380}$ ${\displaystyle 600\approx 594)}$

Относительный риск легче понять, чем отношение шансов, но одна из причин использования отношения шансов заключается в том, что обычно данные по всему населению недоступны, и необходимо использовать случайную выборку . В приведенном выше примере, если бы было очень дорого опросить жителей деревни и выяснить, подвергались ли они воздействию радиации, то распространенность воздействия радиации не была бы известна, как и значения или . Можно было бы взять случайную выборку из пятидесяти жителей деревни, но вполне возможно, что такая случайная выборка не включала бы никого с заболеванием, поскольку только 2,6% населения больны. Вместо этого можно было бы использовать исследование случай-контроль ^[2], в котором опрашиваются все 26 больных жителей деревни, а также случайная выборка из 26 не больных. Результаты могут оказаться следующими («могут», потому что это случайная выборка): ${\displaystyle V_{E}}$ ${\displaystyle V_{N}}$

${\displaystyle {\begin{array}{|r|cc|}\hline &{\text{ Diseased }}&{\text{ Healthy }}\\\hline {\text{ Exposed }}&20&10\\{\text{ Not exposed }}&6&16\\\hline \end{array}}}$

Вероятность заболеть в этой выборке при условии, что кто-то подвергнется воздействию, составляет 20/10, а вероятность, что кто-то не подвергнется воздействию, составляет 6/16. Таким образом , отношение шансов составляет , что довольно близко к отношению шансов, рассчитанному для всей деревни. Однако относительный риск не может быть рассчитан, поскольку это отношение рисков заболеть, и нам понадобятся и , чтобы их вычислить. Поскольку исследование было выбрано для людей с заболеванием, половина людей в выборке имеют это заболевание, и известно, что это больше, чем распространенность в популяции. ${\displaystyle {\frac {20/10}{6/16}}\approx 5.3}$ ${\displaystyle V_{E}}$ ${\displaystyle V_{N}}$

В медицинской литературе принято рассчитывать отношение шансов, а затем использовать предположение о редком заболевании (которое обычно разумно) для утверждения, что относительный риск приблизительно равен ему. Это не только позволяет использовать исследования случай-контроль, но и упрощает контроль за сопутствующими переменными, такими как вес или возраст, с помощью регрессионного анализа и обладает желательными свойствами, обсуждаемыми в других разделах этой статьи, инвариантностью и нечувствительностью к типу выборки. ^[3]

Определение с точки зрения групповых шансов

Отношение шансов — это отношение шансов события , происходящего в одной группе, к шансам его возникновения в другой группе. Этот термин также используется для обозначения выборочных оценок этого отношения. Эти группы могут быть мужчинами и женщинами, экспериментальной группой и контрольной группой или любой другой дихотомической классификацией. Если вероятности события в каждой из групп равны p ₁ (первая группа) и p ₂ (вторая группа), то отношение шансов равно:

${\displaystyle OR={\frac {p_{1}/(1-p_{1})}{p_{2}/(1-p_{2})}}={\frac {p_{1}/q_{1}}{p_{2}/q_{2}}}={\frac {\;p_{1}q_{2}\;}{\;p_{2}q_{1}\;}},}$

где q _x  = 1 −  p _x . Отношение шансов 1 указывает на то, что изучаемое состояние или событие с одинаковой вероятностью возникнет в обеих группах. Отношение шансов больше 1 указывает на то, что состояние или событие с большей вероятностью возникнет в первой группе. А отношение шансов меньше 1 указывает на то, что состояние или событие с меньшей вероятностью возникнет в первой группе. Отношение шансов должно быть неотрицательным, если оно определено. Оно не определено, если p ₂ q ₁ равно нулю, т. е. если p ₂ равно нулю или q ₁ равно нулю.

Определение в терминах совместных и условных вероятностей

Отношение шансов также можно определить в терминах совместного распределения вероятностей двух бинарных случайных величин . Совместное распределение бинарных случайных величин X и Y можно записать

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&p_{11}&p_{10}\\X=0&p_{01}&p_{00}\end{array}}}$

где p ₁₁ , p ₁₀ , p ₀₁ и p ₀₀ являются неотрицательными "вероятностями ячеек", которые в сумме дают единицу. Шансы для Y в двух субпопуляциях, определяемых X = 1 и X = 0, определяются в терминах условных вероятностей , заданных X , т.е. P ( Y  | X ) :

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&{\frac {p_{11}}{p_{11}+p_{10}}}&{\frac {p_{10}}{p_{11}+p_{10}}}\\X=0&{\frac {p_{01}}{p_{01}+p_{00}}}&{\frac {p_{00}}{p_{01}+p_{00}}}\end{array}}}$

Таким образом, отношение шансов равно

${\displaystyle OR={\dfrac {p_{11}/(p_{11}+p_{10})}{p_{10}/(p_{11}+p_{10})}}{\bigg /}{\dfrac {p_{01}/(p_{01}+p_{00})}{p_{00}/(p_{01}+p_{00})}}={\frac {p_{11}p_{00}}{p_{10}p_{01}}}}$

Простое выражение справа, выше, легко запомнить как произведение вероятностей "согласованных ячеек" ( X  =  Y ), деленное на произведение вероятностей "дискордантных ячеек" ( X  ≠  Y ) . Однако в некоторых приложениях маркировка категорий как ноль и единица произвольна, поэтому нет ничего особенного в согласованных и дискордантных значениях в этих приложениях.

Симметрия

Если бы мы рассчитали отношение шансов на основе условных вероятностей, заданных Y ,

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&{\frac {p_{11}}{p_{11}+p_{01}}}&{\frac {p_{10}}{p_{10}+p_{00}}}\\X=0&{\frac {p_{01}}{p_{11}+p_{01}}}&{\frac {p_{00}}{p_{10}+p_{00}}}\end{array}}}$

мы бы получили тот же результат

${\displaystyle {\dfrac {p_{11}/(p_{11}+p_{01})}{p_{01}/(p_{11}+p_{01})}}{\bigg /}{\dfrac {p_{10}/(p_{10}+p_{00})}{p_{00}/(p_{10}+p_{00})}}={\dfrac {p_{11}p_{00}}{p_{10}p_{01}}}.}$

Другие меры размера эффекта для двоичных данных , такие как относительный риск, не обладают этим свойством симметрии.

Отношение к статистической независимости

Если X и Y независимы, их совместные вероятности можно выразить через их предельные вероятности p _x  =  P ( X  = 1) и p _y  =  P ( Y  = 1) следующим образом:

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&p_{x}p_{y}&p_{x}(1-p_{y})\\X=0&(1-p_{x})p_{y}&(1-p_{x})(1-p_{y})\end{array}}}$

В этом случае отношение шансов равно единице, и наоборот, отношение шансов может быть равно единице только в том случае, если совместные вероятности могут быть разложены таким образом. Таким образом, отношение шансов равно единице тогда и только тогда, когда X и Y независимы .

Восстановление вероятностей ячеек из отношения шансов и предельных вероятностей

Отношение шансов является функцией вероятностей ячеек, и наоборот, вероятности ячеек могут быть восстановлены, зная отношение шансов и предельные вероятности P ( X  = 1) =  p ₁₁  +  p ₁₀ и P ( Y  = 1) =  p ₁₁  +  p _01. Если отношение шансов R отличается от 1, то

${\displaystyle p_{11}={\frac {1+(p_{1\cdot }+p_{\cdot 1})(R-1)-S}{2(R-1)}}}$

где p _1•  =  p ₁₁  +  p ₁₀ ,   p _•1  =  p ₁₁  +  p ₀₁ , и

${\displaystyle S={\sqrt {(1+(p_{1\cdot }+p_{\cdot 1})(R-1))^{2}+4R(1-R)p_{1\cdot }p_{\cdot 1}}}.}$

В случае, когда R  = 1 , мы имеем независимость, поэтому p ₁₁  =  p _1• p _•1 .

Как только у нас будет p ₁₁ , вероятности остальных трех ячеек можно легко восстановить из предельных вероятностей.

Пример

График, показывающий, как логарифм отношения шансов соотносится с базовыми вероятностями исхода X, происходящего в двух группах, обозначенных A и B. Логарифм отношения шансов, показанный здесь, основан на шансах события, происходящего в группе B, относительно шансов события, происходящего в группе A. Таким образом, когда вероятность того, что X произойдет в группе B , больше вероятности того, что X произойдет в группе A , отношение шансов больше 1, а логарифм отношения шансов больше 0.

Предположим, что в выборке из 100 мужчин 90 пили вино на предыдущей неделе (то есть 10 не пили), а в выборке из 80 женщин только 20 пили вино за тот же период (то есть 60 не пили). Это формирует таблицу сопряженности:

${\displaystyle {\begin{array}{c|cc}&M=1&M=0\\\hline D=1&90&20\\D=0&10&60\end{array}}}$

Отношение шансов (OR) можно рассчитать напрямую из этой таблицы следующим образом:

${\displaystyle {OR}={\frac {\;90\times 60\;}{\;10\times 20\;}}=27}$

В качестве альтернативы, шансы мужчины, пьющего вино, составляют 90 к 10, или 9:1, в то время как шансы женщины, пьющей вино, составляют всего 20 к 60, или 1:3 = 0,33. Таким образом, отношение шансов составляет 9/0,33, или 27, показывая, что мужчины гораздо более склонны пить вино, чем женщины. Подробный расчет:

${\displaystyle {0.9/0.1 \over 0.2/0.6}={\frac {\;0.9\times 0.6\;}{\;0.1\times 0.2\;}}={0.54 \over 0.02}=27}$

Этот пример также показывает, как отношения шансов иногда чувствительны при указании относительных позиций: в этой выборке мужчины в (90/100)/(20/80) = 3,6 раза чаще пили вино, чем женщины, но имеют в 27 раз больше шансов. Логарифм отношения шансов, разность логитов вероятностей , смягчает этот эффект, а также делает меру симметричной относительно порядка групп. Например, при использовании натуральных логарифмов отношение шансов 27/1 отображается в 3,296, а отношение шансов 1/27 отображается в −3,296.

Статистический вывод

График, показывающий минимальное значение статистики отношения шансов выборки, которое должно соблюдаться, чтобы считаться значимым на уровне 0,05, для данного размера выборки. Три линии соответствуют различным настройкам предельных вероятностей в таблице сопряженности 2×2 (предельные вероятности строк и столбцов на этом графике равны).

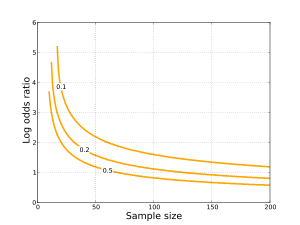
Было разработано несколько подходов к статистическому выводу для отношения шансов.

Один из подходов к выводу использует приближения выборки больших выборок к распределению выборки логарифма отношения шансов ( натуральный логарифм отношения шансов). Если мы используем обозначение совместной вероятности, определенное выше, то логарифм отношения шансов популяции равен

${\displaystyle {\log \left({\frac {p_{11}p_{00}}{p_{01}p_{10}}}\right)=\log(p_{11})+\log(p_{00}{\big )}-\log(p_{10})-\log(p_{01})}.\,}$

Если мы рассмотрим данные в виде таблицы сопряженности

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&n_{11}&n_{10}\\X=0&n_{01}&n_{00}\end{array}}}$

тогда вероятности в совместном распределении можно оценить как

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&{\hat {p}}_{11}&{\hat {p}}_{10}\\X=0&{\hat {p}}_{01}&{\hat {p}}_{00}\end{array}}}$

где︿п_ij  =  n _ij  /  n , где n  =  n ₁₁  +  n ₁₀  +  n ₀₁  +  n ₀₀ — сумма всех четырех подсчетов клеток. Отношение шансов логарифма выборки равно

${\displaystyle {L=\log \left({\dfrac {{\hat {p}}_{11}{\hat {p}}_{00}}{{\hat {p}}_{10}{\hat {p}}_{01}}}\right)=\log \left({\dfrac {n_{11}n_{00}}{n_{10}n_{01}}}\right)}}$.

Распределение логарифма отношения шансов приблизительно нормальное :

${\displaystyle L\ \sim \ {\mathcal {N}}(\log(OR),\,\sigma ^{2}).\,}$

Стандартная ошибка для логарифмического отношения шансов составляет приблизительно

${\displaystyle {{\rm {SE}}={\sqrt {{\dfrac {1}{n_{11}}}+{\dfrac {1}{n_{10}}}+{\dfrac {1}{n_{01}}}+{\dfrac {1}{n_{00}}}}}}}$.

Это асимптотическое приближение, и оно не даст осмысленного результата, если количество клеток очень мало. Если L — это отношение шансов логарифма выборки, приблизительный 95% доверительный интервал для отношения шансов логарифма популяции составляет L  ± 1,96SE . ^[4] Это можно отобразить в exp( L  − 1,96SE), exp( L  + 1,96SE), чтобы получить 95% доверительный интервал для отношения шансов. Если мы хотим проверить гипотезу о том, что отношение шансов популяции равно единице, двустороннее p-значение равно 2 P ( Z  < −| L |/SE) , где P обозначает вероятность, а Z обозначает стандартную нормальную случайную величину .

Альтернативный подход к выводу для отношения шансов рассматривает распределение данных условно на предельных частотах X и Y. Преимущество этого подхода заключается в том, что выборочное распределение отношения шансов может быть выражено точно.

Роль в логистической регрессии

Логистическая регрессия — один из способов обобщения отношения шансов за пределы двух бинарных переменных. Предположим, у нас есть бинарная переменная отклика Y и бинарная предикторная переменная X , и в дополнение к этому у нас есть другие предикторные переменные Z ₁ , ..., Z _{p ,} которые могут быть или не быть бинарными. Если мы используем множественную логистическую регрессию для регрессии Y на X , Z ₁ , ..., Z _p , то оценочный коэффициент для X связан с условным отношением шансов. В частности, на уровне популяции ${\displaystyle {\hat {\beta }}_{x}}$

${\displaystyle e^{\beta _{x}}=\exp(\beta _{x})={\frac {P(Y=1\mid X=1,Z_{1},\ldots ,Z_{p})/P(Y=0\mid X=1,Z_{1},\ldots ,Z_{p})}{P(Y=1\mid X=0,Z_{1},\ldots ,Z_{p})/P(Y=0\mid X=0,Z_{1},\ldots ,Z_{p})}},}$

так же является оценкой этого условного отношения шансов. Интерпретация заключается в оценке отношения шансов между Y и X, когда значения Z ₁ , ..., Z _p удерживаются фиксированными. ${\displaystyle \exp({\hat {\beta }}_{x})}$ ${\displaystyle \exp({\hat {\beta }}_{x})}$

Нечувствительность к типу выборки

Если данные формируют «выборку популяции», то вероятности ячеек интерпретируются как частоты каждой из четырех групп в популяции, определяемые их значениями X и Y. Во многих случаях получение выборки популяции нецелесообразно, поэтому используется выбранная выборка. Например, мы можем выбрать выборку единиц с X  = 1 с заданной вероятностью f , независимо от их частоты в популяции (что потребует выборки единиц с X  = 0 с вероятностью 1 −  f ). В этой ситуации наши данные будут следовать следующим совместным вероятностям: ${\displaystyle {\widehat {p\,}}_{ij}}$

${\displaystyle {\begin{array}{c|cc}&Y=1&Y=0\\\hline X=1&{\frac {fp_{11}}{p_{11}+p_{10}}}&{\frac {fp_{10}}{p_{11}+p_{10}}}\\X=0&{\frac {(1-f)p_{01}}{p_{01}+p_{00}}}&{\frac {(1-f)p_{00}}{p_{01}+p_{00}}}\end{array}}}$

Отношение шансов p ₁₁ p ₀₀  /  p ₀₁ p ₁₀ для этого распределения не зависит от значения f . Это показывает, что отношение шансов (и, следовательно, логарифм отношения шансов) инвариантно к неслучайной выборке, основанной на одной из изучаемых переменных. Однако следует отметить, что стандартная ошибка логарифма отношения шансов зависит от значения f . ^{[ необходима цитата ]}

Этот факт используется в двух важных ситуациях:

• Предположим, что получение выборки населения неудобно или нецелесообразно, но практично получить удобную выборку единиц с разными значениями X , так что в подвыборках X  = 0 и X  = 1 значения Y являются репрезентативными для населения (т.е. они следуют правильным условным вероятностям).
• Предположим, что предельное распределение одной переменной, скажем, X , очень неравномерно. Например, если мы изучаем связь между высоким потреблением алкоголя и раком поджелудочной железы в общей популяции, заболеваемость раком поджелудочной железы будет очень низкой, поэтому потребуется очень большая выборка населения, чтобы получить скромное количество случаев рака поджелудочной железы. Однако мы могли бы использовать данные из больниц, чтобы связаться с большинством или всеми их пациентами с раком поджелудочной железы, а затем случайным образом выбрать равное количество субъектов без рака поджелудочной железы (это называется «исследование случай-контроль»).

В обоих случаях отношение шансов можно рассчитать на основе выбранной выборки, не искажая результаты по сравнению с тем, что было бы получено для выборки населения.

Использование в количественных исследованиях

Из-за широкого использования логистической регрессии отношение шансов широко используется во многих областях медицинских и социальных исследований. Отношение шансов обычно используется в исследованиях опросов , в эпидемиологии и для выражения результатов некоторых клинических испытаний , таких как исследования случай-контроль . В отчетах его часто сокращают до «OR». Когда данные из нескольких опросов объединяются, они часто будут выражаться как «объединенный OR».

Отношение к относительному риску

Соотношение риска и отношение шансов

Как объясняется в разделе «Мотивирующий пример», относительный риск обычно лучше, чем отношение шансов, для понимания связи между риском и некоторой переменной, такой как радиация или новый препарат. В этом разделе также объясняется, что если предположение о редком заболевании выполняется, отношение шансов является хорошим приближением к относительному риску ^[5] и что оно имеет некоторые преимущества по сравнению с относительным риском. Когда предположение о редком заболевании не выполняется, нескорректированное отношение шансов будет больше относительного риска, ^{[6] [7] [8]} но новые методы могут легко использовать те же данные для оценки относительного риска, различий в рисках, базовых вероятностей или других величин. ^[9]

Если абсолютный риск в группе, не подвергшейся воздействию, известен, то преобразование между ними рассчитывается по формуле: ^[6]

${\displaystyle {\text{Relative risk}}\approx {\frac {\text{Odds ratio}}{1-R_{C}+(R_{C}\times {\text{Odds ratio}})}}}$

где R _C — абсолютный риск для группы, не подвергшейся воздействию.

Если предположение о редкости заболевания не применимо, отношение шансов может сильно отличаться от относительного риска и не должно интерпретироваться как относительный риск.

Рассмотрим уровень смертности мужчин и женщин-пассажиров, когда затонуло судно. ^[3] Из 462 женщин 154 погибли, а 308 выжили. Из 851 мужчины 709 погибли, а 142 выжили. Очевидно, что мужчина на судне имел больше шансов умереть, чем женщина, но насколько больше? Поскольку более половины пассажиров погибли, предположение о редком заболевании сильно нарушается.

Чтобы вычислить отношение шансов, обратите внимание, что для женщин шансы умереть были 1 к 2 (154/308). Для мужчин шансы были 5 к 1 (709/142). Отношение шансов составляет 9,99 (4,99/.5). У мужчин шансы умереть были в десять раз выше, чем у женщин.

Для женщин вероятность смерти составила 33% (154/462). Для мужчин вероятность составила 83% (709/851). Относительный риск смерти составил 2,5 (.83/.33). Вероятность смерти у мужчины была в 2,5 раза выше, чем у женщины.

Путаница и преувеличение

В медицинской литературе коэффициенты шансов часто путают с относительным риском. Для нестатистиков коэффициент шансов — это сложная для понимания концепция, и она дает более впечатляющую цифру для эффекта. ^[10] Однако большинство авторов считают, что относительный риск легко понять. ^[11] В одном исследовании члены национального фонда заболеваний на самом деле в 3,5 раза чаще, чем не члены, слышали о распространенном лечении этого заболевания — но коэффициент шансов был 24, и в статье говорилось, что члены «более чем в 20 раз чаще слышали» о лечении. ^[12] Исследование статей, опубликованных в двух журналах, показало, что 26% статей, в которых использовалось отношение шансов, интерпретировали его как отношение риска. ^[13]

Это может отражать простой процесс выбора авторами, не понимающими сути, наиболее впечатляющей и пригодной для публикации цифры. ^[11] Но в некоторых случаях ее использование может быть намеренно обманчивым. ^[14] Было высказано предположение, что отношение шансов должно быть представлено как мера размера эффекта только тогда, когда отношение риска не может быть оценено напрямую, ^[10] но с помощью новых доступных методов всегда можно оценить отношение риска, которое, как правило, следует использовать вместо этого. ^[9]

Хотя относительные риски потенциально легче интерпретировать для широкой аудитории, существуют математические и концептуальные преимущества при использовании отношения шансов вместо относительного риска, особенно в регрессионных моделях. По этой причине в областях эпидемиологии или биостатистики нет консенсуса о том, что относительные риски или отношения шансов должны быть предпочтительными, когда оба могут быть обоснованно использованы, например, в клинических испытаниях и когортных исследованиях ^[15]

Обратимость и инвариантность

Отношение шансов имеет еще одно уникальное свойство: оно напрямую математически обратимо, независимо от того, анализируется ли OR как выживаемость при заболевании или заболеваемость с началом заболевания – где OR для выживания является прямой обратной величиной 1/OR для риска. Это известно как «инвариантность отношения шансов». Напротив, относительный риск не обладает этим математически обратимым свойством при изучении выживаемости при заболевании в сравнении с заболеваемостью с началом заболевания. Этот феномен обратимости OR против необратимости RR лучше всего проиллюстрировать на примере:

Предположим, что в клиническом испытании риск неблагоприятного события составляет 4/100 в группе, принимающей лекарство, и 2/100 в группе, принимающей плацебо... что дает RR=2 и OR=2,04166 для неблагоприятного риска «лекарство против плацебо». Однако, если бы анализ был инвертирован и неблагоприятные события были бы проанализированы как выживаемость без событий, то группа, принимающая лекарство, имела бы показатель 96/100, а группа, принимающая плацебо, имела бы показатель 98/100, что дало бы «лекарство против плацебо» RR=0,9796 для выживания, но OR=0,48979. Как можно видеть, RR 0,9796 явно не является обратной величиной RR 2. Напротив, OR 0,48979 действительно является прямой обратной величиной OR 2,04166.

Это снова то, что называется «инвариантностью отношения шансов», и почему RR для выживания не то же самое, что RR для риска, в то время как OR имеет это симметричное свойство при анализе как выживания, так и неблагоприятного риска. Опасность для клинической интерпретации OR возникает, когда частота неблагоприятных событий не является редкой, тем самым преувеличивая различия, когда предположение OR о редком заболевании не выполняется. С другой стороны, когда заболевание редкое, использование RR для выживания (например, RR=0,9796 из приведенного выше примера) может клинически скрыть и замаскировать важное удвоение неблагоприятного риска, связанного с препаратом или воздействием. ^{[ необходима цитата ]}

Оценщики отношения шансов

Отношение шансов выборки

Отношение шансов выборки n ₁₁ n ₀₀  /  n ₁₀ n ₀₁ легко вычисляется, и для умеренных и больших выборок хорошо подходит в качестве оценщика отношения шансов популяции. Когда одна или несколько ячеек в таблице сопряженности могут иметь небольшое значение, отношение шансов выборки может быть смещено и демонстрировать высокую дисперсию .

Альтернативные оценщики

Для устранения ограничений выборочного отношения шансов было предложено несколько альтернативных оценок отношения шансов. Одной из альтернативных оценок является оценка условного максимального правдоподобия, которая учитывает поля строк и столбцов при формировании вероятности для максимизации (как в точном тесте Фишера ). ^[16] Другой альтернативной оценкой является оценка Мантеля–Хензеля . ^{[ требуется ссылка ]}

Числовые примеры

Следующие четыре таблицы сопряженности содержат наблюдаемые количества клеток, а также соответствующее отношение шансов выборки ( OR ) и отношение шансов логарифма выборки ( LOR ):

Следующие совместные распределения вероятностей содержат вероятности ячеек популяции, а также соответствующее отношение шансов популяции ( OR ) и логарифмическое отношение шансов популяции ( LOR ):

Числовой пример

Сопутствующая статистика

Существуют различные другие сводные статистики для таблиц сопряженности , которые измеряют связь между двумя событиями, такими как Y Юла , Q Юла ; эти две величины нормализованы, поэтому они равны 0 для независимых событий, 1 для идеально коррелированных, −1 для идеально отрицательно коррелированных. Эдвардс (1963) изучал их и утверждал, что эти меры ассоциации должны быть функциями отношения шансов, которое он называл перекрестным отношением . [ ^{необходима цитата ]}

Отношение шансов для сопоставленного исследования случай-контроль

Исследование случай-контроль включает в себя выборку репрезентативных выборок случаев и контрольных групп, которые имеют и не имеют некоторые заболевания соответственно. Эти выборки обычно независимы друг от друга. Предшествующая распространенность воздействия некоторого фактора риска наблюдается у субъектов из обеих выборок. Это позволяет оценить отношение шансов для заболевания у подвергшихся воздействию и не подвергшихся воздействию людей, как отмечено выше. ^[17] Однако иногда имеет смысл сопоставлять случаи с контрольными группами по одной или нескольким смешивающим переменным. ^[18] В этом случае предшествующее воздействие, представляющее интерес, определяется для каждого случая и его/ее соответствующего контроля. Данные можно обобщить в следующей таблице.

Таблица 2x2

В этой таблице указан статус воздействия сопоставленных пар субъектов. Есть пары, где и случай, и его сопоставленный контроль были подвергнуты воздействию, пары, где пациент-случай был подвергнут воздействию, а контрольный субъект — нет, пары, где контрольный субъект подвергся воздействию, а пациент-случай — нет, и пары, где ни один из субъектов не подвергся воздействию. Воздействие сопоставленных пар случай и контроль коррелирует из-за схожих значений их общих смешивающих переменных. ${\displaystyle n_{11}}$ ${\displaystyle n_{10}}$ ${\displaystyle n_{01}}$ ${\displaystyle n_{00}}$

Следующий вывод принадлежит Бреслоу и Дей . ^[18] Мы рассматриваем каждую пару как принадлежащую к страте с идентичными значениями смешивающих переменных. При условии принадлежности к одной и той же страте статус экспозиции случаев и контролей независим друг от друга. Для любой пары случай-контроль в пределах одной и той же страты пусть

${\displaystyle p_{1}}$быть вероятностью того, что пациент подвергнется заражению,

${\displaystyle p_{0}}$быть вероятностью того, что контрольный пациент подвергнется воздействию,

${\displaystyle q_{1}=1-p_{1}}$быть вероятностью того, что пациент не подвергнется воздействию, и

${\displaystyle q_{0}=1-p_{0}}$вероятность того, что контрольный пациент не подвергнется воздействию.

Тогда вероятность того, что случай подвергается воздействию, а контроль — нет, равна , а вероятность того, что контроль подвергается воздействию, а случай — нет, равна . Внутристратовое отношение шансов для воздействия в случаях относительно контроля равно ${\displaystyle p_{1}q_{0}}$ ${\displaystyle p_{0}q_{1}}$

${\displaystyle \psi =(p_{1}/q_{1})/(p_{0}/q_{0})=p_{1}q_{0}/(q_{1}p_{0})}$

Мы предполагаем, что это постоянно во всех слоях. ^[18] ${\displaystyle \psi }$

Теперь согласованные пары, в которых либо оба случая и контроль подвергаются воздействию, либо ни один из них не подвергается воздействию, ничего не говорят нам о шансах воздействия в случаях относительно шансов воздействия среди контролей. Вероятность того, что случай подвергается воздействию, а контроль не подвергается воздействию, учитывая, что пара является несогласованной, равна

${\displaystyle \pi =(p_{1}q_{0})/(p_{1}q_{0}+q_{1}p_{0})=\psi /(\psi +1)}$

Распределение с учетом числа несогласованных пар является биномиальным  ~ B , а оценка максимального правдоподобия равна ${\displaystyle n_{10}}$ ${\displaystyle (n_{10}+n_{01},\pi )}$ ${\displaystyle \pi }$

${\displaystyle {\hat {\pi }}=n_{10}/(n_{10}+n_{01})={\hat {\psi }}/({\hat {\psi }}+1)}$

Умножение обеих частей этого уравнения на и вычитание дает ${\displaystyle (n_{10}+n_{01})({\hat {\psi }}+1)}$ ${\displaystyle n_{10}{\hat {\psi }}}$

${\displaystyle n_{10}={\hat {\psi }}(n_{10}+n_{01}-n_{10})}$и, следовательно,

${\displaystyle {\hat {\psi }}=n_{10}/n_{01}}$.

Теперь — оценка максимального правдоподобия , и — монотонная функция . Отсюда следует, что — условная оценка максимального правдоподобия для данного числа несогласованных пар. Ротман и др. ^[19] приводят альтернативный вывод, показывая, что это особый случай оценки Мантеля-Хензеля внутристратового отношения шансов для стратифицированных таблиц 2x2. ^[19] Они также ссылаются на Бреслоу и Дэя ^[18] как на лиц, предоставивших приведенный здесь вывод. ${\displaystyle {\hat {\pi }}}$ ${\displaystyle \pi }$ ${\displaystyle \psi }$ ${\displaystyle {\hat {\pi }}}$ ${\displaystyle {\hat {\psi }}}$ ${\displaystyle {\hat {\psi }}}$ ${\displaystyle {\hat {\psi }}}$

При нулевой гипотезе, что . ${\displaystyle \psi =1,\pi =1/(1+1)=0.5}$

Следовательно, мы можем проверить нулевую гипотезу, проверив нулевую гипотезу, что . Это делается с помощью теста Макнемара . ${\displaystyle \psi =1}$ ${\displaystyle \pi =0.5}$

Существует несколько способов вычисления доверительного интервала для . Пусть и обозначают нижнюю и верхнюю границу доверительного интервала для , соответственно. Поскольку , соответствующий доверительный интервал для равен ${\displaystyle \pi }$ ${\displaystyle {\hat {\pi }}_{LB}}$ ${\displaystyle {\hat {\pi }}_{UB}}$ ${\displaystyle \pi }$ ${\displaystyle \psi =\pi /(1-\pi )}$ ${\displaystyle \psi }$

${\displaystyle ({\frac {{\hat {\pi }}_{LB}}{1-{\hat {\pi }}_{LB}}},{\frac {{\hat {\pi }}_{UB}}{1-{\hat {\pi }}_{UB}}})}$.

Сопоставленные таблицы 2x2 также можно анализировать с помощью условной логистической регрессии . ^[20] Этот метод имеет преимущество, поскольку позволяет пользователям регрессировать статус случай-контроль по отношению к нескольким факторам риска из сопоставленных данных случай-контроль.

Пример

МакЭвой и др. ^[21] изучали использование сотовых телефонов водителями как фактор риска автомобильных аварий в перекрестном исследовании случаев. ^[17] Все субъекты исследования были вовлечены в автомобильную аварию, потребовавшую госпитализации. Использование сотового телефона каждым водителем во время его/ее аварии сравнивалось с использованием его/ее сотового телефона в контрольный интервал в то же время дня неделей ранее. Мы ожидаем, что использование сотового телефона человеком во время аварии будет коррелировать с его/ее использованием неделей ранее. Сравнение использования во время аварии и контрольных интервалов корректирует характеристики водителя, а также время дня и день недели. Данные можно обобщить в следующей таблице.

5 водителей использовали свои телефоны в обоих интервалах, 27 использовали их в аварии, но не в контрольном интервале, 6 использовали их в контрольном интервале, но не в аварийном, и 288 не использовали их ни в одном из интервалов. Отношение шансов для аварии с использованием телефона по сравнению с вождением без использования телефона было

${\displaystyle {\hat {\psi }}=27/6=4.5}$.

Проверка нулевой гипотезы, которая совпадает с проверкой нулевой гипотезы, которая дает 27 из 33 несогласованных пар, в которых водитель использовал свой телефон во время аварии. Макнемара . Эта статистика имеет одну степень свободы и дает значение P 0,0003. Это позволяет нам отвергнуть гипотезу о том, что использование мобильного телефона не влияет на риск автомобильных аварий ( ) с высоким уровнем статистической значимости. ${\displaystyle {\hat {\psi }}=1}$ ${\displaystyle {\hat {\pi }}=0.5}$ ${\displaystyle \chi ^{2}=13.36}$ ${\displaystyle \psi =1}$

Используя метод Уилсона , 95% доверительный интервал для равен (0,6561, 0,9139). Следовательно, 95% доверительный интервал для равен ${\displaystyle \pi }$ ${\displaystyle \psi }$

${\displaystyle ({\frac {0.6561}{1-0.6561}},{\frac {0.9139}{1-0.9139}})=(1.9,10.6)}$

(МакЭвой и др. ^[21] проанализировали свои данные с помощью условной логистической регрессии и получили почти идентичные результаты, приведенные здесь. См. последнюю строку таблицы 3 в их статье.)

Смотрите также

• Коэн h
• Кросс-соотношение
• Диагностическое отношение шансов
• Лесной участок
• Коэффициент опасности
• Коэффициент правдоподобия
• Коэффициент ставки

Ссылки

Цитаты

1. Szumilas M (август 2010 г.). «Объяснение отношения шансов». Журнал Канадской академии детской и подростковой психиатрии . 19 (3): 227–229. ISSN  1719-8429. PMC 2938757.  PMID 20842279  .
2. LaMorte WW (13 мая 2013 г.), Исследования случай-контроль, Бостонский университет, Школа общественного здравоохранения , архивировано из оригинала 2013-10-08 , извлечено 2013-09-02
3. Simon S (июль–август 2001 г.). «Понимание отношения шансов и относительного риска». Журнал андрологии . 22 (4): 533–536. doi : 10.1002/j.1939-4640.2001.tb02212.x . PMID  11451349. S2CID  6150799.
4. Morris JA, Gardner MJ (май 1988). «Вычисление доверительных интервалов для относительных рисков (коэффициентов шансов) и стандартизированных коэффициентов и показателей». British Medical Journal (Clinical Research Ed.) . 296 (6632): 1313–6. doi :10.1136/bmj.296.6632.1313. PMC 2545775. PMID  3133061 . 
5. Viera AJ (июль 2008 г.). «Отношения шансов и отношения рисков: в чем разница и почему это важно?». Southern Medical Journal . 101 (7): 730–4. doi :10.1097/SMJ.0b013e31817a7ee4. PMID  18580722.
6. Zhang J, Yu KF (ноябрь 1998 г.). «Каков относительный риск? Метод коррекции отношения шансов в когортных исследованиях общих результатов». JAMA . 280 (19): 1690–1. doi :10.1001/jama.280.19.1690. PMID  9832001. S2CID  30509187.
7. Robbins AS, Chao SY, Fonseca VP (октябрь 2002 г.). «Каков относительный риск? Метод прямой оценки коэффициентов риска в когортных исследованиях общих результатов». Annals of Epidemiology . 12 (7): 452–4. doi :10.1016/S1047-2797(01)00278-2. PMID  12377421.
8. Nurminen M (август 1995). «Использовать или не использовать отношение шансов в эпидемиологических анализах?». European Journal of Epidemiology . 11 (4): 365–71. doi :10.1007/BF01721219. PMID  8549701. S2CID  11609059.
9. King G, Zeng L (2002-05-30). "Оценка уровней риска и скорости, соотношений и различий в исследованиях случай-контроль" (PDF) . Статистика в медицине . 21 (10): 1409–1427. doi :10.1002/sim.1032. ISSN  0277-6715. PMID  12185893. S2CID  11387977.
10. Taeger D, Sun Y, Straif K (10 августа 1998 г.). «Об использовании, неправильном использовании и интерпретации отношений шансов».
11. A'Court C, Stevens R, Heneghan C (март 2012 г.). «Вопреки всем обстоятельствам? Улучшение понимания отчетности о рисках». Британский журнал общей практики . 62 (596): e220-3. doi :10.3399/bjgp12X630223. PMC 3289830. PMID  22429441 . 
12. Nijsten T, Rolstad T, Feldman SR, Stern RS (январь 2005 г.). «Члены национального фонда псориаза: более обширное заболевание и лучшая информированность о вариантах лечения». Архивы дерматологии . 141 (1): 19–26. doi :10.1001/archderm.141.1.19. PMID  15655138.
13. Холкомб В. (2001). «Странная мера риска: использование и неправильное использование отношения шансов». Акушерство и гинекология . 98 (4): 685–688. doi :10.1016/S0029-7844(01)01488-0. PMID  11576589. S2CID  44782438.
14. Taylor HG (январь 1975). «Социальное восприятие умственно отсталых». Журнал клинической психологии . 31 (1): 100–2. doi :10.1136/bmj.316.7136.989. PMC 1112884. PMID  9550961 . 
15. Комментарий к противоречиям и дебатам 4 серии статей: Сомнительная полезность относительного риска в клинических исследованиях. (2022/02//). Журнал клинической эпидемиологии, 142, 268-270. doi:https://doi.org/10.1016/j.jclinepi.2021.09.016
16. Ротман К. Дж., Гринланд С., Лэш Т. Л. (2008). Современная эпидемиология . Липпинкотт Уильямс и Уилкинс. ISBN 978-0-7817-5564-1.^{[ нужна страница ]}
17. Celentano DD, Szklo M, Gordis L (2019). Gordis Epidemiology, шестое издание . Филадельфия, Пенсильвания: Elsevier. стр. 149-177.
18. Бреслоу, NE, Дэй, NE (1980). Статистические методы в исследовании рака: Том 1 - Анализ исследований случай-контроль . Лион, Франция: Научные публикации IARC. стр. 162-189.
19. Rothman KJ, Greenland S, Lash TL (2008). Современная эпидемиология, третье издание . Филадельфия, Пенсильвания: Lippincott Williams & Wilkins. стр. 287,288.
20. Breslow NE, Day NE, Halvorsen KT, Prentice RL, Sabai C (1978). «Оценка множественных функций относительного риска в сопоставленных исследованиях случай-контроль». Am J Epidemiol . 108 (4): 299–307. doi :10.1093/oxfordjournals.aje.a112623. PMID  727199.
21. McEvoy SP, Stevenson MR, McCartt AT, Woodward M, Haworth C, Palamara P, Cercarelli R (2005). «Роль мобильных телефонов в дорожно-транспортных происшествиях, приводящих к госпитализации: перекрестное исследование случаев». BMJ . 331 (7514): 428. doi : 10.1136/bmj.38537.397512.55 . PMC 1188107 . PMID  16012176. 

Источники

• Эдвардс AW (1963). «Мера ассоциации в таблице 2 × 2». Журнал Королевского статистического общества . A (General). 126 (1): 109–114. doi :10.2307/2982448. JSTOR  2982448.

Внешние ссылки

• Калькулятор отношения шансов – веб-сайт
• Калькулятор отношения шансов с различными тестами – веб-сайт
• OpenEpi — веб-программа, которая вычисляет отношение шансов, как непарных, так и парных