Логистическая регрессия

Статистическая модель для бинарной зависимой переменной

Пример графика кривой логистической регрессии, адаптированной к данным. Кривая показывает предполагаемую вероятность сдачи экзамена (двоичная зависимая переменная) в зависимости от количества часов обучения (скалярная независимая переменная). Подробную информацию см. в § Примере.

В статистике логистическая модель (или логит-модель ) — это статистическая модель , которая моделирует логарифмические шансы события как линейную комбинацию одной или нескольких независимых переменных . В регрессионном анализе логистическая регрессия ^[1] (или логит-регрессия ) оценивает параметры логистической модели (коэффициенты в линейной комбинации). Формально в бинарной логистической регрессии существует одна двоичная зависимая переменная , кодируемая индикаторной переменной , где два значения помечены «0» и «1», в то время как каждая из независимых переменных может быть двоичной переменной (два класса, кодируемые индикаторная переменная) или непрерывная переменная (любое действительное значение). Соответствующая вероятность значения, помеченного «1», может варьироваться от 0 (определенно значения «0») до 1 (определенно значения «1»), отсюда и маркировка; ^[2] функция, которая преобразует логарифм шансов в вероятность, является логистической функцией , отсюда и название. Единица измерения шкалы логарифмических шансов называется логит , от слова логистическая единица , отсюда и альтернативные названия. См. § «История» и § «Определение» для формальной математики, а также § «Пример» для рабочего примера.

Бинарные переменные широко используются в статистике для моделирования вероятности возникновения определенного класса или события, например, вероятности победы команды, здоровья пациента и т. д. (см. § Приложения), а логистическая модель была наиболее часто используемая модель бинарной регрессии примерно с 1970 года. ^[3] Бинарные переменные можно обобщить до категориальных переменных , когда существует более двух возможных значений (например, изображение кошки, собаки, льва и т. д.), а бинарная логистическая регрессия, обобщенная до полиномиальной логистической регрессии . Если несколько категорий упорядочены , можно использовать порядковую логистическую регрессию (например, порядковую логистическую модель с пропорциональными шансами ^[4] ). Дополнительные расширения см. в § Расширения. Сама модель логистической регрессии просто моделирует вероятность выхода с точки зрения входных данных и не выполняет статистическую классификацию (это не классификатор), хотя ее можно использовать для создания классификатора, например, выбрав пороговое значение и классифицируя входные данные с вероятностью. больше порогового значения для одного класса и ниже порогового значения для другого; это распространенный способ создания двоичного классификатора .

Также могут использоваться аналогичные линейные модели для двоичных переменных с другой сигмовидной функцией вместо логистической функции (для преобразования линейной комбинации в вероятность), в первую очередь пробит-модель ; см. § Альтернативы. Определяющей характеристикой логистической модели является то, что увеличение одной из независимых переменных мультипликативно масштабирует шансы данного результата с постоянной скоростью, при этом каждая независимая переменная имеет свой собственный параметр; для двоичной зависимой переменной это обобщает отношение шансов . Говоря более абстрактно, логистическая функция является естественным параметром распределения Бернулли и в этом смысле является «простейшим» способом преобразования действительного числа в вероятность. В частности, он максимизирует энтропию (минимизирует добавленную информацию) и в этом смысле делает наименьшее количество предположений относительно моделируемых данных; см. § Максимальная энтропия.

Параметры логистической регрессии чаще всего оцениваются с помощью оценки максимального правдоподобия (MLE). В отличие от линейного метода наименьших квадратов , здесь нет выражения в замкнутой форме ; см. § Примерка модели. Логистическая регрессия с помощью MLE играет такую ​​же базовую роль для бинарных или категориальных ответов, как линейная регрессия с помощью обычных наименьших квадратов (OLS) играет для скалярных ответов: это простая, хорошо проанализированная базовая модель; см. § Сравнение с линейной регрессией для обсуждения. Логистическая регрессия как общая статистическая модель была первоначально разработана и популяризирована в первую очередь Джозефом Берксоном ^[5] , начиная с Берксона (1944), где он ввел термин «логит»; см. § История.

Приложения

Логистическая регрессия используется в различных областях, включая машинное обучение, большинство областей медицины и социальные науки. Например, шкала тяжести травм и травм ( TRISS ), которая широко используется для прогнозирования смертности пациентов с травмами, первоначально была разработана Boyd et al. с использованием логистической регрессии. ^[6] Многие другие медицинские шкалы, используемые для оценки тяжести состояния пациента, были разработаны с использованием логистической регрессии. ^{[7] [8] [9] [10]} Логистическую регрессию можно использовать для прогнозирования риска развития данного заболевания (например, диабета , ишемической болезни сердца ) на основе наблюдаемых характеристик пациента (возраст, пол, индекс массы тела). , результаты различных анализов крови и т. д.). ^{[11] [12]} Другим примером может быть прогнозирование того, проголосует ли непальский избиратель за Конгресс Непала, Коммунистическую партию Непала или любую другую партию, на основе возраста, дохода, пола, расы, штата проживания, голосов на предыдущих выборах и т. д. ^[13] Этот метод также можно использовать в технике , особенно для прогнозирования вероятности отказа данного процесса, системы или продукта . ^{[14] [15]} Он также используется в маркетинговых приложениях, таких как прогнозирование склонности клиента к покупке продукта или прекращению подписки и т. д. ^[16] В экономике его можно использовать для прогнозирования вероятности того, что человек в конечном итоге окажется в рабочей силе, а бизнес-приложение будет заключаться в прогнозировании вероятности того, что домовладелец не сможет выплатить ипотечный кредит . Условные случайные поля , расширение логистической регрессии на последовательные данные, используются при обработке естественного языка . Специалисты по планированию стихийных бедствий и инженеры полагаются на эти модели для прогнозирования решений, принимаемых домовладельцами или жильцами зданий при мелкомасштабной и крупномасштабной эвакуации, например, пожарах в зданиях, лесных пожарах, ураганах и других. ^{[17] [18] [19]} Эти модели помогают в разработке надежных планов борьбы со стихийными бедствиями и более безопасного проектирования искусственной среды .

Пример

Проблема

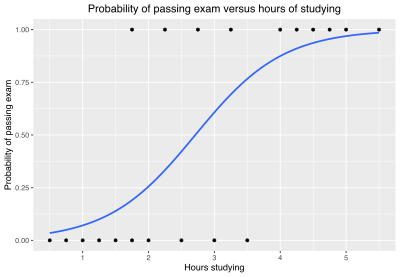
В качестве простого примера мы можем использовать логистическую регрессию с одной независимой переменной и двумя категориями, чтобы ответить на следующий вопрос:

Группа из 20 студентов тратит от 0 до 6 часов на подготовку к экзамену. Как количество часов, потраченных на обучение, влияет на вероятность сдачи студентом экзамена?

Причина использования логистической регрессии для этой задачи заключается в том, что значения зависимой переменной «пройдено» и «не пройдено», хотя и представлены «1» и «0», не являются кардинальными числами . Если бы проблема была изменена таким образом, что «прошел/не прошел» оценку от 0 до 100 (количественное число), то можно было бы использовать простой регрессионный анализ .

В таблице показано количество часов, потраченных на обучение каждым студентом, а также сведения о том, сдали ли они экзамен (1) или не сдали экзамен (0).

Мы хотим подогнать логистическую функцию к данным, состоящим из изученных часов ( x _k ) и результата теста ( y _k  =1 для прохождения, 0 для провала). Точки данных индексируются индексом k , который начинается с . Переменная x называется « объясняющей переменной », а переменная y называется « категорической переменной », состоящей из двух категорий: «пройден» или «не пройден», соответствующих категориальным значениям 1 и 0 соответственно. ${\displaystyle k=1}$ ${\displaystyle k=K=20}$

Модель

График кривой логистической регрессии, адаптированной к данным ( x _m , y _m ). Кривая показывает вероятность сдачи экзамена в зависимости от количества часов обучения.

Логистическая функция имеет вид:

${\displaystyle p(x)={\frac {1}{1+e^{-(x-\mu )/s}}}}$

где µ — параметр местоположения (середина кривой, где ), а s — параметр масштаба . Это выражение можно переписать так: ${\displaystyle p(\mu )=1/2}$

${\displaystyle p(x)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}}$

где и известен как точка пересечения (это вертикальная точка пересечения или точка пересечения по оси y линии ), и (параметр обратного масштаба или параметр скорости ): это точка пересечения по оси y и наклон логарифмических шансов как функция от x . И наоборот, и . ${\displaystyle \beta _{0}=-\mu /s}$ ${\displaystyle y=\beta _{0}+\beta _{1}x}$ ${\displaystyle \beta _{1}=1/s}$ ${\displaystyle \mu =-\beta _{0}/\beta _{1}}$ ${\displaystyle s=1/\beta _{1}}$

Соответствовать

Обычная мера согласия для логистической регрессии использует логистические потери (или логарифмические потери ), отрицательное логарифмическое правдоподобие . _Для заданных xk и yk напишите . _{_} Это вероятности того, что соответствующие значения будут равны единице, и вероятности того, что они будут равны нулю (см. Распределение Бернулли ). Мы хотим найти значения и которые наилучшим образом соответствуют данным. В случае линейной регрессии сумма квадратов отклонений аппроксимации от точек данных ( _yk ) , квадратичная потеря ошибки , принимается в качестве меры качества аппроксимации, и наилучшее аппроксимация получается, когда эта функция сведен к минимуму . ${\displaystyle p_{k}=p(x_{k})}$ ${\displaystyle p_{k}}$ ${\displaystyle y_{k}}$ ${\displaystyle 1-p_{k}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

Логарифмические потери для k -й точки составляют: ${\displaystyle \ell _{k}}$

${\displaystyle \ell _{k}={\begin{cases}-\ln p_{k}&{\text{ if }}y_{k}=1,\\-\ln(1-p_{k})&{\text{ if }}y_{k}=0.\end{cases}}}$

Потерю журнала можно интерпретировать как « сюрприз » фактического результата по сравнению с прогнозом , и он является мерой содержания информации . Логарифмические потери всегда больше или равны 0, равны 0 только в случае идеального прогноза (т. е. когда и , или и ) и приближаются к бесконечности по мере ухудшения прогноза (т. е. когда и или и ), что означает фактическое результат «более неожиданный». Поскольку значение логистической функции всегда находится строго между нулем и единицей, логарифмические потери всегда больше нуля и меньше бесконечности. В отличие от линейной регрессии, где модель может иметь нулевые потери в какой-либо точке при прохождении через точку данных (и нулевые потери в целом, если все точки находятся на линии), в логистической регрессии невозможно иметь нулевые потери в любой точке. баллов, так как либо 0, либо 1, но . ${\displaystyle y_{k}}$ ${\displaystyle p_{k}}$ ${\displaystyle p_{k}=1}$ ${\displaystyle y_{k}=1}$ ${\displaystyle p_{k}=0}$ ${\displaystyle y_{k}=0}$ ${\displaystyle y_{k}=1}$ ${\displaystyle p_{k}\to 0}$ ${\displaystyle y_{k}=0}$ ${\displaystyle p_{k}\to 1}$ ${\displaystyle y_{k}}$ ${\displaystyle 0<p_{k}<1}$

Их можно объединить в одно выражение:

${\displaystyle \ell _{k}=-y_{k}\ln p_{k}-(1-y_{k})\ln(1-p_{k}).}$

Это выражение более формально известно как кросс-энтропия предсказанного распределения от фактического распределения , как распределение вероятностей в двухэлементном пространстве (пройдено, не пройдено). ${\displaystyle {\big (}p_{k},(1-p_{k}){\big )}}$ ${\displaystyle {\big (}y_{k},(1-y_{k}){\big )}}$

Их сумма, общие потери, представляет собой общую отрицательную логарифмическую вероятность , и наилучшее соответствие получается для тех вариантов и для которых минимизировано . ${\displaystyle -\ell }$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$ ${\displaystyle -\ell }$

Альтернативно, вместо минимизации потерь можно максимизировать обратную величину (положительную) логарифмическую вероятность:

${\displaystyle \ell =\sum _{k:y_{k}=1}\ln(p_{k})+\sum _{k:y_{k}=0}\ln(1-p_{k})=\sum _{k=1}^{K}\left(\,y_{k}\ln(p_{k})+(1-y_{k})\ln(1-p_{k})\right)}$

или, что эквивалентно, максимизировать саму функцию правдоподобия , которая представляет собой вероятность того, что данный набор данных создается определенной логистической функцией:

${\displaystyle L=\prod _{k:y_{k}=1}p_{k}\,\prod _{k:y_{k}=0}(1-p_{k})}$

Этот метод известен как оценка максимального правдоподобия .

Оценка параметров

Поскольку ℓ нелинейно по и , определение их оптимальных значений потребует численных методов. Один из методов максимизации ℓ — потребовать, чтобы производные ℓ по и были равны нулю: ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

${\displaystyle 0={\frac {\partial \ell }{\partial \beta _{0}}}=\sum _{k=1}^{K}(y_{k}-p_{k})}$

${\displaystyle 0={\frac {\partial \ell }{\partial \beta _{1}}}=\sum _{k=1}^{K}(y_{k}-p_{k})x_{k}}$

а процедура максимизации может быть выполнена путем решения двух приведенных выше уравнений для и , что, опять же, обычно требует использования численных методов. ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

Значения и которые максимизируют ℓ и L с использованием приведенных выше данных: ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

${\displaystyle \beta _{0}\approx -4.1}$

${\displaystyle \beta _{1}\approx 1.5}$

что дает значение для µ и s :

${\displaystyle \mu =-\beta _{0}/\beta _{1}\approx 2.7}$

${\displaystyle s=1/\beta _{1}\approx 0.67}$

Прогнозы

Коэффициенты и можно ввести в уравнение логистической регрессии, чтобы оценить вероятность сдачи экзамена. ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

Например, для студента, который учится 2 часа, ввод значения в уравнение дает расчетную вероятность сдачи экзамена 0,25: ${\displaystyle x=2}$

${\displaystyle t=\beta _{0}+2\beta _{1}\approx -4.1+2\cdot 1.5=-1.1}$

${\displaystyle p={\frac {1}{1+e^{-t}}}\approx 0.25={\text{Probability of passing exam}}}$

Аналогично, для студента, который учится 4 часа, предполагаемая вероятность сдачи экзамена равна 0,87:

${\displaystyle t=\beta _{0}+4\beta _{1}\approx -4.1+4\cdot 1.5=1.9}$

${\displaystyle p={\frac {1}{1+e^{-t}}}\approx 0.87={\text{Probability of passing exam}}}$

В этой таблице показана предполагаемая вероятность сдачи экзамена при нескольких значениях часов обучения.

Оценка модели

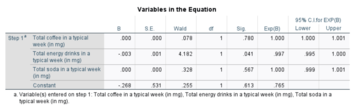
Логистический регрессионный анализ дает следующий результат.

Результаты теста Вальда показывают, что часы обучения значимо связаны с вероятностью сдачи экзамена ( ). Вместо метода Вальда рекомендуемым методом ^[20] расчета значения p для логистической регрессии является тест отношения правдоподобия (LRT), который для этих данных дает (см. § Тесты на отклонение и отношение правдоподобия ниже). ${\displaystyle p=0.017}$ ${\displaystyle p\approx 0.00064}$

Обобщения

Эта простая модель является примером бинарной логистической регрессии и имеет одну объясняющую переменную и двоичную категориальную переменную, которая может принимать одно из двух категориальных значений. Полиномиальная логистическая регрессия — это обобщение бинарной логистической регрессии, включающее любое количество независимых переменных и любое количество категорий.

Фон

Рисунок 1. Стандартная логистическая функция ; для всех . ${\displaystyle \sigma (t)}$ ${\displaystyle \sigma (t)\in (0,1)}$ ${\displaystyle t}$

Определение логистической функции

Объяснение логистической регрессии можно начать с объяснения стандартной логистической функции . Логистическая функция — это сигмовидная функция , которая принимает любые действительные входные данные и выводит значение от нуля до единицы. ^[2] Для логита это интерпретируется как входные логарифмические шансы и выходная вероятность . Стандартная логистическая функция определяется следующим образом : ${\displaystyle t}$ ${\displaystyle \sigma :\mathbb {R} \rightarrow (0,1)}$

${\displaystyle \sigma (t)={\frac {e^{t}}{e^{t}+1}}={\frac {1}{1+e^{-t}}}}$

График логистической функции на t -интервале (−6,6) показан на рисунке 1.

Предположим, что является линейной функцией одной объясняющей переменной (случай, когда является линейной комбинацией нескольких объясняющих переменных, рассматривается аналогично). Тогда мы можем выразить это следующим образом: ${\displaystyle t}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle t}$

${\displaystyle t=\beta _{0}+\beta _{1}x}$

А общую логистическую функцию теперь можно записать как: ${\displaystyle p:\mathbb {R} \rightarrow (0,1)}$

${\displaystyle p(x)=\sigma (t)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}}$

В логистической модели интерпретируется как вероятность того, что зависимая переменная будет равна успеху/случайу, а не неудаче/неслучаю. Понятно, что переменные ответа не распределены одинаково: они различаются от одной точки данных к другой, хотя они независимы, учитывая матрицу плана и общие параметры . ^[11] ${\displaystyle p(x)}$ ${\displaystyle Y}$ ${\displaystyle Y_{i}}$ ${\displaystyle P(Y_{i}=1\mid X)}$ ${\displaystyle X_{i}}$ ${\displaystyle X}$ ${\displaystyle \beta }$

Определение обратной логистической функции

Теперь мы можем определить функцию логит (логарифм шансов) как обратную стандартную логистическую функцию. Легко видеть, что оно удовлетворяет: ${\displaystyle g=\sigma ^{-1}}$

${\displaystyle g(p(x))=\sigma ^{-1}(p(x))=\operatorname {logit} p(x)=\ln \left({\frac {p(x)}{1-p(x)}}\right)=\beta _{0}+\beta _{1}x,}$

и, что эквивалентно, после возведения в степень обеих сторон мы имеем шансы:

${\displaystyle {\frac {p(x)}{1-p(x)}}=e^{\beta _{0}+\beta _{1}x}.}$

Интерпретация этих терминов

В приведенных выше уравнениях члены следующие:

• ${\displaystyle g}$это логит-функция. Уравнение для показывает, что логит (т. е. логарифм шансов или натуральный логарифм шансов) эквивалентен выражению линейной регрессии. ${\displaystyle g(p(x))}$
• ${\displaystyle \ln }$обозначает натуральный логарифм .
• ${\displaystyle p(x)}$— это вероятность того, что зависимая переменная соответствует случаю при некоторой линейной комбинации предикторов. Формула показывает, что вероятность того, что зависимая переменная равна случаю, равна значению логистической функции выражения линейной регрессии. Это важно, поскольку показывает, что значение выражения линейной регрессии может варьироваться от отрицательной до положительной бесконечности, и тем не менее, после преобразования результирующее выражение для вероятности находится в диапазоне от 0 до 1. ${\displaystyle p(x)}$ ${\displaystyle p(x)}$
• ${\displaystyle \beta _{0}}$— это результат уравнения линейной регрессии (значение критерия, когда предиктор равен нулю).
• ${\displaystyle \beta _{1}x}$— коэффициент регрессии, умноженный на некоторое значение предиктора.
• основание обозначает показательную функцию. ${\displaystyle e}$

Определение шансов

Вероятность того, что зависимая переменная равна случаю (при некоторой линейной комбинации предикторов), эквивалентна экспоненциальной функции выражения линейной регрессии. Это иллюстрирует, как логит служит функцией связи между вероятностью и выражением линейной регрессии. Учитывая, что логит находится в диапазоне от отрицательной до положительной бесконечности, он обеспечивает адекватный критерий для проведения линейной регрессии, и логит легко преобразуется обратно в шансы. ^[2] ${\displaystyle x}$

Таким образом, мы определяем вероятность того, что зависимая переменная будет равна случаю (при некоторой линейной комбинации предикторов) следующим образом: ${\displaystyle x}$

${\displaystyle {\text{odds}}=e^{\beta _{0}+\beta _{1}x}.}$

Отношение шансов

Для непрерывной независимой переменной отношение шансов можно определить как:

Изображение представляет собой схему того, как соотношение шансов выглядит в письменной форме, с помощью шаблона в дополнение к примеру результатов теста в разделе «Пример» содержания. Проще говоря, если мы гипотетически получим отношение шансов 2 к 1, мы можем сказать... «Для каждого увеличения количества изучаемых часов на одну единицу шансы сдать (группа 1) или провалить (группа 0) (ожидаемо) ) 2 к 1 (Денис, 2019).

${\displaystyle \mathrm {OR} ={\frac {\operatorname {odds} (x+1)}{\operatorname {odds} (x)}}={\frac {\left({\frac {p(x+1)}{1-p(x+1)}}\right)}{\left({\frac {p(x)}{1-p(x)}}\right)}}={\frac {e^{\beta _{0}+\beta _{1}(x+1)}}{e^{\beta _{0}+\beta _{1}x}}}=e^{\beta _{1}}}$

Эта экспоненциальная зависимость дает интерпретацию : шансы умножаются на каждое увеличение x на 1 единицу. ^[21] ${\displaystyle \beta _{1}}$ ${\displaystyle e^{\beta _{1}}}$

Для двоичной независимой переменной отношение шансов определяется как где a , b , c и d — ячейки в таблице сопряженности 2×2 . ^[22] ${\displaystyle {\frac {ad}{bc}}}$

Несколько независимых переменных

Если имеется несколько независимых переменных, приведенное выше выражение можно изменить на . Затем, когда это используется в уравнении, связывающем логарифм шансов успеха со значениями предикторов, линейная регрессия будет множественной регрессией с m объяснителями; все параметры являются приблизительными. ${\displaystyle \beta _{0}+\beta _{1}x}$ ${\displaystyle \beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m}=\beta _{0}+\sum _{i=1}^{m}\beta _{i}x_{i}}$ ${\displaystyle \beta _{j}}$ ${\displaystyle j=0,1,2,\dots ,m}$

Опять же, более традиционные уравнения:

${\displaystyle \log {\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m}}$

и

${\displaystyle p={\frac {1}{1+b^{-(\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m})}}}}$

где обычно . ${\displaystyle b=e}$

Определение

Основная настройка логистической регрессии заключается в следующем. Нам дан набор данных, содержащий N точек. Каждая точка i состоит из набора m входных переменных x _{1, i} ... x _m,i (также называемых независимыми переменными , объясняющими переменными, переменными-предикторами, признаками или атрибутами) и двоичной выходной переменной Y _i (также известной как как зависимая переменная , переменная ответа, выходная переменная или класс), т. е. она может принимать только два возможных значения: 0 (часто означает «нет» или «неудача») или 1 (часто означает «да» или «успех»). Цель логистической регрессии — использовать набор данных для создания прогнозной модели результирующей переменной.

Как и в линейной регрессии, предполагается, что переменные результата Y _i зависят от объясняющих переменных x _{1, i} ... x _m,i .

Независимые переменные

Независимые переменные могут быть любого типа : действительные , двоичные , категориальные и т. д. Основное различие заключается между непрерывными переменными и дискретными переменными .

(Дискретные переменные, относящиеся к более чем двум возможным вариантам выбора, обычно кодируются с использованием фиктивных переменных (или индикаторных переменных ), то есть для каждого возможного значения дискретной переменной создаются отдельные объясняющие переменные, принимающие значение 0 или 1, причем 1 означает « переменная имеет заданное значение», а 0 означает «переменная не имеет этого значения».)

Итоговые переменные

Формально результаты Y _i описываются как данные , распределенные по Бернулли , где каждый результат определяется ненаблюдаемой вероятностью p _i , которая специфична для рассматриваемого результата, но связана с объясняющими переменными. Это может быть выражено в любой из следующих эквивалентных форм:

${\displaystyle {\begin{aligned}Y_{i}\mid x_{1,i},\ldots ,x_{m,i}\ &\sim \operatorname {Bernoulli} (p_{i})\\\operatorname {\mathbb {E} } [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}]&=p_{i}\\\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&={\begin{cases}p_{i}&{\text{if }}y=1\\1-p_{i}&{\text{if }}y=0\end{cases}}\\\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&=p_{i}^{y}(1-p_{i})^{(1-y)}\end{aligned}}}$

Значения этих четырех строк таковы:

1. Первая строка выражает распределение вероятностей каждого Y _i  : при условии объясняющих переменных оно соответствует распределению Бернулли с параметрами _pi , вероятностью результата 1 для испытания i . Как отмечалось выше, каждое отдельное испытание имеет свою вероятность успеха, так же как каждое испытание имеет свои собственные объясняющие переменные. Вероятность успеха p _i не наблюдается, а только результат отдельного испытания Бернулли с использованием этой вероятности.
2. Вторая строка выражает тот факт, что ожидаемое значение каждого Y _i равно вероятности успеха p _i , что является общим свойством распределения Бернулли. Другими словами, если мы проведем большое количество испытаний Бернулли, используя одну и ту же вероятность успеха p i _, а затем возьмем среднее значение всех исходов 1 и 0, то результат будет близок к pi _. Это связано с тем, что при таком усреднении просто вычисляется доля видимых успехов, которая, как мы ожидаем, будет сходиться с основной вероятностью успеха.
3. Третья строка записывает функцию массы вероятности распределения Бернулли, определяющую вероятность увидеть каждый из двух возможных результатов.
4. Четвертая строка — это еще один способ записи функции массы вероятности, который позволяет избежать написания отдельных случаев и более удобен для определенных типов вычислений. Это основано на том, что Y _i может принимать только значение 0 или 1. В каждом случае один из показателей степени будет равен 1, «выбирая» значение под ним, а другой равен 0, «отменяя» значение под ним. это. Следовательно, результатом будет либо p _i , либо 1 −  p _i , как в предыдущей строке.

Функция линейного прогнозирования

Основная идея логистической регрессии заключается в использовании механизма, уже разработанного для линейной регрессии , путем моделирования вероятности p _i с использованием линейной предикторной функции , то есть линейной комбинации объясняющих переменных и набора коэффициентов регрессии , специфичных для рассматриваемой модели. но то же самое для всех испытаний. Функция линейного прогнозирования для конкретной точки данных i записывается как: ${\displaystyle f(i)}$

${\displaystyle f(i)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{m}x_{m,i},}$

где – коэффициенты регрессии , указывающие относительное влияние конкретной объясняющей переменной на результат. ${\displaystyle \beta _{0},\ldots ,\beta _{m}}$

Модель обычно придают более компактную форму следующим образом:

• Коэффициенты регрессии β ₀ , β ₁ , ..., β _m группируются в один вектор β размера m  + 1.
• Для каждой точки данных i добавляется дополнительная поясняющая псевдопеременная x _{0, i} с фиксированным значением 1, соответствующим коэффициенту пересечения β ₀ .
• Полученные объясняющие переменные x _{0, i} , x _{1, i} , ..., x _m,i затем группируются в один вектор X _i размера m  + 1.

Это позволяет записать функцию линейного предиктора следующим образом:

${\displaystyle f(i)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i},}$

используя обозначение скалярного произведения между двумя векторами.

Это пример выходных данных SPSS для модели логистической регрессии с использованием трех объясняющих переменных (употребление кофе в неделю, употребление энергетических напитков в неделю и употребление газированных напитков в неделю) и двух категорий (мужчины и женщины).

Множество объясняющих переменных, две категории

Приведенный выше пример бинарной логистической регрессии с одной независимой переменной можно обобщить до бинарной логистической регрессии с любым количеством объясняющих переменных x ₁ , x ₂ ,... и любым количеством категориальных значений . ${\displaystyle y=0,1,2,\dots }$

Для начала мы можем рассмотреть логистическую модель с M объясняющими переменными x ₁ , x ₂ ... x _M и, как в приведенном выше примере, двумя категориальными значениями ( y = 0 и 1). Для простой модели бинарной логистической регрессии мы предположили линейную зависимость между переменной-предиктором и логарифмом шансов (также называемым logit ) события, которое . Эту линейную зависимость можно распространить на случай M объясняющих переменных: ${\displaystyle y=1}$

${\displaystyle t=\log _{b}{\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{M}x_{M}}$

где t — логарифм шансов, а — параметры модели. Введено дополнительное обобщение, в котором база модели ( b ) не ограничивается числом Эйлера e . В большинстве приложений основание логарифма обычно принимается равным e . Однако в некоторых случаях может быть проще сообщить результаты, работая по основанию 2 или 10. ${\displaystyle \beta _{i}}$ ${\displaystyle b}$

Для более компактных обозначений мы зададим объясняющие переменные и коэффициенты β как -мерные векторы: ${\displaystyle (M+1)}$

${\displaystyle {\boldsymbol {x}}=\{x_{0},x_{1},x_{2},\dots ,x_{M}\}}$

${\displaystyle {\boldsymbol {\beta }}=\{\beta _{0},\beta _{1},\beta _{2},\dots ,\beta _{M}\}}$

с добавленной объясняющей переменной x ₀ =1. Логит теперь может быть записан как:

${\displaystyle t=\sum _{m=0}^{M}\beta _{m}x_{m}={\boldsymbol {\beta }}\cdot x}$

Решение для вероятности p , которое дает: ${\displaystyle y=1}$

${\displaystyle p({\boldsymbol {x}})={\frac {b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}{1+b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}}={\frac {1}{1+b^{-{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}}=S_{b}(t)}$,

где сигмовидная функция с основанием . Приведенная выше формула показывает, что как только они фиксированы, мы можем легко вычислить либо логарифм шансов для данного наблюдения, либо вероятность для данного наблюдения. Основной вариант использования логистической модели — получить наблюдение и оценить вероятность того, что . Оптимальные бета-коэффициенты снова могут быть найдены путем максимизации логарифмического правдоподобия. Для K измерений, определяемых как объясняющий вектор k -го измерения и как категориальный результат этого измерения, логарифмическое правдоподобие может быть записано в форме, очень похожей на простой случай, описанный выше: ${\displaystyle S_{b}}$ ${\displaystyle b}$ ${\displaystyle \beta _{m}}$ ${\displaystyle y=1}$ ${\displaystyle y=1}$ ${\displaystyle {\boldsymbol {x}}}$ ${\displaystyle p({\boldsymbol {x}})}$ ${\displaystyle y=1}$ ${\displaystyle {\boldsymbol {x}}_{k}}$ ${\displaystyle y_{k}}$ ${\displaystyle M=1}$

${\displaystyle \ell =\sum _{k=1}^{K}y_{k}\log _{b}(p({\boldsymbol {x_{k}}}))+\sum _{k=1}^{K}(1-y_{k})\log _{b}(1-p({\boldsymbol {x_{k}}}))}$

Как и в простом примере выше, для поиска оптимальных параметров β потребуются численные методы. Одним из полезных методов является приравнивание производных логарифмического правдоподобия по каждому из параметров β нулю, что дает набор уравнений, которые будут выполняться при максимуме логарифмического правдоподобия:

${\displaystyle {\frac {\partial \ell }{\partial \beta _{m}}}=0=\sum _{k=1}^{K}y_{k}x_{mk}-\sum _{k=1}^{K}p({\boldsymbol {x}}_{k})x_{mk}}$

где x _mk — значение объясняющей переменной x _m по k-му измерению.

Рассмотрим пример с объясняющими переменными , и коэффициентами , , и которые были определены указанным выше методом. Если быть более конкретным, то модель такова: ${\displaystyle M=2}$ ${\displaystyle b=10}$ ${\displaystyle \beta _{0}=-3}$ ${\displaystyle \beta _{1}=1}$ ${\displaystyle \beta _{2}=2}$

${\displaystyle t=\log _{10}{\frac {p}{1-p}}=-3+x_{1}+2x_{2}}$

${\displaystyle p={\frac {b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}{1+b^{{\boldsymbol {\beta }}\cdot x}}}={\frac {b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}{1+b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}}={\frac {1}{1+b^{-(\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2})}}}}$,

где p — вероятность того, что . Это можно интерпретировать следующим образом: ${\displaystyle y=1}$

• ${\displaystyle \beta _{0}=-3}$это y -перехват . Это логарифмические шансы события , когда предикторы . Возведя в степень, мы можем увидеть, что, когда шансы события составляют от 1 до 1000 или . Аналогичным образом, вероятность события « когда» может быть вычислена как ${\displaystyle y=1}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle y=1}$ ${\displaystyle 10^{-3}}$ ${\displaystyle y=1}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle 1/(1000+1)=1/1001.}$
• ${\displaystyle \beta _{1}=1}$означает, что увеличение на 1 увеличивает логарифмические шансы на . Таким образом , при увеличении на 1 шансы увеличиваются в . Вероятность также увеличилась , но она не увеличилась настолько, насколько увеличились шансы . ${\displaystyle x_{1}}$ ${\displaystyle 1}$ ${\displaystyle x_{1}}$ ${\displaystyle y=1}$ ${\displaystyle 10^{1}}$ ${\displaystyle y=1}$
• ${\displaystyle \beta _{2}=2}$означает, что увеличение на 1 увеличивает логарифмические шансы на . Таким образом , при увеличении на 1 шансы увеличиваются в раз. Обратите внимание, что влияние на логарифм шансов в два раза больше, чем влияние , но влияние на шансы в 10 раз больше. Но влияние на вероятность не в 10 раз больше, а только на шансы в 10 раз больше. ${\displaystyle x_{2}}$ ${\displaystyle 2}$ ${\displaystyle x_{2}}$ ${\displaystyle y=1}$ ${\displaystyle 10^{2}.}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{1}}$ ${\displaystyle y=1}$

Полиномиальная логистическая регрессия: множество объясняющих переменных и множество категорий.

В приведенных выше случаях двух категорий (биномиальная логистическая регрессия) категории были проиндексированы «0» и «1», и у нас было две вероятности: вероятность того, что результат находился в категории 1, определялась как и вероятность того, что результат находился в категории 0, был предоставлен . Сумма этих вероятностей равна 1, что должно быть правдой, поскольку «0» и «1» — единственные возможные категории в этой настройке. ${\displaystyle p({\boldsymbol {x}})}$ ${\displaystyle 1-p({\boldsymbol {x}})}$

В общем, если у нас есть объясняющие переменные (включая x ₀ ) и категории, нам потребуются отдельные вероятности, по одной для каждой категории, индексированные n , которые описывают вероятность того, что категориальный результат y будет находиться в категории y=n , при условии, что вектор ковариат x . Сумма этих вероятностей по всем категориям должна равняться 1. Используя математически удобную базу e , эти вероятности равны: ${\displaystyle M+1}$ ${\displaystyle N+1}$ ${\displaystyle N+1}$

${\displaystyle p_{n}({\boldsymbol {x}})={\frac {e^{{\boldsymbol {\beta }}_{n}\cdot {\boldsymbol {x}}}}{1+\sum _{u=1}^{N}e^{{\boldsymbol {\beta }}_{u}\cdot {\boldsymbol {x}}}}}}$для ${\displaystyle n=1,2,\dots ,N}$

${\displaystyle p_{0}({\boldsymbol {x}})=1-\sum _{n=1}^{N}p_{n}({\boldsymbol {x}})={\frac {1}{1+\sum _{u=1}^{N}e^{{\boldsymbol {\beta }}_{u}\cdot {\boldsymbol {x}}}}}}$

Каждая из вероятностей, кроме, будет иметь свой собственный набор коэффициентов регрессии . Можно видеть, что, как и требовалось, сумма по всем категориям n равна 1. Выбор для определения через другие вероятности является искусственным. Любая из вероятностей могла быть выбрана для такого определения. Это особое значение n называется «индексом поворота», а логарифмические шансы ( t _n ) выражаются через вероятность поворота и снова выражаются как линейная комбинация объясняющих переменных: ${\displaystyle p_{0}({\boldsymbol {x}})}$ ${\displaystyle {\boldsymbol {\beta }}_{n}}$ ${\displaystyle p_{n}({\boldsymbol {x}})}$ ${\displaystyle p_{0}({\boldsymbol {x}})}$

${\displaystyle t_{n}=\ln \left({\frac {p_{n}({\boldsymbol {x}})}{p_{0}({\boldsymbol {x}})}}\right)={\boldsymbol {\beta }}_{n}\cdot {\boldsymbol {x}}}$

Обратите также внимание, что для простого случая , восстанавливается случай двух категорий с и . ${\displaystyle N=1}$ ${\displaystyle p({\boldsymbol {x}})=p_{1}({\boldsymbol {x}})}$ ${\displaystyle p_{0}({\boldsymbol {x}})=1-p_{1}({\boldsymbol {x}})}$

Теперь можно вычислить логарифмическую вероятность того, что конкретный набор K измерений или точек данных будет сгенерирован вышеуказанными вероятностями. Индексируя каждое измерение посредством k , обозначим k -й набор измеряемых объясняющих переменных через , а их категориальные результаты — через которые могут быть равны любому целому числу из [0,N]. Логарифмическая вероятность тогда равна: ${\displaystyle {\boldsymbol {x}}_{k}}$ ${\displaystyle y_{k}}$

${\displaystyle \ell =\sum _{k=1}^{K}\sum _{n=0}^{N}\Delta (n,y_{k})\,\ln(p_{n}({\boldsymbol {x}}_{k}))}$

где – индикаторная функция , равная 1, если y _k = n , и нулю в противном случае. В случае двух объясняющих переменных эта индикаторная функция определялась как y _k при n = 1 и 1-y _k при n = 0. Это было удобно, но не обязательно. ^[23] Опять же, оптимальные бета-коэффициенты могут быть найдены путем максимизации логарифмической функции правдоподобия, обычно с использованием численных методов. Возможный метод решения состоит в том, чтобы установить производные логарифмического правдоподобия по каждому бета-коэффициенту равными нулю и найти бета-коэффициенты: ${\displaystyle \Delta (n,y_{k})}$

${\displaystyle {\frac {\partial \ell }{\partial \beta _{nm}}}=0=\sum _{k=1}^{K}\Delta (n,y_{k})x_{mk}-\sum _{k=1}^{K}p_{n}({\boldsymbol {x}}_{k})x_{mk}}$

где – m -й коэффициент вектора и – m -я объясняющая переменная k -го измерения. Как только бета-коэффициенты будут оценены на основе данных, мы сможем оценить вероятность того, что любой последующий набор объясняющих переменных приведет к любой из возможных категорий результатов. ${\displaystyle \beta _{nm}}$ ${\displaystyle {\boldsymbol {\beta }}_{n}}$ ${\displaystyle x_{mk}}$

Интерпретации

Существуют различные эквивалентные спецификации и интерпретации логистической регрессии, которые вписываются в разные типы более общих моделей и допускают различные обобщения.

Как обобщенная линейная модель

Конкретная модель, используемая логистической регрессией, которая отличает ее от стандартной линейной регрессии и от других типов регрессионного анализа , используемых для двоичных результатов, представляет собой способ, которым вероятность конкретного результата связана с функцией линейного предиктора:

${\displaystyle \operatorname {logit} (\operatorname {\mathbb {E} } [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}])=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{m}x_{m,i}}$

Написанное с использованием более компактной записи, описанной выше, это:

${\displaystyle \operatorname {logit} (\operatorname {\mathbb {E} } [Y_{i}\mid \mathbf {X} _{i}])=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}$

Эта формулировка выражает логистическую регрессию как тип обобщенной линейной модели , которая предсказывает переменные с различными типами распределений вероятностей , подгоняя линейную предикторную функцию вышеуказанной формы к некоторому произвольному преобразованию ожидаемого значения переменной.

Интуитивный подход к преобразованию с использованием функции logit (натуральный логарифм шансов) был объяснен выше ^{[ необходимы пояснения ]} . Это также имеет практический эффект преобразования вероятности (которая ограничена диапазоном от 0 до 1) в переменную, которая находится в диапазоне более - тем самым согласовывая потенциальный диапазон функции линейного прогнозирования в правой части уравнения. ${\displaystyle (-\infty ,+\infty )}$

И вероятности pi _, и коэффициенты регрессии не наблюдаются, и средства их определения не являются частью самой модели. Обычно они определяются с помощью какой-либо процедуры оптимизации, например, оценки максимального правдоподобия , которая находит значения, которые лучше всего соответствуют наблюдаемым данным (т. е. которые дают наиболее точные прогнозы для уже наблюдаемых данных), обычно с учетом условий регуляризации , которые стремятся исключить маловероятные данные. значения, например чрезвычайно большие значения для любого из коэффициентов регрессии. Использование условия регуляризации эквивалентно выполнению максимальной апостериорной оценки (MAP), что является расширением метода максимального правдоподобия. (Регуляризация чаще всего выполняется с использованием квадратичной функции регуляризации , которая эквивалентна размещению априорного распределения Гаусса с нулевым средним на коэффициентах, но возможны и другие регуляризаторы.) Независимо от того, используется ли регуляризация, обычно невозможно найти решение закрытой формы; вместо этого необходимо использовать итерационный численный метод, такой как итеративно перевзвешенный метод наименьших квадратов (IRLS) или, что чаще встречается в наши дни, квазиньютоновский метод, такой как метод L-BFGS . ^[24]

Интерпретация оценок параметра β _j заключается в аддитивном влиянии на логарифм шансов единичного изменения объясняющей переменной j . Например, в случае дихотомической объясняющей переменной пол — это оценка шансов на достижение результата, скажем, для мужчин по сравнению с женщинами. ${\displaystyle e^{\beta }}$

Эквивалентная формула использует обратную функцию логит, которая является логистической функцией , т.е.:

${\displaystyle \operatorname {\mathbb {E} } [Y_{i}\mid \mathbf {X} _{i}]=p_{i}=\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})={\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}}$

Формулу также можно записать в виде распределения вероятностей (в частности, с использованием функции массы вероятности ):

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={p_{i}}^{y}(1-p_{i})^{1-y}=\left({\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{y}\left(1-{\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{1-y}={\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\cdot y}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}}$

Как модель со скрытыми переменными

Логистическая модель имеет эквивалентную формулировку как модель со скрытыми переменными . Эта формулировка распространена в теории моделей дискретного выбора и позволяет легко расширить ее до некоторых более сложных моделей с множественным коррелированным выбором, а также сравнить логистическую регрессию с тесно связанной пробит-моделью .

Представьте, что для каждого испытания i существует непрерывная скрытая переменная Y _i ^* (т. е. ненаблюдаемая случайная величина ), которая распределяется следующим образом:

${\displaystyle Y_{i}^{\ast }={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon _{i}\,}$

где

${\displaystyle \varepsilon _{i}\sim \operatorname {Logistic} (0,1)\,}$

т.е. скрытая переменная может быть записана непосредственно через функцию линейного прогнозирования и аддитивную переменную случайной ошибки , которая распределяется в соответствии со стандартным логистическим распределением .

Тогда Y _i можно рассматривать как индикатор того, является ли эта скрытая переменная положительной:

${\displaystyle Y_{i}={\begin{cases}1&{\text{if }}Y_{i}^{\ast }>0\ {\text{ i.e. }}-\varepsilon _{i}<{\boldsymbol {\beta }}\cdot \mathbf {X} _{i},\\0&{\text{otherwise.}}\end{cases}}}$

Выбор моделирования переменной ошибки конкретно со стандартным логистическим распределением, а не с общим логистическим распределением с произвольными значениями местоположения и масштаба, кажется ограничительным, но на самом деле это не так. Следует иметь в виду, что мы можем сами выбирать коэффициенты регрессии и очень часто использовать их для компенсации изменений параметров распределения переменной ошибки. Например, распределение логистической переменной ошибки с ненулевым параметром местоположения μ (который устанавливает среднее значение) эквивалентно распределению с нулевым параметром местоположения, где μ был добавлен к коэффициенту пересечения. Обе ситуации дают одно и то же значение Y _i ^* независимо от настроек объясняющих переменных. Аналогично, произвольный параметр масштаба s эквивалентен установке параметра масштаба на 1, а затем делению всех коэффициентов регрессии на s . В последнем случае результирующее значение Y _i ^* будет в s раз меньше , чем в первом случае, для всех наборов объясняющих переменных — но, что критически важно, оно всегда будет оставаться по ту же сторону от 0 и, следовательно, вести к тому же Y _я выбор.

(Это предсказывает, что нерелевантность параметра масштаба может не распространяться на более сложные модели, в которых доступно более двух вариантов.)

Оказывается, эта формулировка в точности эквивалентна предыдущей, сформулированной в терминах обобщенной линейной модели и без каких-либо скрытых переменных . Это можно показать следующим образом, используя тот факт, что кумулятивная функция распределения (CDF) стандартного логистического распределения представляет собой логистическую функцию , которая является обратной логит -функцией , т.е.

${\displaystyle \Pr(\varepsilon _{i}<x)=\operatorname {logit} ^{-1}(x)}$

Затем:

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1\mid \mathbf {X} _{i})&=\Pr(Y_{i}^{\ast }>0\mid \mathbf {X} _{i})\\[5pt]&=\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon _{i}>0)\\[5pt]&=\Pr(\varepsilon _{i}>-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]&=\Pr(\varepsilon _{i}<{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(because the logistic distribution is symmetric)}}\\[5pt]&=\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&\\[5pt]&=p_{i}&&{\text{(see above)}}\end{aligned}}}$

Эта формулировка, которая является стандартной в моделях дискретного выбора , проясняет связь между логистической регрессией («логит-моделью») и пробит-моделью , которая использует переменную ошибки, распределенную в соответствии со стандартным нормальным распределением вместо стандартного логистического распределения. И логистическое, и нормальное распределения симметричны и имеют базовую унимодальную форму «колокола». Единственное отличие состоит в том, что логистическое распределение имеет несколько более тяжелые хвосты , что означает, что оно менее чувствительно к посторонним данным (и, следовательно, несколько более устойчиво к моделированию неправильных спецификаций или ошибочных данных).

Двусторонняя модель со скрытыми переменными

Еще одна формулировка использует две отдельные скрытые переменные:

${\displaystyle {\begin{aligned}Y_{i}^{0\ast }&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\varepsilon _{0}\,\\Y_{i}^{1\ast }&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}+\varepsilon _{1}\,\end{aligned}}}$

где

${\displaystyle {\begin{aligned}\varepsilon _{0}&\sim \operatorname {EV} _{1}(0,1)\\\varepsilon _{1}&\sim \operatorname {EV} _{1}(0,1)\end{aligned}}}$

где EV ₁ (0,1) — стандартное распределение экстремальных значений типа 1 : т.е.

${\displaystyle \Pr(\varepsilon _{0}=x)=\Pr(\varepsilon _{1}=x)=e^{-x}e^{-e^{-x}}}$

Затем

${\displaystyle Y_{i}={\begin{cases}1&{\text{if }}Y_{i}^{1\ast }>Y_{i}^{0\ast },\\0&{\text{otherwise.}}\end{cases}}}$

Эта модель имеет отдельную скрытую переменную и отдельный набор коэффициентов регрессии для каждого возможного результата зависимой переменной. Причина такого разделения в том, что оно позволяет легко распространить логистическую регрессию на категориальные переменные с несколькими исходами, как в полиномиальной логит- модели. В такой модели естественно моделировать каждый возможный результат, используя другой набор коэффициентов регрессии. Также возможно мотивировать каждую из отдельных скрытых переменных как теоретическую полезность , связанную с совершением соответствующего выбора, и, таким образом, мотивировать логистическую регрессию с точки зрения теории полезности . (С точки зрения теории полезности, рациональный субъект всегда выбирает выбор с наибольшей связанной с ним полезностью.) Это подход, используемый экономистами при формулировании моделей дискретного выбора , поскольку он одновременно обеспечивает теоретически прочную основу и облегчает интуитивное представление о модели, которая в свою очередь, позволяет легко рассматривать различные виды расширений. (См. пример ниже.)

Выбор распределения экстремальных значений типа 1 кажется довольно произвольным, но он заставляет математически работать, и его использование может быть возможно оправдать с помощью теории рационального выбора .

Оказывается, эта модель эквивалентна предыдущей модели, хотя это кажется неочевидным, поскольку теперь существует два набора коэффициентов регрессии и переменных ошибок, а переменные ошибок имеют другое распределение. Фактически эта модель сводится непосредственно к предыдущей со следующими заменами:

${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}}$

Интуитивное понимание этого исходит из того факта, что, поскольку мы выбираем, основываясь максимум на двух значениях, имеет значение только их разница, а не точные значения — и это эффективно удаляет одну степень свободы . Еще одним важным фактом является то, что разница двух переменных с распределением экстремальных значений типа 1 представляет собой логистическое распределение, т. е. мы можем продемонстрировать эквивалент следующим образом: ${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}\sim \operatorname {Logistic} (0,1).}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1\mid \mathbf {X} _{i})={}&\Pr \left(Y_{i}^{1\ast }>Y_{i}^{0\ast }\mid \mathbf {X} _{i}\right)&\\[5pt]={}&\Pr \left(Y_{i}^{1\ast }-Y_{i}^{0\ast }>0\mid \mathbf {X} _{i}\right)&\\[5pt]={}&\Pr \left({\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}+\varepsilon _{1}-\left({\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\varepsilon _{0}\right)>0\right)&\\[5pt]={}&\Pr \left(({\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}-{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i})+(\varepsilon _{1}-\varepsilon _{0})>0\right)&\\[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0})\cdot \mathbf {X} _{i}+(\varepsilon _{1}-\varepsilon _{0})>0)&\\[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0})\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(substitute }}\varepsilon {\text{ as above)}}\\[5pt]={}&\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(substitute }}{\boldsymbol {\beta }}{\text{ as above)}}\\[5pt]={}&\Pr(\varepsilon >-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(now, same as above model)}}\\[5pt]={}&\Pr(\varepsilon <{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&\\[5pt]={}&\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]={}&p_{i}\end{aligned}}}$

Пример

В качестве примера рассмотрим выборы на уровне провинции, на которых стоит выбор между правоцентристской партией, левоцентристской партией и сепаратистской партией (например, Квебекская партия , которая хочет отделения Квебека от Канады ). Затем мы использовали бы три скрытые переменные, по одной для каждого выбора. Затем, в соответствии с теорией полезности , мы можем интерпретировать скрытые переменные как выражение полезности , возникающей в результате каждого из выборов. Мы также можем интерпретировать коэффициенты регрессии как указывающие на силу, которую связанный фактор (т. е. объясняющая переменная) оказывает на полезность — или, точнее, на величину, на которую изменение единицы объясняющей переменной меняет полезность данного выбора. Избиратель мог бы ожидать, что правоцентристская партия снизит налоги, особенно для богатых людей. Это не дало бы людям с низкими доходами никакой выгоды, т.е. никакого изменения в полезности (поскольку они обычно не платят налоги); принесет умеренную выгоду (т.е. несколько больше денег или умеренное увеличение полезности) для людей со средним доходом; принесет значительные выгоды людям с высокими доходами. С другой стороны, можно было бы ожидать, что левоцентристская партия повысит налоги и компенсирует это увеличением благосостояния и другой помощью для низших и средних классов. Это принесет значительную положительную выгоду людям с низкими доходами, возможно, слабую выгоду людям со средним доходом и значительную отрицательную выгоду людям с высокими доходами. Наконец, сепаратистская партия не будет предпринимать прямых действий в отношении экономики, а просто отделится. Избиратель с низким или средним доходом может не ожидать от этого явного выигрыша или убытка от полезности, но избиратель с высоким доходом может ожидать отрицательной полезности, поскольку он/она, скорее всего, будет владеть компаниями, которым будет труднее вести бизнес в стране. такая среда и, вероятно, потеряете деньги.

Эти интуиции можно выразить следующим образом:

Это ясно показывает, что

1. Для каждого выбора должны существовать отдельные наборы коэффициентов регрессии. Если говорить с точки зрения полезности, это можно увидеть очень легко. Разные варианты выбора по-разному влияют на чистую полезность; более того, эффекты варьируются сложным образом и зависят от характеристик каждого человека, поэтому для каждой характеристики должны быть отдельные наборы коэффициентов, а не просто одна дополнительная характеристика для каждого выбора.
2. Хотя доход является непрерывной переменной, его влияние на полезность слишком сложно, чтобы его можно было рассматривать как одну переменную. Либо его необходимо напрямую разделить на диапазоны, либо необходимо добавить более высокие степени дохода, чтобы эффективно выполнить полиномиальную регрессию по доходу.

В качестве «логарифмически-линейной» модели

Еще одна формулировка объединяет приведенную выше формулировку двусторонней скрытой переменной с исходной формулировкой выше без скрытых переменных и в процессе обеспечивает ссылку на одну из стандартных формулировок полиномиального логита .

Здесь вместо того, чтобы записывать логит вероятностей pi _как линейный предиктор, мы разделяем линейный предиктор на два, по одному для каждого из двух результатов:

${\displaystyle {\begin{aligned}\ln \Pr(Y_{i}=0)&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}-\ln Z\\\ln \Pr(Y_{i}=1)&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}-\ln Z\end{aligned}}}$

Были введены два отдельных набора коэффициентов регрессии, как и в модели двусторонней скрытой переменной, и два уравнения имеют форму, которая записывает логарифм связанной вероятности как линейный предиктор с дополнительным членом в конце. Этот член, как выясняется, служит нормирующим фактором , гарантирующим, что результат является распределением. Это можно увидеть, возведя в степень обе стороны: ${\displaystyle -\ln Z}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=0)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}\\[5pt]\Pr(Y_{i}=1)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}\end{aligned}}}$

В этой форме ясно, что цель Z состоит в том, чтобы гарантировать, что результирующее распределение по Y _i на самом деле является распределением вероятностей , т. е. его сумма равна 1. Это означает, что Z является просто суммой всех ненормализованных вероятностей, и разделив каждую вероятность на Z , вероятности становятся « нормализованными ». То есть:

${\displaystyle Z=e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}$

и полученные уравнения имеют вид

${\displaystyle {\begin{aligned}\Pr(Y_{i}=0)&={\frac {e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}\\[5pt]\Pr(Y_{i}=1)&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}.\end{aligned}}}$

Или вообще:

${\displaystyle \Pr(Y_{i}=c)={\frac {e^{{\boldsymbol {\beta }}_{c}\cdot \mathbf {X} _{i}}}{\sum _{h}e^{{\boldsymbol {\beta }}_{h}\cdot \mathbf {X} _{i}}}}}$

Это ясно показывает, как обобщить эту формулировку на более чем два результата, как в случае с полиномиальным логитом . Эта общая формулировка представляет собой в точности функцию softmax , как в

${\displaystyle \Pr(Y_{i}=c)=\operatorname {softmax} (c,{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i},{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i},\dots ).}$

Чтобы доказать, что это эквивалентно предыдущей модели, приведенная выше модель является чрезмерно уточненной, поскольку ее нельзя определить независимо: скорее , знание одного автоматически определяет другое. В результате модель становится неидентифицируемой , поскольку множественные комбинации β ₀ и β ₁ будут давать одинаковые вероятности для всех возможных объясняющих переменных. Фактически, можно видеть, что добавление любого постоянного вектора к ним обоим даст одинаковые вероятности: ${\displaystyle \Pr(Y_{i}=0)}$ ${\displaystyle \Pr(Y_{i}=1)}$ ${\displaystyle \Pr(Y_{i}=0)+\Pr(Y_{i}=1)=1}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1)&={\frac {e^{({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}{e^{({\boldsymbol {\beta }}_{0}+\mathbf {C} )\cdot \mathbf {X} _{i}}+e^{({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}}\\[5pt]&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}}\\[5pt]&={\frac {e^{\mathbf {C} \cdot \mathbf {X} _{i}}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{\mathbf {C} \cdot \mathbf {X} _{i}}(e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}})}}\\[5pt]&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}.\end{aligned}}}$

В результате мы можем упростить ситуацию и восстановить идентифицируемость, выбрав произвольное значение для одного из двух векторов. Мы решили установить Тогда, ${\displaystyle {\boldsymbol {\beta }}_{0}=\mathbf {0} .}$

${\displaystyle e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}=e^{\mathbf {0} \cdot \mathbf {X} _{i}}=1}$

и так

${\displaystyle \Pr(Y_{i}=1)={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}={\frac {1}{1+e^{-{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}=p_{i}}$

что показывает, что эта формулировка действительно эквивалентна предыдущей формулировке. (Как и в формулировке двусторонней скрытой переменной, любые настройки будут давать эквивалентные результаты.) ${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

Большинство трактовок полиномиальной логит- модели начинаются либо с расширения представленной здесь «логарифмически-линейной» формулировки, либо с формулировки двусторонней латентной переменной, представленной выше, поскольку обе ясно показывают, как модель может быть расширена до многосторонних результатов. В целом, представление со скрытыми переменными более распространено в эконометрике и политологии , где господствуют модели дискретного выбора и теория полезности , в то время как «логарифмически-линейная» формулировка здесь более распространена в информатике , например, машинном обучении и обработке естественного языка .

Как однослойный перцептрон

Модель имеет эквивалентную формулировку

${\displaystyle p_{i}={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i})}}}.\,}$

Эту функциональную форму обычно называют однослойным перцептроном или однослойной искусственной нейронной сетью . Однослойная нейронная сеть вычисляет непрерывный результат вместо ступенчатой ​​функции . Производная p _i по X  = ( x ₁ , ..., x _k ) вычисляется по общей форме:

${\displaystyle y={\frac {1}{1+e^{-f(X)}}}}$

где f ( X ) — аналитическая функция от X. При таком выборе однослойная нейронная сеть идентична модели логистической регрессии. Эта функция имеет непрерывную производную, что позволяет использовать ее в обратном распространении ошибки . Эта функция предпочтительна еще и потому, что ее производная легко вычисляется:

${\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} X}}=y(1-y){\frac {\mathrm {d} f}{\mathrm {d} X}}.\,}$

С точки зрения биномиальных данных

Тесно связанная модель предполагает, что каждое i связано не с одним испытанием Бернулли, а с n _i независимыми одинаково распределенными испытаниями, где наблюдение Y _i представляет собой количество наблюдаемых успехов (сумма отдельных случайных величин с распределением Бернулли), и отсюда следует биномиальное распределение :

${\displaystyle Y_{i}\,\sim \operatorname {Bin} (n_{i},p_{i}),{\text{ for }}i=1,\dots ,n}$

Примером такого распределения является доля семян ( pi ₎ , которые прорастают после посадки n _{i .}

С точки зрения ожидаемых значений эта модель выражается следующим образом:

${\displaystyle p_{i}=\operatorname {\mathbb {E} } \left[\left.{\frac {Y_{i}}{n_{i}}}\,\right|\,\mathbf {X} _{i}\right]\,,}$

так что

${\displaystyle \operatorname {logit} \left(\operatorname {\mathbb {E} } \left[\left.{\frac {Y_{i}}{n_{i}}}\,\right|\,\mathbf {X} _{i}\right]\right)=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\,,}$

Или эквивалентно:

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={n_{i} \choose y}p_{i}^{y}(1-p_{i})^{n_{i}-y}={n_{i} \choose y}\left({\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{y}\left(1-{\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{n_{i}-y}\,.}$

Эта модель может быть адаптирована с использованием тех же методов, что и приведенная выше более базовая модель.

Примерка модели

Оценка максимального правдоподобия (MLE)

Коэффициенты регрессии обычно оцениваются с использованием оценки максимального правдоподобия . ^{[25] [26]} В отличие от линейной регрессии с нормально распределенными остатками, невозможно найти выражение в замкнутой форме для значений коэффициентов, которые максимизируют функцию правдоподобия, поэтому вместо этого необходимо использовать итерационный процесс; например метод Ньютона . Этот процесс начинается с предварительного решения, его слегка пересматривают, чтобы увидеть, можно ли его улучшить, и повторяют этот пересмотр до тех пор, пока улучшения не перестанут вноситься, после чего говорят, что процесс сошелся. ^[25]

В некоторых случаях модель может не достичь сходимости. Несходимость модели указывает на то, что коэффициенты не имеют смысла, поскольку итерационный процесс не смог найти подходящие решения. Неспособность сходиться может произойти по ряду причин: большое соотношение предикторов к случаям, мультиколлинеарность , разреженность или полное разделение .

• Большое соотношение переменных к случаям приводит к чрезмерно консервативной статистике Вальда (обсуждается ниже) и может привести к несходимости. Регуляризованная логистическая регрессия специально предназначена для использования в этой ситуации.
• Мультиколлинеарность относится к неприемлемо высоким корреляциям между предикторами. По мере увеличения мультиколлинеарности коэффициенты остаются несмещенными, но стандартные ошибки увеличиваются, а вероятность сходимости модели снижается. ^[25] Чтобы обнаружить мультиколлинеарность среди предикторов, можно провести линейный регрессионный анализ интересующих предикторов с единственной целью — изучить статистику толерантности ^[25] , используемую для оценки того, является ли мультиколлинеарность неприемлемо высокой.
• Разреженность данных означает наличие большой доли пустых ячеек (ячейок с нулевым количеством). Нулевое количество ячеек особенно проблематично для категориальных предикторов. При использовании непрерывных предикторов модель может выводить значения для нулевого количества ячеек, но это не относится к категориальным предикторам. Модель не будет сходиться с нулевым количеством ячеек для категориальных предикторов, поскольку натуральный логарифм нуля является неопределенным значением, поэтому окончательное решение модели не может быть достигнуто. Чтобы решить эту проблему, исследователи могут сжимать категории теоретически осмысленным способом или добавлять константы во все ячейки. ^[25]
• Другая числовая проблема, которая может привести к отсутствию сходимости, — это полное разделение, которое относится к случаю, когда предикторы идеально предсказывают критерий — все случаи точно классифицируются, а вероятность максимизируется с помощью бесконечных коэффициентов. В таких случаях следует перепроверить данные, так как может быть какая-то ошибка. ^{[2] [ нужны дополнительные пояснения ]}
• Можно также использовать полупараметрические или непараметрические подходы, например, с помощью методов локального правдоподобия или непараметрических методов квазиправдоподобия, которые избегают предположений о параметрической форме индексной функции и устойчивы к выбору функции связи (например, пробит или логит). ^[27]

Итеративно перевзвешенный метод наименьших квадратов (IRLS)

Бинарная логистическая регрессия ( или ) может, например, быть рассчитана с использованием итеративно перевзвешенного метода наименьших квадратов (IRLS), что эквивалентно максимизации логарифмического правдоподобия распределенного процесса Бернулли с использованием метода Ньютона . Если задача записана в виде векторной матрицы с параметрами , объясняющими переменными и ожидаемым значением распределения Бернулли , параметры можно найти с помощью следующего итерационного алгоритма: ${\displaystyle y=0}$ ${\displaystyle y=1}$ ${\displaystyle \mathbf {w} ^{T}=[\beta _{0},\beta _{1},\beta _{2},\ldots ]}$ ${\displaystyle \mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),\ldots ]^{T}}$ ${\displaystyle \mu (i)={\frac {1}{1+e^{-\mathbf {w} ^{T}\mathbf {x} (i)}}}}$ ${\displaystyle \mathbf {w} }$

${\displaystyle \mathbf {w} _{k+1}=\left(\mathbf {X} ^{T}\mathbf {S} _{k}\mathbf {X} \right)^{-1}\mathbf {X} ^{T}\left(\mathbf {S} _{k}\mathbf {X} \mathbf {w} _{k}+\mathbf {y} -\mathbf {\boldsymbol {\mu }} _{k}\right)}$

где – диагональная весовая матрица, вектор ожидаемых значений, ${\displaystyle \mathbf {S} =\operatorname {diag} (\mu (i)(1-\mu (i)))}$ ${\displaystyle {\boldsymbol {\mu }}=[\mu (1),\mu (2),\ldots ]}$

${\displaystyle \mathbf {X} ={\begin{bmatrix}1&x_{1}(1)&x_{2}(1)&\ldots \\1&x_{1}(2)&x_{2}(2)&\ldots \\\vdots &\vdots &\vdots \end{bmatrix}}}$

Матрица регрессора и вектор переменных отклика. Более подробную информацию можно найти в литературе. ^[28] ${\displaystyle \mathbf {y} (i)=[y(1),y(2),\ldots ]^{T}}$

Байесовский

Сравнение логистической функции с масштабированной обратной пробит-функцией (т.е. CDF нормального распределения ), сравнение с , что делает наклоны одинаковыми в начале координат. Это показывает более тяжелые хвосты логистического распределения. ${\displaystyle \sigma (x)}$ ${\textstyle \Phi ({\sqrt {\frac {\pi }{8}}}x)}$

В контексте байесовской статистики априорные распределения обычно помещаются в коэффициенты регрессии, например, в форме распределений Гаусса . В логистической регрессии не существует сопряженной априорной функции правдоподобия . Когда байесовский вывод выполнялся аналитически, это затрудняло вычисление апостериорного распределения , за исключением очень малых размерностей. Однако теперь автоматическое программное обеспечение, такое как OpenBUGS , JAGS , PyMC3 , Stan или Turing.jl , позволяет вычислять эти апостериорные данные с помощью моделирования, поэтому отсутствие сопряжения не является проблемой. Однако, когда размер выборки или количество параметров велики, полное байесовское моделирование может быть медленным, и люди часто используют приближенные методы, такие как вариационные байесовские методы и распространение ожиданий .

«Правило десяти»

Широко используемое практическое правило, « правило одного из десяти », гласит, что модели логистической регрессии дают стабильные значения для объясняющих переменных, если они основаны как минимум на примерно 10 событиях на объясняющую переменную (EPV); где событие обозначает случаи, относящиеся к менее частой категории зависимой переменной. Таким образом, исследование, предназначенное для использования объясняющих переменных для события (например, инфаркта миокарда ), которое, как ожидается, произойдет у некоторой части участников исследования, потребует общего числа участников. Однако ведутся серьезные споры о надежности этого правила, которое основано на исследованиях моделирования и не имеет надежного теоретического обоснования. ^[29] По мнению некоторых авторов ^[30] это правило в некоторых обстоятельствах является чрезмерно консервативным, причем авторы заявляют: «Если мы (несколько субъективно) считаем, что охват доверительного интервала составляет менее 93 процентов, ошибка типа I превышает 7 процентов или относительная Если систематическая погрешность превышает 15 процентов как проблемная, наши результаты показывают, что проблемы довольно часты при EPV 2–4, редко встречаются при EPV 5–9 и все еще наблюдаются при EPV 10–16. Наихудшие случаи каждой проблемы не были серьезными при EPV 5–16. 9 EPV и обычно сравнимо с теми, у которых EPV 10–16". ^[31] ${\displaystyle k}$ ${\displaystyle p}$ ${\displaystyle 10k/p}$

Другие нашли результаты, которые не соответствуют вышеизложенному, используя другие критерии. Полезным критерием является то, можно ли ожидать, что подобранная модель достигнет той же прогностической дискриминации в новой выборке, которую она, как оказалось, достигла в выборке для разработки модели. Для этого критерия может потребоваться 20 событий на каждую переменную-кандидата. ^[32] Кроме того, можно утверждать, что 96 наблюдений необходимы только для того, чтобы оценить точку пересечения модели достаточно точно, чтобы погрешность прогнозируемых вероятностей составляла ± 0,1 с уровнем достоверности 0,95. ^[13]

Ошибка и значение соответствия

Тест на отклонение и отношение правдоподобия ─ простой случай

В любой процедуре подбора добавление в модель другого параметра подбора (например, бета-параметров в модели логистической регрессии) почти всегда улучшает способность модели прогнозировать измеренные результаты. Это будет верно, даже если дополнительный член не имеет прогностической ценности, поскольку модель просто будет « подстраиваться » под шум в данных. Возникает вопрос, является ли улучшение, полученное за счет добавления другого подходящего параметра, достаточно значительным, чтобы рекомендовать включение дополнительного термина, или же улучшение является просто тем, которого можно ожидать от переобучения.

Короче говоря, для логистической регрессии определяется статистика, известная как отклонение , которая является мерой ошибки между подгонкой логистической модели и данными результатов. В пределах большого количества точек данных отклонение распределяется по хи-квадрату , что позволяет реализовать критерий хи-квадрат для определения значимости объясняющих переменных.

Линейная регрессия и логистическая регрессия имеют много общего. Например, в простой линейной регрессии набор K точек данных ( x _k , y _k ) соответствует предложенной модельной функции формы . Подбор достигается путем выбора параметров b , которые минимизируют сумму квадратов остатков (квадрат ошибки) для каждой точки данных: ${\displaystyle y=b_{0}+b_{1}x}$

${\displaystyle \epsilon ^{2}=\sum _{k=1}^{K}(b_{0}+b_{1}x_{k}-y_{k})^{2}.}$

Минимальное значение, составляющее соответствие, будет обозначаться ${\displaystyle {\hat {\epsilon }}^{2}}$

Можно ввести идею нулевой модели , в которой предполагается, что переменная x бесполезна для прогнозирования результатов y _k : Точки данных подгоняются к функции нулевой модели формы y=b ₀ с квадратом термин ошибки:

${\displaystyle \epsilon ^{2}=\sum _{k=1}^{K}(b_{0}-y_{k})^{2}.}$

Процесс подгонки состоит из выбора значения b ₀ , которое минимизирует подгонку к нулевой модели, что обозначается знаком, где нижний индекс обозначает нулевую модель. Видно, что нулевая модель оптимизирована по тому, где — среднее значение y _k , а оптимизированная : ${\displaystyle \epsilon ^{2}}$ ${\displaystyle \epsilon _{\varphi }^{2}}$ ${\displaystyle \varphi }$ ${\displaystyle b_{0}={\overline {y}}}$ ${\displaystyle {\overline {y}}}$ ${\displaystyle \epsilon _{\varphi }^{2}}$

${\displaystyle {\hat {\epsilon }}_{\varphi }^{2}=\sum _{k=1}^{K}({\overline {y}}-y_{k})^{2}}$

который пропорционален квадрату (нескорректированного) выборочного стандартного отклонения точек данных y _k .

Мы можем представить себе случай, когда точки данных y _k случайным образом присваиваются различным x _k , а затем подбираются с использованием предложенной модели. _{В частности, мы можем} рассмотреть соответствие предложенной модели каждой перестановке результатов yk . Можно показать, что оптимизированная ошибка любой из этих подгонок никогда не будет меньше оптимальной ошибки нулевой модели, и что разница между этими минимальными ошибками будет подчиняться распределению хи-квадрат со степенями свободы, равными степеням свободы модели. предлагаемой модели минус значения нулевой модели, которые в данном случае будут равны . Используя тест хи-квадрат , мы можем затем оценить, сколько из этих перестановочных наборов y _k дадут минимальную ошибку, меньшую или равную минимальной ошибке, используя исходный y _k , и таким образом мы можем оценить, насколько существенное улучшение дается. путем включения переменной x в предлагаемую модель. ${\displaystyle 2-1=1}$

Для логистической регрессии мерой согласия является функция правдоподобия L или ее логарифм, логарифмическое правдоподобие ℓ . Функция правдоподобия L аналогична функции в случае линейной регрессии, за исключением того, что правдоподобие максимизируется, а не минимизируется. Обозначим максимальное логарифмическое правдоподобие предлагаемой модели через . ${\displaystyle \epsilon ^{2}}$ ${\displaystyle {\hat {\ell }}}$

В случае простой бинарной логистической регрессии набор K точек данных в вероятностном смысле подгоняется к функции вида:

${\displaystyle p(x)={\frac {1}{1+e^{-t}}}}$

где вероятность того, что . Логарифмические шансы определяются следующим образом: ${\displaystyle p(x)}$ ${\displaystyle y=1}$

${\displaystyle t=\beta _{0}+\beta _{1}x}$

и логарифмическая вероятность равна:

${\displaystyle \ell =\sum _{k=1}^{K}\left(y_{k}\ln(p(x_{k}))+(1-y_{k})\ln(1-p(x_{k}))\right)}$

Для нулевой модели вероятность определяется выражением: ${\displaystyle y=1}$

${\displaystyle p_{\varphi }(x)={\frac {1}{1+e^{-t_{\varphi }}}}}$

Логарифмические шансы для нулевой модели определяются следующим образом:

${\displaystyle t_{\varphi }=\beta _{0}}$

и логарифмическая вероятность равна:

${\displaystyle \ell _{\varphi }=\sum _{k=1}^{K}\left(y_{k}\ln(p_{\varphi })+(1-y_{k})\ln(1-p_{\varphi })\right)}$

Поскольку мы имеем максимум L , максимальное логарифмическое правдоподобие для нулевой модели равно ${\displaystyle p_{\varphi }={\overline {y}}}$

${\displaystyle {\hat {\ell }}_{\varphi }=K(\,{\overline {y}}\ln({\overline {y}})+(1-{\overline {y}})\ln(1-{\overline {y}}))}$

Оптимум : ${\displaystyle \beta _{0}}$

${\displaystyle \beta _{0}=\ln \left({\frac {\overline {y}}{1-{\overline {y}}}}\right)}$

где снова среднее значение y _k . Опять же, мы можем концептуально рассмотреть соответствие предлагаемой модели каждой перестановке y k _и можно показать, что максимальная логарифмическая вероятность этих подгонок перестановок никогда не будет меньше, чем у нулевой модели: ${\displaystyle {\overline {y}}}$

${\displaystyle {\hat {\ell }}\geq {\hat {\ell }}_{\varphi }}$

Кроме того, как аналог ошибки в случае линейной регрессии, мы можем определить отклонение подгонки логистической регрессии как:

${\displaystyle D=\ln \left({\frac {{\hat {L}}^{2}}{{\hat {L}}_{\varphi }^{2}}}\right)=2({\hat {\ell }}-{\hat {\ell }}_{\varphi })}$

который всегда будет положительным или нулевым. Причина такого выбора заключается в том, что отклонение не только является хорошей мерой степени соответствия, но также имеет приблизительное распределение хи-квадрат, причем аппроксимация улучшается по мере увеличения числа точек данных ( K ), становясь в точности хи-квадратом. распределены в пределах бесконечного числа точек данных. Как и в случае линейной регрессии, мы можем использовать этот факт для оценки вероятности того, что случайный набор точек данных даст лучшее соответствие, чем соответствие, полученное с помощью предложенной модели, и, таким образом, оценить, насколько значительно модель улучшится за счет включая точки данных x _k в предлагаемой модели.

Для простой модели результатов тестов учащихся, описанной выше, максимальное значение логарифмического правдоподобия нулевой модели равно. Максимальное значение логарифмического правдоподобия для простой модели такое, что отклонение равно ${\displaystyle {\hat {\ell }}_{\varphi }=-13.8629...}$ ${\displaystyle {\hat {\ell }}=-8.02988...}$ ${\displaystyle D=2({\hat {\ell }}-{\hat {\ell }}_{\varphi })=11.6661...}$

Используя критерий значимости хи-квадрат , интеграл распределения хи-квадрат с одной степенью свободы от 11,6661... до бесконечности равен 0,00063649...

Фактически это означает, что можно ожидать, что около 6 из 10 000 подгонок случайного y _k будут иметь лучшее соответствие (меньшее отклонение), чем заданный y _k , и поэтому мы можем заключить, что включение переменной x и данных в предлагаемую модель это очень значительное улучшение по сравнению с нулевой моделью. Другими словами, мы с уверенностью отвергаем нулевую гипотезу . ${\displaystyle 1-D\approx 99.94\%}$

Краткое описание соответствия

Степень соответствия в моделях линейной регрессии обычно измеряется с помощью R 2 . Поскольку это не имеет прямого аналога в логистической регрессии, вместо этого можно использовать различные методы ^{[33] : глава 21,} включая следующие.

Тесты на отклонение и отношение правдоподобия

В анализе линейной регрессии речь идет о разделении дисперсии посредством вычислений суммы квадратов - дисперсия критерия по существу делится на дисперсию, учитываемую предикторами, и остаточную дисперсию. В логистическом регрессионном анализе отклонение используется вместо вычислений суммы квадратов. ^[34] Отклонение аналогично расчетам суммы квадратов в линейной регрессии ^[2] и является мерой несоответствия данным в модели логистической регрессии. ^[34] Когда доступна «насыщенная» модель (модель с теоретически идеальным соответствием), отклонение рассчитывается путем сравнения данной модели с насыщенной моделью. ^[2] Это вычисление дает тест отношения правдоподобия : ^[2]

${\displaystyle D=-2\ln {\frac {\text{likelihood of the fitted model}}{\text{likelihood of the saturated model}}}.}$

В приведенном выше уравнении D представляет отклонение, а ln представляет натуральный логарифм. Логарифм этого отношения правдоподобия (отношение подобранной модели к насыщенной модели) даст отрицательное значение, следовательно, необходим отрицательный знак. Можно показать, что D соответствует приблизительному распределению хи-квадрат . ^[2] Меньшие значения указывают на лучшее соответствие, поскольку подобранная модель меньше отклоняется от насыщенной модели. При оценке по распределению хи-квадрат незначительные значения хи-квадрат указывают на очень небольшую необъяснимую дисперсию и, следовательно, на хорошее соответствие модели. И наоборот, значительное значение хи-квадрат указывает на то, что значительная часть дисперсии необъяснима.

Когда насыщенная модель недоступна (обычный случай), отклонение рассчитывается просто как -2 · (логарифм правдоподобия подобранной модели), и ссылку на логарифм правдоподобия насыщенной модели можно без вреда удалить из всего, что следует дальше.

В логистической регрессии особенно важны две меры отклонения: нулевое отклонение и отклонение модели. Нулевое отклонение представляет собой разницу между моделью только с точкой пересечения (что означает «нет предикторов») и насыщенной моделью. Отклонение модели представляет собой разницу между моделью хотя бы с одним предиктором и насыщенной моделью. ^[34] В этом отношении нулевая модель обеспечивает основу для сравнения моделей предикторов. Учитывая, что отклонение является мерой различия между данной моделью и насыщенной моделью, меньшие значения указывают на лучшее соответствие. Таким образом, для оценки вклада предиктора или набора предикторов можно вычесть отклонение модели из нулевого отклонения и оценить разницу на распределении хи-квадрат со степенями свободы ^[2] , равным разнице числа параметров оцененный. ${\displaystyle \chi _{s-p}^{2},}$

Позволять

${\displaystyle {\begin{aligned}D_{\text{null}}&=-2\ln {\frac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}\\[6pt]D_{\text{fitted}}&=-2\ln {\frac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}.\end{aligned}}}$

Тогда разница обоих:

${\displaystyle {\begin{aligned}D_{\text{null}}-D_{\text{fitted}}&=-2\left(\ln {\frac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}-\ln {\frac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}\right)\\[6pt]&=-2\ln {\frac {\left({\dfrac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}\right)}{\left({\dfrac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}\right)}}\\[6pt]&=-2\ln {\frac {\text{likelihood of the null model}}{\text{likelihood of fitted model}}}.\end{aligned}}}$

Если отклонение модели значительно меньше, чем нулевое отклонение, можно сделать вывод, что предиктор или набор предикторов значительно улучшают соответствие модели. Это аналогично F -тесту, используемому в анализе линейной регрессии для оценки значимости прогноза. ^[34]

Псевдо-R-квадрат

В линейной регрессии квадратичная множественная корреляция R ² используется для оценки степени соответствия, поскольку она представляет собой долю дисперсии критерия, объясняемую предикторами. ^[34] В логистическом регрессионном анализе не существует согласованной аналогичной меры, но существует несколько конкурирующих мер, каждая из которых имеет ограничения. ^{[34] [35]}

На этой странице рассмотрены четыре наиболее часто используемых индекса и один менее распространенный:

• Отношение правдоподобия R ² _L
• Кокс и Снелл R ² _CS
• Нагелькерке Р ² _Н
• Макфадден Р ² _МакФ
• Тьюр Р ² _Т

Тест Хосмера – Лемешоу

Тест Хосмера -Лемешоу использует тестовую статистику, которая асимптотически следует распределению , чтобы оценить, соответствуют ли наблюдаемые частоты событий ожидаемым частотам событий в подгруппах модельной совокупности. Некоторые статистики считают этот тест устаревшим из-за его зависимости от произвольного группирования прогнозируемых вероятностей и относительно низкой мощности. ^[36] ${\displaystyle \chi ^{2}}$

Значимость коэффициента

После подбора модели исследователи, вероятно, захотят изучить вклад отдельных предикторов. Для этого они захотят изучить коэффициенты регрессии. В линейной регрессии коэффициенты регрессии представляют собой изменение критерия для каждого изменения единицы предиктора. ^[34] Однако в логистической регрессии коэффициенты регрессии представляют собой изменение логита для каждого изменения единицы предиктора. Учитывая, что логит не является интуитивно понятным, исследователи, вероятно, сосредоточат внимание на влиянии предиктора на экспоненциальную функцию коэффициента регрессии – отношение шансов (см. определение). В линейной регрессии значимость коэффициента регрессии оценивается путем вычисления t- критерия. В логистической регрессии существует несколько различных тестов, предназначенных для оценки значимости отдельного предиктора, в первую очередь тест отношения правдоподобия и статистика Вальда.

Тест отношения правдоподобия

Обсужденный выше тест отношения правдоподобия для оценки соответствия модели также является рекомендуемой процедурой для оценки вклада отдельных «предсказателей» в данную модель. ^{[2] [25] [34]} В случае одной модели предиктора просто сравнивают отклонение модели предиктора с отклонением нулевой модели на распределении хи-квадрат с одной степенью свободы. Если модель предиктора имеет значительно меньшее отклонение (ср. хи-квадрат, использующий разницу в степенях свободы двух моделей), то можно заключить, что существует значительная связь между «предсказателем» и результатом. Хотя некоторые распространенные статистические пакеты (например, SPSS) предоставляют статистику теста отношения правдоподобия, без этого трудоемкого теста было бы сложнее оценить вклад отдельных предикторов в случае множественной логистической регрессии. ^{[ нужна цитата ]} Чтобы оценить вклад отдельных предикторов, можно ввести предикторы иерархически, сравнивая каждую новую модель с предыдущей, чтобы определить вклад каждого предиктора. ^[34] Среди статистиков ведутся споры о целесообразности так называемых «пошаговых» процедур. ^{[ ласковые слова ]} Есть опасение, что они могут не сохранить номинальные статистические свойства и могут ввести в заблуждение. ^[37]

Статистика Вальда

Альтернативно, при оценке вклада отдельных предикторов в данной модели можно проверить значимость статистики Вальда . Статистика Вальда, аналогичная t -критерию в линейной регрессии, используется для оценки значимости коэффициентов. Статистика Вальда представляет собой отношение квадрата коэффициента регрессии к квадрату стандартной ошибки коэффициента и асимптотически распределяется как распределение хи-квадрат. ^[25]

${\displaystyle W_{j}={\frac {\beta _{j}^{2}}{SE_{\beta _{j}}^{2}}}}$

Хотя некоторые статистические пакеты (например, SPSS, SAS) предоставляют статистику Вальда для оценки вклада отдельных предикторов, статистика Вальда имеет ограничения. Когда коэффициент регрессии велик, стандартная ошибка коэффициента регрессии также имеет тенденцию быть больше, увеличивая вероятность ошибки второго рода . Статистика Уолда также имеет тенденцию быть необъективной, когда данных мало. ^[34]

Выборка случай-контроль

Предположим, случаи редки. Тогда мы могли бы захотеть проверять их чаще, чем их распространенность среди населения. Например, предположим, что есть заболевание, которым страдает 1 человек из 10 000, и для сбора данных нам необходимо пройти полный медицинский осмотр. Проводить тысячи медосмотров здоровых людей, чтобы получить данные лишь о нескольких больных, может быть слишком дорого. Таким образом, мы можем оценить больше больных людей, возможно, все редкие исходы. Это также ретроспективная выборка или, что то же самое, называется несбалансированными данными. Как правило, контрольная выборка в количестве, в пять раз превышающем количество случаев, дает достаточные контрольные данные. ^[38]

Логистическая регрессия уникальна тем, что ее можно оценить на основе несбалансированных данных, а не на случайно выбранных данных, и при этом она дает правильные оценки коэффициентов влияния каждой независимой переменной на результат. То есть, если мы формируем логистическую модель на основе таких данных, если модель верна для генеральной совокупности, все параметры верны, за исключением . Мы можем исправить это , если знаем истинную распространенность следующим образом: ^[38] ${\displaystyle \beta _{j}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$

${\displaystyle {\widehat {\beta }}_{0}^{*}={\widehat {\beta }}_{0}+\log {\frac {\pi }{1-\pi }}-\log {{\tilde {\pi }} \over {1-{\tilde {\pi }}}}}$

где – истинная распространенность и – распространенность в выборке. ${\displaystyle \pi }$ ${\displaystyle {\tilde {\pi }}}$

Обсуждение

Как и другие формы регрессионного анализа , логистическая регрессия использует одну или несколько переменных-предикторов, которые могут быть непрерывными или категориальными. Однако, в отличие от обычной линейной регрессии, логистическая регрессия используется для прогнозирования зависимых переменных, которые относятся к одной из ограниченного числа категорий (в биномиальном случае зависимая переменная рассматривается как результат испытания Бернулли ), а не для непрерывного результата. Учитывая эту разницу, предположения линейной регрессии нарушаются. В частности, остатки не могут быть нормально распределены. Кроме того, линейная регрессия может давать бессмысленные прогнозы для бинарной зависимой переменной. Необходим способ преобразования двоичной переменной в непрерывную, которая может принимать любое действительное значение (отрицательное или положительное). Для этого биномиальная логистическая регрессия сначала вычисляет вероятность того, что событие произойдет для разных уровней каждой независимой переменной, а затем логарифмирует ее, чтобы создать непрерывный критерий как преобразованную версию зависимой переменной. Логарифм шансов – это логит вероятности, логит определяется следующим образом:

$${\displaystyle \operatorname {logit} p=\ln {\frac {p}{1-p}}\quad {\text{for }}0<p<1\,.}$$

Хотя зависимой переменной в логистической регрессии является Бернулли, логит имеет неограниченный масштаб. ^[2] Логит-функция — это функция связи в такой обобщенной линейной модели, т.е.

$${\displaystyle \operatorname {logit} \operatorname {\mathcal {E}} (Y)=\beta _{0}+\beta _{1}x}$$

Y — переменная отклика, распределенная по Бернулли, а x — предикторная переменная; значения β являются линейными параметрами.

Затем логит вероятности успеха подгоняется под предикторы. Прогнозируемое значение логита преобразуется обратно в прогнозируемые шансы посредством обратной функции натурального логарифма – экспоненциальной функции . Таким образом, хотя наблюдаемая зависимая переменная в бинарной логистической регрессии представляет собой переменную 0 или 1, логистическая регрессия как непрерывная переменная оценивает вероятность того, что зависимая переменная является «успехом». В некоторых приложениях достаточно только шансов. В других случаях необходим конкретный прогноз «да» или «нет» для определения того, является ли зависимая переменная «успехом» или нет; этот категориальный прогноз может быть основан на вычисленных шансах на успех, при этом прогнозируемые шансы выше некоторого выбранного порогового значения преобразуются в прогноз успеха.

Максимальная энтропия

Из всех функциональных форм, используемых для оценки вероятностей конкретного категориального результата, которые оптимизируют соответствие путем максимизации функции правдоподобия (например, пробит-регрессия , регрессия Пуассона и т. д.), решение логистической регрессии является уникальным, поскольку оно является решением с максимальной энтропией . . ^[39] Это случай общего свойства: экспоненциальное семейство распределений максимизирует энтропию при заданном ожидаемом значении. В случае логистической модели логистическая функция является естественным параметром распределения Бернулли (она находится в « канонической форме », а логистическая функция — это каноническая функция связи), тогда как другие сигмовидные функции являются неканоническими функциями связи; это лежит в основе его математической элегантности и простоты оптимизации. Подробности см. в разделе Экспоненциальное семейство § Вывод максимальной энтропии .

Доказательство

Чтобы это показать, воспользуемся методом множителей Лагранжа . Лагранжиан равен энтропии плюс сумме произведений множителей Лагранжа на различные выражения ограничений. Будет рассмотрен общий полиномиальный случай, поскольку рассмотрение более простых случаев не сильно упрощает доказательство. Приравнивание производной лагранжиана по различным вероятностям нулю дает функциональную форму для этих вероятностей, которая соответствует формам, используемым в логистической регрессии. ^[39]

Как и в приведенном выше разделе о полиномиальной логистической регрессии, мы будем рассматривать объясняющие переменные, обозначенные и которые включают . Всего будет K точек данных, проиндексированных , а точки данных обозначаются и . x _mk также будет представлен как -мерный вектор . Возможные значения категориальной переменной y будут варьироваться от 0 до N. ${\displaystyle M+1}$ ${\displaystyle x_{m}}$ ${\displaystyle x_{0}=1}$ ${\displaystyle k=\{1,2,\dots ,K\}}$ ${\displaystyle x_{mk}}$ ${\displaystyle y_{k}}$ ${\displaystyle (M+1)}$ ${\displaystyle {\boldsymbol {x}}_{k}=\{x_{0k},x_{1k},\dots ,x_{Mk}\}}$ ${\displaystyle N+1}$

Пусть p _n ( x ) будет вероятностью при данном векторе объясняющей переменной x того, что результат будет . Определите, какова вероятность того, что для k -го измерения категориальный результат равен n . ${\displaystyle y=n}$ ${\displaystyle p_{nk}=p_{n}({\boldsymbol {x}}_{k})}$

Лагранжиан будет выражаться как функция вероятностей p _nk и минимизироваться путем приравнивания производных лагранжиана по этим вероятностям нулю. Важным моментом является то, что вероятности рассматриваются одинаково, и тот факт, что их сумма равна 1, является частью лагранжевой формулировки, а не предполагается с самого начала.

Первым вкладом в лагранжиан является энтропия :

${\displaystyle {\mathcal {L}}_{ent}=-\sum _{k=1}^{K}\sum _{n=0}^{N}p_{nk}\ln(p_{nk})}$

Логарифмическая вероятность равна:

${\displaystyle \ell =\sum _{k=1}^{K}\sum _{n=0}^{N}\Delta (n,y_{k})\ln(p_{nk})}$

Предполагая полиномиальную логистическую функцию, производная логарифмического правдоподобия по бета-коэффициентам оказалась равной:

${\displaystyle {\frac {\partial \ell }{\partial \beta _{nm}}}=\sum _{k=1}^{K}(p_{nk}x_{mk}-\Delta (n,y_{k})x_{mk})}$

Очень важным моментом здесь является то, что это выражение (что примечательно) не является явной функцией бета-коэффициентов. Это всего лишь функция вероятностей pnk и данных _. Вместо того, чтобы быть специфичным для предполагаемого полиномиального логистического случая, оно считается общим утверждением условия, при котором логарифмическое правдоподобие максимизируется, и не делает ссылки на функциональную форму p _nk . Тогда существуют ( M +1)( N +1) ограничения аппроксимации, и член ограничения аппроксимации в лагранжиане тогда равен:

${\displaystyle {\mathcal {L}}_{fit}=\sum _{n=0}^{N}\sum _{m=0}^{M}\lambda _{nm}\sum _{k=1}^{K}(p_{nk}x_{mk}-\Delta (n,y_{k})x_{mk})}$

где λ _нм — соответствующие множители Лагранжа. Существует K ограничений нормализации, которые можно записать:

${\displaystyle \sum _{n=0}^{N}p_{nk}=1}$

так что нормировочный член в лагранжиане равен:

${\displaystyle {\mathcal {L}}_{norm}=\sum _{k=1}^{K}\alpha _{k}\left(1-\sum _{n=1}^{N}p_{nk}\right)}$

где α _k — соответствующие множители Лагранжа. Тогда лагранжиан представляет собой сумму трех вышеуказанных членов:

${\displaystyle {\mathcal {L}}={\mathcal {L}}_{ent}+{\mathcal {L}}_{fit}+{\mathcal {L}}_{norm}}$

Приравнивание производной лагранжиана по одной из вероятностей к нулю дает:

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial p_{n'k'}}}=0=-\ln(p_{n'k'})-1+\sum _{m=0}^{M}(\lambda _{n'm}x_{mk'})-\alpha _{k'}}$

Используя более сжатую векторную запись:

${\displaystyle \sum _{m=0}^{M}\lambda _{nm}x_{mk}={\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}$

и отбрасываем простые числа от индексов n и k , а затем находим доходность : ${\displaystyle p_{nk}}$

${\displaystyle p_{nk}=e^{{\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}/Z_{k}}$

где:

${\displaystyle Z_{k}=e^{1+\alpha _{k}}}$

Наложив ограничение нормализации, мы можем найти Z _k и записать вероятности как:

${\displaystyle p_{nk}={\frac {e^{{\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}}{\sum _{u=0}^{N}e^{{\boldsymbol {\lambda }}_{u}\cdot {\boldsymbol {x}}_{k}}}}}$

Не все они независимы. Мы можем добавить любой постоянный размерный вектор к каждому из них, не меняя значения вероятностей, так что будет только N , а не независимых . В приведенном выше разделе полиномиальной логистической регрессии из каждого была вычтена величина, устанавливающая экспоненциальный член, включающий значение 1, а бета-коэффициенты были заданы как . ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle (M+1)}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle p_{nk}}$ ${\displaystyle N+1}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle {\boldsymbol {\lambda }}_{0}}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle {\boldsymbol {\lambda }}_{0}}$ ${\displaystyle {\boldsymbol {\beta }}_{n}={\boldsymbol {\lambda }}_{n}-{\boldsymbol {\lambda }}_{0}}$

Другие подходы

В приложениях машинного обучения, где для двоичной классификации используется логистическая регрессия, MLE минимизирует функцию перекрестных энтропийных потерь.

Логистическая регрессия — важный алгоритм машинного обучения . Цель состоит в том, чтобы смоделировать вероятность того, что случайная величина будет равна 0 или 1 с учетом экспериментальных данных. ^[40] ${\displaystyle Y}$

Рассмотрим обобщенную линейную модельную функцию, параметризованную , ${\displaystyle \theta }$

${\displaystyle h_{\theta }(X)={\frac {1}{1+e^{-\theta ^{T}X}}}=\Pr(Y=1\mid X;\theta )}$

Поэтому,

${\displaystyle \Pr(Y=0\mid X;\theta )=1-h_{\theta }(X)}$

и поскольку мы видим, что это определяется выражением. Теперь мы вычисляем функцию правдоподобия, предполагая, что все наблюдения в выборке независимо распределены Бернулли, ${\displaystyle Y\in \{0,1\}}$ ${\displaystyle \Pr(y\mid X;\theta )}$ ${\displaystyle \Pr(y\mid X;\theta )=h_{\theta }(X)^{y}(1-h_{\theta }(X))^{(1-y)}.}$

${\displaystyle {\begin{aligned}L(\theta \mid y;x)&=\Pr(Y\mid X;\theta )\\&=\prod _{i}\Pr(y_{i}\mid x_{i};\theta )\\&=\prod _{i}h_{\theta }(x_{i})^{y_{i}}(1-h_{\theta }(x_{i}))^{(1-y_{i})}\end{aligned}}}$

Обычно вероятность журнала максимальна,

${\displaystyle N^{-1}\log L(\theta \mid y;x)=N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i}\mid x_{i};\theta )}$

который максимизируется с помощью методов оптимизации, таких как градиентный спуск .

Предполагая, что пары выбраны равномерно из основного распределения, тогда в пределе больших  N , ${\displaystyle (x,y)}$

${\displaystyle {\begin{aligned}&\lim \limits _{N\rightarrow +\infty }N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i}\mid x_{i};\theta )=\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\Pr(X=x,Y=y)\log \Pr(Y=y\mid X=x;\theta )\\[6pt]={}&\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\Pr(X=x,Y=y)\left(-\log {\frac {\Pr(Y=y\mid X=x)}{\Pr(Y=y\mid X=x;\theta )}}+\log \Pr(Y=y\mid X=x)\right)\\[6pt]={}&-D_{\text{KL}}(Y\parallel Y_{\theta })-H(Y\mid X)\end{aligned}}}$

где – условная энтропия , – расходимость Кульбака–Лейблера . Это приводит к интуитивному пониманию того, что, максимизируя логарифмическое правдоподобие модели, вы минимизируете отклонение KL вашей модели от максимального распределения энтропии. Интуитивный поиск модели, которая делает наименьшее количество допущений в своих параметрах. ${\displaystyle H(Y\mid X)}$ ${\displaystyle D_{\text{KL}}}$

Сравнение с линейной регрессией

Логистическую регрессию можно рассматривать как частный случай обобщенной линейной модели и, таким образом, аналог линейной регрессии . Однако модель логистической регрессии основана на совершенно иных предположениях (о взаимосвязи между зависимыми и независимыми переменными), чем в линейной регрессии. В частности, ключевые различия между этими двумя моделями можно увидеть в следующих двух особенностях логистической регрессии. Во-первых, условное распределение представляет собой распределение Бернулли, а не распределение Гаусса , поскольку зависимая переменная является двоичной. Во-вторых, прогнозируемые значения являются вероятностями и поэтому ограничены значением (0,1) посредством функции логистического распределения , поскольку логистическая регрессия предсказывает вероятность конкретных результатов, а не сами результаты. ${\displaystyle y\mid x}$

Альтернативы

Распространенной альтернативой логистической модели (логит-модели) является пробит-модель , как следует из родственных названий. С точки зрения обобщенных линейных моделей они различаются выбором функции связи : логистическая модель использует логит-функцию (обратную логистическую функцию), а пробит-модель использует пробит-функцию (обратную функцию ошибок ). Аналогично, в интерпретации скрытых переменных этих двух методов первый предполагает стандартное логистическое распределение ошибок, а второй - стандартное нормальное распределение ошибок. ^[41] Вместо этого можно использовать другие сигмовидные функции или распределения ошибок.

Логистическая регрессия является альтернативой методу Фишера 1936 года — линейному дискриминантному анализу . ^[42] Если предположения линейного дискриминантного анализа верны, условие можно изменить на противоположное, чтобы получить логистическую регрессию. Однако обратное неверно, поскольку логистическая регрессия не требует многомерного нормального предположения дискриминантного анализа. ^[43]

Предположение о линейных эффектах прогнозирования можно легко ослабить, используя такие методы, как сплайн-функции . ^[13]

История

Подробная история логистической регрессии представлена ​​у Крамера (2002). Логистическая функция была разработана как модель роста населения и названа «логистикой» Пьером Франсуа Верхюльстом в 1830-х и 1840-х годах под руководством Адольфа Кетле ; подробности см. в разделе Логистическая функция § История . ^[44] В своей самой ранней статье (1838 г.) Ферхюльст не уточнил, как он согласовал кривые с данными. ^{[45] [46]} В своей более подробной статье (1845 г.) Ферхюльст определил три параметра модели, заставив кривую проходить через три наблюдаемые точки, что дало плохие прогнозы. ^{[47] [48]}

Логистическая функция была независимо разработана в химии как модель автокатализа ( Вильгельм Оствальд , 1883). ^[49] Автокаталитическая реакция — это реакция, в которой один из продуктов сам является катализатором той же реакции, в то время как запас одного из реагентов фиксирован. Это естественным образом приводит к логистическому уравнению по той же причине, что и рост населения: реакция является самоусиливающейся, но ограниченной.

Логистическая функция была независимо заново открыта как модель роста населения в 1920 году Рэймондом Перлом и Лоуэллом Ридом и опубликована как Pearl & Reed (1920), что привело к ее использованию в современной статистике. Первоначально они не знали о работе Ферхюльста и, по-видимому, узнали о ней от Л. Гюстава дю Паскье , но мало доверяли ему и не переняли его терминологию. ^[50] Приоритет Ферхюльста был признан, а термин «логистика» возрожден Удным Юлом в 1925 году и используется с тех пор. ^[51] Перл и Рид сначала применили модель к населению Соединенных Штатов, а также первоначально подогнали кривую, заставив ее проходить через три точки; как и в случае с Верхюльстом, это снова дало плохие результаты. ^[52]

В 1930-х годах пробит-модель была разработана и систематизирована Честером Иттнером Блиссом , который ввел термин «пробит» в «Блиссе» (1934), и Джоном Гаддумом в «Гаддуме» (1933), а модель соответствовала оценке максимального правдоподобия Рональда А. Фишер в «Фишере» (1935), как дополнение к работе Блисс. Модель пробита в основном использовалась в биоанализе , и ей предшествовали более ранние работы, датированные 1860 годом; см. Модель Пробита § История . Модель пробит повлияла на последующее развитие модели логит, и эти модели конкурировали друг с другом. ^[53]

Логистическая модель, вероятно, была впервые использована в качестве альтернативы пробит-модели в биоанализе Эдвином Бидуэллом Уилсоном и его студенткой Джейн Вустер в работе Wilson & Worcester (1943). ^[54] Однако развитие логистической модели как общей альтернативы пробит-модели произошло главным образом благодаря работе Джозефа Берксона на протяжении многих десятилетий, начиная с Берксона (1944), где он ввел термин «логит» по аналогии с «логитом». пробит», и продолжился в Берксоне (1951) и в последующие годы. ^[55] Логит-модель изначально считалась уступающей пробит-модели, но «постепенно достигла равного положения с логит-моделью», ^[56], особенно между 1960 и 1970 годами. К 1970 году логит-модель достигла паритета с пробит-моделью в использовать в статистических журналах и впоследствии превзошел его. Эта относительная популярность была обусловлена ​​​​принятием логита за пределами биоанализа, а не вытеснением пробита в биоанализе и его неофициальным использованием на практике; Популярность логита объясняется вычислительной простотой, математическими свойствами и общностью модели логита, что позволяет использовать ее в различных областях. ^[3]

За это время произошли различные усовершенствования, в частности Дэвидом Коксом , как в работе Кокса (1958). ^[4]

Полиномиальная логит-модель была независимо представлена ​​Коксом (1966) и Тейлом (1969), что значительно расширило сферу применения и популярность логит-модели. ^[57] В 1973 году Дэниел Макфадден связал полиномиальный логит с теорией дискретного выбора , в частности с аксиомой выбора Люса , показав, что полиномиальный логит следует из предположения о независимости нерелевантных альтернатив и интерпретации шансов альтернатив как относительных предпочтений; ^[58] это дало теоретическую основу для логистической регрессии. ^[57]

Расширения

Существует большое количество расширений:

• Полиномиальная логистическая регрессия (или полиномиальный логит ) обрабатывает случай многофакторной категориальной зависимой переменной (с неупорядоченными значениями, также называемыми «классификацией»). Общий случай наличия зависимых переменных с более чем двумя значениями называется политомической регрессией .
• Упорядоченная логистическая регрессия (или упорядоченная логистика ) обрабатывает порядковые зависимые переменные (упорядоченные значения).
• Смешанный логит — это расширение полиномиального логита, которое учитывает корреляции между выбором зависимой переменной.
• Расширением логистической модели на наборы взаимозависимых переменных является условное случайное поле .
• Условная логистическая регрессия обрабатывает сопоставленные или стратифицированные данные, когда слои небольшие. Чаще всего он используется при анализе наблюдательных исследований .

Смотрите также

• Математический портал

• Логистическая функция
• Дискретный выбор
• Модель Джарроу – Тернбулла
• Ограниченная зависимая переменная
• Полиномиальная логит-модель
• Заказанный логит
• Тест Хосмера – Лемешоу
• Оценка Брайера
• mlpack — содержит реализацию логистической регрессии на C++.
• Местная выборка случай-контроль
• Дерево логистической модели

Рекомендации

1. Толлес, Джулиана; Мёрер, Уильям Дж (2016). «Логистическая регрессия, связывающая характеристики пациента с результатами». ДЖАМА . 316 (5): 533–4. дои : 10.1001/jama.2016.7653. ISSN  0098-7484. OCLC  6823603312. PMID  27483067.
2. Хосмер, Дэвид В.; Лемешоу, Стэнли (2000). Прикладная логистическая регрессия (2-е изд.). Уайли. ISBN 978-0-471-35632-5.^{[ нужна страница ]}
3. Крамер 2002, с. 10–11.
4. Уокер, SH; Дункан, Д.Б. (1967). «Оценка вероятности события как функция нескольких независимых переменных». Биометрика . 54 (1/2): 167–178. дои : 10.2307/2333860. JSTOR  2333860.
5. Крамер 2002, с. 8.
6. Бойд, CR; Толсон, Массачусетс; Коупс, WS (1987). «Оценка помощи при травмах: метод TRISS. Оценка травмы и оценка тяжести травмы». Журнал травмы . 27 (4): 370–378. дои : 10.1097/00005373-198704000-00005 . ПМИД  3106646.
7. Кологлу, М.; Элкер, Д.; Алтун, Х.; Саек, И. (2001). «Валидация MPI и PIA II в двух разных группах пациентов с вторичным перитонитом». Гепато-гастроэнтерология . 48 (37): 147–51. ПМИД  11268952.
8. Биондо, С.; Рамос, Э.; Дейрос, М.; Раге, Ж.М.; Де Ока, Дж.; Морено, П.; Фарран, Л.; Джаурриета, Э. (2000). «Прогностические факторы смертности при перитоните левой толстой кишки: новая система оценки». Журнал Американского колледжа хирургов . 191 (6): 635–42. дои : 10.1016/S1072-7515(00)00758-4. ПМИД  11129812.
9. Маршалл, JC; Кук, диджей; Кристу, Невада; Бернар, Греция; Спринг, CL; Сиббальд, WJ (1995). «Показатель множественной дисфункции органов: надежный дескриптор сложного клинического исхода». Медицина критических состояний . 23 (10): 1638–52. дои : 10.1097/00003246-199510000-00007. ПМИД  7587228.
10. Ле Галл, младший; Лемешоу, С.; Солнье, Ф. (1993). «Новая упрощенная оценка острой физиологии (SAPS II), основанная на многоцентровом исследовании Европы и Северной Америки». ДЖАМА . 270 (24): 2957–63. дои : 10.1001/jama.1993.03510240069035. ПМИД  8254858.
11. Дэвид А. Фридман (2009). Статистические модели: теория и практика . Издательство Кембриджского университета . п. 128.
12. Труэтт, Дж; Корнфилд, Дж; Каннел, W (1967). «Многомерный анализ риска ишемической болезни сердца во Фремингеме». Журнал хронических болезней . 20 (7): 511–24. дои : 10.1016/0021-9681(67)90082-3. ПМИД  6028270.
13. Харрелл, Фрэнк Э. (2015). Стратегии регрессионного моделирования . Серия Спрингера по статистике (2-е изд.). Нью-Йорк; Спрингер. дои : 10.1007/978-3-319-19425-7. ISBN 978-3-319-19424-0.
14. М. Страно; Б.М. Колозимо (2006). «Логистический регрессионный анализ для экспериментального определения формирования предельных диаграмм». Международный журнал станков и производства . 46 (6): 673–682. doi :10.1016/j.ijmachtools.2005.07.005.
15. Палей, СК; Дас, СК (2009). «Модель логистической регрессии для прогнозирования рисков падения кровли в бортовых и столбовых выработках угольных шахт: подход». Наука безопасности . 47 : 88–96. doi : 10.1016/j.ssci.2008.01.002.
16. Берри, Майкл Дж. А. (1997). Методы интеллектуального анализа данных для маркетинга, продаж и поддержки клиентов . Уайли. п. 10.
17. Меса-Аранго, Родриго; Хасан, Самиул; Уккусури, Сатиш В.; Мюррей-Туит, Памела (февраль 2013 г.). «Модель на уровне домохозяйства для выбора типа пункта назначения эвакуации при урагане с использованием данных об урагане Иван». Обзор природных опасностей . 14 (1): 11–20. doi : 10.1061/(ASCE)NH.1527-6996.0000083. ISSN  1527-6988.
18. Виббенмейер, Мэтью Дж.; Хэнд, Майкл С.; Калкин, Дэвид Э.; Венн, Тайрон Дж.; Томпсон, Мэтью П. (июнь 2013 г.). «Предпочтения риска при принятии стратегических решений по поводу лесных пожаров: эксперимент по выбору с менеджерами по борьбе с лесными пожарами в США». Анализ риска . 33 (6): 1021–1037. Бибкод : 2013RiskA..33.1021W. дои : 10.1111/j.1539-6924.2012.01894.x. ISSN  0272-4332. PMID  23078036. S2CID  45282555.
19. Ловреглио, Руджеро; Борри, Дино; дель Олио, Луиджи; Ибеас, Ангел (01 февраля 2014 г.). «Модель дискретного выбора, основанная на случайных утилитах для выбора выхода при экстренной эвакуации». Наука безопасности . 62 : 418–426. doi :10.1016/j.ssci.2013.10.004. ISSN  0925-7535.
20. Нейман, Дж .; Пирсон, ES (1933), «О проблеме наиболее эффективных проверок статистических гипотез» (PDF) , Philosophical Transactions of the Royal Society of London A , 231 (694–706): 289–337, Бибкод : 1933RSPTA.231 ..289N, doi : 10.1098/rsta.1933.0009 , JSTOR  91247
21. «Как интерпретировать соотношение шансов в логистической регрессии?». Институт цифровых исследований и образования.
22. Эверитт, Брайан (1998). Кембриджский статистический словарь . Кембридж, Великобритания, Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-59346-5.
23. Например, индикаторную функцию в этом случае можно определить как ${\displaystyle \Delta (n,y)=1-(y-n)^{2}}$
24. Малуф, Роберт (2002). «Сравнение алгоритмов оценки параметров максимальной энтропии». Материалы шестой конференции по изучению естественного языка (CoNLL-2002) . стр. 49–55. дои : 10.3115/1118853.1118871 .
25. Менард, Скотт В. (2002). Прикладная логистическая регрессия (2-е изд.). МУДРЕЦ. ISBN 978-0-7619-2208-7.^{[ нужна страница ]}
26. Гурьеро, Кристиан; Монфор, Ален (1981). «Асимптотические свойства оценки максимального правдоподобия в дихотомических логит-моделях». Журнал эконометрики . 17 (1): 83–97. дои : 10.1016/0304-4076(81)90060-9.
27. Пак, Бён У.; Симар, Леопольд; Зеленюк, Валентин (2017). «Непараметрическая оценка динамических моделей дискретного выбора для данных временных рядов» (PDF) . Вычислительная статистика и анализ данных . 108 : 97–120. дои : 10.1016/j.csda.2016.10.024.
28. Мерфи, Кевин П. (2012). Машинное обучение – вероятностная перспектива . Массачусетский технологический институт Пресс. п. 245. ИСБН 978-0-262-01802-9.
29. Ван Смеден, М.; Де Гроот, Дж.А.; Мунс, КГ; Коллинз, Дж.С.; Альтман, Д.Г.; Эйкеманс, MJ; Рейтсма, Дж.Б. (2016). «Нет обоснования критерия 1 переменная на 10 событий для анализа бинарной логистической регрессии». Методология медицинских исследований BMC . 16 (1): 163. дои : 10.1186/s12874-016-0267-3 . ПМК 5122171 . ПМИД  27881078. 
30. Педуцци, П; Конкато, Дж; Кемпер, Э; Холфорд, TR; Файнштейн, Арканзас (декабрь 1996 г.). «Моделирующее исследование количества событий на переменную в логистическом регрессионном анализе». Журнал клинической эпидемиологии . 49 (12): 1373–9. дои : 10.1016/s0895-4356(96)00236-3 . ПМИД  8970487.
31. Виттингофф, Э.; Маккалок, CE (12 января 2007 г.). «Ослабление правила десяти событий на переменную в логистической регрессии и регрессии Кокса». Американский журнал эпидемиологии . 165 (6): 710–718. дои : 10.1093/aje/kwk052 . ПМИД  17182981.
32. ван дер Плог, Тьерд; Остин, Питер С.; Стейерберг, Эвоут В. (2014). «Современные методы моделирования требуют данных: исследование моделирования для прогнозирования дихотомических конечных точек». Методология медицинских исследований BMC . 14 :137. дои : 10.1186/1471-2288-14-137 . ПМЦ 4289553 . ПМИД  25532820. 
33. Грин, Уильям Н. (2003). Эконометрический анализ (Пятое изд.). Прентис-Холл. ISBN 978-0-13-066189-0.
34. Коэн, Джейкоб; Коэн, Патрисия; Уэст, Стивен Г.; Эйкен, Леона С. (2002). Прикладной множественный регрессионный/корреляционный анализ для поведенческих наук (3-е изд.). Рутледж. ISBN 978-0-8058-2223-6.^{[ нужна страница ]}
35. Эллисон, Пол Д. «Меры соответствия логистической регрессии» (PDF) . Statistical Horizons LLC и Пенсильванский университет.
36. Хосмер, Д.В. (1997). «Сравнение критериев согласия для модели логистической регрессии». Стат Мед . 16 (9): 965–980. doi :10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.3.co;2-f. ПМИД  9160492.
37. Харрелл, Фрэнк Э. (2010). Стратегии регрессионного моделирования: с приложениями к линейным моделям, логистической регрессии и анализу выживания . Нью-Йорк: Спрингер. ISBN 978-1-4419-2918-1.^{[ нужна страница ]}
38. https://class.stanford.edu/c4x/HumanitiesScience/StatLearning/asset/classification.pdf, слайд 16.
39. Маунт, Дж. (2011). «Эквивалентность моделей логистической регрессии и максимальной энтропии» (PDF) . Проверено 23 февраля 2022 г.
40. Нг, Эндрю (2000). «Конспекты лекций CS229» (PDF) . CS229 Конспекты лекций : 16–19.
41. Родригес, Г. (2007). Конспект лекций по обобщенным линейным моделям. стр. Глава 3, стр. 45.
42. Гарет Джеймс; Даниэла Виттен; Тревор Хэсти; Роберт Тибширани (2013). Введение в статистическое обучение. Спрингер. п. 6.
43. Похар, Майя; Блас, Матея; Терк, Сандра (2004). «Сравнение логистической регрессии и линейного дискриминантного анализа: моделирование». Методолошки Звездки . 1 (1).
44. Крамер 2002, стр. 3–5.
45. Ферхюльст, Пьер-Франсуа (1838). «Обратите внимание на то, что население стремится к росту сына» (PDF) . Переписка по математике и физике . 10 : 113–121 . Проверено 3 декабря 2014 г.
46. Крамер 2002, с. 4: «Он не сказал, как он подогнал кривые».
47. Ферхюльст, Пьер-Франсуа (1845). «Математические исследования закона роста населения». Новые мемуары Королевской академии наук и изящной словесности Брюсселя . 18 . Проверено 18 февраля 2013 г.
48. Крамер 2002, с. 4.
49. Крамер 2002, с. 7.
50. Крамер 2002, с. 6.
51. Крамер 2002, с. 6–7.
52. Крамер 2002, с. 5.
53. Крамер 2002, с. 7–9.
54. Крамер 2002, с. 9.
55. Крамер 2002, с. 8: «Насколько я понимаю, внедрение логистики в качестве альтернативы обычной функции вероятности — это работа одного человека, Джозефа Берксона (1899–1982)…»
56. Крамер 2002, с. 11.
57. Крамер 2002, с. 13.
58. Макфадден, Дэниел (1973). «Условный логит-анализ поведения качественного выбора» (PDF) . В П. Зарембке (ред.). Границы в эконометрике . Нью-Йорк: Академическая пресса. стр. 105–142. Архивировано из оригинала (PDF) 27 ноября 2018 г. Проверено 20 апреля 2019 г.

Источники

• Берксон, Джозеф (1944). «Применение логистической функции к биоанализу». Журнал Американской статистической ассоциации . 39 (227): 357–365. дои : 10.1080/01621459.1944.10500699. JSTOR  2280041.
• Берксон, Джозеф (1951). «Почему я предпочитаю логиты пробитам». Биометрия . 7 (4): 327–339. дои : 10.2307/3001655. ISSN  0006-341X. JSTOR  3001655.
• Блисс, CI (1934). «Метод пробитов». Наука . 79 (2037): 38–39. Бибкод : 1934Sci....79...38B. дои : 10.1126/science.79.2037.38. PMID  17813446. Эти произвольные единицы вероятности получили название «пробиты».
• Кокс, Дэвид Р. (1958). «Регрессионный анализ бинарных последовательностей (с обсуждением)». JR Stat Soc B. 20 (2): 215–242. JSTOR  2983890.
• Кокс, Дэвид Р. (1966). «Некоторые процедуры, связанные с кривой качественного логистического ответа». В Ф. Н. Дэвиде (ред.). Исследовательские статьи по теории вероятности и статистике (Festschrift for J. Neyman) . Лондон: Уайли. стр. 55–71.
• Крамер, Дж. С. (2002). Истоки логистической регрессии (PDF) (Технический отчет). Том. 119. Институт Тинбергена. стр. 167–178. дои : 10.2139/ssrn.360300.
  • Опубликовано: Крамер, Дж.С. (2004). «Ранние истоки логит-модели». Исследования по истории и философии науки. Часть C: Исследования по истории и философии биологических и биомедицинских наук . 35 (4): 613–626. дои :10.1016/j.shpsc.2004.09.003.
• Фишер, Р.А. (1935). «Случай нулевых выживших в анализах пробита». Анналы прикладной биологии . 22 : 164–165. doi :10.1111/j.1744-7348.1935.tb07713.x. Архивировано из оригинала 30 апреля 2014 г.
• Гаддум, Джон Х. (1933). Отчеты о биологических стандартах: методы биологического анализа в зависимости от квантового ответа. III . Канцелярский офис HM. ОСЛК  808240121.
• Тейл, Анри (1969). «Мультиномиальное расширение линейной логит-модели». Международное экономическое обозрение . 10 (3): 251–59. дои : 10.2307/2525642. JSTOR  2525642.
• Перл, Раймонд; Рид, Лоуэлл Дж. (июнь 1920 г.). «О темпах роста населения Соединенных Штатов с 1790 года и его математическом представлении». Труды Национальной академии наук . 6 (6): 275–288. Бибкод : 1920PNAS....6..275P. дои : 10.1073/pnas.6.6.275 . ПМЦ  1084522 . ПМИД  16576496.
• Уилсон, Э.Б .; Вустер, Дж. (1943). «Определение LD50 и его ошибка отбора проб в биоанализе». Труды Национальной академии наук Соединенных Штатов Америки . 29 (2): 79–85. Бибкод : 1943PNAS...29...79W. дои : 10.1073/pnas.29.2.79 . ПМЦ  1078563 . ПМИД  16588606.

• Агрести, Алан. (2002). Категориальный анализ данных . Нью-Йорк: Wiley-Interscience. ISBN 978-0-471-36093-3.
• Амемия, Такеши (1985). «Модели качественного ответа». Продвинутая эконометрика . Оксфорд: Бэзил Блэквелл. стр. 267–359. ISBN 978-0-631-13345-2.
• Балакришнан, Н. (1991). Справочник по логистическому распределению . Марсель Деккер, Inc. ISBN 978-0-8247-8587-1.
• Гурьеру, Кристиан (2000). «Простая дихотомия». Эконометрика качественных зависимых переменных . Нью-Йорк: Издательство Кембриджского университета. стр. 6–37. ISBN 978-0-521-58985-7.
• Грин, Уильям Х. (2003). Эконометрический анализ, пятое издание . Прентис Холл. ISBN 978-0-13-066189-0.
• Хильбе, Джозеф М. (2009). Модели логистической регрессии . Чепмен и Холл/CRC Press. ISBN 978-1-4200-7575-5.
• Хосмер, Дэвид (2013). Прикладная логистическая регрессия . Хобокен, Нью-Джерси: Уайли. ISBN 978-0-470-58247-3.
• Хауэлл, Дэвид С. (2010). Статистические методы в психологии, 7-е изд . Бельмонт, Калифорния; Томсон Уодсворт. ISBN 978-0-495-59786-5.
• Педуцци, П.; Дж. Конкато; Э. Кемпер; Т. Р. Холфорд; А. Р. Файнштейн (1996). «Моделирующее исследование количества событий на переменную в логистическом регрессионном анализе». Журнал клинической эпидемиологии . 49 (12): 1373–1379. дои : 10.1016/s0895-4356(96)00236-3 . ПМИД  8970487.
• Берри, Майкл Дж.А.; Линофф, Гордон (1997). Методы интеллектуального анализа данных для маркетинга, продаж и поддержки клиентов . Уайли.

Внешние ссылки

• СМИ, связанные с логистической регрессией, на Викискладе?
• Лекция по эконометрике (тема: Логит-модель) на YouTube , автор Марк Тома
• Учебник по логистической регрессии
• mlelr: программное обеспечение на C для учебных целей.