Коэффициент детерминации

Индикатор того, насколько хорошо точки данных соответствуют линии или кривой.

Обычная регрессия закона Оукена по методу наименьших квадратов . Поскольку линия регрессии не сильно пропускает ни одну из точек, R ² регрессии относительно высока.

Сравнение оценки Тейла – Сена (черный) и простой линейной регрессии (синий) для набора точек с выбросами . Из-за большого количества выбросов ни одна из линий регрессии не соответствует данным хорошо, о чем свидетельствует тот факт, что ни одна из них не дает очень высокого R ² .

В статистике коэффициент детерминации , обозначаемый R ² или r ² и произносимый как «R в квадрате», представляет собой долю изменения зависимой переменной, которую можно предсказать на основе независимой переменной (переменных).

Это статистика, используемая в контексте статистических моделей , основной целью которых является либо прогнозирование будущих результатов, либо проверка гипотез на основе другой соответствующей информации. Он обеспечивает оценку того, насколько хорошо наблюдаемые результаты воспроизводятся моделью, на основе доли общей вариации результатов, объясненной моделью. ^{[1] [2] [3]}

Существует несколько определений R2 ^, которые лишь иногда эквивалентны. Один класс таких случаев включает в себя простую линейную регрессию , где вместо R ² используется r ² . Когда включен только перехват , тогда r ² представляет собой просто квадрат выборочного коэффициента корреляции (т. е. r ) между наблюдаемыми результатами и наблюдаемыми значениями предикторов. ^[4] Если включены дополнительные регрессоры , R ² представляет собой квадрат коэффициента множественной корреляции . В обоих случаях коэффициент детерминации обычно находится в диапазоне от 0 до 1.

Есть случаи, когда R ² может давать отрицательные значения. Это может возникнуть, когда прогнозы, которые сравниваются с соответствующими результатами, не были получены в результате процедуры подбора модели с использованием этих данных. Даже если использовалась процедура подбора модели, R ² все равно может быть отрицательным, например, когда линейная регрессия проводится без включения точки пересечения ^[5] или когда для подбора данных используется нелинейная функция. ^[6] В случаях, когда возникают отрицательные значения, среднее значение данных обеспечивает лучшее соответствие результатам, чем значения подобранной функции, согласно этому конкретному критерию.

Коэффициент детерминации может быть более (интуитивно) информативным, чем MAE , MAPE , MSE и RMSE при оценке регрессионного анализа , поскольку первый может быть выражен в процентах, тогда как вторые меры имеют произвольные диапазоны. Он также оказался более устойчивым к плохим соответствиям по сравнению с SMAPE на тестовых наборах данных в статье. ^[7]

При оценке согласия смоделированных ( Y _pred ) и измеренных ( Y _obs ) значений нецелесообразно основывать это на R ² линейной регрессии (т. е. Y _obs = m · Y _pred + b ). ^{[ нужна ссылка ]} R ² количественно определяет степень любой линейной корреляции между Y _obs и Y _pred , в то время как для оценки согласия следует принимать во внимание только одну конкретную линейную корреляцию: Y obs ₌ 1 · Y _pred + 0 (т.е. линия 1:1). ^{[8] [9]}

Определения

${\displaystyle R^{2}=1-{\frac {\color {blue}{SS_{\text{res}}}}{\color {red}{SS_{\text{tot}}}}}}$
Чем лучше линейная регрессия (справа) соответствует данным по сравнению с простым средним значением (на левом графике), тем ближе значение к 1. Области синих квадратов представляют собой квадраты остатков по отношению к линейному регресс. Площади красных квадратов представляют собой квадраты остатков относительно среднего значения. ${\displaystyle R^{2}}$

Набор данных имеет n значений, отмеченных y ₁ ,..., y _n (вместе известных как y _i или вектор y = [ y ₁ ,..., y _n ] ^T ), каждое из которых связано с подобранным (или смоделированным) , или предсказанное) значение f ₁ ,..., f _n (известное как fi _, или иногда ŷ _i , как вектор f ).

Определите остатки как e _i = y _i - f _i (образуя вектор e ).

Если – среднее значение наблюдаемых данных: ${\displaystyle {\bar {y}}}$

$${\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$$

суммы квадратов

• Сумма квадратов остатков, называемая также остаточной суммой квадратов :
  $${\displaystyle SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^{2}\,}$$
• Общая сумма квадратов (пропорциональная дисперсии данных ):
  $${\displaystyle SS_{\text{tot}}=\sum _{i}(y_{i}-{\bar {y}})^{2}}$$

Наиболее общее определение коэффициента детерминации:

$${\displaystyle R^{2}=1-{SS_{\rm {res}} \over SS_{\rm {tot}}}}$$

В лучшем случае смоделированные значения точно соответствуют наблюдаемым значениям, что приводит к и . Базовая модель, которая всегда предсказывает , будет иметь . Модели, прогнозы которых хуже этого базового уровня, будут иметь отрицательный результат . ${\displaystyle SS_{\text{res}}=0}$ ${\displaystyle R^{2}=1}$ ${\displaystyle {\bar {y}}}$ ${\displaystyle R^{2}=0}$ ${\displaystyle R^{2}}$

Связь с необъяснимой дисперсией

В общей форме можно увидеть, что R ² связан с долей необъяснимой дисперсии (FVU), поскольку второй член сравнивает необъяснимую дисперсию (дисперсию ошибок модели) с общей дисперсией (данных):

$${\displaystyle R^{2}=1-{\text{FVU}}}$$

Как объяснили дисперсию

Большее значение R ² подразумевает более успешную регрессионную модель. ^{[4] : 463} Предположим, R ² = 0,49. Это означает, что 49% изменчивости зависимой переменной в наборе данных учтено, а оставшийся 51% изменчивости все еще не учтен. Для регрессионных моделей сумма квадратов регрессии, также называемая объясненной суммой квадратов , определяется как

${\displaystyle SS_{\text{reg}}=\sum _{i}(f_{i}-{\bar {y}})^{2}}$

В некоторых случаях, как в простой линейной регрессии , общая сумма квадратов равна сумме двух других сумм квадратов, определенных выше:

${\displaystyle SS_{\text{res}}+SS_{\text{reg}}=SS_{\text{tot}}}$

См. Разделение в общей модели МНК для получения этого результата для одного случая, когда это соотношение выполняется. Когда это соотношение действительно выполняется, приведенное выше определение R ² эквивалентно

${\displaystyle R^{2}={\frac {SS_{\text{reg}}}{SS_{\text{tot}}}}={\frac {SS_{\text{reg}}/n}{SS_{\text{tot}}/n}}}$

где n — количество наблюдений (случаев) над переменными.

В этой форме R ² выражается как отношение объясненной дисперсии (дисперсии предсказаний модели, которая равна SS _reg / n ) к общей дисперсии (выборочной дисперсии зависимой переменной, которая равна SS _tot / n ).

Это разделение суммы квадратов справедливо, например, когда значения модели ƒ _i были получены с помощью линейной регрессии . Более мягкое достаточное условие имеет вид: Модель имеет вид

${\displaystyle f_{i}={\widehat {\alpha }}+{\widehat {\beta }}q_{i}\,}$

где q _i - произвольные значения, которые могут зависеть или не зависеть от i или других свободных параметров (обычный выбор q _i  =  x _i - это всего лишь один частный случай), а оценки коэффициентов и получаются путем минимизации остаточной суммы квадратов . ${\displaystyle {\widehat {\alpha }}}$ ${\displaystyle {\widehat {\beta }}}$

Этот набор условий является важным и имеет ряд последствий для свойств подобранных остатков и смоделированных значений. В частности, в этих условиях:

${\displaystyle {\bar {f}}={\bar {y}}.\,}$

Как квадрат коэффициента корреляции

В линейной множественной регрессии по методу наименьших квадратов с оценкой члена пересечения R ² равен квадрату коэффициента корреляции Пирсона между наблюдаемыми и смоделированными (прогнозируемыми) значениями данных зависимой переменной. ${\displaystyle y}$ ${\displaystyle f}$

В линейной регрессии наименьших квадратов с одним объяснителем, но без члена-члена , это также равно квадрату коэффициента корреляции Пирсона зависимой переменной и объясняющей переменной. ${\displaystyle y}$ ${\displaystyle x.}$

Его не следует путать с коэффициентом корреляции между двумя объясняющими переменными , определяемым как

${\displaystyle \rho _{{\widehat {\alpha }},{\widehat {\beta }}}={\operatorname {cov} \left({\widehat {\alpha }},{\widehat {\beta }}\right) \over \sigma _{\widehat {\alpha }}\sigma _{\widehat {\beta }}},}$

где ковариация между двумя оценками коэффициентов, а также их стандартные отклонения получаются из ковариационной матрицы оценок коэффициентов . ${\displaystyle (X^{T}X)^{-1}}$

В более общих условиях моделирования, когда прогнозируемые значения могут быть сгенерированы на основе модели, отличной от линейной регрессии наименьших квадратов, значение R ² может быть рассчитано как квадрат коэффициента корреляции между исходными и смоделированными значениями данных. В этом случае значение не является прямой мерой того, насколько хороши смоделированные значения, а скорее мерой того, насколько хорош предиктор может быть построен на основе смоделированных значений (путем создания пересмотренного предиктора формы α  +  βƒ _i ). ^{[ нужна цитата ]} Согласно Эверитту, ^[10] это использование представляет собой определение термина «коэффициент детерминации»: квадрат корреляции между двумя (общими) переменными. ${\displaystyle y}$ ${\displaystyle f}$

Интерпретация

R ² является мерой соответствия модели. ^[11] В регрессии коэффициент детерминации R ² является статистической мерой того, насколько хорошо прогнозы регрессии приближаются к реальным точкам данных. R ² из 1 указывает на то, что прогнозы регрессии идеально соответствуют данным.

Значения R ² вне диапазона от 0 до 1 возникают, когда модель соответствует данным хуже, чем худший возможный предиктор наименьших квадратов (эквивалент горизонтальной гиперплоскости на высоте, равной среднему значению наблюдаемых данных). Это происходит, когда была выбрана неверная модель или по ошибке были применены бессмысленные ограничения. Если используется уравнение 1 Кволсета ^[12] (это уравнение используется чаще всего), R ² может быть меньше нуля. Если используется уравнение 2 Кволсета, R ² может быть больше единицы.

Во всех случаях, когда используется R ² , предикторы рассчитываются с помощью обычной регрессии наименьших квадратов, то есть путем минимизации SS _res . В этом случае R ² увеличивается с увеличением количества переменных в модели ( R ² монотонно увеличивается с увеличением количества включенных переменных — он никогда не уменьшится). Это иллюстрирует недостаток одного из возможных вариантов использования R ² , когда можно продолжать добавлять переменные ( регрессия кухонной мойки ) для увеличения значения R ² . Например, если кто-то пытается спрогнозировать продажи модели автомобиля, исходя из расхода бензина, цены и мощности двигателя, можно включить такие несущественные факторы, как первая буква названия модели или рост ведущего инженера, проектирующего модель. автомобиль, потому что R ² никогда не уменьшится при добавлении переменных и, скорее всего, увеличится только по случайности.

Это приводит к альтернативному подходу рассмотрения скорректированного R2. Объяснение этой статистики почти такое же, как и R ² , но оно ухудшает статистику, поскольку в модель включены дополнительные переменные. Для случаев, отличных от аппроксимации обычным методом наименьших квадратов, статистика R ² может быть рассчитана, как указано выше, и все равно может быть полезной мерой. Если аппроксимация осуществляется методом взвешенных наименьших квадратов или обобщенным методом наименьших квадратов , альтернативные версии R ² могут быть рассчитаны в соответствии с этими статистическими основами, в то время как «необработанный» R ² все еще может быть полезен, если его легче интерпретировать. Значения R ² можно рассчитать для любого типа прогнозной модели, которая не обязательно должна иметь статистическую основу.

В множественной линейной модели

Рассмотрим линейную модель с более чем одной объясняющей переменной вида

${\displaystyle Y_{i}=\beta _{0}+\sum _{j=1}^{p}\beta _{j}X_{i,j}+\varepsilon _{i},}$

где для i- го случая – переменная ответа, – p- регрессоры, и – средний член с нулевой ошибкой . Величины представляют собой неизвестные коэффициенты, значения которых оцениваются методом наименьших квадратов . Коэффициент детерминации R ² является мерой глобального соответствия модели. В частности, R ² является элементом [0, 1] и представляет собой долю изменчивости в Y _i , которую можно отнести к некоторой линейной комбинации регрессоров ( объяснительных переменных ) в X. ^[13] ${\displaystyle {Y_{i}}}$ ${\displaystyle X_{i,1},\dots ,X_{i,p}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle \beta _{0},\dots ,\beta _{p}}$

R ² часто интерпретируется как доля вариации ответа, «объясняемая» регрессорами в модели. Таким образом, R ²  = 1 указывает на то, что подобранная модель объясняет всю изменчивость в , тогда как R ²  = 0 указывает на отсутствие «линейной» зависимости (для регрессии по прямой это означает, что модель прямой линии представляет собой постоянную линию (наклон = 0, пересечение =  ) между переменной ответа и регрессорами). Внутреннее значение, такое как R ²  = 0,7, можно интерпретировать следующим образом: «Семьдесят процентов дисперсии переменной отклика можно объяснить объясняющими переменными. Остальные тридцать процентов можно отнести к неизвестным, скрытым переменным или внутренней изменчивости». ${\displaystyle y}$ ${\displaystyle {\bar {y}}}$

Предостережение, которое применимо к R ² , как и к другим статистическим описаниям корреляции и ассоциации, заключается в том, что « корреляция не подразумевает причинно-следственную связь ». Другими словами, хотя корреляции иногда могут дать ценные подсказки для выявления причинно-следственных связей между переменными, ненулевая предполагаемая корреляция между двумя переменными сама по себе не является свидетельством того, что изменение значения одной переменной приведет к изменениям значений других переменных. другие переменные. Например, практика ношения спичек (или зажигалки) коррелирует с заболеваемостью раком легких, но ношение спичек не вызывает рак (в стандартном смысле «причины»).

В случае одного регрессора, аппроксимируемого методом наименьших квадратов, R ² представляет собой квадрат коэффициента корреляции момента произведения Пирсона, связывающего регрессор и переменную отклика. В более общем смысле, R ² представляет собой квадрат корреляции между построенным предиктором и переменной ответа. При наличии более чем одного регрессора R ² можно назвать коэффициентом множественной детерминации .

Инфляция в рублях 2

В регрессии наименьших квадратов с использованием типичных данных R ² как минимум слабо возрастает с увеличением числа регрессоров в модели. Поскольку увеличение количества регрессоров увеличивает значение R ² , сам по себе R ² не может использоваться для значимого сравнения моделей с очень разным количеством независимых переменных. Для значимого сравнения двух моделей можно провести F-тест по остаточной сумме квадратов ^{[ нужна ссылка ]} , аналогичный F-тестам в причинности Грейнджера , хотя это не всегда уместно ^{[ нужны дальнейшие объяснения ]} . Напоминая об этом, некоторые авторы обозначают R ² через R _q ² , где q — количество столбцов в X (количество объяснителей, включая константу).

Чтобы продемонстрировать это свойство, сначала вспомните, что целью линейной регрессии по методу наименьших квадратов является

${\displaystyle \min _{b}SS_{\text{res}}(b)\Rightarrow \min _{b}\sum _{i}(y_{i}-X_{i}b)^{2}\,}$

где X _i - вектор-строка значений объясняющих переменных для случая i, а b - вектор-столбец коэффициентов соответствующих элементов X _i .

Оптимальное значение цели немного меньше по мере того, как добавляется больше объясняющих переменных и, следовательно, добавляются дополнительные столбцы (матрицы объяснительных данных, i -я строка которой равна X _i ), поскольку менее ограниченная минимизация приводит к оптимальной стоимости, которая равна немного меньше, чем более ограниченная минимизация. Учитывая предыдущий вывод и учитывая, что оно зависит только от y , свойство неубывания R ² следует непосредственно из определения, приведенного выше. ${\displaystyle X}$ ${\displaystyle SS_{tot}}$

Интуитивная причина того, что использование дополнительной объясняющей переменной не может снизить ^R2 , ^{заключается} в следующем: минимизация эквивалентна максимизации R2 . Когда включена дополнительная переменная, данные всегда имеют возможность присвоить ей расчетный коэффициент, равный нулю, оставив прогнозируемые значения и R ² неизменными. Единственный способ, при котором задача оптимизации даст ненулевой коэффициент, — это улучшить R ² . ${\displaystyle SS_{\text{res}}}$

Вышеизложенное дает аналитическое объяснение инфляции R ² . Далее ниже показан пример, основанный на обычном методе наименьших квадратов с геометрической точки зрения. ^[14]

Это пример остатков регрессионных моделей в меньших и больших пространствах, основанных на обычной регрессии наименьших квадратов.

Простой случай, который следует рассмотреть в первую очередь:

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\epsilon \,}$

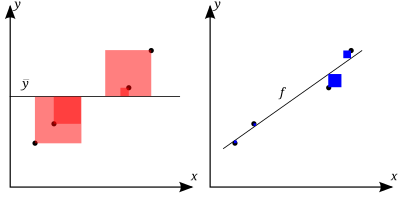
Это уравнение описывает обычную модель регрессии наименьших квадратов с одним регрессором. Прогноз показан красным вектором на рисунке справа. Геометрически это проекция истинного значения на пространство модели (без пересечения). Остаток показан красной линией. ${\displaystyle \mathbb {R} }$

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\beta _{2}\cdot X_{2}+\epsilon \,}$

Это уравнение соответствует обычной модели регрессии наименьших квадратов с двумя регрессорами. Прогноз показан синим вектором на рисунке справа. Геометрически это проекция истинного значения на большее пространство модели (без пересечения). Примечательно, что значения и не такие, как в уравнении для меньшего модельного пространства, если и не являются нулевыми векторами. Следовательно, ожидается, что уравнения будут давать разные предсказания (т. е. ожидается, что синий вектор будет отличаться от красного вектора). Критерий регрессии наименьших квадратов гарантирует минимизацию остатка. На рисунке синяя линия, представляющая остаток, ортогональна пространству модели в , что указывает на минимальное расстояние от пространства. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$ ${\displaystyle \mathbb {R} ^{2}}$

Меньшее модельное пространство является подпространством большего, поэтому остаток меньшей модели гарантированно будет больше. Если сравнить красную и синюю линии на рисунке, то можно увидеть, что синяя линия ортогональна пространству, а любая другая линия будет больше синей. Учитывая расчет для R ² , меньшее значение приведет к большему значению R ² , а это означает, что добавление регрессоров приведет к инфляции R ² . ${\displaystyle SS_{tot}}$

Предостережения

R ² не указывает,:

• независимые переменные являются причиной изменения зависимой переменной ;
• существует смещение по пропущенной переменной ;
• использовалась правильная регрессия ;
• выбран наиболее подходящий набор независимых переменных;
• в данных по объясняющим переменным присутствует коллинеарность ;
• модель можно улучшить, используя преобразованные версии существующего набора независимых переменных;
• данных достаточно, чтобы сделать однозначный вывод.

Расширения

Скорректированный Р 2

Использование скорректированного R ² (одно распространенное обозначение произносится как «R bar в квадрате»; другое — или ) является попыткой объяснить явление автоматического увеличения R ² при добавлении в модель дополнительных объясняющих переменных. Есть много разных способов регулировки. ^[15] Безусловно, наиболее часто используемым, вплоть до того, что его обычно называют просто скорректированным R , является исправление, предложенное Мордехаем Иезекиилем . ^{[15] [16] [17]} Скорректированный R ² определяется как ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle R_{\text{a}}^{2}}$ ${\displaystyle R_{\text{adj}}^{2}}$

${\displaystyle {\bar {R}}^{2}={1-{SS_{\text{res}}/{\text{df}}_{\text{res}} \over SS_{\text{tot}}/{\text{df}}_{\text{tot}}}}}$

где df _res — это степени свободы оценки дисперсии совокупности вокруг модели, а df _tot — это степени свободы оценки дисперсии совокупности вокруг среднего значения. df _res определяется размером выборки n и количеством переменных p в модели: df _res = n  −  p . df _tot задается таким же образом, но при этом p равно единице для среднего значения, т.е. df _tot = n  - 1.

Подставляя степени свободы и используя определение R ² , его можно переписать как:

${\displaystyle {\bar {R}}^{2}=1-(1-R^{2}){n-1 \over n-p-1}}$

где p — общее количество объясняющих переменных в модели, ^[18] и n — размер выборки.

Скорректированный R ² может быть отрицательным, и его значение всегда будет меньше или равно значению R ² . В отличие от R ² , скорректированный R ² увеличивается только тогда, когда увеличение R ² (из-за включения новой объясняющей переменной) больше, чем можно было бы ожидать случайно. Если набор объясняющих переменных с заранее определенной иерархией важности вводится в регрессию по одной, при этом скорректированный R ² вычисляется каждый раз, то уровень, на котором скорректированный R ² достигает максимума, а затем снижается, будет регрессией. с идеальным сочетанием наилучшего соответствия без лишних/ненужных условий.

Схема вклада систематической ошибки и дисперсии в общую ошибку

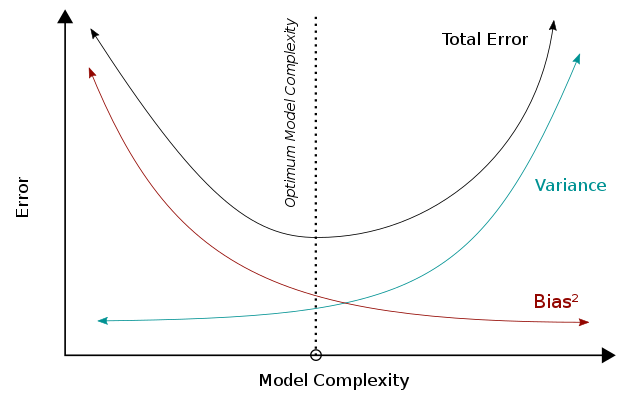
Скорректированный R ² можно интерпретировать как пример компромисса между смещением и дисперсией . Когда мы рассматриваем производительность модели, меньшая ошибка означает лучшую производительность. Когда модель становится более сложной, дисперсия будет увеличиваться, тогда как квадрат смещения будет уменьшаться, и эти две метрики в сумме образуют общую ошибку. Сочетая эти две тенденции, компромисс между смещением и дисперсией описывает взаимосвязь между производительностью модели и ее сложностью, которая показана в виде U-образной кривой справа. В частности, для скорректированного R ² сложность модели (т.е. количество параметров) влияет на R ² и термин/разрыв и тем самым отражает их атрибуты в общей производительности модели.

R ² можно интерпретировать как дисперсию модели, на которую влияет сложность модели. Высокий R ² указывает на меньшую ошибку смещения, поскольку модель может лучше объяснить изменение Y с помощью предикторов. По этой причине мы делаем меньше (ошибочных) предположений, и это приводит к меньшей ошибке смещения. Между тем, чтобы учесть меньше предположений, модель имеет тенденцию быть более сложной. Исходя из компромисса смещения и дисперсии, более высокая сложность приведет к уменьшению смещения и лучшей производительности (ниже оптимальной линии). В , член (1- R ² ) будет ниже с высокой сложностью и приведет к более высокому значению , что постоянно указывает на лучшую производительность. ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$

С другой стороны, на термин/член гидроразрыва обратное влияние оказывает сложность модели. Срок/разрыв увеличится при добавлении регрессоров (т. е. увеличится сложность модели) и приведет к ухудшению производительности. На основании компромисса между смещением и дисперсией более высокая сложность модели (за пределами оптимальной линии) приводит к увеличению ошибок и снижению производительности.

Учитывая расчет , большее количество параметров приведет к увеличению R ² и приведет к увеличению . Тем не менее, добавление большего количества параметров приведет к увеличению срока/разрыва и, следовательно, уменьшению . Эти две тенденции создают обратную U-образную зависимость между сложностью модели и , которая согласуется с U-образной тенденцией зависимости сложности модели от общей производительности. В отличие от R ² , который всегда будет увеличиваться при увеличении сложности модели, он будет увеличиваться только тогда, когда смещение, устраняемое добавленным регрессором, превышает дисперсию, вносимую одновременно. Таким образом , использование вместо R ² может предотвратить переобучение. ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$ ${\displaystyle {\bar {R}}^{2}}$

Следуя той же логике, скорректированный R ² можно интерпретировать как менее смещенную оценку генеральной совокупности R ² , тогда как наблюдаемая выборка R ² представляет собой положительно смещенную оценку стоимости генеральной совокупности. ^[19] Скорректированный R ² более подходит при оценке соответствия модели (дисперсия зависимой переменной, учитываемая независимыми переменными) и при сравнении альтернативных моделей на этапе выбора признаков при построении модели. ^[19]

Принцип скорректированной статистики R ² можно увидеть, переписав обычный R ² как

${\displaystyle R^{2}={1-{{\textit {VAR}}_{\text{res}} \over {\textit {VAR}}_{\text{tot}}}}}$

где и представляют собой выборочные дисперсии оцененных остатков и зависимой переменной соответственно, которые можно рассматривать как смещенные оценки генеральных дисперсий ошибок и зависимой переменной. Эти оценки заменяются статистически несмещенными версиями: и . ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/n}$ ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/n}$ ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/(n-p)}$ ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/(n-1)}$

Несмотря на использование несмещенных оценок генеральной дисперсии ошибки и зависимой переменной, скорректированный R ² не является несмещенной оценкой генеральной совокупности R ² , ^[19] что является результатом использования генеральной дисперсии ошибок и зависимой переменной вместо оценки их. Ингрэм Олкин и Джон В. Пратт получили несмещенную оценку минимальной дисперсии для совокупности R ² , ^[20] которая известна как оценка Олкина-Пратта. Сравнение различных подходов к корректировке R ² пришло к выводу, что в большинстве ситуаций либо приблизительная версия оценки Олкина-Пратта ^[19] , либо точная версия оценки Олкина-Пратта ^[21] должна быть предпочтительнее скорректированного (Иезекииля) R ² .

Коэффициент частичной детерминации

Коэффициент частичной детерминации можно определить как долю вариации, которую невозможно объяснить в сокращенной модели, но можно объяснить с помощью предикторов, указанных в полной (полной) модели. ^{[22] [23] [24]} Этот коэффициент используется для определения того, могут ли один или несколько дополнительных предикторов быть полезны в более подробной регрессионной модели.

Расчет частичного R ² относительно прост после оценки двух моделей и создания для них таблиц ANOVA . Расчет для частичного R ² следующий:

${\displaystyle {\frac {SS_{\text{ res, reduced}}-SS_{\text{ res, full}}}{SS_{\text{ res, reduced}}}},}$

что аналогично обычному коэффициенту детерминации:

${\displaystyle {\frac {SS_{\text{tot}}-SS_{\text{res}}}{SS_{\text{tot}}}}.}$

Обобщение и декомпозиция R 2

Как объяснялось выше, эвристики выбора модели, такие как скорректированный критерий и F-тест, проверяют, достаточно ли увеличивается общая сумма , чтобы определить, следует ли добавить в модель новый регрессор. Если к модели добавляется регрессор, который сильно коррелирует с другими уже включенными регрессорами, то общая сумма вряд ли увеличится, даже если новый регрессор имеет значение. В результате вышеупомянутые эвристики будут игнорировать соответствующие регрессоры, когда взаимная корреляция высока. ^[25] ${\displaystyle R^{2}}$ ${\displaystyle R^{2}}$ ${\displaystyle R^{2}}$

Геометрическое представление . ${\displaystyle r^{2}}$

В качестве альтернативы можно разложить обобщенную версию, чтобы количественно оценить релевантность отклонения от гипотезы. ^[25] Как показывает Хорнвег (2018), некоторые средства оценки усадки , такие как байесовская линейная регрессия , гребневая регрессия и (адаптивное) лассо , используют это разложение, когда они постепенно сокращают параметры от неограниченных решений OLS до гипотетических значений. . Давайте сначала определим модель линейной регрессии как ${\displaystyle R^{2}}$ ${\displaystyle R^{2}}$

${\displaystyle y=X\beta +\varepsilon .}$

Предполагается, что матрица стандартизирована с помощью Z-показателей и что вектор-столбец центрирован так, чтобы иметь нулевое среднее значение. Пусть вектор-столбец относится к предполагаемым параметрам регрессии, а вектор-столбец обозначает оцененные параметры. Затем мы можем определить ${\displaystyle X}$ ${\displaystyle y}$ ${\displaystyle \beta _{0}}$ ${\displaystyle b}$

${\displaystyle R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(y-X\beta _{0})'(y-X\beta _{0})}}.}$

Значение 75 % означает, что точность в выборке повышается на 75 %, если вместо гипотетических значений используются решения, оптимизированные для данных . В частном случае, когда вектор нулей, мы снова получаем традиционное решение. ${\displaystyle R^{2}}$ ${\displaystyle b}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle R^{2}}$

Индивидуальный эффект отклонения от гипотезы можно вычислить с помощью («R-outer»). Эта матрица времен определяется выражением ${\displaystyle R^{2}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle R^{\otimes }=(X'{\tilde {y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},}$

где . Диагональные элементы точно в сумме составляют . Если регрессоры некоррелированы и представляют собой вектор нулей, то диагональный элемент просто соответствует значению между и . Когда регрессоры и коррелируют, может увеличиться за счет уменьшения . В результате диагональные элементы могут быть меньше 0 и, в более исключительных случаях, больше 1. Чтобы справиться с такими неопределенностями, некоторые средства оценки усадки неявно берут средневзвешенное значение диагональных элементов для количественной оценки релевантности отклонения от предполагаемое значение. ^[25] Нажмите на лассо , чтобы увидеть пример. ${\displaystyle {\tilde {y}}_{0}=y-X\beta _{0}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle R^{2}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle j^{\text{th}}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle r^{2}}$ ${\displaystyle x_{j}}$ ${\displaystyle y}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{j}}$ ${\displaystyle R_{ii}^{\otimes }}$ ${\displaystyle R_{jj}^{\otimes }}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle R^{\otimes }}$

R 2 в логистической регрессии

В случае логистической регрессии , обычно подходящей по максимальному правдоподобию , существует несколько вариантов псевдо-R ² .

Одним из них является обобщенный R2 ^, первоначально предложенный Коксом и Снеллом ^[26] и независимо Маги: ^[27]

${\displaystyle R^{2}=1-\left({{\mathcal {L}}(0) \over {\mathcal {L}}({\widehat {\theta }})}\right)^{2/n}}$

где — правдоподобие модели только с отрезком, — правдоподобие оцененной модели (т. е. модели с заданным набором оценок параметров), а n — размер выборки. Его легко переписать так: ${\displaystyle {\mathcal {L}}(0)}$ ${\displaystyle {{\mathcal {L}}({\widehat {\theta }})}}$

${\displaystyle R^{2}=1-e^{{\frac {2}{n}}(\ln({\mathcal {L}}(0))-\ln({\mathcal {L}}({\widehat {\theta }}))}=1-e^{-D/n}}$

где D — тестовая статистика теста отношения правдоподобия .

Нико Нагелькерке отметил, что он обладает следующими свойствами: ^{[28] [23]}

1. Это соответствует классическому коэффициенту детерминации, когда оба могут быть вычислены;
2. Его значение максимизируется за счет оценки максимального правдоподобия модели;
3. Он асимптотически не зависит от размера выборки;
4. Интерпретация – это доля вариаций, объясняемая моделью;
5. Значения находятся в диапазоне от 0 до 1, где 0 означает, что модель не объясняет никаких изменений, а 1 означает, что она полностью объясняет наблюдаемые изменения;
6. У него нет никакой единицы.

Однако в случае логистической модели, где значение R 2 не может быть больше 1, R ² находится в диапазоне от 0 до : таким образом, Нагелькерке предложил возможность определить масштабированный R ² как R ² / R ² _max . ^[23] ${\displaystyle {\mathcal {L}}({\widehat {\theta }})}$ ${\displaystyle R_{\max }^{2}=1-({\mathcal {L}}(0))^{2/n}}$

Сравнение с нормой остатков

Иногда для определения степени соответствия используется норма остатков. Этот член рассчитывается как квадратный корень из суммы квадратов остатков :

${\displaystyle {\text{norm of residuals}}={\sqrt {SS_{\text{res}}}}=\|e\|.}$

И R ² , и норма остатков имеют свои относительные преимущества. Для анализа методом наименьших квадратов R ² варьируется от 0 до 1, причем большие числа указывают на лучшее соответствие, а 1 — на идеальное соответствие. Норма остатков варьируется от 0 до бесконечности, при этом меньшие числа указывают на лучшее соответствие, а ноль — на идеальное соответствие. Одним из преимуществ и недостатков R ² является то, что термин действует для нормализации значения. Если все значения y _i умножить на константу, норма остатков также изменится на эту константу, но R ² останется прежним. В качестве базового примера для линейного метода наименьших квадратов, подходящего к набору данных: ${\displaystyle SS_{\text{tot}}}$

R ² = 0,998, норма остатков = 0,302.

Если все значения у умножить на 1000 (например, при смене префикса СИ ), то R ² останется прежним, но норма остатков = 302.

Еще одним однопараметрическим индикатором соответствия является среднеквадратическое отклонение остатков или стандартное отклонение остатков. Для приведенного выше примера это значение будет равно 0,135, учитывая, что подгонка была линейной с непринудительным пересечением. ^[29]

История

Создание коэффициента детерминации приписывается генетику Сьюэллу Райту и впервые было опубликовано в 1921 году. ^[30]

Смотрите также

• квартет Анскомба
• Доля дисперсии необъяснима
• Хорошая посадка
• Коэффициент эффективности модели Нэша – Сатклиффа ( гидрологические приложения )
• Коэффициент корреляции момента произведения Пирсона
• Пропорциональное сокращение потерь
• Проверка регрессионной модели
• Среднеквадратичное отклонение
• Пошаговая регрессия

Примечания

1. Сталь, РГД; Торри, Дж. Х. (1960). Принципы и процедуры статистики с особым упором на биологические науки . МакГроу Хилл .
2. Гланц, Стэнтон А.; Слинкер, БК (1990). Основы прикладной регрессии и дисперсионного анализа . МакГроу-Хилл. ISBN 978-0-07-023407-9.
3. Дрейпер, Северная Каролина; Смит, Х. (1998). Прикладной регрессионный анализ . Уайли-Интерсайенс. ISBN 978-0-471-17082-2.
4. Девор, Джей Л. (2011). Вероятность и статистика для техники и наук (8-е изд.). Бостон, Массачусетс: Cengage Learning. стр. 508–510. ISBN 978-0-538-73352-6.
5. Бартен, Антон П. (1987). «Коэффициент детерминации регрессии без постоянного члена». Ин Хейманс, Ристо; Нойдекер, Хайнц (ред.). Практика эконометрики . Дордрехт: Клювер. стр. 181–189. ISBN 90-247-3502-5.
6. Колин Кэмерон, А.; Виндмейер, Франк А.Г. (1997). «R-квадратная мера согласия для некоторых распространенных моделей нелинейной регрессии». Журнал эконометрики . 77 (2): 1790–2. дои : 10.1016/S0304-4076(96)01818-0.
7. Чикко, Давиде; Уорренс, Маттейс Дж.; Юрман, Джузеппе (2021). «Коэффициент детерминации R-квадрат более информативен, чем SMAPE, MAE, MAPE, MSE и RMSE при оценке регрессионного анализа». PeerJ Информатика . 7 (e623): e623. дои : 10.7717/peerj-cs.623 . ПМЦ 8279135 . ПМИД  34307865. 
8. Легаты, ДР; Маккейб, Дж.Дж. (1999). «Оценка использования показателей согласия при проверке гидрологических и гидроклиматических моделей». Водный ресурс. Рез . 35 (1): 233–241. Бибкод : 1999WRR....35..233L. дои : 10.1029/1998WR900018. S2CID  128417849.
9. Риттер, А.; Муньос-Карпена, Р. (2013). «Оценка эффективности гидрологических моделей: статистическая значимость для снижения субъективности в оценках согласия». Журнал гидрологии . 480 (1): 33–45. Бибкод : 2013JHyd..480...33R. doi :10.1016/j.jгидрол.2012.12.004.
10. Эверитт, Б.С. (2002). Кембриджский статистический словарь (2-е изд.). ЧАШКА. п. 78. ИСБН 978-0-521-81099-9.
11. Казелла, Жорж (2002). Статистический вывод (Второе изд.). Пасифик Гроув, Калифорния: Даксбери/Томсон Лиринг. п. 556. ИСБН 9788131503942.
12. Квалсет, Таральд О. (1985). «Предупреждение о R2». Американский статистик . 39 (4): 279–285. дои : 10.2307/2683704. JSTOR  2683704.
13. «Линейная регрессия — MATLAB и Simulink». www.mathworks.com .
14. https://www.utstat.toronto.edu/~brunner/books/LinearModelsWithR.pdf
15. Раджу, Намбери С.; Билгич, Рейхан; Эдвардс, Джек Э.; Флир, Пол Ф. (1997). «Обзор методологии: оценка генеральной и перекрестной достоверности, а также использование равных весов в прогнозировании». Прикладные психологические измерения . 21 (4): 291–305. дои : 10.1177/01466216970214001. ISSN  0146-6216. S2CID  122308344.
16. Мордехай Иезекииль (1930), Методы корреляционного анализа , Wiley , Wikidata  Q120123877, стр. 208-211.
17. Инь, Пин; Фань, Ситао (январь 2001 г.). «Оценка усадки R 2 в множественной регрессии: сравнение различных аналитических методов» (PDF) . Журнал экспериментального образования . 69 (2): 203–224. дои : 10.1080/00220970109600656. ISSN  0022-0973. S2CID  121614674.
18. Предполагая, что параметры p + 1 оценены
19. Ши, Гвовен (1 апреля 2008 г.). «Улучшенная оценка сокращения квадрата коэффициента множественной корреляции и квадрата коэффициента перекрестной достоверности». Организационные методы исследования . 11 (2): 387–407. дои : 10.1177/1094428106292901. ISSN  1094-4281. S2CID  55098407.
20. Олкин, Ингрэм; Пратт, Джон В. (март 1958 г.). «Непредвзятая оценка некоторых коэффициентов корреляции». Анналы математической статистики . 29 (1): 201–211. дои : 10.1214/aoms/1177706717 . ISSN  0003-4851.
21. Карч, Джулиан (29 сентября 2020 г.). «Улучшение скорректированного R-квадрата». Коллабра: Психология . 6 (45). дои : 10.1525/collabra.343 . hdl : 1887/3161248 . ISSN  2474-7394.
22. Ричард Андерсон-Спречер, «Сравнение моделей и R2», Американский статистик , том 48, выпуск 2, 1994, стр. 113–117.
23. Nagelkerke, NJD (сентябрь 1991 г.). «Примечание к общему определению коэффициента детерминации» (PDF) . Биометрика . 78 (3): 691–692. дои : 10.1093/biomet/78.3.691. JSTOR  2337038.
24. «Регрессия - R реализация коэффициента частичной детерминации» . Крест проверен .
25. Хорнвег, Виктор (2018). «Часть II: О сохранении фиксированных параметров». Наука: Подчинение . Хорнвег Пресс. ISBN 978-90-829188-0-9.
26. Кокс, Д.Д.; Снелл, Э.Дж. (1989). Анализ двоичных данных (2-е изд.). Чепмен и Холл.
27. Маги, Л. (1990). « Измерения R ² на основе критериев совместной значимости Вальда и отношения правдоподобия». Американский статистик . 44 (3): 250–3. дои : 10.1080/00031305.1990.10475731.
28. Нагелькерке, Нико JD (1992). Оценка максимального правдоподобия функциональных связей, Pays-Bas . Конспект лекций по статистике. Том. 69. ИСБН 978-0-387-97721-8.
29. Веб-страница OriginLab, http://www.originlab.com/doc/Origin-Help/LR-Algorithm. Проверено 9 февраля 2016 г.
30. Райт, Сьюэлл (январь 1921 г.). «Корреляция и причинно-следственная связь». Журнал сельскохозяйственных исследований . 20 : 557–585.

дальнейшее чтение

• Гуджарати, Дамодар Н .; Портер, Дон К. (2009). Основная эконометрика (Пятое изд.). Нью-Йорк: МакГроу-Хилл/Ирвин. стр. 73–78. ISBN 978-0-07-337577-9.
• Хьюз, Энн; Гравойг, Деннис (1971). Статистика: основа анализа. Чтение: Аддисон-Уэсли. стр. 344–348. ISBN 0-201-03021-7.
• Кмента, Ян (1986). Элементы эконометрики (второе изд.). Нью-Йорк: Макмиллан. стр. 240–243. ISBN 978-0-02-365070-3.
• Льюис-Бек, Майкл С .; Скалабан, Эндрю (1990). « R -квадрат: немного откровенного разговора». Политический анализ . 2 : 153–171. дои : 10.1093/пан/2.1.153. JSTOR  23317769.
• Чикко, Давиде; Уорренс, Маттейс Дж.; Юрман, Джузеппе (2021). «Коэффициент детерминации R-квадрат более информативен, чем SMAPE, MAE, MAPE, MSE и RMSE при оценке регрессионного анализа». PeerJ Информатика . 7 (e623): e623. дои : 10.7717/peerj-cs.623 . ПМЦ  8279135 . ПМИД  34307865.