Закон Пашена

Физический закон об электрическом разряде в газах

Кривые Пашена, полученные для гелия, неона, аргона, водорода и азота, с использованием выражения для напряжения пробоя как функции параметров A, B, которые интерполируют первый коэффициент Таунсенда . ^[1]

Закон Пашена — это уравнение, которое определяет напряжение пробоя , то есть напряжение, необходимое для возникновения разряда или электрической дуги , между двумя электродами в газе в зависимости от давления и длины зазора. ^{[2] [3]} Он назван в честь Фридриха Пашена , который открыл его эмпирическим путем в 1889 году. ^[4]

Пашен изучал напряжение пробоя различных газов между параллельными металлическими пластинами при изменении давления газа и расстояния между ними:

• При постоянной длине зазора напряжение, необходимое для образования дуги в зазоре, уменьшалось по мере снижения давления, а затем постепенно увеличивалось, превышая свое первоначальное значение.
• При постоянном давлении напряжение, необходимое для возникновения дуги, уменьшалось по мере уменьшения размера зазора, но только до определенной точки. По мере дальнейшего уменьшения зазора напряжение, необходимое для возникновения дуги, начинало расти и снова превышало свое первоначальное значение.

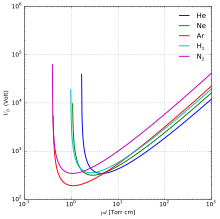
Для данного газа напряжение является функцией только произведения давления и длины зазора. ^{[2] [3]} Найденная им кривая зависимости напряжения от произведения давления на длину зазора (справа) называется кривой Пашена . Он нашел уравнение, которое соответствует этим кривым, и которое теперь называется законом Пашена. ^[3]

При более высоких давлениях и длинах зазоров напряжение пробоя приблизительно пропорционально произведению давления и длины зазора, и для обозначения этого более простого соотношения иногда используется термин «закон Пашена». ^[5] Однако это верно лишь приблизительно и в ограниченном диапазоне кривой.

кривая Пашена

Ранние экспериментаторы с вакуумом обнаружили довольно удивительное поведение. Дуга иногда возникала на длинном нерегулярном пути, а не на минимальном расстоянии между электродами. Например, в воздухе при давлении в одну атмосферу расстояние для минимального пробивного напряжения составляет около 7,5 мкм. Напряжение, необходимое для возникновения дуги на этом расстоянии, составляет 327 В, что недостаточно для зажигания дуги для зазоров, которые либо шире, либо уже. Для зазора в 3,5 мкм необходимое напряжение составляет 533 В, почти вдвое больше. Если бы было подано 500 В, этого было бы недостаточно для возникновения дуги на расстоянии 2,85 мкм, но дуга возникла бы на расстоянии 7,5 мкм.

Пашен обнаружил, что напряжение пробоя описывается уравнением ^[1]

${\displaystyle V_{\text{B}}={\frac {Bpd}{\ln(Apd)-\ln \left[\ln \left(1+{\frac {1}{\gamma _{\text{se}}}}\right)\right]}}}$

где - напряжение пробоя в вольтах , - давление в паскалях , - расстояние между электродами в метрах , - коэффициент вторичной электронной эмиссии (количество вторичных электронов, образующихся на один падающий положительный ион), - ионизация насыщения в газе при определенном значении ( электрическое поле /давление), и связана с энергиями возбуждения и ионизации. ${\displaystyle V_{\text{B}}}$ ${\displaystyle p}$ ${\displaystyle d}$ ${\displaystyle \gamma _{\text{se}}}$ ${\displaystyle A}$ ${\displaystyle E/p}$ ${\displaystyle B}$

Константы и интерполируют первый коэффициент Таунсенда . Они определяются экспериментально и оказываются примерно постоянными в ограниченном диапазоне для любого заданного газа. Например, воздух с в диапазоне от 450 до 7500 В/(кПа·см),  = 112,50 (кПа·см) ⁻¹ и = 2737,50 В/(кПа·см). ^[6] ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \alpha =Ape^{-Bp/E}}$ ${\displaystyle E/p}$ ${\displaystyle E/p}$ ${\displaystyle A}$ ${\displaystyle B}$

График этого уравнения — кривая Пашена. Дифференцируя ее по и приравнивая производную к нулю, можно найти минимальное напряжение. Это дает ${\displaystyle pd}$

${\displaystyle pd={\frac {e\cdot \ln \left(1+{\frac {1}{{\mathit {\gamma }}_{se}}}\right)}{A}}}$

и предсказывает возникновение минимального пробивного напряжения для  = 7,5×10−6 ^м  ·атм. Это 327 В в воздухе при стандартном атмосферном давлении на расстоянии 7,5 мкм. ${\displaystyle pd}$

Состав газа определяет как минимальное напряжение дуги, так и расстояние, на котором оно возникает. Для аргона минимальное напряжение дуги составляет 137 В при большем 12 мкм. Для диоксида серы минимальное напряжение дуги составляет 457 В всего лишь при 4,4 мкм.

Длинные промежутки

Для воздуха при стандартных условиях температуры и давления (СТП) напряжение, необходимое для образования дуги в зазоре длиной 1 м, составляет около 3,4 МВ. ^[7] Таким образом, напряженность электрического поля для этого зазора составляет 3,4 МВ/м.

Электрическое поле, необходимое для дуги через зазор с минимальным напряжением, намного больше, чем то, что необходимо для дуги в зазоре в один метр. При больших зазорах (или большом pd) закон Пашена, как известно, не выполняется. Критерий Мика для пробоя обычно используется для больших зазоров. ^[8] Он учитывает неоднородность электрического поля и образование стримеров из-за накопления заряда внутри зазора, которое может происходить на больших расстояниях. Для зазора 7,5 мкм напряжение дуги составляет 327 В, что составляет 43 МВ/м. Это примерно в 14 раз больше, чем напряженность поля для зазора 1,5 метра. Явление хорошо проверено экспериментально и называется минимумом Пашена.

Уравнение теряет точность для зазоров менее 10 мкм в воздухе при одной атмосфере ^[9] и неправильно предсказывает бесконечное напряжение дуги при зазоре около 2,7 мкм. Напряжение пробоя также может отличаться от предсказания кривой Пашена для очень малых зазоров между электродами, когда полевая эмиссия с поверхности катода становится важной.

Физический механизм

Средний свободный пробег молекулы в газе — это среднее расстояние между ее столкновениями с другими молекулами. Оно обратно пропорционально давлению газа при постоянной температуре. В воздухе при СТП средний свободный пробег молекул составляет около 96 нм. Поскольку электроны намного меньше, их среднее расстояние между столкновениями с молекулами примерно в 5,6 раза больше, или около 0,5 мкм. Это существенная часть расстояния между электродами в 7,5 мкм для минимального напряжения дуги. Если электрон находится в электрическом поле 43 МВ/м, он будет ускоряться и приобретать 21,5  эВ энергии за 0,5 мкм перемещения в направлении поля. Первая энергия ионизации, необходимая для выбивания электрона из молекулы азота , составляет около 15,6 эВ. Ускоренный электрон приобретет более чем достаточно энергии для ионизации молекулы азота. Этот освобожденный электрон, в свою очередь, будет ускоряться, что приведет к другому столкновению. Затем цепная реакция приводит к лавинному пробою , и из каскада высвобождающихся электронов возникает дуга. ^[10]

Больше столкновений будет происходить на пути электрона между электродами в газе с более высоким давлением. Когда произведение давления на зазор велико, электрон будет сталкиваться со многими различными молекулами газа по мере своего перемещения от катода к аноду. Каждое из столкновений рандомизирует направление электрона, поэтому электрон не всегда ускоряется электрическим полем — иногда он движется обратно к катоду и замедляется полем. ${\displaystyle pd}$

Столкновения уменьшают энергию электрона и затрудняют ионизацию молекулы. Потери энергии от большего числа столкновений требуют большего напряжения, чтобы электроны накопили достаточно энергии для ионизации многих молекул газа, что необходимо для лавинного пробоя .

С левой стороны минимума Пашена произведение мало. Длина свободного пробега электронов может стать больше по сравнению с зазором между электродами. В этом случае электроны могут получить большое количество энергии, но иметь меньше ионизирующих столкновений. Поэтому требуется большее напряжение, чтобы обеспечить ионизацию достаточного количества молекул газа для начала лавины. ${\displaystyle pd}$

Вывод

Основы

Для расчета напряжения пробоя предполагается однородное электрическое поле. Это имеет место в установке плоскопараллельного конденсатора . Электроды могут иметь расстояние . Катод расположен в точке . ${\displaystyle d}$ ${\displaystyle x=0}$

Чтобы получить ударную ионизацию , энергия электронов должна стать больше энергии ионизации атомов газа между пластинами. На длину пути произойдет несколько ионизаций. известен как первый коэффициент Таунсенда, поскольку был введен Таунсендом. ^[11] Увеличение тока электронов можно описать для предполагаемой установки как ${\displaystyle E_{e}}$ ${\displaystyle E_{\text{I}}}$ ${\displaystyle x}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha }$ ${\displaystyle \Gamma _{e}}$

(Таким образом, число свободных электронов на аноде равно числу свободных электронов на катоде, умноженных на ударную ионизацию. Чем больше и/или , тем больше создается свободных электронов.) ${\displaystyle d}$ ${\displaystyle \alpha }$

Число созданных электронов равно

Пренебрегая возможными многократными ионизациями одного и того же атома, число созданных ионов равно числу созданных электронов:

${\displaystyle \Gamma _{i}}$— это ионный ток. Чтобы поддерживать разряд, на поверхности катода должны создаваться свободные электроны. Это возможно, поскольку ионы, ударяющиеся о катод, высвобождают вторичные электроны при ударе. (При очень больших приложенных напряжениях может также происходить полевая эмиссия электронов .) Без полевой эмиссии мы можем записать

где — среднее число сгенерированных вторичных электронов на ион. Это также известно как второй коэффициент Таунсенда. Предполагая, что , получаем соотношение между коэффициентами Таунсенда, подставляя ( 4 ) в ( 3 ) и преобразуя: ${\displaystyle \gamma }$ ${\displaystyle \Gamma _{i}(d)=0}$

Ударная ионизация

Каково количество ? Количество ионизации зависит от вероятности того, что электрон попадет в молекулу газа. Эта вероятность представляет собой отношение площади поперечного сечения столкновения электрона и иона к общей площади , доступной для пролета электрона: ${\displaystyle \alpha }$ ${\displaystyle P}$ ${\displaystyle \sigma }$ ${\displaystyle A}$

Как выражено во второй части уравнения, вероятность также можно выразить как отношение пути, пройденного электроном, к средней длине свободного пробега (расстоянию, на котором происходит другое столкновение). ${\displaystyle x}$ ${\displaystyle \lambda }$

Визуализация поперечного сечения : Если центр частицы b проникает в синий круг, происходит столкновение с частицей a . Таким образом, площадь круга является поперечным сечением, а его радиус - суммой радиусов частиц. ${\displaystyle \sigma }$ ${\displaystyle r}$

${\displaystyle N}$это число молекул, которые могут ударить электроны. Его можно рассчитать с помощью уравнения состояния идеального газа

( : давление, : объем, : постоянная Больцмана , : температура) ${\displaystyle p}$ ${\displaystyle V}$ ${\displaystyle k_{B}}$ ${\displaystyle T}$

Прилагаемый рисунок иллюстрирует, что . Поскольку радиусом электрона можно пренебречь по сравнению с радиусом иона, он упрощается до . Используя это соотношение, подставляя ( 7 ) в ( 6 ) и преобразуя к получаем ${\displaystyle \sigma =\pi (r_{a}+r_{b})^{2}}$ ${\displaystyle r_{I}}$ ${\displaystyle \sigma =\pi r_{I}^{2}}$ ${\displaystyle \lambda }$

где этот фактор был введен только для лучшего обзора. ${\displaystyle L}$

Изменение тока еще не столкнувшихся электронов в каждой точке пути можно выразить как ${\displaystyle x}$

Это дифференциальное уравнение легко решается:

Вероятность того, что (в точке еще не произошло столкновения ), равна ${\displaystyle \lambda >x}$ ${\displaystyle x}$

Согласно его определению, это число ионизаций на единицу длины пути и, следовательно, отношение вероятности того, что не произошло ни одного столкновения на длине свободного пробега ионов, к длине свободного пробега электронов: ${\displaystyle \alpha }$

При этом считалось, что энергия , которую может получить заряженная частица между столкновениями, зависит от напряженности электрического поля и заряда : ${\displaystyle E}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle Q}$

Напряжение пробоя

Для плоского конденсатора имеем , где - приложенное напряжение. Поскольку предполагалась единичная ионизация, то элементарный заряд . Теперь мы можем подставить ( 13 ) и ( 8 ) в ( 12 ) и получить ${\displaystyle {\mathcal {E}}={\frac {U}{d}}}$ ${\displaystyle U}$ ${\displaystyle Q}$ ${\displaystyle e}$

Подставляя это в (5) и преобразуя к, мы получаем закон Пашена для напряжения пробоя , который впервые был исследован Пашеном в ^[4] и формула которого была впервые выведена Таунсендом в ^[12] ${\displaystyle U}$ ${\displaystyle U_{\mathrm {breakdown} }}$

с ${\textstyle L={\frac {\pi r_{I}^{2}}{k_{B}T}}}$

Плазменное зажигание

Плазменное зажигание в определении Таунсенда ( разряд Таунсенда ) — это самоподдерживающийся разряд, независимый от внешнего источника свободных электронов. Это означает, что электроны от катода могут достигать анода на расстоянии и ионизировать по пути хотя бы один атом. Так что согласно определению должно выполняться это соотношение: ${\displaystyle d}$ ${\displaystyle \alpha }$

Если вместо ( 5 ) использовать, то для напряжения пробоя получим ${\displaystyle \alpha d=1}$

Выводы, обоснованность

Закон Пашена требует, чтобы:

• На катоде ( ) уже есть свободные электроны , которые можно ускорить, чтобы вызвать ударную ионизацию. Такие так называемые затравочные электроны могут быть созданы путем ионизации естественной радиоактивностью или космическими лучами. ${\displaystyle \Gamma _{e}(x=0)\neq 0}$
• Создание дополнительных свободных электронов достигается только посредством ударной ионизации. Таким образом, закон Пашена недействителен, если есть внешние источники электронов. Это может быть, например, источник света, создающий вторичные электроны посредством фотоэлектрического эффекта . Это необходимо учитывать в экспериментах.
• Каждый ионизированный атом приводит только к одному свободному электрону. Однако на практике всегда происходит многократная ионизация.
• Свободные электроны на поверхности катода создаются ударяющимися ионами. Проблема в том, что количество таким образом созданных электронов сильно зависит от материала катода, его поверхности ( шероховатости , примесей) и условий окружающей среды (температуры, влажности и т. д.). Экспериментальное, воспроизводимое определение фактора поэтому практически невозможно. ${\displaystyle \gamma }$
• Электрическое поле однородно.

Эффекты с различными газами

Разные газы будут иметь разные средние свободные пробеги для молекул и электронов. Это происходит потому, что разные молекулы имеют сечения ионизации, то есть разные эффективные диаметры. Благородные газы, такие как гелий и аргон, являются одноатомными , что затрудняет их ионизацию и, как правило, они имеют меньшие эффективные диаметры. Это дает им большие средние свободные пробеги.

Потенциалы ионизации различаются между молекулами, как и скорость, с которой они возвращают себе электроны после того, как их выбили с орбиты. Все три эффекта изменяют количество столкновений, необходимых для экспоненциального роста свободных электронов. Эти свободные электроны необходимы для возникновения дуги.

Смотрите также

• Атмосферное давление
• Напряжение пробоя
• Диэлектрическая прочность
• разряд Таунсенда

Ссылки

1. Либерман, Майкл А.; Лихтенберг, Аллан Дж. (2005). Принципы плазменных разрядов и обработки материалов (2-е изд.). Хобокен, Нью-Джерси: Wiley-Interscience. 546. ISBN 978-0471005773. OCLC  59760348.
2. "Закон Пашена". Онлайн-словарь Merriam-Webster . Merriam-Webster, Inc. 2013. Получено 9 июня 2017 г.
3. Wadhwa, CL (2007). High Voltage Engineering (2-е изд.). New Age International. стр. 10–12. ISBN 978-8122418590.
4. Пашен, Ф. (1889). «Über die zum Funkenübergang in Luft, Wasserstoff und Kohlensäure bei verschiedenen Drucken erforderliche Potentialdifferenz». Аннален дер Физик . 273 (5): 69–96. Бибкод : 1889АнП...273...69П. дои : 10.1002/andp.18892730505. hdl : 2027/uc1.$b624756 .
5. Граф, Рудольф Ф. (1999). Современный словарь электроники (7-е изд.). Newnes. стр. 542. ISBN 978-0750698665.
6. Хусейн, Э.; Нема, Р. (август 1982 г.). «Анализ кривых Пашена для воздуха, N2 и SF6 с использованием уравнения разложения Таунсенда». Труды IEEE по электроизоляции . EI-17 (4): 350–353. doi :10.1109/TEI.1982.298506. S2CID  35169293.
7. Типлер, Пол (1989). Колледж физики . Нью-Йорк, Нью-Йорк: Worth Publishers. стр. 467. ISBN 978-0879012687.
8. Meek, JM (1940-04-15). "Теория искрового разряда". Physical Review . 57 (8). Американское физическое общество: 722–728. Bibcode : 1940PhRv...57..722M. doi : 10.1103/PhysRev.57.722.
9. Hourdakis, Emmanouel; Simonds, Brian J. & Zimmerman, Neil M. (2006). "Субмикронный конденсатор для измерения пробивного напряжения в воздухе". Rev. Sci. Instrum . 77 (3): 034702–034702–4. Bibcode : 2006RScI...77c4702H. doi : 10.1063/1.2185149.
10. Электрические разряды. Как работают искра, тлеющий разряд и дуга.
11. Таунсенд, Дж. С. (1910). «17. Проводимость между параллельными пластинами, когда положительные и отрицательные ионы генерируют другие при столкновениях». Теория ионизации газов при столкновениях. Констебль.
12. Таунсенд, Дж. С. (1915). "227. Потенциал искрообразования как функция числа молекул между параллельными пластинами". Электричество в газах. Clarendon Press. OCLC  4294747.

Внешние ссылки

• Пределы электрического пробоя для МЭМС
• Справочник высоковольтного экспериментатора Архивировано 2011-10-16 в Wayback Machine
• Калькулятор закона Пашена
• Напряжение пробоя в зависимости от давления
• Электрический пробой газов низкого давления
• Электрические разряды
• Зависимость структуры плазмы от давления при микроволновом пробое газа на частоте 110 ГГц