
В инженерии и материаловедении кривая напряжения-деформации для материала показывает соотношение между напряжением и деформацией . Она получается путем постепенного приложения нагрузки к испытательному образцу и измерения деформации , из которой можно определить напряжение и деформацию (см. испытание на растяжение ). Эти кривые показывают многие свойства материала , такие как модуль Юнга , предел текучести и предел прочности на растяжение .
Вообще говоря, кривые, представляющие связь между напряжением и деформацией в любой форме деформации, можно рассматривать как кривые напряжение-деформация. Напряжение и деформация могут быть нормальными, сдвиговыми или смешанными, а также могут быть одноосными, двухосными или многоосными, даже изменяться со временем. Форма деформации может быть сжатием , растяжением, кручением , вращением и т. д. Если не указано иное, кривая напряжение-деформация относится к связи между осевым нормальным напряжением и осевой нормальной деформацией материалов, измеренных при испытании на растяжение.
Схематическая диаграмма для кривой напряжение-деформация низкоуглеродистой стали при комнатной температуре показана на рисунке 1. Существует несколько стадий, показывающих различное поведение, что предполагает различные механические свойства . Для ясности, материалы могут пропускать одну или несколько стадий, показанных на рисунке 1, или иметь совершенно разные стадии.
Первая стадия — это линейная упругая область. Напряжение пропорционально деформации, то есть подчиняется общему закону Гука , а наклон — модулю Юнга . В этой области материал претерпевает только упругую деформацию. Конец стадии — это точка начала пластической деформации. Составляющая напряжения этой точки определяется как предел текучести (или верхний предел текучести, сокращенно UYP).
Вторая стадия — область деформационного упрочнения . Эта область начинается, когда напряжение выходит за пределы предела текучести, достигая максимума в точке предельной прочности, которая является максимальным напряжением, которое может быть выдержано, и называется пределом прочности на растяжение (UTS). В этой области напряжение в основном увеличивается по мере удлинения материала, за исключением того, что для некоторых материалов, таких как сталь, в начале есть почти плоская область. Напряжение плоской области определяется как нижний предел текучести (LYP) и является результатом образования и распространения полос Людерса . Явно, неоднородная пластическая деформация образует полосы при верхнем пределе текучести, и эти полосы, несущие деформацию, распространяются вдоль образца при нижнем пределе текучести. После того, как образец снова равномерно деформируется, увеличение напряжения с прогрессом растяжения является результатом рабочего упрочнения, то есть плотные дислокации, вызванные пластической деформацией, затрудняют дальнейшее движение дислокаций. Чтобы преодолеть эти препятствия, следует применить более высокое разрешенное напряжение сдвига . По мере накопления деформации рабочее упрочнение усиливается до тех пор, пока напряжение не достигнет предельной прочности на растяжение.
Третий этап — область шейки. Помимо предела прочности на растяжение, шейка образуется там, где локальная площадь поперечного сечения становится значительно меньше средней. Деформация шейки неоднородна и будет усиливаться, поскольку напряжение больше концентрируется на малом сечении. Такая положительная обратная связь приводит к быстрому развитию шейки и приводит к разрушению. Обратите внимание, что хотя сила натяжения уменьшается, упрочнение работой все еще продолжается, то есть истинное напряжение продолжает расти, но инженерное напряжение уменьшается, поскольку площадь сечения усадки не учитывается. Эта область заканчивается разрушением. После разрушения можно рассчитать процентное удлинение и уменьшение площади сечения.
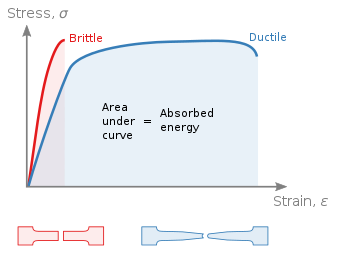
Можно выделить некоторые общие характеристики среди кривых напряжение-деформация различных групп материалов и на этой основе разделить материалы на две большие категории, а именно, пластичные материалы и хрупкие материалы. [1] : 51
Пластичные материалы, включая конструкционную сталь и многие другие металлы, характеризуются способностью к пластической деформации при нормальных температурах. [1] : 58 Например, низкоуглеродистая сталь обычно демонстрирует очень линейную зависимость напряжения от деформации вплоть до четко определенного предела текучести . Линейная часть кривой представляет собой упругую область, а наклон этой области представляет собой модуль упругости или модуль Юнга . Пластическое течение начинается в верхнем пределе текучести и продолжается в нижнем пределе текучести.
Появление верхнего предела текучести связано с закреплением дислокаций в системе. Остаточная деформация возникает, когда дислокации вынуждены пройти точки закрепления. Первоначально эта остаточная деформация неравномерно распределена по образцу. Во время этого процесса дислокации выходят из атмосфер Коттрелла внутри материала. Образующиеся полосы скольжения появляются в нижнем пределе текучести и распространяются вдоль длины калибра при постоянном напряжении до тех пор, пока не будет достигнута деформация Людерса, и деформация не станет однородной.
За пределами деформации Людерса напряжение увеличивается из-за деформационного упрочнения , пока не достигнет предельного напряжения растяжения . На этом этапе площадь поперечного сечения равномерно уменьшается по длине калибра из-за несжимаемости пластического течения (а не из-за эффекта Пуассона , который является упругим явлением). Затем начинается процесс образования шейки , который заканчивается разрушением типа «чашка и конус», характерным для пластичных материалов.
Появление шейки в пластичных материалах связано с геометрической нестабильностью в системе. Из-за естественной неоднородности материала часто встречаются области с небольшими включениями или пористостью внутри материала или на его поверхности, где будет концентрироваться деформация, что приведет к локальному уменьшению площади поперечного сечения. При деформации, меньшей предельной деформации растяжения, увеличение скорости упрочнения в этой области будет больше, чем скорость уменьшения площади, тем самым делая эту область более трудной для деформации, чем другие, так что нестабильность будет устранена, т. е. материал увеличит однородность до достижения предельной деформации. Однако за пределами этого скорость упрочнения будет уменьшаться, так что область с меньшей площадью будет слабее соседних областей, поэтому уменьшение площади будет концентрироваться в этой области, и шейка будет становиться все более и более выраженной до разрушения. После того, как шейка образовалась в материале, дальнейшая пластическая деформация концентрируется в шейке, в то время как остальная часть материала претерпевает упругое сжатие из-за уменьшения силы растяжения.
Кривую зависимости деформации от напряжения для пластичного материала можно аппроксимировать с помощью уравнения Рамберга–Осгуда . [2] Это уравнение легко реализовать, для него требуются только предел текучести материала, предел прочности, модуль упругости и процентное удлинение.

Материалы, которые являются одновременно прочными и пластичными, классифицируются как вязкие . Вязкость — это свойство материала, определяемое как площадь под кривой зависимости деформации от напряжения.
Прочность можно определить путем интегрирования кривой напряжения-деформации. [3] Это энергия механической деформации на единицу объема до разрушения. Явное математическое описание: [4] где
Хрупкие материалы, к которым относятся чугун, стекло и камень, характеризуются тем, что разрыв происходит без какого-либо заметного предварительного изменения скорости удлинения [1] : 59 иногда они разрушаются до того, как достигнут текучести.
Хрупкие материалы, такие как бетон или углеродное волокно, не имеют четко определенного предела текучести и не упрочняются деформацией. Поэтому предел прочности и прочность на разрыв одинаковы. Типичные хрупкие материалы, такие как стекло, не демонстрируют никакой пластической деформации , но разрушаются, пока деформация является упругой . Одной из характеристик хрупкого разрушения является то, что две сломанные части могут быть повторно собраны для получения той же формы, что и исходный компонент, поскольку не будет образования шейки, как в случае пластичных материалов. Типичная кривая напряжения-деформации для хрупкого материала будет линейной. Для некоторых материалов, таких как бетон , предел прочности на растяжение пренебрежимо мал по сравнению с пределом прочности на сжатие, и для многих инженерных приложений он предполагается равным нулю. Стекловолокно имеет предел прочности на растяжение выше, чем сталь, но объемное стекло обычно нет. Это связано с коэффициентом интенсивности напряжений , связанным с дефектами в материале. По мере увеличения размера образца ожидаемый размер самого большого дефекта также растет.