Круговая диаграмма

Граф пересечения хордовой диаграммы

Окружность с пятью хордами и соответствующий ей график окружности.

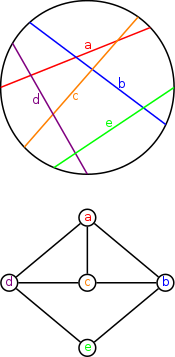
В теории графов круговой граф — это граф пересечений хордовой диаграммы . То есть это неориентированный граф , вершины которого могут быть сопоставлены с конечной системой хорд окружности таким образом , что две вершины являются смежными тогда и только тогда, когда соответствующие хорды пересекают друг друга.

Алгоритмическая сложность

После более ранних алгоритмов полиномиального времени ^[1] Джоан и др. (2013) представили алгоритм распознавания круговых графов за почти линейное время. Их метод медленнее линейного на коэффициент обратной функции Аккермана и основан на лексикографическом поиске в ширину . Время выполнения достигается за счет метода поддержания разбиения графа на части по мере добавления вершин, используемого в качестве подпрограммы в алгоритме. ^[2]

Ряд других задач, которые являются NP-полными на общих графах, имеют алгоритмы полиномиального времени, когда ограничиваются круговыми графами. Например, Клокс (1996) показал, что ширина дерева кругового графа может быть определена, и построено оптимальное разложение дерева за время O( n ³ ). Кроме того, минимальное заполнение (то есть хордовый граф с минимальным количеством ребер, содержащий заданный круговой граф в качестве подграфа) может быть найдено за время O( n ³ ). ^[3] Тискин (2010) показал, что максимальная клика кругового графа может быть найдена за время O( n log ² n ), в то время как Нэш и Грегг (2010) показали, что максимальное независимое множество невзвешенного кругового графа может быть найдено за время O( n min{ d , α }), где d — параметр графа, известный как его плотность, а α — число независимости кругового графа.

Однако существуют также задачи, которые остаются NP-полными, если ограничиться круговыми графами. К ним относятся задачи минимального доминирующего множества , минимального связного доминирующего множества и минимального общего доминирующего множества. ^[4]

Хроматическое число

Хорды, образующие 220-вершинный 5-хроматический круговой граф без треугольников Агеева (1996), изображенный как последовательность линий на гиперболической плоскости .

Хроматическое число кругового графа — это минимальное количество цветов, которое может быть использовано для раскраски его хорд так, чтобы никакие две пересекающиеся хорды не имели одного цвета. Поскольку возможно сформировать круговые графы, в которых произвольно большие наборы хорд пересекаются друг с другом, хроматическое число кругового графа может быть произвольно большим, и определение хроматического числа кругового графа является NP-полной задачей. ^[5] Остается NP-полной задача проверки того, можно ли раскрасить круговой граф четырьмя цветами. ^[6] Унгер (1992) утверждал, что нахождение раскраски тремя цветами может быть выполнено за полиномиальное время , но его описание этого результата опускает многие детали. ^[7]

Несколько авторов исследовали проблемы раскраски ограниченных подклассов круговых графов с помощью небольшого количества цветов. В частности, для круговых графов, в которых нет наборов из k или более хорд, пересекающих друг друга, можно раскрасить граф всего лишь несколькими цветами. Одним из способов утверждения этого является то, что круговые графы являются -ограниченными . ^[8] В частном случае, когда k  = 3 (то есть для круговых графов без треугольников ), хроматическое число не превышает пяти, и это ограничено: все круговые графы без треугольников можно раскрасить пятью цветами, и существуют круговые графы без треугольников, которым требуется пять цветов. ^[9] Если круговой граф имеет обхват не менее пяти (то есть он не содержит треугольников и не имеет циклов с четырьмя вершинами), его можно раскрасить не более чем тремя цветами. ^[10] Задача раскраски квадратных графов без треугольников эквивалентна задаче представления квадратных графов в виде изометрических подграфов декартовых произведений деревьев ; В этом соответствии количество цветов в раскраске соответствует количеству деревьев в представлении продукта. ^[11] ${\displaystyle 7k^{2}}$ ${\displaystyle \chi }$

Приложения

Круговые графы возникают в физическом проектировании СБИС как абстрактное представление для особого случая маршрутизации проводов , известного как «маршрутизация двухконтактной распределительной коробки». В этом случае область маршрутизации представляет собой прямоугольник, все сети являются двухконтактными, а клеммы размещаются по периметру прямоугольника. Легко видеть, что граф пересечения этих сетей представляет собой круговой граф. ^[12] Среди целей этапа маршрутизации проводов — гарантировать, что различные сети остаются электрически разъединенными, а их потенциально пересекающиеся части должны быть размещены в разных проводящих слоях. Поэтому круговые графы охватывают различные аспекты этой проблемы маршрутизации.

Раскраски круговых графов также могут быть использованы для поиска книжных вложений произвольных графов: если вершины данного графа G расположены на окружности, а ребра G образуют хорды окружности, то граф пересечений этих хорд является круговым графом, а раскраски этого кругового графа эквивалентны книжным вложениям, которые соблюдают заданную круговую компоновку. В этой эквивалентности количество цветов в раскраске соответствует количеству страниц в книжном вложении. ^[6]

Связанные классы графов

Интервальная система с пятью интервалами и соответствующим графом перекрытия.

Граф является круговым графом тогда и только тогда, когда он является графом перекрытия набора интервалов на линии. Это граф, в котором вершины соответствуют интервалам, а две вершины соединены ребром, если два интервала перекрываются, и ни один из них не содержит другой.

Граф пересечения множества интервалов на прямой называется графом интервалов .

Графы строк , графы пересечений кривых на плоскости, включают в себя графы окружностей как частный случай.

Каждый дистанционно-наследуемый граф является круговым графом, как и каждый граф перестановок и каждый граф безразличия . Каждый внешнепланарный граф также является круговым графом. ^[13]

Круговые графы обобщаются с помощью многоугольно-круговых графов , графов пересечения многоугольников, вписанных в одну и ту же окружность. ^[14]

Примечания

1. Габор, Суповит и Хсу (1989); Спинрад (1994)
2. Джоан и др. (2013).
3. Клокс, Кратч и Вонг (1998).
4. Кейл (1993)
5. Гарей и др. (1980).
6. Unger (1988).
7. Унгер (1992).
8. Дэвис и Маккарти (2021). Более ранние оценки см. в Černy (2007), Gyárfás (1985), Kostochka (1988) и Kostochka & Kratochvíl (1997).
9. См. Косточку (1988) для верхней границы и Агеева (1996) для соответствующей нижней границы. Карапетян (1984) и Дьярфас и Лехель (1985) дают более ранние более слабые границы для той же проблемы.
10. Агеев (1999).
11. Бандельт, Чепой и Эппштейн (2010).
12. Навид Шервани, «Алгоритмы для автоматизации физического проектирования СБИС»
13. Вессель и Пёшель (1985); Унгер (1988).
14. "Круговой граф", Информационная система по классам графов и их включениям

Ссылки

• Агеев, А.А. (1996), "Круговой граф без треугольников с хроматическим числом 5", Дискретная математика , 152 (1–3): 295–298, doi : 10.1016/0012-365X(95)00349-2.
• Агеев, А.А. (1999), «Любой круговой граф с обхватом не менее 5 является 3-раскрашиваемым», Дискретная математика , 195 (1–3): 229–233, doi : 10.1016/S0012-365X(98)00192-7.
• Бандельт, Х.-Й.; Чепои, В.; Эппштейн, Д. (2010), «Комбинаторика и геометрия конечных и бесконечных квадратных графов», SIAM Journal on Discrete Mathematics , 24 (4): 1399–1440, arXiv : 0905.4537 , doi : 10.1137/090760301, S2CID  10788524.
• Черны, Якуб (2007), «Раскрашивание круговых графов», Electronic Notes in Discrete Mathematics , 29 : 357–361, doi :10.1016/j.endm.2007.07.072.
• Дэвис, Джеймс; Маккарти, Роуз (2021), «Круговые графы квадратично ограничены по χ», Бюллетень Лондонского математического общества , 53 (3): 673–679, arXiv : 1905.11578 , doi : 10.1112/blms.12447, MR  4275079, S2CID  167217723.
• Габор, Чаба П.; Суповит, Кеннет Дж.; Хсу, Вэнь-Лянь (июль 1989 г.), «Распознавание круговых графов за полиномиальное время», Журнал ACM , 36 (3): 435–473, doi : 10.1145/65950.65951
• Гари, MR ; Джонсон, DS ; Миллер, GL ; Пападимитриу, C. (1980), «Сложность раскраски дуг окружностей и хорд», Журнал SIAM по алгебраическим и дискретным методам , 1 (2): 216–227, doi :10.1137/0601025
• Джоан, Эмерик; Пол, Кристоф; Теддер, Марк; Корнейл, Дерек (март 2013 г.), «Практическое и эффективное распознавание круговых графов», Algorithmica , 69 (4): 759–788, arXiv : 1104.3284 , doi : 10.1007/s00453-013-9745-8
• Дьярфас, А. (1985), «О хроматическом числе кратных интервальных графов и графов перекрытия», Дискретная математика , 55 (2): 161–166, doi : 10.1016/0012-365X(85)90044-5. Цитируется по Агееву (1996).
• Gyárfás, A. ; Lehel, J. (1985), "Проблемы покрытия и раскраски для родственников интервалов", Discrete Mathematics , 55 (2): 167–180, doi : 10.1016/0012-365X(85)90045-7. Цитируется по Агееву (1996).
• Карапетян, А. (1984), О совершенных графах пересечения дуг и хорд , Кандидатская диссертация, Ин-т математики, Новосибирск. Цитируется по Агееву (1996).
• Кейл, Дж. Марк (1993), «Сложность задач доминирования в круговых графах», Дискретная прикладная математика , 42 (1): 51–63, doi : 10.1016/0166-218X(93)90178-Q.
• Клокс, Тон (1996), «Древовидная ширина круговых графов», Int. J. Found. Comput. Sci. , 7 (2): 111–120, doi :10.1142/S0129054196000099.
• Клокс, Т.; Кратч, Д.; Вонг, К.К. (1998), «Минимальное заполнение на круговых и дуговых графах», Журнал алгоритмов , 28 (2): 272–289, doi :10.1006/jagm.1998.0936.
• Косточка, А.В. (1988), «Верхние оценки хроматического числа графов», Труды Института математики , 10 : 204–226, MR  0945704. Цитируется по Агееву (1996).
• Косточка, А. В.; Кратохвил, Й. (1997), «Покрытие и раскраска многоугольно-круговых графов», Дискретная математика , 163 (1–3): 299–305, doi : 10.1016/S0012-365X(96)00344-5.
• Нэш, Николас; Грегг, Дэвид (2010), «Выходной чувствительный алгоритм для вычисления максимального независимого множества кругового графа», Information Processing Letters , 116 (16): 630–634, doi : 10.1016/j.ipl.2010.05.016, hdl : 10344/2228.
• Спинрад, Джереми (1994), «Распознавание круговых графов», Журнал алгоритмов , 16 (2): 264–282, doi :10.1006/jagm.1994.1012.
• Тискин, Александр (2010), «Быстрое умножение расстояний единичных матриц Монжа», Труды ACM-SIAM SODA 2010 , стр. 1287–1296.
• Унгер, Вальтер (1988), «О k -раскраске круговых графов», STACS 88: 5-й ежегодный симпозиум по теоретическим аспектам компьютерной науки, Бордо, Франция, 11–13 февраля 1988 г., Труды , Lecture Notes in Computer Science, т. 294, Берлин: Springer, стр. 61–72, doi :10.1007/BFb0035832.
• Унгер, Вальтер (1992), «Сложность раскраски круговых графов», STACS 92: 9-й ежегодный симпозиум по теоретическим аспектам компьютерной науки, Кашан, Франция, 13–15 февраля 1992 г., Труды , Lecture Notes in Computer Science, т. 577, Берлин: Springer, стр. 389–400, doi :10.1007/3-540-55210-3_199.
• Вессель, В.; Пёшель, Р. (1985), «О круговых графах», в Sachs, Horst (ред.), Графы, гиперграфы и приложения: Труды конференции по теории графов, состоявшейся в Эйбе с 1 по 5 октября 1984 г. , Teubner-Texte zur Mathematik, т. 73, BG Teubner, стр. 207–210. Как цитирует Унгер (1988).