Круг неразберихи

Размытая область в оптике

Диаграмма, показывающая круги нерезкости для точечного источника, расположенного слишком близко, в фокусе и слишком далеко

В оптике кружок нерезкости (КН) — это оптическое пятно, вызванное тем, что конус световых лучей от линзы не достигает идеального фокуса при отображении точечного источника . Он также известен как диск нерезкости , кружок нечеткости , размытый кружок или размытое пятно .

В фотографии кружок нерезкости используется для определения глубины резкости — части изображения, которая является приемлемо резкой. Стандартное значение CoC часто связано с каждым форматом изображения , но наиболее подходящее значение зависит от остроты зрения , условий просмотра и степени увеличения. Употребления в контексте включают максимально допустимый кружок нерезкости , предел диаметра кружка нерезкости и критерий кружка нерезкости .

Реальные линзы не фокусируют все лучи идеально, так что даже при лучшем фокусе точка отображается как пятно, а не как точка. Наименьшее такое пятно, которое может создать линза, часто называют кружком наименьшей нерезкости .

Два варианта использования

Необходимо различать два важных использования этого термина и концепции:

1. 

   В идеальной линзе L все лучи проходят через фокусную точку F. Однако на других расстояниях от линзы лучи образуют окружность.

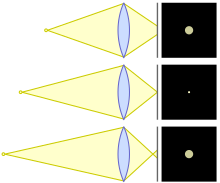
   Для описания самого большого пятна размытия, которое неотличимо от точки. Объектив может точно фокусировать объекты только на одном расстоянии; объекты на других расстояниях расфокусированы . Расфокусированные точки объекта изображаются как пятна размытия , а не как точки; чем больше расстояние объекта от плоскости фокусировки, тем больше размер пятна размытия. Такое пятно размытия имеет ту же форму, что и апертура объектива, но для простоты обычно рассматривается как круглое. На практике объекты на значительно разных расстояниях от камеры все еще могут казаться резкими; ^[1] диапазон расстояний до объекта, на котором объекты кажутся резкими, называется глубиной резкости (ГРИП). Общим критерием «приемлемой резкости» на конечном изображении (например, отпечатке, проекционном экране или электронном дисплее) является то, что пятно размытия должно быть неотличимо от точки.

2. 

   В несовершенной линзе L не все лучи проходят через фокус. Наименьший круг, через который они проходят , называется кругом наименьшей нерезкости.

   Для описания пятна размытия, достигаемого линзой, при ее лучшем фокусе или в более общем смысле. Признавая, что реальные линзы не фокусируют все лучи идеально даже при самых лучших условиях, термин « круг наименьшей нерезкости» часто используется для наименьшего пятна размытия, которое может создать линза, ^[2] например, путем выбора наилучшего положения фокуса, которое обеспечивает хороший компромисс между различными эффективными фокусными расстояниями различных зон линзы из-за сферических или других аберраций . Термин «круг нерезкости» применяется в более общем смысле, к размеру пятна вне фокуса, в которое линза отображает точку объекта. Дифракционные эффекты от волновой оптики и конечная апертура линзы определяют круг наименьшей нерезкости; ^[3] более общее использование «круга нерезкости» для точек вне фокуса может быть вычислено исключительно в терминах лучевой (геометрической) оптики. ^[4]

В идеализированной лучевой оптике, где предполагается, что лучи сходятся в точку при идеальной фокусировке, форма пятна размытия расфокусировки от линзы с круглой апертурой представляет собой круг света с жесткими краями. Более общее пятно размытия имеет мягкие края из-за дифракции и аберраций, ^{[5] [6]} и может быть некруглым из-за формы апертуры. Поэтому концепция диаметра должна быть тщательно определена, чтобы быть осмысленной. Подходящие определения часто используют концепцию замкнутой энергии , доли полной оптической энергии пятна, которая находится в пределах указанного диаметра. Значения доли (например, 80%, 90%) меняются в зависимости от приложения.

Предел диаметра кружка нерезкости в фотографии

В фотографии предел диаметра кружка нерезкости ( предел CoC или критерий CoC ) часто определяется как наибольшее пятно нерезкости, которое все еще будет восприниматься человеческим глазом как точка при просмотре на конечном изображении со стандартного расстояния просмотра. Предел CoC может быть указан на конечном изображении (например, отпечатке) или на исходном изображении (на пленке или датчике изображения).

При таком определении предел CoC в исходном изображении (изображении на пленке или электронном датчике) может быть установлен на основе нескольких факторов:

1. Острота зрения. Для большинства людей ближайшее комфортное расстояние просмотра, называемое близким расстоянием для отчетливого зрения , ^[7] составляет приблизительно 25 см. На этом расстоянии человек с хорошим зрением обычно может различить разрешение изображения в 5 пар линий на миллиметр (пл/мм), что эквивалентно CoC 0,2 мм на конечном изображении.
2. Условия просмотра. Если конечное изображение просматривается с расстояния примерно 25 см, CoC конечного изображения 0,2 мм часто является подходящим. Комфортное расстояние просмотра также такое, при котором угол обзора составляет примерно 60°; ^[7] на расстоянии 25 см это соответствует примерно 30 см, примерно диагонали изображения размером 8 × 10 дюймов (для сравнения, бумага формата A4 имеет размеры 8,3 × 11,7 дюйма, 210 мм × 297 мм; бумага формата US Letter имеет размеры 8,5 × 11 дюймов, 216 мм × 279 мм). Часто может быть разумным предположить, что для просмотра всего изображения конечное изображение размером более 8 × 10 дюймов будет просматриваться с расстояния, соответственно, большего, чем 25 см, и для которого больший CoC может быть приемлемым; CoC исходного изображения тогда такой же, как и определенный из стандартного размера конечного изображения и расстояния просмотра. Но если большее конечное изображение будет просматриваться с нормального расстояния 25 см, потребуется меньший CoC исходного изображения, чтобы обеспечить приемлемую резкость.
3. Увеличение от исходного изображения до конечного изображения. Если нет увеличения (например, контактная печать исходного изображения 8×10), CoC для исходного изображения такой же, как и в конечном изображении. Но если, например, длинный размер исходного изображения размером 35 мм увеличивается до 25 см (10 дюймов), коэффициент увеличения составляет приблизительно 7, а CoC для исходного изображения составляет 0,2 мм / 7, или 0,029 мм.

Общие значения для предела CoC могут быть неприменимы, если условия воспроизведения или просмотра существенно отличаются от тех, которые предполагались при определении этих значений. Если исходное изображение будет увеличено больше или просмотрено с более близкого расстояния, то потребуется меньший CoC. Все три фактора выше учитываются с помощью этой формулы:

CoC (в мм) = (расстояние просмотра (в см) / 25 см) / (желаемое разрешение конечного изображения в линиях/мм для расстояния просмотра 25 см) / увеличение

Например, для поддержки разрешения конечного изображения, эквивалентного 5 пар линий/мм для расстояния просмотра 25 см, когда предполагаемое расстояние просмотра составляет 50 см, а предполагаемое увеличение — 8:

CoC = (50 / 25) / 5 / 8 = 0,05 мм

Поскольку размер конечного изображения обычно неизвестен на момент съемки, принято предполагать стандартный размер, например, ширину 25 см, а также обычный CoC конечного изображения 0,2 мм, что составляет 1/1250 ширины изображения. Также широко используются соглашения в терминах диагональной меры. Глубину резкости, вычисленную с использованием этих соглашений, необходимо будет скорректировать, если исходное изображение обрезается перед увеличением до конечного размера изображения или если изменяются размеры и предположения о просмотре.

Для полнокадрового формата 35 мм (24 мм × 36 мм, диагональ 43 мм) широко используемый предел CoC составляет d /1500, или 0,029 мм для полнокадрового формата 35 мм, что соответствует разрешению 5 линий на миллиметр на отпечатке с диагональю 30 см. Значения 0,030 мм и 0,033 мм также распространены для полнокадрового формата 35 мм.

Также использовались критерии, связывающие CoC с фокусным расстоянием объектива. Kodak рекомендовал 2 минуты дуги ( критерий Снеллена 30 циклов/градус для нормального зрения) для критического просмотра, что дает CoC около f /1720, где f — фокусное расстояние объектива. ^[8] Для объектива 50 мм на полнокадровом формате 35 мм соответствующий CoC составляет 0,0291 мм. Этот критерий, очевидно, предполагал, что конечное изображение будет просматриваться на перспективно-правильном расстоянии (т. е. угол зрения будет таким же, как у исходного изображения):

Расстояние просмотра = фокусное расстояние снимающего объектива × увеличение

Однако изображения редко просматриваются на так называемом «правильном» расстоянии; зритель обычно не знает фокусного расстояния снимающего объектива, а «правильное» расстояние может быть неудобно коротким или длинным. Следовательно, критерии, основанные на фокусном расстоянии объектива, в целом уступили место критериям (таким как d /1500), связанным с форматом камеры.

Если изображение просматривается на носителе с низким разрешением, таком как монитор компьютера, то возможность обнаружения размытия будет ограничена средством отображения, а не человеческим зрением. Например, оптическое размытие будет сложнее обнаружить на изображении размером 8 × 10 дюймов, отображаемом на мониторе компьютера, чем на отпечатке 8 × 10 того же исходного изображения, просматриваемого с того же расстояния. Если изображение будет просматриваться только на устройстве с низким разрешением, может быть целесообразным больший CoC; однако, если изображение можно просматривать также на носителе с высоким разрешением, таком как отпечаток, будут определяющими критерии, обсуждаемые выше.

Формулы глубины резкости, полученные из геометрической оптики, подразумевают, что любая произвольная глубина резкости может быть достигнута с использованием достаточно малого CoC. Однако из-за дифракции это не совсем так. Использование меньшего CoC требует увеличения числа f объектива для достижения той же глубины резкости, и если объектив закрыт достаточно сильно, уменьшение размытия расфокусировки компенсируется увеличением размытия из-за дифракции. Более подробное обсуждение см. в статье Глубина резкости .

Предел диаметра кружка нерезкости основан наг/1500

Регулировка диаметра кружка нерезкости для шкалы глубины резкости объектива

Число f, определенное по шкале глубины резкости объектива, можно настроить так, чтобы оно отражало CoC, отличный от того, на котором основана шкала глубины резкости. В статье о глубине резкости показано , что

$${\displaystyle \mathrm {DoF} ={\frac {2Nc\left(m+1\right)}{m^{2}-\left({\frac {Nc}{f}}\right)^{2}}}\,,}$$

где N — диафрагменное число объектива, c — CoC, m — увеличение, а f — фокусное расстояние объектива. Поскольку диафрагменное число и CoC встречаются только как произведение Nc , увеличение одного из них эквивалентно соответствующему уменьшению другого. Например, если известно, что шкала глубины резкости объектива основана на CoC 0,035 мм, а фактические условия требуют CoC 0,025 мм, CoC необходимо уменьшить в 0,035/0,025 = 1,4 раза ; этого можно добиться, увеличив диафрагменное число, определенное по шкале DoF, в тот же самый раз или примерно на 1 стоп, поэтому объектив можно просто закрыть на 1 стоп от значения, указанного на шкале.

Тот же подход обычно можно использовать с калькулятором глубины резкости на камере обзора.

Определение диаметра кружка нерезкости по полю объекта

Диаграмма линз и лучей для расчета диаметра кружка нерезкости c для объекта, находящегося вне фокуса на расстоянии S ₂ , когда камера сфокусирована на S _1. Вспомогательный кружок нерезкости C в плоскости объекта (пунктирная линия) упрощает расчет.

Ранний расчет диаметра CoC («нечеткость»), выполненный «TH» в 1866 году.

Чтобы вычислить диаметр кружка нерезкости в плоскости изображения для объекта, находящегося вне фокуса, один из методов заключается в том, чтобы сначала вычислить диаметр кружка нерезкости в виртуальном изображении в плоскости объекта, что просто делается с помощью подобных треугольников, а затем умножить на увеличение системы, которое вычисляется с помощью уравнения линзы.

Круг размытия диаметром C в сфокусированной плоскости объекта на расстоянии S ₁ представляет собой несфокусированное мнимое изображение объекта на расстоянии S _{2 ,} как показано на диаграмме. Он зависит только от этих расстояний и диаметра апертуры A , через подобные треугольники, не зависящие от фокусного расстояния объектива:

$${\displaystyle C=A{|S_{2}-S_{1}| \over S_{2}}\,.}$$

Кружок нерезкости в плоскости изображения получается путем умножения на кратность m :

$${\displaystyle c=Cm\,,}$$

где увеличение m определяется отношением фокусных расстояний:

$${\displaystyle m={f_{1} \over S_{1}}\,.}$$

Используя уравнение линзы, мы можем решить для вспомогательной переменной f ₁ :

$${\displaystyle {1 \over f}={1 \over f_{1}}+{1 \over S_{1}}\,,}$$

что дает

$${\displaystyle f_{1}={fS_{1} \over S_{1}-f}\,,}$$

и выразим увеличение через фокусное расстояние и фокусное расстояние:

$${\displaystyle m={f \over S_{1}-f}\,,}$$

что дает конечный результат:

$${\displaystyle c=A{|S_{2}-S_{1}| \over S_{2}}{f \over S_{1}-f}\,.}$$

Это можно опционально выразить через диафрагменное число N = f/A следующим образом:

$${\displaystyle c={|S_{2}-S_{1}| \over S_{2}}{f^{2} \over N(S_{1}-f)}\,.}$$

Эта формула точна для простой параксиальной тонкой линзы или симметричной линзы, в которой входной и выходной зрачки имеют диаметр A. Более сложные конструкции линз с неединичным увеличением зрачка потребуют более сложного анализа, как это рассмотрено в разделе « Глубина резкости» .

В более общем смысле этот подход приводит к точному параксиальному результату для всех оптических систем, если A — диаметр входного зрачка , расстояния до объекта измеряются от входного зрачка, а увеличение известно:

$${\displaystyle c=Am{|S_{2}-S_{1}| \over S_{2}}\,.}$$

Если либо фокусное расстояние, либо расстояние до объекта вне фокуса бесконечно, уравнения можно оценить в пределе. Для бесконечного фокусного расстояния:

$${\displaystyle c={fA \over S_{2}}={f^{2} \over NS_{2}}\,.}$$

А для размытого круга объекта на бесконечности, когда фокусное расстояние конечно:

$${\displaystyle c={fA \over S_{1}-f}={f^{2} \over N(S_{1}-f)}\,.}$$

Если значение c зафиксировано как предел диаметра кружка нерезкости, то любое из этих уравнений можно решить относительно расстояния до объекта, чтобы получить гиперфокальное расстояние , с приблизительно эквивалентными результатами.

История

Генри Коддингтон 1829

До того, как это было применено к фотографии, концепция кружка нерезкости применялась к оптическим приборам, таким как телескопы. Коддингтон (1829, стр. 54) количественно определяет как кружок наименьшей нерезкости , так и наименьший кружок нерезкости для сферической отражающей поверхности.

Это мы можем считать ближайшим приближением к простому фокусу и называть кругом наименьшей неясности .

Общество по распространению полезных знаний 1832 г.

Общество по распространению полезных знаний (1832, стр. 11) применило его к аберрациям третьего порядка:

Эта сферическая аберрация производит нечеткость видения, разбрасывая каждую математическую точку объекта в маленькое пятно на его изображении; эти пятна, смешиваясь друг с другом, запутывают целое. Диаметр этого круга нерезкости в фокусе центральных лучей F, по которому распределена каждая точка, будет LK (рис. 17.); и когда апертура рефлектора умеренная, он равен кубу апертуры, деленному на квадрат радиуса (...): этот круг называется аберрацией широты.

ТН 1866

Расчеты кружка нерезкости: Ранним предшественником расчетов глубины резкости является расчет TH (1866, стр. 138) диаметра кружка нерезкости от расстояния до объекта для объектива, сфокусированного на бесконечности; на эту статью указал фон Рор (1899). Формула, которую он придумал для того, что он называет «нечеткостью», эквивалентна, в современных терминах,

$${\displaystyle c={fA \over S}}$$

для фокусного расстояния f , диаметра диафрагмы A и расстояния до объекта S. Но он не инвертирует это, чтобы найти S , соответствующее данному критерию c (т. е. он не решает для гиперфокального расстояния ), и не рассматривает фокусировку на каком-либо другом расстоянии, кроме бесконечности.

Наконец, он замечает, что «длиннофокусные объективы обычно имеют большую апертуру, чем короткофокусные, и по этой причине имеют меньшую глубину фокуса» [курсив его].

Даллмейер и Эбни

Даллмейер (1892, стр. 24) в расширенном переиздании брошюры своего отца Джона Генри Даллмейера 1874 года (Dallmeyer 1874) « О выборе и использовании фотографических объективов» (в материале, которого нет в издании 1874 года и который, по-видимому, был добавлен из статьи Дж. Х. Даллмейера «Об использовании диафрагм или стопоров», дата которой неизвестна), говорит:

Таким образом, каждая точка объекта, находящаяся вне фокуса, представлена ​​на снимке диском или кружком нерезкости, размер которого пропорционален апертуре по отношению к фокусу используемого объектива. Если точка объекта находится вне фокуса на 1/100 дюйма, она будет представлена ​​кружком нерезкости, размером всего лишь в 1/100 часть апертуры объектива.

Последнее утверждение явно неверно или искажено, поскольку оно не соответствует действительности на величину фокусного расстояния (фокусного расстояния). Он продолжает:

и когда круги неясности достаточно малы, глаз не видит их как таковые; тогда они видны только как точки, и изображение кажется резким. На обычном расстоянии зрения, от двенадцати до пятнадцати дюймов, круги неясности видны как точки, если угол, образуемый ими, не превышает одной угловой минуты или, грубо говоря, если они не превышают 1/100 дюйма в диаметре.

В числовом выражении 1/100 дюйма на расстоянии 12–15 дюймов ближе к двум минутам дуги. Этот выбор предела CoC остается (для крупного шрифта) наиболее широко используемым даже сегодня. Эбни (1881, стр. 207–208) использует аналогичный подход, основанный на остроте зрения в одну минуту дуги, и выбирает кружок нерезкости 0,025 см для просмотра на расстоянии 40–50 см, по сути, делая ту же ошибку в два раза в метрических единицах. Неясно, кто из них, Эбни или Даллмейер, установил стандарт CoC раньше.

Стена 1889 г.

Обычный предел CoC в 1/100 дюйма применялся к размытию, отличному от размытия расфокусировки. Например, Уолл (1889, стр. 92) говорит:

Чтобы узнать, насколько быстро должен срабатывать затвор, чтобы запечатлеть движущийся объект так, чтобы образовался кружок нерезкости диаметром менее 1/100 дюйма, разделите расстояние до объекта на 100 фокусных расстояний объектива и разделите скорость движения объекта в дюймах в секунду на результат, получив при этом наибольшую продолжительность экспозиции в долях секунды.

Смотрите также

• Диск Эйри
• Астигматизм
• Боке
• Хроматическая аберрация
• Фокальное облако
• Орб (оптика)
• Функция рассеяния точки
• формула Цейсса

Примечания

1. Рэй 2000, стр. 50.
2. Рэй 2002, стр. 89.
3. J.-A. Beraldin; et al. (2006). "Виртуальная реконструкция объектов культурного наследия: возможности и проблемы, созданные 3D-технологиями". В Manos Baltsavias; Armin Gruen; Luc Van Gool; Maria Pateraki (ред.). Recording, modeling and visualization of Cultural Heritage . Taylor & Francis. p. 145. ISBN 978-0-415-39208-2.
4. Уолтер Балкли Ковентри (1901). Техника ручной камеры. Sands & Co. стр. 9.
5. Стоксет 1969, стр. 1317.
6. Мерклингер 1992, стр. 45–46.
7. Ray 2000, стр. 52.
8. Кодак 1972, стр. 5.
9. Размер кадра — это среднее значение камер, которые делают фотографии этого формата. Например, не все камеры 6×7 делают кадры, которые точно56 мм  ×69 мм . Проверьте характеристики конкретной камеры, требуется ли такой уровень точности.
10. " APS-C " — это распространенный формат для цифровых зеркальных фотокамер. Размеры немного различаются у разных производителей; например, формат APS-C от Canon номинально15,0 мм  ×22,5 мм , тогда как формат DX от Nikon номинально16 мм  ×24 мм . Точные размеры иногда немного различаются среди моделей с одинаковым номинальным форматом у данного производителя.

Ссылки

• Эбни, сэр Уильям де Вивелсли (1881). Трактат о фотографии. Лондон: Longmans, Green and Co.
• Коддингтон, Генри (1829). Трактат об отражении и преломлении света: часть I системы оптики. Кембридж: Дж. Смит.
• Даллмейер, Джон Генри (1874). О выборе и использовании фотографических объективов . Нью-Йорк: E. and HT Anthony and Co.
• Даллмейер, Томас Р. (1892). О выборе и использовании фотографических объективов . Лондон: J. Pitcher.
• Eastman Kodak Company (1972). Оптические формулы и их применение, Kodak Publication No. AA-26, Rev. 11-72-BX . Рочестер, Нью-Йорк: Eastman Kodak Company.
• Мерклингер, Гарольд М. (1992). Плюсы и минусы ФОКУСА: альтернативный способ оценки глубины резкости и резкости фотографического изображения (PDF) . Бедфорд, Новая Шотландия: HM Merklinger. ISBN 0-9695025-0-8.
• Рэй, Сидней Ф. (2000). «Геометрия формирования изображения». В Ральф Э. Якобсон; Сидней Ф. Рэй; Джеффри Г. Аттеридж; Норман Р. Аксфорд (ред.). Руководство по фотографии: фотографические и цифровые изображения (9-е изд.). Оксфорд: Focal Press. ISBN 0-240-51574-9.
• Рэй, Сидни Ф. (2002). Прикладная фотографическая оптика (3-е изд.). Оксфорд: Focal. ISBN 0-240-51540-4.
• Общество распространения полезных знаний (1832). Натуральная философия: с объяснением научных терминов и индексом . Лондон: Baldwin and Cradock, Paternoster-Row.
• Stokseth, Per A. (октябрь 1969). «Свойства расфокусированной оптической системы». Журнал оптического общества Америки . 59 (10): 1314. Bibcode : 1969JOSA...59.1314S. doi : 10.1364/JOSA.59.001314.
• TH [псевд.] (1866). «Длинный и короткий фокус». British Journal of Photography (13).
• фон Рор, Мориц (1899). Фотография Объектив . Берлин: Verlag Юлиус Шпрингер.
• Уолл, Эдвард Джон (1889). Словарь фотографии для любителей и профессиональных фотографов . Нью-Йорк: E. and HT Anthony and Co.

Внешние ссылки

• Круги нерезкости для цифровых камер – DOFMaster
• Глубина резкости в глубине (PDF) – включает обсуждение критериев кружка нерезкости
• Что такое «круг неясности» – руководство ƒ/Calc