Кубическая функция

Полиномиальная функция степени 3

График кубической функции с 3 действительными корнями (где кривая пересекает горизонтальную ось — где y = 0 ). Показанный случай имеет две критические точки . Здесь функция имеет вид f ( x ) = ( x ³ + 3 x ² − 6 x − 8)/4 .

В математике кубическая функция — это функция вида , то есть полиномиальная функция третьей степени. Во многих текстах коэффициенты a , b , c и d считаются действительными числами , а функция рассматривается как действительная функция , которая отображает действительные числа в действительные числа, или как комплексная функция, которая отображает комплексные числа в комплексные числа. В других случаях коэффициенты могут быть комплексными числами, а функция — это комплексная функция, которая имеет множество комплексных чисел в качестве своего домена , даже если домен ограничен действительными числами. ${\displaystyle f(x)=ax^{3}+bx^{2}+cx+d,}$

При задании f ( x ) = 0 получается кубическое уравнение вида

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

решения которого называются корнями функции. Производная кубической функции является квадратичной функцией .

Кубическая функция с действительными коэффициентами имеет один или три действительных корня ( которые могут не быть различны ); ^[1] все многочлены нечетной степени с действительными коэффициентами имеют по крайней мере один действительный корень.

График кубической функции всегда имеет одну точку перегиба . Он может иметь две критические точки , локальный минимум и локальный максимум. В противном случае кубическая функция монотонна . График кубической функции симметричен относительно своей точки перегиба; то есть он инвариантен относительно поворота на пол-оборота вокруг этой точки. С точностью до аффинного преобразования существует только три возможных графика для кубических функций.

Кубические функции являются основополагающими для кубической интерполяции .

История

Критические и переломные точки

Корни , стационарные точки , точка перегиба и вогнутость кубического многочлена x 3 ⁻ 6 x ² + 9 x − 4 (сплошная черная кривая) и его первая (пунктирная красная) и вторая (пунктирная оранжевая ) производные .

Критические точки кубической функции — это ее стационарные точки , то есть точки, в которых наклон функции равен нулю. ^[2] Таким образом, критические точки кубической функции f определяются как

f ( x ) = ax ³ + bx ² + cx + d ,

происходят при таких значениях x , что производная

${\displaystyle 3ax^{2}+2bx+c=0}$

кубической функции равен нулю.

Решения этого уравнения являются значениями x критических точек и определяются с помощью квадратной формулы следующим образом:

${\displaystyle x_{\text{critical}}={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.}$

Знак выражения Δ ₀ = b ² – 3 ac внутри квадратного корня определяет количество критических точек. Если он положительный, то имеется две критические точки, одна из которых является локальным максимумом, а другая – локальным минимумом. Если b ² – 3 ac = 0 , то имеется только одна критическая точка, которая является точкой перегиба . Если b ² – 3 ac < 0 , то (действительных) критических точек нет. В двух последних случаях, то есть если b ² – 3 ac неположительно, кубическая функция строго монотонна . Пример случая Δ ₀ > 0 см . на рисунке.

Точка перегиба функции находится там, где эта функция меняет вогнутость . ^[3] Точка перегиба возникает, когда вторая производная равна нулю, а третья производная не равна нулю. Таким образом, кубическая функция всегда имеет одну точку перегиба, которая возникает при ${\displaystyle f''(x)=6ax+2b,}$

${\displaystyle x_{\text{inflection}}=-{\frac {b}{3a}}.}$

Классификация

Кубические функции вида График любой кубической функции подобен такой кривой. ${\displaystyle y=x^{3}+cx.}$

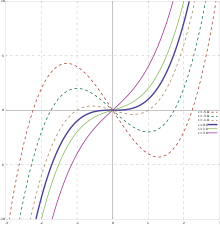
График кубической функции представляет собой кубическую кривую , хотя многие кубические кривые не являются графиками функций.

Хотя кубические функции зависят от четырех параметров, их график может иметь лишь очень немного форм. Фактически, график кубической функции всегда похож на график функции вида

${\displaystyle y=x^{3}+px.}$

Это подобие может быть построено как композиция переносов , параллельных осям координат, гомотеции ( равномерного масштабирования ) и, возможно, отражения ( зеркального отображения ) относительно оси Y. Дальнейшее неравномерное масштабирование может преобразовать график в график одной из трех кубических функций

${\displaystyle {\begin{aligned}y&=x^{3}+x\\y&=x^{3}\\y&=x^{3}-x.\end{aligned}}}$

Это означает, что с точностью до аффинного преобразования существует только три графика кубических функций .

Вышеуказанные геометрические преобразования можно построить следующим образом, исходя из общей кубической функции ${\displaystyle y=ax^{3}+bx^{2}+cx+d.}$

Во-первых, если a < 0 , то замена переменной x → – x позволяет предположить a > 0. После этой замены переменной новый график является зеркальным отражением предыдущего относительно оси y .

Тогда замена переменной x = x ₁ – ⁠б/3 а⁠ обеспечивает функцию вида

${\displaystyle y=ax_{1}^{3}+px_{1}+q.}$

Это соответствует перемещению параллельно оси x .

Замена переменной y = y ₁ + q соответствует переносу относительно оси y и дает функцию вида

${\displaystyle y_{1}=ax_{1}^{3}+px_{1}.}$

Изменение переменной соответствует равномерному масштабированию и дает после умножения на функцию вида ${\displaystyle \textstyle x_{1}={\frac {x_{2}}{\sqrt {a}}},y_{1}={\frac {y_{2}}{\sqrt {a}}}}$ ${\displaystyle {\sqrt {a}},}$

${\displaystyle y_{2}=x_{2}^{3}+px_{2},}$

что является простейшей формой, которую можно получить путем подобия.

Тогда, если p ≠ 0 , неравномерное масштабирование дает после деления на ${\displaystyle \textstyle x_{2}=x_{3}{\sqrt {|p|}},\quad y_{2}=y_{3}{\sqrt {|p|^{3}}}}$ ${\displaystyle \textstyle {\sqrt {|p|^{3}}},}$

${\displaystyle y_{3}=x_{3}^{3}+x_{3}\operatorname {sgn}(p),}$

где имеет значение 1 или –1, в зависимости от знака p . Если определить последнюю форму функции, то она применима ко всем случаям (с и ). ${\displaystyle \operatorname {sgn}(p)}$ ${\displaystyle \operatorname {sgn}(0)=0,}$ ${\displaystyle x_{2}=x_{3}}$ ${\displaystyle y_{2}=y_{3}}$

Симметрия

Для кубической функции вида точка перегиба является началом координат. Поскольку такая функция является нечетной функцией , ее график симметричен относительно точки перегиба и инвариантен относительно поворота на пол-оборота вокруг точки перегиба. Поскольку эти свойства инвариантны по подобию , следующее справедливо для всех кубических функций. ${\displaystyle y=x^{3}+px,}$

График кубической функции симметричен относительно точки перегиба и инвариантен при повороте на пол-оборота вокруг точки перегиба.

Коллинеарности

Точки P ₁ , P ₂ и P ₃ (синего цвета) лежат на одной прямой и принадлежат графику функции x ³ + ⁠3/2⁠ х ² − ⁠5/2⁠ х + ⁠5/4⁠ . Точки T ₁ , T ₂ и T ₃ (красные) являются пересечениями (пунктирных) касательных к графику в этих точках с самим графиком. Они также коллинеарны.

Касательные линии к графику кубической функции в трех коллинеарных точках снова пересекают кубическую функцию в коллинеарных точках. ^[4] Это можно увидеть следующим образом.

Поскольку это свойство инвариантно относительно жесткого движения , можно предположить, что функция имеет вид

${\displaystyle f(x)=x^{3}+px.}$

Если α — действительное число, то касательная к графику функции f в точке ( α , f ( α )) — это прямая

{( Икс , ж ( α ) + ( Икс - α ) ж  ′( α )) : Икс ∈ р } .

Итак, точку пересечения этой линии с графиком функции f можно получить, решив уравнение f ( x ) = f ( α ) + ( x − α ) f  ′( α ) , то есть

${\displaystyle x^{3}+px=\alpha ^{3}+p\alpha +(x-\alpha )(3\alpha ^{2}+p),}$

который можно переписать

${\displaystyle x^{3}-3\alpha ^{2}x+2\alpha ^{3}=0,}$

и факторизуется как

${\displaystyle (x-\alpha )^{2}(x+2\alpha )=0.}$

Итак, касательная пересекает кубическую прямую в точке

${\displaystyle (-2\alpha ,-8\alpha ^{3}-2p\alpha )=(-2\alpha ,-8f(\alpha )+6p\alpha ).}$

Итак, функция, которая отображает точку ( x , y ) графика в другую точку, где касательная пересекает график, имеет вид

${\displaystyle (x,y)\mapsto (-2x,-8y+6px).}$

Это аффинное преобразование , которое преобразует коллинеарные точки в коллинеарные точки. Это доказывает заявленный результат.

Кубическая интерполяция

Если заданы значения функции и ее производной в двух точках, то существует ровно одна кубическая функция, которая имеет те же четыре значения, и она называется кубическим сплайном Эрмита .

Существует два стандартных способа использования этого факта. Во-первых, если известны, например, путем физического измерения, значения функции и ее производной в некоторых точках выборки, можно интерполировать функцию с помощью непрерывно дифференцируемой функции , которая является кусочно- кубической функцией.

Если значение функции известно в нескольких точках, кубическая интерполяция заключается в аппроксимации функции непрерывно дифференцируемой функцией , которая является кусочно- кубической. Для получения однозначно определенной интерполяции необходимо добавить еще два ограничения, такие как значения производных в конечных точках или нулевая кривизна в конечных точках.

Ссылки

1. Босток, Линда; Чандлер, Сюзанна; Чандлер, Ф.С. (1979). Чистая математика 2. Нельсон Торнс. стр. 462. ISBN 978-0-85950-097-5. Таким образом, кубическое уравнение имеет либо три действительных корня... либо один действительный корень...
2. Weisstein, Eric W. "Stationary Point". mathworld.wolfram.com . Получено 27.07.2020 .
3. Хьюз-Халлетт, Дебора; Лок, Патти Фрейзер; Глисон, Эндрю М.; Флат, Дэниел Э.; Гордон, Шелдон П.; Ломен, Дэвид О.; Лавлок, Дэвид; МакКаллум, Уильям Г.; Осгуд, Брэд Г. (11 декабря 2017 г.). Прикладное исчисление. John Wiley & Sons. стр. 181. ISBN 978-1-119-27556-5Точка, в которой график функции f меняет вогнутость, называется точкой перегиба функции f .
4. Уитворт, Уильям Аллен (1866), «Уравнения третьей степени», Трилинейные координаты и другие методы современной аналитической геометрии двух измерений, Кембридж: Deighton, Bell, and Co., стр. 425 , получено 17 июня 2016 г.

Внешние ссылки

• «Формула Кардано», Энциклопедия математики , EMS Press , 2001 [1994]
• История квадратных, кубических и четвертых уравнений в архиве MacTutor .