Преобразование данных (статистика)

Диаграмма рассеяния , на которой площади суверенных государств и зависимых территорий мира отложены на вертикальной оси против их населения на горизонтальной оси. Верхний график использует необработанные данные. На нижнем графике данные о площади и населении были преобразованы с использованием функции логарифма.

В статистике преобразование данных — это применение детерминированной математической функции к каждой точке набора данных , то есть каждая точка данных z _i заменяется преобразованным значением y _i = f ( zi ₎ , где f — функция. Преобразования обычно применяются для того, чтобы данные выглядели более точно соответствующими предположениям применяемой процедуры статистического вывода , или для улучшения интерпретируемости или внешнего вида графиков .

Почти всегда функция, используемая для преобразования данных, является обратимой и, как правило, непрерывной . Преобразование обычно применяется к набору сопоставимых измерений. Например, если мы работаем с данными о доходах людей в какой-либо денежной единице, обычно значение дохода каждого человека преобразуется с помощью функции логарифма .

Мотивация

Рекомендации относительно того, как следует преобразовывать данные или следует ли вообще применять преобразование, должны основываться на конкретном статистическом анализе, который необходимо выполнить. Например, простой способ построить приблизительный 95% доверительный интервал для среднего значения генеральной совокупности — это взять выборочное среднее плюс-минус две единицы стандартной ошибки . Однако используемый здесь постоянный коэффициент 2 характерен для нормального распределения и применим только в том случае, если выборочное среднее изменяется примерно нормально. Центральная предельная теорема утверждает, что во многих ситуациях выборочное среднее изменяется нормально, если размер выборки достаточно велик. Однако если совокупность существенно искажена , а размер выборки не более чем умеренный, приближение, обеспечиваемое центральной предельной теоремой, может быть плохим, и полученный доверительный интервал, скорее всего, будет иметь неправильную вероятность охвата . Таким образом, когда есть свидетельства существенного искажения данных, перед построением доверительного интервала обычно преобразуют данные к симметричному распределению ^[1] . При желании доверительный интервал затем можно преобразовать обратно в исходную шкалу, используя обратное преобразованию, которое было применено к данным. ^{[2] [3]}

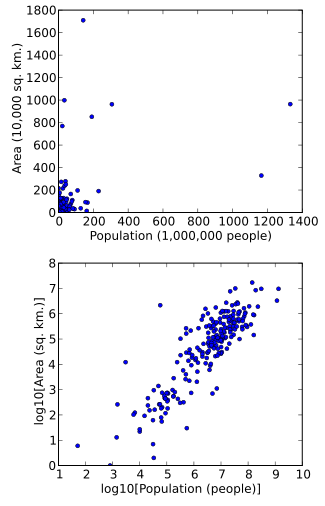
Данные также можно преобразовать, чтобы их было легче визуализировать. Например, предположим, что у нас есть диаграмма рассеяния, на которой точками являются страны мира, а отображаемые значения данных — это площадь суши и население каждой страны. Если график построен с использованием непреобразованных данных (например, квадратные километры площади и количество людей для населения), большинство стран будут отображены в виде плотного кластера точек в левом нижнем углу графика. Несколько стран с очень большой территорией и/или населением будут разбросаны по большей части площади графика. Простое изменение масштаба единиц измерения (например, до тысяч квадратных километров или миллионов человек) не изменит ситуацию. Однако после логарифмических преобразований площади и численности населения точки будут распределены на графике более равномерно.

Другой причиной применения преобразования данных является улучшение интерпретируемости, даже если не требуется проводить формальный статистический анализ или визуализацию. Например, предположим, что мы сравниваем автомобили с точки зрения их экономии топлива. Эти данные обычно представляются как «километры на литр» или «мили на галлон». Однако, если цель состоит в том, чтобы оценить, сколько дополнительного топлива человек будет использовать за один год при вождении одного автомобиля по сравнению с другим, более естественно работать с данными, преобразованными путем применения обратной функции , что дает литры на километр или галлоны. за милю.

В регрессии

Преобразование данных можно использовать в качестве меры по исправлению ситуации, чтобы сделать данные пригодными для моделирования с помощью линейной регрессии , если исходные данные нарушают одно или несколько предположений линейной регрессии. ^[4] Например, простейшие модели линейной регрессии предполагают линейную связь между ожидаемым значением Y ( переменной ответа, которую нужно предсказать) и каждой независимой переменной (когда другие независимые переменные остаются фиксированными). Если линейность не сохраняется, даже приблизительно, иногда можно преобразовать независимые или зависимые переменные в регрессионной модели, чтобы улучшить линейность. ^[5] Например, добавление квадратичных функций исходных независимых переменных может привести к линейной зависимости с ожидаемым значением Y , что приводит к модели полиномиальной регрессии , частному случаю линейной регрессии.

Еще одним предположением линейной регрессии является гомоскедастичность , то есть дисперсия ошибок должна быть одинаковой независимо от значений предикторов. Если это предположение нарушается (т. е. если данные гетероскедастичны ), возможно найти преобразование только Y или преобразования как X ( переменные-предикторы ) и Y , так что предположение о гомоскедастичности (в дополнение к линейности предположение) справедливо для преобразованных переменных ^[5] , и поэтому к ним можно применять линейную регрессию.

Еще одним применением преобразования данных является решение проблемы отсутствия нормальности с точки зрения ошибок. Одномерная нормальность не требуется для того, чтобы оценки параметров регрессии методом наименьших квадратов были значимыми (см. теорему Гаусса – Маркова ). Однако доверительные интервалы и проверки гипотез будут иметь лучшие статистические свойства, если переменные демонстрируют многомерную нормальность . Преобразования, которые стабилизируют дисперсию ошибок (т.е. те, которые устраняют гетероскедичность), часто также помогают сделать ошибки примерно нормальными. ^{[5] [6]}

Примеры

Уравнение: ${\displaystyle Y=a+bX}$

Значение: Увеличение X на единицу связано со средним увеличением Y на b единиц.

Уравнение: ${\displaystyle \log(Y)=a+bX}$

(Из возведения в степень обеих частей уравнения: ) ${\displaystyle Y=e^{a}e^{bX}}$

Значение: Увеличение единицы X связано со средним увеличением b единиц в или, что то же самое, Y увеличивается в среднем на мультипликативный коэффициент . Для иллюстративных целей, если бы вместо натурального логарифма в приведенном выше преобразовании использовался логарифм по основанию 10 и те же символы ( a и b ) использовались для обозначения коэффициентов регрессии, то увеличение X на единицу привело бы к увеличению Y в раз. в среднем. Если бы b было равно 1, то это подразумевало бы 10-кратное увеличение Y при единичном увеличении X. ${\displaystyle \log(Y)}$ ${\displaystyle e^{b}\!}$ ${\displaystyle 10^{b}}$

Уравнение: ${\displaystyle Y=a+b\log(X)}$

Значение: увеличение X в k раз связано со средним увеличением единиц Y. Для иллюстративных целей, если в приведенном выше преобразовании вместо натурального логарифма использовался логарифм по основанию 10 и использовались те же символы ( a и b ). для обозначения коэффициентов регрессии, то десятикратное увеличение X приведет к среднему увеличению единиц Y. ${\displaystyle b\times \log(k)}$ ${\displaystyle b\times \log _{10}(10)=b}$

Уравнение: ${\displaystyle \log(Y)=a+b\log(X)}$

(Из возведения в степень обеих частей уравнения: ) ${\displaystyle Y=e^{a}X^{b}}$

Значение: увеличение X в k раз связано с мультипликативным увеличением Y в среднем. Таким образом, если X удвоится, это приведет к изменению Y на мультипликативный коэффициент . ^[7] ${\displaystyle k^{b}}$ ${\displaystyle 2^{b}\!}$

Альтернатива

Обобщенные линейные модели (GLM) обеспечивают гибкое обобщение обычной линейной регрессии, которое позволяет использовать переменные отклика, которые имеют модели распределения ошибок, отличные от нормального распределения. GLM позволяют связать линейную модель с переменной отклика через функцию связи и позволяют величине дисперсии каждого измерения быть функцией его прогнозируемого значения. ^{[8] [9]}

Распространенные случаи

Преобразование логарифма и преобразование квадратного корня обычно используются для положительных данных, а мультипликативное обратное преобразование ( обратное преобразование ) может использоваться для ненулевых данных. Степенное преобразование — это семейство преобразований, параметризованное неотрицательным значением λ, которое включает в себя логарифмирование, квадратный корень и мультипликативные обратные преобразования в качестве особых случаев. Чтобы систематически подходить к преобразованию данных, можно использовать методы статистической оценки для оценки параметра λ при степенном преобразовании, тем самым определяя преобразование, которое является примерно наиболее подходящим в данной ситуации. Поскольку семейство степенных преобразований также включает в себя преобразование идентичности, этот подход также может указать, будет ли лучше анализировать данные без преобразования. В регрессионном анализе этот подход известен как преобразование Бокса-Кокса .

Обратное преобразование, некоторые степенные преобразования, такие как преобразование Йео-Джонсона , и некоторые другие преобразования, такие как применение обратного гиперболического синуса , могут быть осмысленно применены к данным, которые включают как положительные, так и отрицательные значения ^[10] (степенное преобразование обратимо по все действительные числа, если λ — нечетное целое число). Однако, когда наблюдаются как отрицательные, так и положительные значения, иногда принято начинать с добавления константы ко всем значениям, создавая набор неотрицательных данных, к которым можно применить любое степенное преобразование. ^[3]

Обычной ситуацией, когда применяется преобразование данных, является ситуация, когда интересующее значение варьируется в пределах нескольких порядков величины . Многие физические и социальные явления демонстрируют такое поведение — доходы, популяции видов, размеры галактик и объёмы осадков, и это лишь некоторые из них. Степенные преобразования и, в частности, логарифмирование часто можно использовать для обеспечения симметрии таких данных. Логарифм часто отдается предпочтение, поскольку его результат легко интерпретировать с точки зрения «кратности изменений».

Логарифм также оказывает полезное влияние на отношения. Если мы сравниваем положительные величины X и Y , используя соотношение X  /  Y , то если X  <  Y , отношение находится в интервале (0,1), тогда как если X  >  Y , отношение находится в полупрямом (1 ,∞), где отношение 1 соответствует равенству. В анализе, где X и Y рассматриваются симметрично, логарифмическое отношение log( X  /  Y ) равно нулю в случае равенства и обладает тем свойством, что если X в K раз больше, чем Y , логарифмическое отношение является эквидистантно от нуля, как в ситуации, когда Y в K раз больше, чем X (логарифмические отношения равны log( K ) и −log( K ) в этих двух ситуациях).

Если значения естественным образом ограничены диапазоном от 0 до 1, не включая конечные точки, тогда может подойти логит-преобразование : это дает значения в диапазоне (-∞, ∞).

Превращение в нормальность

1. Не всегда необходимо или желательно преобразовывать набор данных так, чтобы он напоминал нормальное распределение. Однако, если желательны симметрия или нормальность, их часто можно вызвать с помощью одного из степенных преобразований.

2. Лингвистическая степенная функция распределяется по закону Ципфа-Мандельброта . Распределение чрезвычайно колючее и лептокуртическое , поэтому исследователям пришлось отказаться от статистики, чтобы решить, например, проблемы установления авторства . Тем не менее, использование гауссовой статистики вполне возможно путем применения преобразования данных. ^[11]

3. Для оценки того, была ли достигнута нормальность после преобразования, можно использовать любой из стандартных тестов на нормальность . Графический подход обычно более информативен, чем формальный статистический тест, и поэтому для оценки соответствия набора данных нормальной популяции обычно используется обычный квантильный график . В качестве альтернативы также были предложены эмпирические правила, основанные на асимметрии выборки и эксцессе . ^{[12] [13]}

Преобразование к равномерному распределению или произвольному распределению

Если мы наблюдаем набор из n значений X ₁ , ..., X _n без каких-либо связей (т. е. существует n различных значений), мы можем заменить X _i преобразованным значением Y _i = k , где k определено так, что X _i является k- ^м по величине среди всех значений X. Это называется ранговым преобразованием [ ^14] и создает данные, идеально подходящие для равномерного распределения . Этот подход имеет популяционный аналог.

Используя преобразование интеграла вероятности , если X — любая случайная величина , а F — кумулятивная функция распределения X , то, пока F обратима, случайная величина U = F ( X ) следует равномерному распределению на единичном интервале [0 ,1].

Из равномерного распределения мы можем перейти к любому распределению с обратимой кумулятивной функцией распределения. Если G — обратимая кумулятивная функция распределения, а U — равномерно распределенная случайная величина, то случайная величина G ⁻¹ ( U ) имеет G в качестве кумулятивной функции распределения.

Объединив эти два понятия, если X — любая случайная величина, F — обратимая кумулятивная функция распределения X , а G — обратимая кумулятивная функция распределения, то случайная величина G ⁻¹ ( F ( X )) имеет G в качестве своей кумулятивной функции распределения. .

Преобразования, стабилизирующие дисперсию

Многие типы статистических данных демонстрируют « отношение дисперсии к среднему», что означает, что изменчивость различна для значений данных с разными ожидаемыми значениями . Например, при сравнении различных групп населения в мире разница в доходах имеет тенденцию увеличиваться по мере увеличения среднего дохода. Если мы рассмотрим несколько небольших единиц территории (например, округа в Соединенных Штатах) и получим среднее значение и дисперсию доходов внутри каждого округа, то, как правило, округа с более высоким средним доходом также будут иметь более высокие отклонения.

Преобразование , стабилизирующее дисперсию, направлено на устранение зависимости дисперсии от среднего, чтобы дисперсия стала постоянной относительно среднего. Примерами преобразований, стабилизирующих дисперсию, являются преобразование Фишера для выборочного коэффициента корреляции, преобразование квадратного корня или преобразование Анскомба для данных Пуассона (данные подсчета), преобразование Бокса-Кокса для регрессионного анализа, а также арксинусное преобразование квадратного корня или угловое преобразование для пропорции ( биномиальные данные). Хотя арксинусное преобразование квадратного корня обычно используется для статистического анализа пропорциональных данных, оно не рекомендуется, поскольку логистическая регрессия или логит-преобразование более подходят для биномиальных или небиномиальных пропорций соответственно, особенно из-за уменьшения ошибки типа II . ^{[15] [3]}

Преобразования для многомерных данных

Одномерные функции можно точечно применять к многомерным данным, чтобы изменить их маргинальные распределения. Также возможно изменить некоторые атрибуты многомерного распределения, используя соответствующим образом построенное преобразование. Например, при работе с временными рядами и другими типами последовательных данных обычно данные различают для улучшения стационарности . Если данные, сгенерированные случайным вектором X, наблюдаются как векторы X _i наблюдений с ковариационной матрицей Σ, для декорреляции данных можно использовать линейное преобразование . Для этого используется разложение Холецкого , выражающее Σ = A A' . Тогда преобразованный вектор Y _i = A ⁻¹ X _i имеет единичную матрицу в качестве ковариационной матрицы.

Смотрите также

• Арксин
• Разработка функций
• Логит
• Нелинейная регрессия § Преобразование
• Коэффициент корреляции Пирсона
• Силовое преобразование (Бокс – Кокс)
• Преобразование Вильсона – Хилферти
• Отбеливание трансформации

Рекомендации

1. Кун, Макс; Джонсон, Кьелл (2013). Прикладное прогнозное моделирование . Нью-Йорк. дои : 10.1007/978-1-4614-6849-3. ISBN 9781461468493. LCCN  2013933452. OCLC  844349710. S2CID  60246745.{{cite book}}: CS1 maint: location missing publisher (link)
2. Альтман, Дуглас Г.; Бланд, Дж. Мартин (27 апреля 1996 г.). «Статистические примечания: преобразования, средние значения и доверительные интервалы». БМЖ . 312 (7038): 1079. doi :10.1136/bmj.312.7038.1079. ISSN  0959-8138. ПМК 2350916 . ПМИД  8616417. 
3. «Преобразование данных - Справочник по биологической статистике». www.biostathandbook.com . Проверено 19 марта 2019 г.
4. «Урок 9: Преобразования данных | STAT 501» . newonlinecourses.science.psu.edu . Проверено 17 марта 2019 г.
5. Катнер, Майкл Х.; Нахтсхайм, Кристофер Дж.; Нетер, Джон; Ли, Уильям (2005). Прикладные линейные статистические модели (5-е изд.). Бостон: МакГроу-Хилл Ирвин. стр. 129–133. ISBN 0072386886. LCCN  2004052447. OCLC  55502728.
6. Альтман, Дуглас Г.; Бланд, Дж. Мартин (23 марта 1996 г.). «Статистические примечания: преобразование данных». БМЖ . 312 (7033): 770. doi :10.1136/bmj.312.7033.770. ISSN  0959-8138. ПМК 2350481 . ПМИД  8605469. 
7. «9.3 - Логарифмическое преобразование как предсказателя, так и ответа | STAT 501» . newonlinecourses.science.psu.edu . Проверено 17 марта 2019 г.
8. Тернер, Хизер (2008). «Введение в обобщенные линейные модели» (PDF) .
9. Ло, Стесон; Эндрюс, Салли (07 августа 2015 г.). «Преобразовать или не трансформировать: использование обобщенных линейных смешанных моделей для анализа данных о времени реакции». Границы в психологии . 6 : 1171. doi : 10.3389/fpsyg.2015.01171 . ISSN  1664-1078. ПМЦ 4528092 . ПМИД  26300841. 
10. «Преобразования: введение». fmwww.bc.edu . Проверено 19 марта 2019 г.
11. Ван Дрогенброк FJ, «Существенная перефразировка закона Ципфа-Мандельброта для решения задач установления авторства с помощью статистики Гаусса» (2019) [1]
12. Ким, Хэ Ён (1 февраля 2013 г.). «Статистические примечания для клинических исследователей: оценка нормального распределения (2) с использованием асимметрии и эксцесса». Восстановительная стоматология и эндодонтия . 38 (1): 52–54. дои : 10.5395/rde.2013.38.1.52. ISSN  2234-7658. ПМЦ 3591587 . ПМИД  23495371. 
13. «Тестирование нормальности, включая асимметрию и эксцесс» . images.mrc-cbu.cam.ac.uk . Проверено 18 марта 2019 г.
14. «Новый взгляд на статистику: непараметрические модели: преобразование рангов». www.sportsci.org . Проверено 23 марта 2019 г.
15. Уортон, Д.; Хуэй, Ф. (2011). «Арксинус ослиный: анализ пропорций в экологии». Экология . 92 (1): 3–10. дои : 10.1890/10-0340.1. hdl : 1885/152287 . ПМИД  21560670.

Внешние ссылки

• Преобразования журнала для асимметричных и широких распределений - обсуждение журнала и преобразований «знакового логарифма» (глава из «Практической науки о данных с R»).