Назначение маршрута , выбор маршрута или назначение трафика касается выбора маршрутов (альтернативно называемых путями) между пунктами отправления и назначения в транспортных сетях . Это четвертый шаг в традиционной модели прогнозирования перевозок после генерации поездок , распределения поездок и выбора режима . Зональный анализ взаимозаменяемости распределения поездок предоставляет таблицы поездок от пункта отправления до пункта назначения. Анализ выбора режима сообщает, какие путешественники будут использовать какой режим . Чтобы определить потребности в объектах, а также затраты и выгоды, нам нужно знать количество путешественников на каждом маршруте и звене сети (маршрут — это просто цепочка связей между пунктом отправления и пунктом назначения). Нам нужно выполнить назначение трафика (или поездки). Предположим, что есть сеть автомагистралей и транзитных систем и предлагаемое дополнение. Сначала мы хотим узнать текущую картину задержки трафика , а затем, что произойдет, если будет сделано дополнение.
Проблема оценки количества пользователей на каждом маршруте существует уже давно. Планировщики начали пристально изучать ее, когда начали строиться автострады и скоростные магистрали. Автострада предлагала более высокий уровень обслуживания по сравнению с местной уличной системой и отводила трафик от местной системы. Сначала методом было отклонение. Использовались соотношения времени в пути, смягченные соображениями затрат, комфорта и уровня обслуживания .
Исследователи Chicago Area Transportation Study (CATS) разработали кривые отклонения для автострад в сравнении с местными улицами. В Калифорнии также было много работы, поскольку у Калифорнии был ранний опыт планирования автострад. В дополнение к работе по отклонению, CATS занялась некоторыми техническими проблемами, которые возникают при работе со сложными сетями. Одним из результатов стал алгоритм Беллмана–Форда–Мура для поиска кратчайших путей в сетях.
Проблема, которую не решал подход к переадресации, заключалась в обратной связи от количества трафика на связях и маршрутах. Если много транспортных средств пытаются использовать объект, объект становится перегруженным , и время в пути увеличивается. В отсутствие какого-либо способа учета обратной связи ранние исследования по планированию (фактически, большинство в период 1960-1975 гг.) игнорировали обратную связь. Они использовали алгоритм Мура для определения кратчайших путей и назначали весь трафик на кратчайшие пути. Это называется назначением «все или ничего», потому что либо весь трафик из i в j движется по маршруту, либо нет.
Назначение пути «все или ничего» или кратчайшего пути не является тривиальным с технико-вычислительной точки зрения. Каждая зона трафика связана с n - 1 зонами, поэтому необходимо рассмотреть множество путей. Кроме того, в конечном итоге нас интересует трафик на звеньях. Звено может быть частью нескольких путей, и трафик на путях должен суммироваться звено за звеном.
Можно привести аргумент в пользу подхода «все или ничего». Он выглядит следующим образом: исследование планирования направлено на поддержку инвестиций, чтобы на всех линиях был доступен хороший уровень обслуживания. Используя время в пути, связанное с запланированным уровнем обслуживания, расчеты показывают, как будет проходить трафик после внедрения улучшений. Зная объемы трафика на линиях, можно рассчитать пропускную способность, которая должна быть предоставлена для достижения желаемого уровня обслуживания.
Чтобы учесть влияние загрузки трафика на время в пути и равновесие трафика, было разработано несколько эвристических процедур расчета. Одна эвристика действует пошагово. Трафик, который должен быть назначен, делится на части (обычно 4). Назначается первая часть трафика. Вычисляется новое время в пути и назначается следующая часть трафика. Последний шаг повторяется до тех пор, пока не будет назначен весь трафик. CATS использовала вариацию этого; она назначала строку за строкой в таблице OD.
Эвристика, включенная в коллекцию компьютерных программ FHWA , действует по-другому.
Эти процедуры, похоже, работают «довольно хорошо», но они не точны.
Dafermos (1968) применил алгоритм Frank-Wolfe (1956, Florian 1976), который можно использовать для решения проблемы равновесия трафика. Предположим, что мы рассматриваем сеть автомагистралей. Для каждого звена есть функция, устанавливающая связь между сопротивлением и объемом трафика. Бюро общественных дорог (BPR) разработало функцию перегрузки звена (дуги) (или задержку объема, или производительность звена), которую мы будем называть S a (v a )
Существуют и другие функции перегрузки. CATS долгое время использовала функцию, отличную от той, что используется BPR, но, похоже, результаты при сравнении функций CATS и BPR мало чем отличаются.
Чтобы распределить трафик по путям и ссылкам, нам нужны правила, и существуют известные условия равновесия Уордропа . [1] Суть их в том, что путешественники будут стремиться найти кратчайший (с наименьшим сопротивлением) путь от отправной точки до пункта назначения, а равновесие сети наступает, когда ни один путешественник не может уменьшить усилия по путешествию, перейдя на новый путь. Это называется оптимальными условиями для пользователя, поскольку ни один пользователь не выиграет от изменения путей путешествия, когда система находится в равновесии.
Оптимальное равновесие пользователя можно найти, решив следующую задачу нелинейного программирования:
при условии:
где - количество транспортных средств на пути r от пункта отправления i до пункта назначения j . Таким образом, ограничение (2) говорит, что все поездки должны иметь место – i = 1 ... n; j = 1 ... n
= 1, если ссылка a находится на пути r от i до j; ноль в противном случае. Таким образом, ограничение (1) суммирует трафик на каждой ссылке. Для каждой ссылки в сети есть ограничение. Ограничение (3) гарантирует отсутствие отрицательного трафика.
Пример из Eash, Janson и Boyce (1979) проиллюстрирует решение нелинейной программной задачи. Есть две связи от узла 1 до узла 2, и есть функция сопротивления для каждой связи (см. Рисунок 1). Области под кривыми на рисунке 2 соответствуют интегрированию от 0 до a в уравнении 1, их сумма составляет 220 674. Обратите внимание, что функция для связи b построена в обратном направлении.
Рисунок 1: Двухмаршрутная сеть

Рисунок 2: Графическое решение задачи назначения равновесия
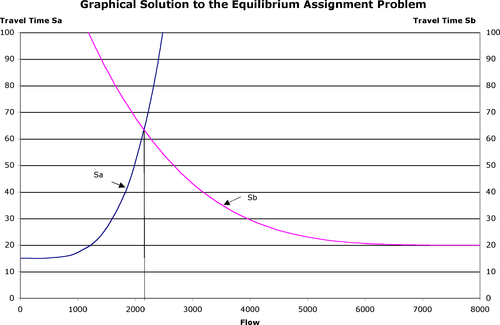
Рисунок 3: Распределение транспортных средств, не удовлетворяющее условию равновесия

В состоянии равновесия на линии а находится 2152 транспортных средства , а на линии b — 5847. Время в пути одинаково на каждом маршруте: около 63.
Рисунок 3 иллюстрирует распределение транспортных средств, которое не соответствует равновесному решению. Кривые не изменились. Но при новом распределении транспортных средств по маршрутам затененная область должна быть включена в решение, поэтому решение на рисунке 3 больше решения на рисунке 2 на площадь затененной области.
Модель планирования городского транспорта развивалась как набор шагов, которым нужно следовать, и модели развивались для использования на каждом шаге. Иногда были шаги внутри шагов, как в случае с первым утверждением модели Лоури . В некоторых случаях было отмечено, что шаги могут быть интегрированы. В более общем плане шаги абстрагируются от решений, которые могут быть приняты одновременно, и было бы желательно лучше воспроизвести это в анализе.
Модели дезагрегированного спроса были впервые разработаны для решения проблемы выбора способа передвижения. Эта проблема предполагает, что человек решил отправиться в путешествие, куда он отправится и в какое время он будет совершаться. Они использовались для решения подразумеваемого более широкого контекста. Обычно разрабатывается вложенная модель, например, начиная с вероятности совершения поездки, затем изучая выбор мест, а затем выбор способа передвижения. Время путешествия обрабатывать немного сложнее.
Модель энтропии с двойным ограничением Уилсона стала отправной точкой для усилий на совокупном уровне. Эта модель содержит ограничение
где — стоимость перемещения по каналу, относится к трафику по каналу, а C — ограничение ресурса, которое должно быть установлено при подгонке модели с данными. Вместо использования этой формы ограничения можно использовать монотонно возрастающую функцию сопротивления, используемую при назначении трафика. Результат определяет перемещения из зоны в зону и назначает трафик сетям, и это имеет большой смысл с точки зрения того, как можно представить себе работу системы — трафик из зоны в зону зависит от сопротивления, вызванного перегрузкой.
В качестве альтернативы функция сопротивления связи может быть включена в целевую функцию (а функция общей стоимости исключена из ограничений).
Обобщенный дезагрегированный выборный подход развился, как и обобщенный агрегатный подход. Большой вопрос заключается в отношениях между ними. Когда мы используем макромодель, мы хотели бы знать дезагрегированное поведение, которое она представляет. Если мы проводим микроанализ, мы хотели бы знать агрегированные последствия анализа.
Уилсон выводит модель, подобную гравитации , с весовыми параметрами, которые говорят что-то о привлекательности пунктов отправления и назначения. Без лишней математики мы можем записать утверждения о вероятности выбора, основанные на привлекательности, и они принимают форму, похожую на некоторые разновидности моделей дезагрегированного спроса.
Давно признано, что спрос на поездки зависит от предложения сети. Пример открытия нового моста там, где его раньше не было, что приводит к дополнительному трафику, отмечался на протяжении столетий. Много исследований было направлено на разработку методов, позволяющих системе прогнозирования напрямую учитывать это явление. Эванс (1974) опубликовал докторскую диссертацию о математически строгом сочетании модели распределения гравитации с моделью равновесного назначения. Самая ранняя ссылка на эту интеграцию — работа Ирвина и Фон Куба, о которой сообщают Флориан и др. (1975), которые комментируют работу Эванса:
«Работа Эванса чем-то напоминает алгоритмы, разработанные Ирвином и Фон Кьюбом [«Ограничение пропускной способности в программах назначения многопутевого режима» Бюллетень HRB 347 (1962)] для транспортного исследования Торонто . Их работа допускает обратную связь между перегруженным назначением и распределением поездок, хотя они применяют последовательные процедуры. Начиная с начального решения проблемы распределения, межзональные поездки назначаются на начальные кратчайшие маршруты. Для последовательных итераций вычисляются новые кратчайшие маршруты, и их длины используются в качестве времени доступа для ввода модели распределения. Затем новые межзональные потоки назначаются в некоторой пропорции к уже найденным маршрутам. Процедура останавливается, когда межзональное время для последовательных итераций становится почти равным».
Флориан и др. предложили несколько иной метод решения комбинированного распределения, применяя непосредственно алгоритм Франка-Вульфа. Бойс и др. (1988) обобщают исследования по проблемам равновесия сети, включая распределение с эластичным спросом.
Задача с тремя связями не может быть решена графически, а большинство задач транспортной сети включают большое количество узлов и связей. Например, Иш и др. изучали дорожную сеть в округе ДюПейдж, где было около 30 000 односторонних связей и 9 500 узлов. Поскольку задачи большие, для решения задачи назначения необходим алгоритм, и используется алгоритм Фрэнка-Вульфа (с различными современными модификациями с момента первой публикации). Начните с назначения «все или ничего», а затем следуйте правилу, разработанному Фрэнком-Вульфом, чтобы итерироваться к минимальному значению целевой функции. (Алгоритм применяет последовательные допустимые решения для достижения сходимости к оптимальному решению. Он использует эффективную процедуру поиска для быстрого перемещения вычисления к оптимальному решению.) Время в пути соответствует двойственным переменным в этой задаче программирования.
Интересно, что алгоритм Франка-Вульфа был доступен в 1956 году. Его применение было разработано в 1968 году, и потребовалось еще почти два десятилетия, прежде чем первый алгоритм назначения равновесия был внедрен в широко используемое программное обеспечение для планирования перевозок (Emme и Emme/2, разработанные Флорианом и другими в Монреале). Мы не хотели бы делать никаких общих выводов из медленного наблюдения за применением, главным образом потому, что мы можем найти обратные примеры о темпах и закономерностях развития техники. Например, симплексный метод для решения задач линейного программирования был разработан и широко применялся до разработки большей части теории программирования.
Постановка задачи и алгоритм имеют общее применение в гражданском строительстве — гидравлике, конструкциях и строительстве. (См. Хендриксон и Дженсон, 1984).
Модели назначения маршрутов основаны, по крайней мере, в некоторой степени на эмпирических исследованиях того, как люди выбирают маршруты в сети . Такие исследования, как правило, сосредоточены на определенном режиме и используют либо заявленные, либо выявленные модели предпочтений .
Было обнаружено, что велосипедисты предпочитают выделенные велосипедные дорожки и избегают крутых холмов. [2]
Общественный транспорт давно рассматривается в контексте назначения маршрута [3] , и было проведено много исследований по выбору маршрута транзита. Среди прочих факторов, пользователи транзита пытаются минимизировать общее время в пути, время или расстояние пеших прогулок и количество пересадок. [4]