Наименьших квадратов

Метод аппроксимации в статистике

Результат сопоставления набора точек данных квадратичной функцией

Коническая аппроксимация набора точек с использованием приближения наименьших квадратов

Метод наименьших квадратов — это метод оценки параметров в регрессионном анализе , основанный на минимизации суммы квадратов остатков ( остаток — это разница между наблюдаемым значением и подогнанным значением, предоставленным моделью), полученными в результатах каждого отдельного уравнение.

Наиболее важным применением является подбор данных . Когда задача имеет существенные неопределенности в независимой переменной ( переменной x ), тогда возникают проблемы с простой регрессией и методами наименьших квадратов; в таких случаях вместо метода наименьших квадратов можно рассмотреть методологию, необходимую для подбора моделей ошибок в переменных .

Задачи наименьших квадратов делятся на две категории: линейные или обычные наименьшие квадраты и нелинейные наименьшие квадраты , в зависимости от того, являются ли остатки линейными по всем неизвестным. Линейная задача наименьших квадратов возникает в статистическом регрессионном анализе ; оно имеет решение в замкнутой форме . Нелинейная задача обычно решается путем итеративного уточнения ; на каждой итерации система аппроксимируется линейной, поэтому расчет ядра в обоих случаях аналогичен.

Полиномиальный метод наименьших квадратов описывает дисперсию предсказания зависимой переменной как функцию независимой переменной и отклонений от подобранной кривой.

Когда наблюдения происходят из экспоненциального семейства с тождеством в качестве естественной достаточной статистики и мягкими условиями (например, для нормального , экспоненциального , пуассоновского и биномиального распределений ), стандартизированные оценки наименьших квадратов и оценки максимального правдоподобия идентичны. ^[1] Метод наименьших квадратов также можно вывести как метод оценки моментов .

Следующее обсуждение в основном представлено в терминах линейных функций, но использование метода наименьших квадратов допустимо и практично для более общих семейств функций. Кроме того, путем итеративного применения локальной квадратичной аппроксимации к вероятности (с помощью информации Фишера ) можно использовать метод наименьших квадратов для подбора обобщенной линейной модели .

Метод наименьших квадратов был официально открыт и опубликован Адрианом -Мари Лежандром (1805 г.), ^[2] хотя обычно его также приписывают Карлу Фридриху Гауссу (1809 г.), ^{[3] [4]} , который внес значительный теоретический прогресс в метод ^[4] и, возможно, также использовал его в своих более ранних работах в 1794 и 1795 годах. ^{[5] [4]}

История

Основание

Метод наименьших квадратов вырос из областей астрономии и геодезии , когда ученые и математики стремились найти решения проблем навигации по океанам Земли в эпоху Великих географических открытий . Точное описание поведения небесных тел было ключом к тому, чтобы корабли могли плавать в открытом море, где моряки больше не могли полагаться на наземные наблюдения для навигации.

Этот метод стал кульминацией нескольких достижений, произошедших в восемнадцатом веке: ^[6]

• Комбинация различных наблюдений как лучшая оценка истинного значения; ошибки уменьшаются с агрегированием, а не увеличиваются, возможно, впервые это выразил Роджер Коутс в 1722 году.
• Сочетание различных наблюдений, проведенных в одних и тех же условиях, противоречит простому стремлению максимально точно наблюдать и записывать одно наблюдение. Этот подход был известен как метод средних значений. Этот подход особенно использовался Тобиасом Майером при изучении либраций Луны в 1750 году и Пьером-Симоном Лапласом в его работе по объяснению различий в движении Юпитера и Сатурна в 1788 году.
• Сочетание разных наблюдений, сделанных в разных условиях. Этот метод стал известен как метод наименьшего абсолютного отклонения . В частности, его выполнили Роджер Джозеф Боскович в своей работе о форме Земли в 1757 году и Пьер-Симон Лаплас для той же задачи в 1789 и 1799 годах.
• Разработка критерия, который можно оценить, чтобы определить, когда было достигнуто решение с минимальной ошибкой. Лаплас попытался указать математическую форму плотности вероятности ошибок и определить метод оценки, который минимизирует ошибку оценки. Для этой цели Лаплас использовал симметричное двустороннее экспоненциальное распределение, которое мы теперь называем распределением Лапласа, для моделирования распределения ошибок, и использовал сумму абсолютных отклонений в качестве ошибки оценки. Он считал, что это самые простые предположения, которые он мог сделать, и надеялся получить среднее арифметическое как наилучшую оценку. Вместо этого его оценкой была задняя медиана.

Метод

Карл Фридрих Гаусс

Первое четкое и краткое изложение метода наименьших квадратов было опубликовано Лежандром в 1805 году. ^[7] Этот метод описывается как алгебраическая процедура подгонки линейных уравнений к данным, и Лежандр демонстрирует новый метод, анализируя те же данные, что и Лаплас, для форму Земли. В течение десяти лет после публикации Лежандра метод наименьших квадратов был принят в качестве стандартного инструмента астрономии и геодезии во Франции, Италии и Пруссии, что представляет собой чрезвычайно быстрое признание научной техники. ^[6]

В 1809 году Карл Фридрих Гаусс опубликовал свой метод расчета орбит небесных тел. В этой работе он утверждал, что владеет методом наименьших квадратов с 1795 года. ^[8] Это, естественно, привело к спору о приоритете с Лежандром. Однако, надо отдать должное Гауссу, он пошел дальше Лежандра и сумел связать метод наименьших квадратов с принципами вероятности и с нормальным распределением . Ему удалось завершить программу Лапласа по определению математической формы плотности вероятности наблюдений в зависимости от конечного числа неизвестных параметров и определить метод оценки, минимизирующий ошибку оценки. Гаусс показал, что среднее арифметическое действительно является лучшей оценкой параметра местоположения за счет изменения как плотности вероятности , так и метода оценки. Затем он перевернул проблему, задав вопрос, какую форму должна иметь плотность и какой метод оценки следует использовать, чтобы получить среднее арифметическое как оценку параметра местоположения. В этой попытке он изобрел нормальное распределение.

Первая демонстрация силы метода Гаусса произошла, когда он использовался для предсказания будущего местоположения недавно открытого астероида Церера . 1 января 1801 года итальянский астроном Джузеппе Пиацци открыл Цереру и смог отслеживать ее путь в течение 40 дней, прежде чем она потерялась в ярком свете Солнца. На основе этих данных астрономы хотели определить местоположение Цереры после того, как она вышла из-за Солнца, не решая сложные нелинейные уравнения движения планет Кеплера . Единственные предсказания, которые успешно позволили венгерскому астроному Францу Ксаверу фон Заку переместить Цереру, были предсказания, сделанные 24-летним Гауссом с использованием анализа наименьших квадратов.

В 1810 году, прочитав работу Гаусса, Лаплас, доказав центральную предельную теорему , использовал ее для большого выборочного обоснования метода наименьших квадратов и нормального распределения. В 1822 году Гаусс смог заявить, что подход к регрессионному анализу методом наименьших квадратов является оптимальным в том смысле, что в линейной модели, где ошибки имеют нулевое среднее значение, некоррелированы и имеют равные дисперсии, лучшая линейная несмещенная оценка коэффициенты - это метод наименьших квадратов. Этот результат известен как теорема Гаусса–Маркова .

Идея анализа методом наименьших квадратов была также независимо сформулирована американцем Робертом Адрейном в 1808 году. В последующие два столетия исследователи теории ошибок и статистики нашли множество различных способов реализации метода наименьших квадратов. ^[9]

Постановка задачи

Цель состоит в корректировке параметров модельной функции для наилучшего соответствия набору данных. Простой набор данных состоит из n точек (пар данных) , i = 1, …, n , где — независимая переменная , а — зависимая переменная, значение которой находится путем наблюдения. Модельная функция имеет вид , где в векторе содержатся m регулируемых параметров . Цель состоит в том, чтобы найти значения параметров модели, которые «наилучшим образом» соответствуют данным. Соответствие модели точке данных измеряется ее остатком , определяемым как разница между наблюдаемым значением зависимой переменной и значением, предсказанным моделью: ${\displaystyle (x_{i},y_{i})\!}$ ${\displaystyle x_{i}\!}$ ${\displaystyle y_{i}\!}$ ${\displaystyle f(x,{\boldsymbol {\beta }})}$ ${\displaystyle {\boldsymbol {\beta }}}$

${\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }}).}$

Остатки отображаются в зависимости от соответствующих значений. Случайные колебания указывают на то, что линейная модель подходит. ${\displaystyle x}$ ${\displaystyle r_{i}=0}$

Метод наименьших квадратов находит оптимальные значения параметров путем минимизации суммы квадратов остатков , : ^[10] ${\displaystyle S}$

${\displaystyle S=\sum _{i=1}^{n}r_{i}^{2}.}$

В простейшем случае результатом метода наименьших квадратов является среднее арифметическое входных данных. ${\displaystyle f(x_{i},{\boldsymbol {\beta }})=\beta }$

Примером модели в двух измерениях является модель прямой линии. Обозначая y-пересечение как и наклон как , модельная функция определяется как . См. линейный метод наименьших квадратов для получения полностью проработанного примера этой модели. ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$ ${\displaystyle f(x,{\boldsymbol {\beta }})=\beta _{0}+\beta _{1}x}$

Точка данных может состоять из более чем одной независимой переменной. Например, при подгонке плоскости к набору измерений высоты плоскость является функцией двух независимых переменных, скажем, x и z . В самом общем случае в каждой точке данных может быть одна или несколько независимых переменных и одна или несколько зависимых переменных.

Справа находится остаточный график, иллюстрирующий случайные колебания значения , что указывает на то, что линейная модель подходит. является независимой случайной величиной. ^[10] ${\displaystyle r_{i}=0}$ ${\displaystyle (Y_{i}=\alpha +\beta x_{i}+U_{i})}$ ${\displaystyle U_{i}}$  

Остатки отображаются в зависимости от соответствующих значений. Параболическая форма колебаний указывает на то, что параболическая модель подходит. ${\displaystyle x}$ ${\displaystyle r_{i}=0}$

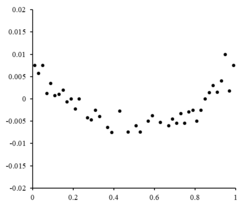
Если бы остаточные точки имели какую-то форму и не колебались случайным образом, линейная модель не была бы подходящей. Например, если остаточный график имел параболическую форму, как показано справа, для данных подойдет параболическая модель. Остатки для параболической модели можно рассчитать через . ^[10] ${\displaystyle (Y_{i}=\alpha +\beta x_{i}+\gamma x_{i}^{2}+U_{i})}$ ${\displaystyle r_{i}=y_{i}-{\hat {\alpha }}-{\hat {\beta }}x_{i}-{\widehat {\gamma }}x_{i}^{2}}$

Ограничения

Эта формулировка регрессии учитывает только ошибки наблюдения в зависимой переменной (но альтернативная регрессия общих наименьших квадратов может учитывать ошибки в обеих переменных). Есть два довольно разных контекста с разными последствиями:

• Регрессия для прогнозирования. Здесь модель подбирается так, чтобы обеспечить правило прогнозирования для применения в аналогичной ситуации, к которой применимы данные, использованные для подгонки. Здесь зависимые переменные, соответствующие такому будущему применению, будут подвержены тем же типам ошибок наблюдения, что и данные, используемые для подбора. Поэтому логически логично использовать для таких данных правило прогнозирования по методу наименьших квадратов.
• Регрессия для установления «истинных отношений». В стандартном регрессионном анализе , который приводит к аппроксимации методом наименьших квадратов, существует неявное предположение, что ошибки в независимой переменной равны нулю или строго контролируются, чтобы ими можно было пренебречь. Когда ошибки в независимой переменной не пренебрежимо малы, можно использовать модели ошибок измерения ; такие методы могут привести к оценкам параметров , проверке гипотез и доверительным интервалам , которые учитывают наличие ошибок наблюдения в независимых переменных. ^[11] Альтернативный подход заключается в подборе модели методом наименьших квадратов ; это можно рассматривать как прагматичный подход к балансированию эффектов различных источников ошибок при формулировании целевой функции для использования при подборе модели.

Решение задачи наименьших квадратов

Минимум суммы квадратов находится путем установки градиента равным нулю. Поскольку модель содержит m параметров, существует m уравнений градиента:

$${\displaystyle {\frac {\partial S}{\partial \beta _{j}}}=2\sum _{i}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m,}$$

${\displaystyle r_{i}=y_{i}-f(x_{i},{\boldsymbol {\beta }})}$

$${\displaystyle -2\sum _{i}r_{i}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}=0,\ j=1,\ldots ,m.}$$

Уравнения градиента применимы ко всем задачам наименьших квадратов. Каждая конкретная проблема требует определенных выражений для модели и ее частных производных . ^[12]

Линейный метод наименьших квадратов

Модель регрессии является линейной, если модель содержит линейную комбинацию параметров, т. е.

$${\displaystyle f(x,{\boldsymbol {\beta }})=\sum _{j=1}^{m}\beta _{j}\phi _{j}(x),}$$

^[12] ${\displaystyle \phi _{j}}$ ${\displaystyle x}$

Полагая и помещая независимые и зависимые переменные в матрицы и соответственно, мы можем вычислить наименьшие квадраты следующим образом. Обратите внимание, что это набор всех данных. ^{[12] [13]} ${\displaystyle X_{ij}=\phi _{j}(x_{i})}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle D}$

$${\displaystyle L(D,{\boldsymbol {\beta }})=\left\|Y-X{\boldsymbol {\beta }}\right\|^{2}=(Y-X{\boldsymbol {\beta }})^{\mathsf {T}}(Y-X{\boldsymbol {\beta }})=Y^{\mathsf {T}}Y-Y^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$

Градиент потерь составляет:

$${\displaystyle {\frac {\partial L(D,{\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\frac {\partial \left(Y^{\mathsf {T}}Y-Y^{\mathsf {T}}X{\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}Y+{\boldsymbol {\beta }}^{\mathsf {T}}X^{\mathsf {T}}X{\boldsymbol {\beta }}\right)}{\partial {\boldsymbol {\beta }}}}=-2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$

Приравнивая градиент потерь к нулю и решая для , получаем: ^{[13] [12]} ${\displaystyle {\boldsymbol {\beta }}}$

$${\displaystyle -2X^{\mathsf {T}}Y+2X^{\mathsf {T}}X{\boldsymbol {\beta }}=0\Rightarrow X^{\mathsf {T}}Y=X^{\mathsf {T}}X{\boldsymbol {\beta }}}$$

$${\displaystyle {\boldsymbol {\hat {\beta }}}=\left(X^{\mathsf {T}}X\right)^{-1}X^{\mathsf {T}}Y}$$

Нелинейный метод наименьших квадратов

В некоторых случаях существует решение в замкнутой форме нелинейной задачи наименьших квадратов, но в целом его нет. В случае отсутствия решения в замкнутой форме для нахождения значения параметров, минимизирующего цель, используются численные алгоритмы. Большинство алгоритмов предполагают выбор начальных значений параметров. Далее параметры уточняются итерационно, то есть значения получаются методом последовательного приближения: ${\displaystyle \beta }$

$${\displaystyle {\beta _{j}}^{k+1}={\beta _{j}}^{k}+\Delta \beta _{j},}$$

kв ряд Тейлора ${\displaystyle \Delta \beta _{j}}$ ${\displaystyle {\boldsymbol {\beta }}^{k}}$

$${\displaystyle {\begin{aligned}f(x_{i},{\boldsymbol {\beta }})&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}{\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}\left(\beta _{j}-{\beta _{j}}^{k}\right)\\&=f^{k}(x_{i},{\boldsymbol {\beta }})+\sum _{j}J_{ij}\,\Delta \beta _{j}.\end{aligned}}}$$

Якобиан J является функцией констант, независимой переменной и параметров, поэтому он меняется от одной итерации к другой . Остатки определяются как

$${\displaystyle r_{i}=y_{i}-f^{k}(x_{i},{\boldsymbol {\beta }})-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}=\Delta y_{i}-\sum _{j=1}^{m}J_{ij}\,\Delta \beta _{j}.}$$

Чтобы минимизировать сумму квадратов , уравнение градиента устанавливается равным нулю и решается для : ${\displaystyle r_{i}}$ ${\displaystyle \Delta \beta _{j}}$

$${\displaystyle -2\sum _{i=1}^{n}J_{ij}\left(\Delta y_{i}-\sum _{k=1}^{m}J_{ik}\,\Delta \beta _{k}\right)=0,}$$

в mнормальных уравнений

$${\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{m}J_{ij}J_{ik}\,\Delta \beta _{k}=\sum _{i=1}^{n}J_{ij}\,\Delta y_{i}\qquad (j=1,\ldots ,m).}$$

Нормальные уравнения записываются в матричной записи как

$${\displaystyle \left(\mathbf {J} ^{\mathsf {T}}\mathbf {J} \right)\Delta {\boldsymbol {\beta }}=\mathbf {J} ^{\mathsf {T}}\Delta \mathbf {y} .}$$

Это определяющие уравнения алгоритма Гаусса–Ньютона .

Различия между линейным и нелинейным методом наименьших квадратов

• Модельная функция f в LLSQ (линейный метод наименьших квадратов) представляет собой линейную комбинацию параметров формы. Модель может представлять собой прямую линию, параболу или любую другую линейную комбинацию функций. В NLLSQ (нелинейный метод наименьших квадратов) параметры представлены в виде функций, таких как и т. д. Если производные либо постоянны, либо зависят только от значений независимой переменной, модель линейна по параметрам. В противном случае модель нелинейна. ${\displaystyle f=X_{i1}\beta _{1}+X_{i2}\beta _{2}+\cdots }$ ${\displaystyle \beta ^{2},e^{\beta x}}$ ${\displaystyle \partial f/\partial \beta _{j}}$
• Нужны начальные значения параметров, чтобы найти решение проблемы NLLSQ; LLSQ не требует их.
• Алгоритмы решения NLLSQ часто требуют, чтобы якобиан можно было вычислить аналогично LLSQ. Аналитические выражения для частных производных могут быть сложными. Если аналитические выражения невозможно получить, либо частные производные должны быть рассчитаны путем численной аппроксимации, либо должна быть сделана оценка якобиана, часто с помощью конечных разностей .
• Несходимость (неспособность алгоритма найти минимум) — обычное явление в NLLSQ.
• LLSQ глобально вогнут, поэтому несходимость не является проблемой.
• Решение NLLSQ обычно представляет собой итерационный процесс, который необходимо прекратить, когда выполняется критерий сходимости. Решения LLSQ можно вычислить с использованием прямых методов, хотя задачи с большим количеством параметров обычно решаются итерационными методами, такими как метод Гаусса – Зейделя .
• В LLSQ решение уникально, но в NLLSQ может быть несколько минимумов суммы квадратов.
• При условии, что ошибки не коррелируют с переменными-предикторами, LLSQ дает несмещенные оценки, но даже при этом условии оценки NLLSQ обычно являются смещенными.

Эти различия необходимо учитывать всякий раз, когда ищется решение нелинейной задачи наименьших квадратов. ^[12]

Пример

Рассмотрим простой пример из физики. Пружина должна подчиняться закону Гука, который гласит, что растяжение пружины y пропорционально приложенной к ней силе F.

${\displaystyle y=f(F,k)=kF\!}$

представляет собой модель, где F — независимая переменная. Чтобы оценить силовую константу k , мы проводим серию из n измерений с различными силами для получения набора данных, где y _i — измеренное растяжение пружины. ^[14] Каждое экспериментальное наблюдение будет содержать некоторую ошибку, и поэтому мы можем указать эмпирическую модель для наших наблюдений: ${\displaystyle (F_{i},y_{i}),\ i=1,\dots ,n\!}$ ${\displaystyle \varepsilon }$

${\displaystyle y_{i}=kF_{i}+\varepsilon _{i}.\,}$

Существует множество методов, которые мы могли бы использовать для оценки неизвестного параметра k . Поскольку n уравнений с m переменными в наших данных представляют собой переопределенную систему с одним неизвестным и n уравнениями, мы оцениваем k с помощью метода наименьших квадратов. Сумма квадратов, которые необходимо минимизировать, равна

${\displaystyle S=\sum _{i=1}^{n}(y_{i}-kF_{i})^{2}.}$^[12]

Оценка силовой постоянной k по методу наименьших квадратов определяется выражением

${\displaystyle {\hat {k}}={\frac {\sum _{i}F_{i}y_{i}}{\sum _{i}F_{i}^{2}}}.}$

Мы предполагаем, что приложение силы заставляет пружину расширяться. После получения силовой константы методом наименьших квадратов мы прогнозируем расширение на основе закона Гука.

Количественная оценка неопределенности

При расчете методом наименьших квадратов с единичными весами или в линейной регрессии отклонение j -го параметра, обозначаемого , обычно оценивается с помощью ${\displaystyle \operatorname {var} ({\hat {\beta }}_{j})}$

${\displaystyle \operatorname {var} ({\hat {\beta }}_{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{-1}\right)_{jj}\approx {\hat {\sigma }}^{2}C_{jj},}$

${\displaystyle {\hat {\sigma }}^{2}\approx {\frac {S}{n-m}}}$

${\displaystyle C=\left(X^{\mathsf {T}}X\right)^{-1},}$

где истинная дисперсия ошибок σ ² заменяется оценкой, приведенной статистикой хи-квадрат , основанной на минимизированном значении остаточной суммы квадратов (целевая функция), S . Знаменатель n  −  m представляет собой статистические степени свободы ; см. эффективные степени свободы для обобщений. ^[12] C — ковариационная матрица .

Статистическое тестирование

Если известно распределение вероятностей параметров или сделано асимптотическое приближение, можно найти доверительные пределы . Аналогично, статистические тесты остатков могут проводиться, если распределение вероятностей остатков известно или предполагается. Мы можем получить распределение вероятностей любой линейной комбинации зависимых переменных, если известно или предполагается распределение вероятностей экспериментальных ошибок. Сделать вывод легко, если предположить, что ошибки подчиняются нормальному распределению, что, следовательно, подразумевает, что оценки параметров и остатки также будут нормально распределяться в зависимости от значений независимых переменных. ^[12]

Для статистической проверки результатов необходимо сделать предположения о характере экспериментальных ошибок. Распространенным предположением является то, что ошибки принадлежат нормальному распределению. Центральная предельная теорема подтверждает идею о том, что во многих случаях это хорошее приближение.

• Теорема Гаусса –Маркова . В линейной модели, в которой ошибки имеют нулевое ожидание , обусловленное независимыми переменными, некоррелированы и имеют равные дисперсии , лучшей линейной несмещенной оценкой любой линейной комбинации наблюдений является ее оценка методом наименьших квадратов. «Лучший» означает, что оценки параметров по методу наименьших квадратов имеют минимальную дисперсию. Предположение о равной дисперсии справедливо, когда все ошибки принадлежат одному и тому же распределению. ^[15]
• Если ошибки принадлежат нормальному распределению, оценки методом наименьших квадратов также являются оценками максимального правдоподобия в линейной модели.

Однако предположим, что ошибки не распределены нормально. В этом случае центральная предельная теорема , тем не менее, часто подразумевает, что оценки параметров будут примерно нормально распределены, пока выборка достаточно велика. По этой причине, учитывая то важное свойство, что среднее значение ошибки не зависит от независимых переменных, распределение члена ошибки не является важной проблемой в регрессионном анализе. В частности, обычно не важно, соответствует ли член ошибки нормальному распределению.

Взвешенные наименьшие квадраты

Эффект «разветвления» гетероскедастичности

Особый случай обобщенного метода наименьших квадратов , называемый взвешенным методом наименьших квадратов, возникает, когда все недиагональные элементы Ω (корреляционная матрица остатков) равны нулю; дисперсии наблюдений (вдоль диагонали ковариационной матрицы) все еще могут быть неравными ( гетероскедастичность ) . Проще говоря, гетероскедастичность — это когда дисперсия зависит от значения, которое приводит к тому, что остаточный график создает эффект «разветвления» в сторону больших значений, как видно на остаточном графике справа. С другой стороны, гомоскедастичность предполагает, что дисперсия и дисперсия равны. ^[10] ${\displaystyle Y_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle Y_{i}}$ ${\displaystyle Y_{i}}$ ${\displaystyle U_{i}}$  

Связь с основными компонентами

Первый главный компонент среднего значения набора точек может быть представлен той линией, которая наиболее близко приближается к точкам данных (измеряется квадратом расстояния наибольшего сближения, т.е. перпендикулярно линии). Напротив, линейный метод наименьших квадратов пытается минимизировать расстояние только в направлении. Таким образом, хотя они используют одинаковую метрику ошибок, линейный метод наименьших квадратов — это метод, который преимущественно обрабатывает одно измерение данных, в то время как PCA одинаково обрабатывает все измерения. ${\displaystyle y}$

Связь с теорией меры

Известный статистик Сара ван де Гир использовала теорию эмпирических процессов и размерность Вапника – Червоненкиса, чтобы доказать, что оценку методом наименьших квадратов можно интерпретировать как меру в пространстве функций, интегрируемых с квадратом . ^[16]

Регуляризация

Тихоновская регуляризация

В некоторых контекстах регуляризованная версия решения методом наименьших квадратов может быть предпочтительнее. Регуляризация Тихонова (или регрессия гребня ) добавляет ограничение, что квадрат нормы вектора параметров не превышает заданное значение к формулировке метода наименьших квадратов, что приводит к ограниченной проблеме минимизации. Это эквивалентно задаче неограниченной минимизации, где целевая функция представляет собой остаточную сумму квадратов плюс штрафной член и является параметром настройки (это лагранжева форма задачи ограниченной минимизации). ^[17] ${\displaystyle \|\beta \|_{2}^{2}}$ ${\displaystyle \ell _{2}}$ ${\displaystyle \alpha \|\beta \|_{2}^{2}}$ ${\displaystyle \alpha }$

В байесовском контексте это эквивалентно помещению нулевого среднего, нормально распределенного, в вектор вектора параметров.

Метод Лассо

Альтернативной регуляризованной версией метода наименьших квадратов является «Лассо» (оператор наименьшего абсолютного сокращения и выбора), который использует ограничение , согласно которому L 1 -норма вектора параметров не превышает заданного значения. ^{[18] [19] [20]} (Можно показать, как указано выше, используя множители Лагранжа, что это эквивалентно неограниченной минимизации штрафа по методу наименьших квадратов с добавлением.) В байесовском контексте это эквивалентно размещению нулевого среднего Априорное распределение Лапласа на векторе параметров. ^[21] Задача оптимизации может быть решена с использованием квадратичного программирования или более общих методов выпуклой оптимизации , а также с помощью конкретных алгоритмов, таких как алгоритм регрессии наименьшего угла . ${\displaystyle \|\beta \|_{1}}$ ${\displaystyle \alpha \|\beta \|_{1}}$

Одно из основных отличий между Лассо и гребневой регрессией заключается в том, что в гребневой регрессии по мере увеличения штрафа все параметры уменьшаются, оставаясь при этом ненулевыми, в то время как в Лассо увеличение штрафа приведет к тому, что все больше и больше параметров будут становиться ненулевыми. доведен до нуля. Это преимущество Лассо перед гребневой регрессией, поскольку приведение параметров к нулю отменяет выбор объектов из регрессии. Таким образом, Лассо автоматически выбирает более релевантные функции и отбрасывает остальные, тогда как регрессия Риджа никогда полностью не отбрасывает какие-либо функции. Некоторые методы выбора признаков разработаны на основе LASSO, включая Bolasso, который загружает выборки, ^[22] и FeaLect, который анализирует коэффициенты регрессии, соответствующие различным значениям, для оценки всех признаков. ^[23] ${\displaystyle \alpha }$

L ¹ -регуляризованная формулировка полезна в некоторых контекстах из-за ее тенденции отдавать предпочтение решениям, в которых большее количество параметров равно нулю, что дает решения, зависящие от меньшего количества переменных. ^[18] По этой причине «Лассо» и его варианты имеют фундаментальное значение для области сжатого зондирования . Расширением этого подхода является эластичная сетчатая регуляризация .

Смотрите также

• Корректировка по методу наименьших квадратов
• Байесовский оценщик MMSE
• Лучшая линейная несмещенная оценка (СИНИЙ)
• Лучшее линейное несмещенное предсказание (BLUP)
• Теорема Гаусса–Маркова
• Л ₂ норма
• Наименьшие абсолютные отклонения
• Спектральный анализ методом наименьших квадратов
• Погрешность измерения
• Ортогональная проекция
• Проксимальные градиентные методы обучения
• Квадратичная функция потерь
• Среднеквадратичное значение
• Квадратные отклонения от среднего значения

Рекомендации

1. Чарнс, А.; Фром, Эл.; Ю, ПЛ (1976). «Эквивалентность обобщенных наименьших квадратов и оценок максимального правдоподобия в экспоненциальном семействе». Журнал Американской статистической ассоциации . 71 (353): 169–171. дои : 10.1080/01621459.1976.10481508.
2. Мэнсфилд Мерриман, «Список работ, касающихся метода наименьших квадратов»
3. Бретшер, Отто (1995). Линейная алгебра с приложениями (3-е изд.). Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл.
4. Стиглер, Стивен М. (1981). «Гаусс и изобретение метода наименьших квадратов». Анна. Стат . 9 (3): 465–474. дои : 10.1214/aos/1176345451 .
5. Плакетт, Р.Л. (1972). «Открытие метода наименьших квадратов» (PDF) . Биометрика . 59 (2): 239–251.
6. Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. ISBN 978-0-674-40340-6.
7. Лежандр, Адриен-Мари (1805), Nouvelles méthodes pour la détermination des Orbites des comètes [ Новые методы определения орбит комет ] (на французском языке), Париж: Ф. Дидо, hdl : 2027/nyp.33433069112559
8. «Открытие статистической регрессии». Ценаономика . 06.11.2015 . Проверено 4 апреля 2023 г.
9. Олдрич, Дж. (1998). «Выполнение метода наименьших квадратов: перспективы Гаусса и Юла». Международный статистический обзор . 66 (1): 61–81. doi :10.1111/j.1751-5823.1998.tb00406.x. S2CID  121471194.
10. Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель (1946 г.р.). Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. ОСЛК  262680588.{{cite book}}: CS1 maint: others (link)
11. Хорошее введение в ошибки в переменных см. в Fuller, WA (1987). Модели ошибок измерения . Джон Уайли и сыновья. ISBN 978-0-471-86187-4.
12. Уильямс, Джеффри Х. (Джеффри Хью), 1956- (ноябрь 2016 г.). Количественное измерение: тирания чисел . Издательство Morgan & Claypool, Институт физики (Великобритания). Сан-Рафаэль [Калифорния] (40 Oak Drive, Сан-Рафаэль, Калифорния, 94903, США). ISBN 978-1-68174-433-9. ОКЛК  962422324.{{cite book}}: CS1 maint: location (link) CS1 maint: location missing publisher (link) CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
13. Ренчер, Элвин С.; Кристенсен, Уильям Ф. (15 августа 2012 г.). Методы многомерного анализа. Джон Уайли и сыновья. п. 155. ИСБН 978-1-118-39167-9.
14. Гир, Джеймс М. (2013). Механика материалов . Гудно, Барри Дж. (8-е изд.). Стэмфорд, Коннектикут: Cengage Learning. ISBN 978-1-111-57773-5. OCLC  741541348.
15. Халлин, Марк. «Теорема Гаусса-Маркова». Интернет-библиотека Уайли . Энциклопедия окружающей среды . Проверено 18 октября 2023 г.
16. ван де Гир, Сара (июнь 1987 г.). «Новый подход к оценке методом наименьших квадратов с приложениями». Анналы статистики . 15 (2): 587–602. дои : 10.1214/aos/1176350362 . S2CID  123088844.
17. ван Виринген, Вессель Н. (2021). «Конспекты лекций по гребневой регрессии». arXiv : 1509.09169 . {{cite journal}}: Требуется цитировать журнал |journal=( помощь )
18. Тибширани, Р. (1996). «Регрессионное сжатие и отбор с помощью лассо». Журнал Королевского статистического общества, серия B. 58 (1): 267–288. JSTOR  2346178.
19. Хасти, Тревор ; Тибширани, Роберт; Фридман, Джером Х. (2009). Элементы статистического обучения (второе изд.). Спрингер-Верлаг. ISBN 978-0-387-84858-7. Архивировано из оригинала 10 ноября 2009 г.
20. Бюльманн, Питер; ван де Гир, Сара (2011). Статистика для многомерных данных: методы, теория и приложения . Спрингер. ISBN 9783642201929.
21. Парк, Тревор; Казелла, Джордж (2008). «Байесовское лассо». Журнал Американской статистической ассоциации . 103 (482): 681–686. дои : 10.1198/016214508000000337. S2CID  11797924.
22. Бах, Фрэнсис Р. (2008). «Боласо». Материалы 25-й международной конференции по машинному обучению ICML '08 . стр. 33–40. arXiv : 0804.1302 . Бибкод : 2008arXiv0804.1302B. дои : 10.1145/1390156.1390161. ISBN 9781605582054. S2CID  609778.
23. Заре, Хабил (2013). «Оценка релевантности признаков на основе комбинаторного анализа Лассо с применением к диагностике лимфомы». БМК Геномика . 14 (Приложение 1): S14. дои : 10.1186/1471-2164-14-S1-S14 . ПМЦ 3549810 . ПМИД  23369194. 

дальнейшее чтение

• Бьёрк, О. (1996). Численные методы решения задач наименьших квадратов . СИАМ. ISBN 978-0-89871-360-2.
• Кария, Т.; Курата, Х. (2004). Обобщенный метод наименьших квадратов . Хобокен: Уайли. ISBN 978-0-470-86697-9.
• Люенбергер, Д.Г. (1997) [1969]. «Оценка методом наименьших квадратов». Оптимизация методами векторного пространства . Нью-Йорк: Джон Уайли и сыновья. стр. 78–102. ISBN 978-0-471-18117-0.
• Рао, ЧР ; Тутенбург, Х.; и другие. (2008). Линейные модели: метод наименьших квадратов и альтернативы. Серия Спрингера по статистике (3-е изд.). Берлин: Шпрингер. ISBN 978-3-540-74226-5.
• Ван де Мортель, Коэн (апрель 2021 г.). «Многонаправленный регрессионный анализ».
• Вольберг, Дж. (2005). Анализ данных методом наименьших квадратов: извлечение максимальной информации из экспериментов . Берлин: Шпрингер. ISBN 978-3-540-25674-8.

Внешние ссылки

• СМИ, связанные с методом наименьших квадратов, на Викискладе?