Статика — раздел классической механики , занимающийся анализом силы и крутящего момента, действующих на физическую систему , которая не испытывает ускорения , а находится в равновесии с окружающей средой.
Если — сумма сил, действующих на систему, — масса системы, — ускорение системы, второй закон Ньютона гласит, что (жирный шрифт обозначает векторную величину, т.е. имеющую как величину, так и направление ). Если , то . Что касается системы, находящейся в статическом равновесии, ускорение равно нулю, система либо покоится, либо ее центр масс движется с постоянной скоростью .
Применение предположения о нулевом ускорении к суммированию моментов, действующих на систему, приводит к , где — сумма всех моментов, действующих на систему, — момент инерции массы, — угловое ускорение системы. Для системы, где , также верно, что
Вместе уравнения («первое условие равновесия») и («второе условие равновесия») можно использовать для нахождения неизвестных величин, действующих на систему.
Архимед (ок. 287–ок. 212 до н. э.) был пионером в области статики. [1] [2] Более поздние разработки в области статики можно найти в трудах Фивита . [3]
Сила — это действие одного тела на другое. Сила — это либо толчок, либо тяга, и она стремится переместить тело в направлении своего действия. Действие силы характеризуется ее величиной, направлением ее действия и точкой ее приложения (или точкой контакта ). Таким образом, сила — это векторная величина, потому что ее эффект зависит как от направления, так и от величины действия. [4]
Силы классифицируются как контактные или телесные. Контактная сила создается прямым физическим контактом; примером является сила, действующая на тело со стороны опорной поверхности. Телесная сила создается в силу положения тела в силовом поле, таком как гравитационное, электрическое или магнитное поле, и не зависит от контакта с любым другим телом; примером телесной силы является вес тела в гравитационном поле Земли. [5]
Помимо тенденции перемещать тело в направлении своего приложения, сила может также стремиться вращать тело вокруг оси. Ось может быть любой линией, которая не пересекает и не параллельна линии действия силы. Эта тенденция вращения известна как момент силы ( M ). Момент также называется крутящим моментом .
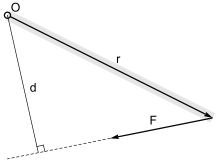
Величина момента силы в точке O равна перпендикулярному расстоянию от O до линии действия силы F , умноженному на величину силы: M = F · d , где
Направление момента задается правилом правой руки, где против часовой стрелки (CCW) — наружу страницы, а по часовой стрелке (CW) — внутрь страницы. Направление момента можно учесть, используя указанное соглашение о знаках, например, знак плюс (+) для моментов против часовой стрелки и знак минус (−) для моментов по часовой стрелке, или наоборот. Моменты можно складывать как векторы.
В векторном формате момент можно определить как векторное произведение радиус-вектора r (вектор от точки O до линии действия) и вектора силы F : [6]
Теорема Вариньона утверждает, что момент силы относительно любой точки равен сумме моментов составляющих силы относительно этой же точки.
Статическое равновесие частицы является важным понятием в статике. Частица находится в равновесии только в том случае, если равнодействующая всех сил, действующих на частицу, равна нулю. В прямоугольной системе координат уравнения равновесия могут быть представлены тремя скалярными уравнениями, где суммы сил во всех трех направлениях равны нулю. Инженерное применение этого понятия заключается в определении натяжения до трех тросов под нагрузкой, например, сил, действующих на каждый трос подъемника, поднимающего объект, или растяжек, удерживающих воздушный шар на земле. [7]
В классической механике момент инерции , также называемый массовым моментом, вращательной инерцией, полярным моментом инерции массы или угловой массой (единицы СИ кг·м²), является мерой сопротивления объекта изменениям его вращения. Это инерция вращающегося тела относительно его вращения. Момент инерции играет во вращательной динамике примерно ту же роль, что и масса в линейной динамике, описывая связь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также несколькими другими величинами. Символы I и J обычно используются для обозначения момента инерции или полярного момента инерции.
В то время как простая скалярная обработка момента инерции достаточна для многих ситуаций, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как вращающиеся волчки и гироскопическое движение.
Это понятие было введено Леонардом Эйлером в его книге 1765 года «Теория движения тел твердых тел» ; он рассмотрел момент инерции и многие связанные с ним концепции, такие как главная ось инерции.
Статика используется при анализе конструкций, например, в архитектурном и строительном проектировании . Сопротивление материалов — это смежная область механики, которая в значительной степени опирается на применение статического равновесия. Ключевым понятием является центр тяжести тела в состоянии покоя: он представляет собой воображаемую точку, в которой находится вся масса тела . Положение точки относительно фундаментов , на которых лежит тело, определяет его устойчивость в ответ на внешние силы. Если центр тяжести находится вне фундаментов, то тело неустойчиво, поскольку действует крутящий момент: любое небольшое возмущение приведет к падению или опрокидыванию тела. Если центр тяжести находится внутри фундаментов, то тело устойчиво, поскольку на тело не действует чистый крутящий момент. Если центр тяжести совпадает с фундаментами, то тело называется метастабильным .
Гидростатика , также известная как статика жидкости , является изучением жидкостей в состоянии покоя (т. е. в статическом равновесии). Характерной чертой любой жидкости в состоянии покоя является то, что сила, действующая на любую частицу жидкости, одинакова во всех точках на одной и той же глубине (или высоте) внутри жидкости. Если результирующая сила больше нуля, жидкость будет двигаться в направлении результирующей силы. Эта концепция была впервые сформулирована в слегка расширенной форме французским математиком и философом Блезом Паскалем в 1647 году и стала известна как закон Паскаля . Она имеет много важных приложений в гидравлике . Архимед , Абу Райхан аль-Бируни , Аль-Хазини [8] и Галилео Галилей также были основными фигурами в развитии гидростатики.
«Используя целый комплекс математических методов (не только унаследованных от античной теории отношений и техники бесконечно малых, но и методы современной алгебры и тонких вычислительных приемов), арабские ученые подняли статику на новый, более высокий уровень. Были обобщены и применены к трехмерным телам классические результаты Архимеда в теории центра тяжести, была основана теория весомого рычага и создана «наука о тяготении», которая впоследствии получила дальнейшее развитие в средневековой Европе. Явления статики изучались с использованием динамического подхода, так что два направления — статика и динамика — оказались взаимосвязанными в рамках единой науки — механики. Соединение динамического подхода с архимедовой гидростатикой породило направление в науке, которое можно назвать средневековой гидродинамикой. [...] Были разработаны многочисленные экспериментальные методы определения удельного веса, основанные, в частности, на теории весов и взвешивания. Классические труды аль-Бируни и аль-Хазини можно считать началом применения экспериментальных методов в средневековой науке .