Модуль

Вычислительная операция

В вычислениях операция деления по модулю возвращает остаток или знаковый остаток от деления после деления одного числа на другое, называемый модулем операции.

Для двух положительных чисел a и n , модуль n (часто сокращенно a mod n ) представляет собой остаток от евклидова деления числа a на n , где a — делимое , а n — делитель . ^[1]

Например, выражение «5 mod 2» даст результат 1, поскольку 5 при делении на 2 даст частное 2 и остаток 1, тогда как выражение «9 mod 3» даст результат 0, поскольку 9 при делении на 3 даст частное 3 и остаток 0.

Хотя обычно выполняется с a и n , оба являющимися целыми числами , многие вычислительные системы теперь допускают другие типы числовых операндов. Диапазон значений для операции целочисленного модуля n составляет от 0 до n − 1 ( mod 1 всегда равен 0; mod 0 не определен, поскольку является делением на ноль ).

Когда хотя бы одно из чисел a или n отрицательно, базовое определение нарушается, и языки программирования различаются в том, как определяются эти значения.

Варианты определения

В математике результатом операции по модулю является класс эквивалентности , и любой член класса может быть выбран в качестве представителя ; однако, обычным представителем является наименьший положительный остаток , наименьшее неотрицательное целое число, принадлежащее этому классу (т. е. остаток от евклидова деления ). ^[2] Однако возможны и другие соглашения. Компьютеры и калькуляторы имеют различные способы хранения и представления чисел; таким образом, их определение операции по модулю зависит от языка программирования или базового оборудования .

Почти во всех вычислительных системах частное q и остаток r от деления a на n удовлетворяют следующим условиям:

Это все еще оставляет неоднозначность знака, если остаток не равен нулю: возможны два варианта для остатка, один отрицательный, а другой положительный; этот выбор определяет, какой из двух последовательных частных должен использоваться для удовлетворения уравнения (1). В теории чисел всегда выбирается положительный остаток, но в вычислениях языки программирования выбирают в зависимости от языка и знаков a или n . ^[a] Например, стандартный Паскаль и АЛГОЛ 68 дают положительный остаток (или 0) даже для отрицательных делителей, а некоторые языки программирования, такие как C90, оставляют это на усмотрение реализации, когда либо n , либо a отрицательны (подробнее см. таблицу в разделе Языки программирования). a по модулю 0 не определено в большинстве систем, хотя некоторые определяют его как a .

• 

   Частное ( q ) и остаток ( r ) как функция делимого ( a ), используя усеченное деление

  Во многих реализациях используется усеченное деление , для которого частное определяется как

  ${\displaystyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$

  где - функция целой части ( округление к нулю ), т.е. усечение до нулевых значащих цифр. Таким образом, согласно уравнению ( 1 ), остаток имеет тот же знак, что и делимое a, поэтому может принимать 2| n | − 1 значений: ${\displaystyle \operatorname {trunc} }$

  ${\displaystyle r=a-n\operatorname {trunc} \left({\frac {a}{n}}\right)}$

• 

  Частное и остаток с использованием дробного деления

  Дональд Кнут ^[3] продвигает метод деления с минимальным дроблением , для которого частное определяется как

  ${\displaystyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$

  где - функция пола ( округление вниз ). Таким образом, согласно уравнению ( 1 ), остаток имеет тот же знак, что и делитель n : ${\displaystyle \lfloor \,\rfloor }$

  ${\displaystyle r=a-n\left\lfloor {\frac {a}{n}}\right\rfloor }$

• 

  Частное и остаток с использованием евклидова деления

  Рэймонд Т. Бут ^[4] продвигает евклидово деление , для которого частное определяется как

  ${\displaystyle q=\operatorname {sgn}(n)\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor ={\begin{cases}\left\lfloor {\frac {a}{n}}\right\rfloor &{\text{if }}n>0\\\left\lceil {\frac {a}{n}}\right\rceil &{\text{if }}n<0\\\end{cases}}}$

  где sgn — функция знака , — функция пола ( округление вниз ), а — функция потолка ( округление вверх ). Таким образом, согласно уравнению ( 1 ), остаток неотрицателен : ${\displaystyle \lfloor \,\rfloor }$ ${\displaystyle \lceil \,\rceil }$

  ${\displaystyle r=a-|n|\left\lfloor {\frac {a}{\left|n\right|}}\right\rfloor }$

• 

  Частное и остаток с использованием округленного деления

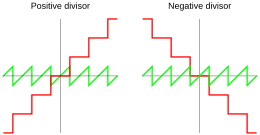
  Common Lisp и IEEE 754 используют округленное деление , для которого частное определяется как

  ${\displaystyle q=\operatorname {round} \left({\frac {a}{n}}\right)}$

  где round — функция округления ( округление половины до четного ). Таким образом, согласно уравнению ( 1 ), остаток попадает между и , а его знак зависит от того, с какой стороны от нуля он попадает в эти границы: ${\displaystyle -{\frac {n}{2}}}$ ${\displaystyle {\frac {n}{2}}}$

  ${\displaystyle r=a-n\operatorname {round} \left({\frac {a}{n}}\right)}$

• 

  Частное и остаток с использованием деления на вершину

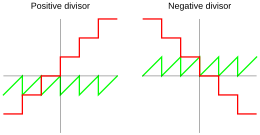
  Common Lisp также использует деление по потолку , для которого частное определяется как

  ${\displaystyle q=\left\lceil {\frac {a}{n}}\right\rceil }$

  где ⌈⌉ — функция потолка ( округление вверх ). Таким образом, согласно уравнению ( 1 ), остаток имеет противоположный знак делителя :

  ${\displaystyle r=a-n\left\lceil {\frac {a}{n}}\right\rceil }$

Если и делимое, и делитель положительны, то усеченное, уменьшенное и евклидово определения согласуются. Если делимое положительно, а делитель отрицателен, то усеченное и евклидово определения согласуются. Если делимое отрицательно, а делитель положительный, то усеченное и евклидово определения согласуются. Если и делимое, и делитель отрицательны, то усеченное и уменьшенное определения согласуются.

Как описывает Лейен,

Бут утверждает, что евклидово деление превосходит другие с точки зрения регулярности и полезных математических свойств, хотя floored delegate, продвигаемое Кнутом, также является хорошим определением. Несмотря на его широкое использование, усеченное деление, как показано, уступает другим определениям.

—  Даан Лейен, «Деление и модуль для компьютерных ученых» ^[5]

Однако усеченное деление удовлетворяет тождеству . ^[6] ${\displaystyle ({-a})/b={-(a/b)}=a/({-b})}$

Обозначение

Некоторые калькуляторы имеют кнопку функции mod() , и многие языки программирования имеют похожую функцию, например, mod( a , n ) . Некоторые также поддерживают выражения, которые используют "%", "mod" или "Mod" в качестве оператора остатка или модуля , например a % nили a mod n.

Для сред, в которых отсутствует подобная функция, можно использовать любое из трех приведенных выше определений.

Распространенные ошибки

Когда результат операции по модулю имеет знак делимого (усеченное определение), это может привести к неожиданным ошибкам.

Например, чтобы проверить, является ли целое число нечетным , можно попробовать проверить, равен ли остаток от деления на 2 1:

bool is_odd ( int n ) { return n % 2 == 1 ; }         

Но в языке, где modulo имеет знак делимого, это неверно, потому что когда n (делимое) отрицательно и нечетно, n mod 2 возвращает −1, а функция возвращает false.

Правильным вариантом является проверка того, что остаток не равен 0 (поскольку остаток 0 одинаков независимо от знаков):

bool is_odd ( int n ) { return n % 2 != 0 ; }         

Проблемы с производительностью

Операции по модулю могут быть реализованы таким образом, что деление с остатком вычисляется каждый раз. Для особых случаев на некоторых аппаратных средствах существуют более быстрые альтернативы. Например, модуль степеней 2 может быть альтернативно выражен как побитовая операция И (предполагая, что x — положительное целое число, или используя необрезающее определение):

x % 2n == x & (2n - 1)

Примеры:

x % 2 == x & 1

x % 4 == x & 3

x % 8 == x & 7

В устройствах и программном обеспечении, которые реализуют побитовые операции более эффективно, чем по модулю, эти альтернативные формы могут привести к более быстрым вычислениям. ^[7]

Оптимизации компилятора могут распознавать выражения вида expression % constant, где constantявляется степенью двойки, и автоматически реализовывать их как expression & (constant-1), позволяя программисту писать более понятный код без ущерба для производительности. Эта простая оптимизация невозможна для языков, в которых результат операции по модулю имеет знак делимого (включая C ), если только делимое не является целочисленным типом без знака . Это связано с тем, что если делимое отрицательно, то и модуль будет отрицательным, тогда как expression & (constant-1)всегда будет положительным. Для этих языков вместо этого необходимо использовать эквивалентность, выраженную с помощью побитовых операций ИЛИ, НЕ и И.x % 2n == x < 0 ? x | ~(2n - 1) : x & (2n - 1)

Существуют также оптимизации для общих операций с постоянным модулем, в которых сначала вычисляется деление с использованием оптимизации с постоянным делителем .

Свойства (идентичности)

Некоторые операции по модулю могут быть факторизованы или расширены аналогично другим математическим операциям. Это может быть полезно в криптографических доказательствах, таких как обмен ключами Диффи–Хеллмана . Свойства, включающие умножение, деление и возведение в степень, обычно требуют, чтобы a и n были целыми числами.

• Личность:
  • ( а мод n ) мод n = а мод n .
  • n ^x mod n = 0 для всех положительных целых значений x .
  • Если p — простое число , не являющееся делителем b , то ab p ⁻¹ mod p = a mod ^p , согласно малой теореме Ферма .
• Обратное:
  • [(− a mod n ) + ( a mod n )] mod n знак равно 0 .
  • b ⁻¹ mod n обозначает модульную мультипликативную обратную величину , которая определена тогда и только тогда, когда b и n являются взаимно простыми числами , что имеет место, когда левая часть определена: [( b ⁻¹ mod n )( b mod n )] mod n = 1 .
• Распределительный:
  • ( a + b ) mod n = [( a mod n ) + ( b mod n )] mod n .
  • ab mod n = [( a mod n )( b mod n )] mod n .
• Раздел (определение): ⁠а/б⁠ mod n = [( a mod n )( b ⁻¹ mod n )] mod n , когда правая часть определена (то есть когда b и n взаимно просты ), и не определена в противном случае.
• Обратное умножение: [( ab mod n )( b ⁻¹ mod n )] mod n = a mod n .

В языках программирования

Кроме того, многие компьютерные системы предоставляют divmodфункционал, который производит частное и остаток одновременно. Примерами служат инструкция архитектуры x86IDIV , функция языка программирования C div()и функция Pythondivmod() .

Обобщения

Модуль со смещением

Иногда полезно, чтобы результат деления по модулю n лежал не между 0 и n − 1 , а между некоторым числом d и d + n − 1. В этом случае d называется смещением , а d = 1 встречается особенно часто.

Похоже, что для этой операции не существует стандартной нотации, поэтому давайте предварительно будем использовать a mod _d n . Таким образом, у нас есть следующее определение: ^[57] x = a mod _d n на всякий случай d ≤ x ≤ d + n − 1 и x mod n = a mod n . Очевидно, что обычная операция по модулю соответствует нулевому смещению: a mod n = a mod ₀ n .

Операция по модулю со смещением связана с функцией пола следующим образом:

${\displaystyle a\operatorname {mod} _{d}n=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor .}$

Чтобы увидеть это, пусть . Сначала покажем, что x mod n = a mod n . В общем случае верно, что ( a + bn ) mod n = a mod n для всех целых чисел b ; таким образом, это верно и в частном случае, когда ; но это означает, что , что мы и хотели доказать. Осталось показать, что d ≤ x ≤ d + n − 1 . Пусть k и r — целые числа, такие что a − d = kn + r с 0 ≤ r ≤ n − 1 (см. Евклидово деление ). Тогда , таким образом . Теперь возьмем 0 ≤ r ≤ n − 1 и прибавим d к обеим сторонам, получив d ≤ d + r ≤ d + n − 1 . Но мы видели, что x = d + r , так что мы закончили. ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ ${\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}$ ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$

Модуль со смещением a mod _d n реализован в Mathematica как Mod[a, n, d] . ^[57]

Реализация других определений по модулю с использованием усечения

Несмотря на математическую элегантность деления Кнута и евклидова деления, в языках программирования обычно гораздо чаще встречается усеченное деление по модулю. Лейен предоставляет следующие алгоритмы для вычисления двух делений, заданных усеченным целочисленным делением: ^[5]

/* Евклидов и Floored divmod, в стиле ldiv() языка C */ typedef struct { /* Эта структура является частью C stdlib.h, но воспроизведена здесь для ясности */ long int quot ; long int rem ; } ldiv_t ;          /* Евклидово деление */ inline ldiv_t ldivE ( long numer , long denom ) { /* Языки C99 и C++11 определяют оба эти метода как усечение. */ long q = numer / denom ; long r = numer % denom ; if ( r < 0 ) { if ( denom > 0 ) { q = q - 1 ; r = r + denom ; } else { q = q + 1 ; r = r - denom ; } } return ( ldiv_t ){. quot = q , . rem = r }; }                                                             /* Деление с меньшим числом */ inline ldiv_t ldivF ( long numer , long denom ) { long q = numer / denom ; long r = numer % denom ; if (( r > 0 && denom < 0 ) || ( r < 0 && denom > 0 )) { q = q - 1 ; r = r + denom ; } return ( ldiv_t ){. quot = q , . rem = r }; }                                                     

Для обоих случаев остаток можно вычислить независимо от частного, но не наоборот. Операции здесь объединены для экономии места на экране, поскольку логические ветви одинаковы.

Смотрите также

• Модуль (значение) – множество значений слова modulo , все из которых возникли после введения Карлом Ф. Гауссом модульной арифметики в 1801 году.
• Модуль (математика) , общее использование термина в математике
• Модульное возведение в степень
• Поворот (угол)

Примечания

1. Математически эти два варианта являются всего лишь двумя из бесконечного числа вариантов, доступных для неравенства, которому удовлетворяет остаток .
2. Порядок аргументов меняет местами, т.е. α|ωвычисляет остаток при делении на . ${\displaystyle \omega {\bmod {\alpha }}}$ωα
3. C99 и C++11 определяют поведение, которое %должно быть усечено. ^[9] Стандарты до этого момента оставляли поведение, определяемое реализацией. ^[10]
4. Делитель должен быть положительным, в противном случае не определен.
5. Как обсуждал Буте, определения ISO Pascal для divи modне подчиняются тождеству деления D = d · ( D / d ) + D  % d и, таким образом, в корне нарушены.
6. Perl обычно использует арифметический оператор по модулю, который не зависит от машины. Примеры и исключения см. в документации Perl по мультипликативным операторам. ^[43]

Ссылки

1. Weisstein, Eric W. "Конгруэнтность". Wolfram MathWorld . Получено 27.08.2020 .
2. Колдуэлл, Крис. "остаток". Prime Glossary . Получено 27 августа 2020 г.
3. Кнут, Дональд Э. (1972). Искусство программирования . Эддисон-Уэсли.
4. Boute, Raymond T. (апрель 1992 г.). «Евклидово определение функций div и mod». ACM Transactions on Programming Languages ​​and Systems . 14 (2). ACM Press (Нью-Йорк, штат Нью-Йорк, США): 127–144. doi :10.1145/128861.128862. hdl : 1854/LU-314490 . S2CID  8321674.
5. Leijen, Daan (3 декабря 2001 г.). «Деление и модуль для компьютерных ученых» (PDF) . Получено 25.12.2014 .
6. Peterson, Doctor (5 июля 2001 г.). "Mod Function and Negative Numbers". Math Forum - Ask Dr. Math . Архивировано из оригинала 2019-10-22 . Получено 22 октября 2019 г.
7. Хорват, Адам (5 июля 2012 г.). «Более быстрое деление и операция по модулю — сила двойки».
8. ISO/IEC 8652:2012 - Информационные технологии — Языки программирования — Ada . ISO , IEC . 2012. раздел 4.5.5 Операторы умножения.
9. "Спецификация C99 (ISO/IEC 9899:TC2)" (PDF) . 2005-05-06. раздел 6.5.5 Мультипликативные операторы . Получено 16 августа 2018 г. .
10. ISO/IEC 14882:2003: Языки программирования – C++ . Международная организация по стандартизации (ISO), Международная электротехническая комиссия (IEC). 2003. раздел 5.6.4. бинарный оператор % возвращает остаток от деления первого выражения на второе. .... Если оба операнда неотрицательны, то остаток неотрицателен; в противном случае знак остатка определяется реализацией.
11. ISO/IEC 9899:1990: Языки программирования – C. ISO , IEC . 1990. раздел 7.5.6.4. Функция fmod возвращает значение x - i * y для некоторого целого числа i, такого, что если y не равен нулю, результат имеет тот же знак, что и x , и величину, меньшую величины y .
12. dotnet-bot. "Math.IEEERemainder(Double, Double) Method (System)". Microsoft Learn . Получено 2022-10-04 .
13. "clojure.core - Документация API Clojure v1.10.3". clojure.github.io . Получено 2022-03-16 .
14. "clojure.core - Документация API Clojure v1.10.3". clojure.github.io . Получено 2022-03-16 .
15. ISO/IEC JTC 1/SC 22/WG 4 (январь 2023 г.). ISO/IEC 1989:2023 – Язык программирования COBOL . ISO .{{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )
16. Операторы CoffeeScript
17. ISO/IEC JTC 1/SC 22 (февраль 2012 г.). ISO/IEC 23271:2012 — Информационные технологии — Инфраструктура общего языка (CLI). ISO . §§ III.3.55–56.{{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка )
18. "Выражения - Язык программирования D". dlang.org . Получено 01.06.2021 .
19. "operator % method - num class - dart:core library - Dart API". api.dart.dev . Получено 2021-06-01 .
20. "remainder method - num class - dart:core library - Dart API". api.dart.dev . Получено 2021-06-01 .
21. "Ядро — Elixir v1.11.3". hexdocs.pm . Получено 2021-01-28 .
22. "Integer — Elixir v1.11.3". hexdocs.pm . Получено 2021-01-28 .
23. "Basics - core 1.0.5". package.elm-lang.org . Получено 2022-03-16 .
24. "Basics - core 1.0.5". package.elm-lang.org . Получено 2022-03-16 .
25. "Erlang -- math". erlang.org . Получено 2021-06-01 .
26. ANSI (28 января 1987 г.). Языки программирования — Полный BASIC. Нью-Йорк: Американский национальный институт стандартов. § 5.4.4. X по модулю Y, т. е. XY*INT(X/Y).
27. ANSI (28 января 1987 г.). Языки программирования — Полный BASIC. Нью-Йорк: Американский национальный институт стандартов. § 5.4.4. Функция остатка, т. е. XY*IP(X/Y).
28. "GLSL Language Specification, Version 4.50.7" (PDF) . раздел 5.9 Выражения. Если оба операнда неотрицательны, то остаток неотрицателен. Результаты не определены, если один или оба операнда отрицательны.
29. «Спецификация языка GLSL, версия 4.50.7» (PDF) . раздел 8.3 Общие функции.
30. "Спецификация языка программирования Go - Язык программирования Go". go.dev . Получено 28.02.2022 .
31. "math package - math - pkg.go.dev". pkg.go.dev . Получено 28.02.2022 .
32. "большой пакет - math/big - pkg.go.dev". pkg.go.dev . Получено 28.02.2022 .
33. "большой пакет - math/big - pkg.go.dev". pkg.go.dev . Получено 2024-04-12 .
34. "6 предопределенных типов и классов". www.haskell.org . Получено 2022-05-22 .
35. "Операторы". Microsoft . Получено 2021-07-19 . Оператор % определен только в случаях, когда обе стороны положительны или обе стороны отрицательны. В отличие от C, он также работает с типами данных с плавающей точкой, а также с целыми числами.
36. "Математика · Язык Julia". docs.julialang.org . Получено 20.11.2021 .
37. "Математика · Язык Julia". docs.julialang.org . Получено 20.11.2021 .
38. "rem - Язык программирования Kotlin". Kotlin . Получено 2021-05-05 .
39. "mod - Язык программирования Kotlin". Kotlin . Получено 2021-05-05 .
40. "Глава 3: Язык NASM". NASM - Netwide Assembler версии 2.15.05 .
41. "Библиотека OCaml: Stdlib". ocaml.org . Получено 2022-02-19 .
42. "Библиотека OCaml: Stdlib". ocaml.org . Получено 2022-02-19 .
43. Документация Perl
44. "PHP: Арифметические операторы - Руководство". www.php.net . Получено 20.11.2021 .
45. "PHP: fmod - Руководство". www.php.net . Получено 2021-11-20 .
46. "Евклидово кольцо".
47. QuantumWriter. "Выражения". docs.microsoft.com . Получено 11 июля 2018 г. .
48. "R: Арифметические операторы". search.r-project.org . Получено 2022-12-24 .
49. "F32 - Ржавчина".
50. r6rs.org
51. "Shell Command Language". pubs.opengroup.org . Получено 2021-02-05 .
52. "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
53. "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
54. "Документация для разработчиков Apple". developer.apple.com . Получено 20.11.2021 .
55. Rossberg, Andreas, ed. (19 апреля 2022 г.). «Спецификация ядра WebAssembly: версия 2.0». Консорциум World Wide Web . § 4.3.2 Целочисленные операции.
56. "Документация Zig". Язык программирования Zig . Получено 2022-12-18 .
57. "Mod". Wolfram Language & System Documentation Center . Wolfram Research . 2020. Получено 8 апреля 2020 г.

Внешние ссылки

• Различные виды целочисленного деления
• Modulorama, анимация циклического представления таблиц умножения (объяснение на французском)