В формальной теории языка контекстно-свободная грамматика ( CFG ) — это формальная грамматика , правила производства которой могут быть применены к нетерминальному символу независимо от его контекста. В частности, в контекстно-свободной грамматике каждое правило производства имеет вид
с одним нетерминальным символом и строкой терминалов и/или нетерминалов ( может быть пустым). Независимо от того, какие символы его окружают, один нетерминал слева всегда можно заменить на справа . Это отличает его от контекстно-зависимой грамматики , которая может иметь правила производства в форме с нетерминальным символом и , , и строками терминалов и/или нетерминальных символов.
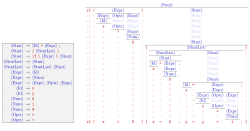
Формальная грамматика по сути является набором правил производства, которые описывают все возможные строки в данном формальном языке. Правила производства являются простыми заменами. Например, первое правило на рисунке,
заменяет на . Для данного нетерминального символа может быть несколько правил замены. Язык, генерируемый грамматикой, представляет собой набор всех строк терминальных символов, которые могут быть получены путем повторного применения правил из некоторого конкретного нетерминального символа («начальный символ»). Нетерминальные символы используются в процессе вывода, но не появляются в его конечной строке результата.
Языки, генерируемые контекстно-свободными грамматиками, известны как контекстно-свободные языки (CFL). Различные контекстно-свободные грамматики могут генерировать один и тот же контекстно-свободный язык. Важно различать свойства языка (внутренние свойства) от свойств конкретной грамматики (внешние свойства). Вопрос о равенстве языков (генерируют ли две заданные контекстно-свободные грамматики один и тот же язык?) неразрешим .
Контекстно-свободные грамматики возникают в лингвистике , где они используются для описания структуры предложений и слов на естественном языке , и они были изобретены лингвистом Ноамом Хомским для этой цели. Напротив, в компьютерной науке , по мере увеличения использования рекурсивно определенных концепций, они использовались все больше и больше. В раннем приложении грамматики использовались для описания структуры языков программирования . В более новом приложении они используются в существенной части расширяемого языка разметки (XML), называемой определением типа документа . [2]
В лингвистике некоторые авторы используют термин грамматика фразовой структуры для обозначения контекстно-свободных грамматик, в то время как грамматики фразовой структуры отличаются от грамматик зависимостей . В информатике популярной нотацией для контекстно-свободных грамматик является форма Бэкуса–Наура , или БНФ.
По крайней мере со времен древнеиндийского ученого Панини лингвисты описывали грамматики языков с точки зрения их блочной структуры и описывали, как предложения рекурсивно строятся из более мелких фраз и, в конечном счете, отдельных слов или элементов слов. Существенным свойством этих блочных структур является то, что логические единицы никогда не перекрываются. Например, предложение:
можно логически заключить в скобки (с помощью логических метасимволов [ ] ) следующим образом:
Контекстно-свободная грамматика предоставляет простой и математически точный механизм для описания методов, с помощью которых фразы в некотором естественном языке строятся из более мелких блоков, естественным образом фиксируя «блочную структуру» предложений. Его простота делает формализм поддающимся строгому математическому изучению. Важные особенности синтаксиса естественного языка, такие как согласование и ссылка, не являются частью контекстно-свободной грамматики, но базовая рекурсивная структура предложений, способ, которым предложения вкладывают друг в друга, и способ, которым списки прилагательных и наречий поглощаются существительными и глаголами, описаны точно.
Контекстно-свободные грамматики представляют собой особую форму систем Semi-Thue , которые в своей общей форме восходят к работам Акселя Туэ .
Формализм контекстно-свободных грамматик был разработан в середине 1950-х годов Ноамом Хомским [3] , а также их классификация как особого типа формальной грамматики (которую он назвал грамматиками фразовой структуры ). [4] Некоторые авторы, однако, резервируют этот термин для более ограниченных грамматик в иерархии Хомского: контекстно-зависимые грамматики или контекстно-свободные грамматики. В более широком смысле грамматики фразовой структуры также известны как грамматики составляющих. Определяющей чертой грамматик фразовой структуры является, таким образом, их приверженность отношению составляющих, в отличие от отношения зависимости грамматик зависимости . В структуре генеративной грамматики Хомского синтаксис естественного языка описывался контекстно-свободными правилами в сочетании с правилами преобразования. [5]
Блочная структура была введена в языки программирования проектом Algol (1957–1960), который, как следствие, также включал контекстно-свободную грамматику [6] для описания результирующего синтаксиса Algol. Это стало стандартной особенностью компьютерных языков, а нотация для грамматик, используемых в конкретных описаниях компьютерных языков, стала известна как форма Бэкуса–Наура , в честь двух членов комитета по проектированию языка Algol. [3] Аспект «блочной структуры», который охватывают контекстно-свободные грамматики, настолько фундаментален для грамматики, что термины синтаксис и грамматика часто отождествляются с правилами контекстно-свободной грамматики, особенно в информатике. Формальные ограничения, не охватываемые грамматикой, затем считаются частью «семантики» языка.
Контекстно-свободные грамматики достаточно просты, чтобы позволить строить эффективные алгоритмы синтаксического анализа , которые для заданной строки определяют, может ли она быть сгенерирована из грамматики и как. Примером такого алгоритма является парсер Эрли , в то время как широко используемые парсеры LR и LL являются более простыми алгоритмами, которые имеют дело только с более ограничивающими подмножествами контекстно-свободных грамматик.
Контекстно-свободная грамматика G определяется 4-кортежем , где [7]
Правило продуцирования в R математически формализуется как пара , где — нетерминал, а — строка переменных и/или терминалов; вместо использования упорядоченной парной нотации правила продуцирования обычно записываются с использованием оператора стрелки, в левой части которого находится , а в правой — β : .
Допускается, чтобы β была пустой строкой , и в этом случае принято обозначать ее как ε. Форма называется ε -производством. [8]
Обычно все правые стороны для одной и той же левой стороны перечисляются на одной строке, используя | ( вертикальную черту ) для их разделения. Правила и, следовательно, могут быть записаны как . В этом случае и называются первой и второй альтернативой соответственно.
Для любых строк мы говорим, что u напрямую даёт v , что записывается как , если с и такими, что и . Таким образом, v является результатом применения правила к u .
Для любых строк мы говорим, что u дает v или v выводится из u , если существует положительное целое число k и строки такие, что . Это отношение обозначается , или в некоторых учебниках. Если , отношение выполняется. Другими словами, и являются рефлексивным транзитивным замыканием (позволяющим строке дать себя) и транзитивным замыканием (требующим по крайней мере одного шага) , соответственно.
Язык грамматики – это набор
всех строк терминальных символов, выводимых из начального символа.
Язык L называется контекстно-свободным языком (CFL), если существует CFG G , такой что .
Недетерминированные магазинные автоматы распознают именно контекстно-свободные языки.
Грамматика с постановками
является контекстно-свободным. Это не является правильным, так как включает ε-производство. Типичный вывод в этой грамматике:
Это ясно показывает, что . Язык является контекстно-свободным, однако можно доказать, что он не является регулярным .
Если постановки
добавляются, получается контекстно-свободная грамматика для множества всех палиндромов в алфавите { a , b } . [9]
Каноническим примером контекстно-свободной грамматики является сопоставление скобок, которое является репрезентативным для общего случая. Имеется два терминальных символа "(" и ")" и один нетерминальный символ S. Правила производства таковы:
Первое правило позволяет символу S умножаться; второе правило позволяет заключать символ S в соответствующие скобки; а третье правило завершает рекурсию. [10]
Вторым каноническим примером являются два различных вида соответствующих вложенных скобок, описываемых следующими конструкциями:
с терминальными символами [ ] ( ) и нетерминальным S.
В этой грамматике можно вывести следующую последовательность:
В контекстно-свободной грамматике мы можем объединять символы в пары так, как мы это делаем с помощью скобок . Самый простой пример:
Эта грамматика порождает язык , который не является регулярным (согласно лемме о накачке для регулярных языков ).
Специальный символ ε обозначает пустую строку. Изменив приведенную выше грамматику на
мы получаем грамматику, генерирующую язык вместо этого. Она отличается только тем, что содержит пустую строку, тогда как исходная грамматика ее не содержала.
Контекстно-свободная грамматика для языка, состоящего из всех строк над {a,b}, содержащих неравное количество букв a и b:
Здесь нетерминал T может генерировать все строки с большим количеством a, чем b, нетерминал U генерирует все строки с большим количеством b, чем a, а нетерминал V генерирует все строки с равным количеством a и b. Исключение третьей альтернативы в правилах для T и U не ограничивает язык грамматики.
Другим примером нерегулярного языка является . Он является контекстно-свободным, поскольку может быть сгенерирован следующей контекстно-свободной грамматикой:
Правила образования терминов и формул формальной логики соответствуют определению контекстно-свободной грамматики, за исключением того, что набор символов может быть бесконечным и может быть более одного начального символа.
В отличие от правильно сформированных вложенных скобок и квадратных скобок в предыдущем разделе, не существует контекстно-свободной грамматики для генерации всех последовательностей двух различных типов скобок, каждая из которых сбалансирована отдельно, игнорируя другую , где два типа не должны вкладываться друг в друга, например:
или
Тот факт, что этот язык не является контекстно-свободным, можно доказать с помощью леммы о накачке для контекстно-свободных языков и доказательства от противного, заметив, что все слова формы должны принадлежать языку. Этот язык вместо этого принадлежит к более общему классу и может быть описан конъюнктивной грамматикой , которая в свою очередь также включает другие неконтекстно-свободные языки, такие как язык всех слов формы .
Каждая регулярная грамматика является контекстно-свободной, но не все контекстно-свободные грамматики являются регулярными. [11] Например, следующая контекстно-свободная грамматика также является регулярной.
Терминалами здесь являются a и b , а единственным нетерминалом является S. Описанный язык — это все непустые строки s и s, которые заканчиваются на .
Эта грамматика является регулярной : ни одно правило не имеет более одного нетерминала в правой части, и каждый из этих нетерминалов находится на одном и том же конце правой части.
Каждая регулярная грамматика напрямую соответствует недетерминированному конечному автомату , поэтому мы знаем, что это регулярный язык .
Используя вертикальные черты, грамматику выше можно описать более кратко следующим образом:
Вывод строки для грамматики — это последовательность применений правил грамматики , которые преобразуют начальный символ в строку. Вывод доказывает, что строка принадлежит языку грамматики.
Вывод полностью определяется путем указания для каждого шага:
Для ясности обычно приводится также промежуточная строка.
Например, с грамматикой:
строка
может быть получен из начального символа S с помощью следующего вывода:
Часто применяется стратегия, которая детерминированно выбирает следующий нетерминал для переписывания:
При такой стратегии вывод полностью определяется последовательностью применяемых правил. Например, один левый вывод той же строки —
что можно резюмировать как
Один из самых правых выводов:
что можно резюмировать как
Различие между левосторонним выводом и правосторонним выводом важно, поскольку в большинстве парсеров преобразование входных данных определяется путем предоставления фрагмента кода для каждого правила грамматики, который выполняется всякий раз, когда правило применяется. Поэтому важно знать, определяет ли парсер левостороннее или правостороннее вывод, поскольку это определяет порядок, в котором будут выполняться фрагменты кода. См. пример LL-парсеров и LR-парсеров .
Вывод также в некотором смысле накладывает иерархическую структуру на строку, которая выводится. Например, если строка "1 + 1 + a" выводится в соответствии с самым левым выводом, описанным выше, структура строки будет следующей:
где {...} S указывает на подстроку, распознаваемую как принадлежащую S. Эту иерархию также можно рассматривать как дерево:
Это дерево называется деревом разбора или «конкретным синтаксическим деревом» строки, в отличие от абстрактного синтаксического дерева . В этом случае представленные левое и правое производные определяют одно и то же дерево разбора; однако, существует другое правое производное той же строки
который определяет строку с другой структурой
и другое дерево разбора:
Однако следует отметить, что оба дерева разбора могут быть получены как с помощью самого левого, так и самого правого вывода. Например, последнее дерево может быть получено с помощью самого левого вывода следующим образом:
Если строка в языке грамматики имеет более одного дерева разбора, то грамматика называется неоднозначной грамматикой . Такие грамматики обычно трудно анализировать, потому что анализатор не всегда может решить, какое правило грамматики он должен применить. Обычно неоднозначность является особенностью грамматики, а не языка, и можно найти однозначную грамматику, которая генерирует тот же контекстно-свободный язык. Однако существуют определенные языки, которые могут быть сгенерированы только неоднозначными грамматиками; такие языки называются изначально неоднозначными языками .
Каждая контекстно-свободная грамматика без ε-производства имеет эквивалентную грамматику в нормальной форме Хомского и грамматику в нормальной форме Грейбаха . «Эквивалентный» здесь означает, что две грамматики генерируют один и тот же язык.
Особенно простая форма правил производства в грамматиках нормальной формы Хомского имеет как теоретические, так и практические последствия. Например, при наличии контекстно-свободной грамматики можно использовать нормальную форму Хомского для построения полиномиального алгоритма, который решает, находится ли данная строка в языке, представленном этой грамматикой, или нет ( алгоритм CYK ).
Контекстно-свободные языки замкнуты относительно различных операций, то есть, если языки K и L являются контекстно-свободными, то таковым является и результат следующих операций:
Они не замкнуты относительно общего пересечения (следовательно, и относительно дополнения ) и разности множеств. [16]
Ниже приведены некоторые разрешимые проблемы, связанные с контекстно-свободными грамматиками.
Задача синтаксического анализа, проверяющая, принадлежит ли данное слово языку, заданному контекстно-свободной грамматикой, разрешима с помощью одного из универсальных алгоритмов синтаксического анализа:
Контекстно-свободный синтаксический анализ для грамматик нормальной формы Хомского был показан Лесли Г. Валиантом как сводимый к умножению булевых матриц , таким образом наследуя его верхнюю границу сложности O ( n 2,3728639 ). [17] [18] [примечание 1] Наоборот, Лиллиан Ли показала, что O ( n 3−ε ) умножение булевых матриц сводимо к O ( n 3−3ε ) синтаксическому анализу CFG, таким образом установив своего рода нижнюю границу для последнего. [19]
Нетерминальный символ называется продуктивным , или порождающим , если существует вывод для некоторой строки терминальных символов. называется достижимым , если из начального символа существует вывод для некоторых строк нетерминальных и терминальных символов. называется бесполезным, если он недостижим или непродуктивен. называется обнуляемым, если существует вывод . Правило называется ε-производством . Вывод называется циклом .
Известно, что алгоритмы исключают из заданной грамматики, не изменяя ее сгенерированный язык,
В частности, альтернатива, содержащая бесполезный нетерминальный символ, может быть удалена из правой части правила. Такие правила и альтернативы называются бесполезными . [25]
В представленном примере грамматики нетерминал D недостижим, а E непродуктивен, тогда как C → C приводит к циклу. Следовательно, исключение последних трех правил не меняет язык, сгенерированный грамматикой, как и исключение альтернатив "| Cc | Ee " из правой части правила для S .
Говорят, что контекстно-свободная грамматика является правильной, если она не содержит ни бесполезных символов, ни ε-порождений, ни циклов. [26] Объединяя вышеприведенные алгоритмы, каждую контекстно-свободную грамматику, не порождающую ε, можно преобразовать в слабо эквивалентную правильную.
Можно решить, является ли данная грамматика регулярной грамматикой , [27] а также является ли она грамматикой LL( k ) для данного k ≥0. [28] : 233 Если k не задано, последняя проблема неразрешима. [28] : 252
Для контекстно-свободной грамматики невозможно решить, является ли ее язык регулярным [29] или является ли он языком LL( k ) для заданного k . [28] : 254
Существуют алгоритмы, позволяющие определить, является ли язык данной контекстно-свободной грамматики пустым, а также является ли он конечным. [30]
Некоторые вопросы, неразрешимые для более широких классов грамматик, становятся разрешимыми для контекстно-свободных грамматик; например, проблема пустоты (генерирует ли грамматика вообще какие-либо терминальные строки) неразрешима для контекстно-зависимых грамматик , но разрешима для контекстно-свободных грамматик.
Однако многие проблемы неразрешимы даже для контекстно-свободных грамматик; наиболее важные из них рассматриваются ниже.
Учитывая CFG, генерирует ли он язык всех строк в алфавите терминальных символов, используемых в его правилах? [31] [32]
Сведение к этой проблеме можно продемонстрировать на основе известной неразрешимой проблемы определения того, принимает ли машина Тьюринга конкретный вход ( проблема остановки ). Сведение использует концепцию истории вычислений , строки, описывающей все вычисления машины Тьюринга . Можно построить CFG, который генерирует все строки, не принимающие истории вычислений для конкретной машины Тьюринга на конкретном входе, и, таким образом, он будет принимать все строки, только если машина не принимает этот вход.
Учитывая два CFG, генерируют ли они один и тот же язык? [32] [33]
Неразрешимость этой проблемы является прямым следствием предыдущей: невозможно даже решить, эквивалентна ли CFG тривиальной CFG, определяющей язык всех строк.
Учитывая два CFG, может ли первый из них сгенерировать все строки, которые может сгенерировать второй? [32] [33]
Если бы эта проблема была разрешима, то можно было бы решить и вопрос о равенстве языков: два CFG и генерируют один и тот же язык, если является подмножеством и является подмножеством .
Используя теорему Грейбаха , можно показать, что две следующие проблемы неразрешимы:
Если задан CFG, является ли он неоднозначным ?
Неразрешимость этой проблемы следует из того факта, что если бы существовал алгоритм определения неоднозначности, то можно было бы решить проблему соответствий Поста , которая, как известно, неразрешима. [34] Это можно доказать с помощью леммы Огдена . [35]
Имея две грамматики CFG, можно ли вывести какую-либо строку из обеих грамматик?
Если бы эта проблема была разрешима, неразрешимая проблема почтовой корреспонденции (PCP) также могла бы быть решена: даны строки в некотором алфавите , пусть грамматика состоит из правила
где обозначает перевернутую строку и не встречается среди ; и пусть грамматика состоит из правила
Тогда экземпляр PCP, заданный как , имеет решение тогда и только тогда, когда и разделяют выводимую строку. Левая часть строки (до ) будет представлять верхнюю часть решения для экземпляра PCP, тогда как правая сторона будет нижней частью в обратном порядке.
Очевидный способ расширить формализм контекстно-свободной грамматики — разрешить нетерминалам иметь аргументы, значения которых передаются в рамках правил. Это позволяет естественным образом выражать такие особенности языка, как согласование и ссылка , и аналоги языка программирования, такие как правильное использование и определение идентификаторов. Например, теперь мы можем легко выразить, что в английских предложениях подлежащее и глагол должны согласовываться в числе. В информатике примерами такого подхода являются аффиксные грамматики , атрибутные грамматики , индексированные грамматики и двухуровневые грамматики Ван Вейнгаардена . Аналогичные расширения существуют в лингвистике.
Расширенная контекстно-свободная грамматика (или регулярная правая часть грамматики ) — это та, в которой правая часть правил производства может быть регулярным выражением над терминалами и нетерминалами грамматики. Расширенные контекстно-свободные грамматики описывают именно контекстно-свободные языки. [36]
Другое расширение — разрешить дополнительным терминальным символам появляться в левой части правил, ограничивая их применение. Это создает формализм контекстно-зависимых грамматик .
Существует ряд важных подклассов контекстно-свободных грамматик:
LR-разбор расширяет LL-разбор для поддержки большего диапазона грамматик; в свою очередь, обобщенный LR-разбор расширяет LR-разбор для поддержки произвольных контекстно-свободных грамматик. На LL-грамматиках и LR-грамматиках он по сути выполняет LL-разбор и LR-разбор соответственно, тогда как на недетерминированных грамматиках он настолько эффективен, насколько можно ожидать. Хотя GLR-разбор был разработан в 1980-х годах, многие новые определения языков и генераторы синтаксических анализаторов продолжают основываться на LL-, LALR- или LR-разборе вплоть до настоящего времени.
Первоначально Хомский надеялся преодолеть ограничения контекстно-свободных грамматик, добавив правила преобразования . [4]
Такие правила являются еще одним стандартным приемом в традиционной лингвистике; например, пассивация в английском языке. Большая часть генеративной грамматики была посвящена поиску способов совершенствования описательных механизмов грамматики фразовой структуры и правил трансформации, чтобы можно было выразить именно те типы вещей, которые на самом деле позволяет естественный язык. Разрешение произвольных трансформаций не соответствует этой цели: они слишком сильны, будучи полными по Тьюрингу , если не добавлены существенные ограничения (например, никаких трансформаций, которые вводят и затем переписывают символы в контекстно-свободной манере).
Общая позиция Хомского относительно неконтекстной независимости естественного языка сохранилась с тех пор [37], хотя его конкретные примеры, касающиеся неадекватности контекстно-свободных грамматик с точки зрения их слабой генеративной способности, были позже опровергнуты. [38] Джеральд Газдар и Джеффри Пуллум утверждали, что, несмотря на несколько неконтекстно-свободных конструкций в естественном языке (таких как кросс-сериальные зависимости в швейцарском немецком [37] и редупликация в бамбара [39] ), подавляющее большинство форм в естественном языке действительно являются контекстно-свободными. [38]
Каждая конструкция, которая может быть описана регулярным выражением, может быть описана [контекстно-свободной] грамматикой, но не наоборот.