Невязкий поток

Течение жидкостей с нулевой вязкостью (сверхтекучих жидкостей)

В гидродинамике невязкий поток — это поток невязкой жидкости , которая имеет нулевую вязкость . ^[1]

Число Рейнольдса невязкого течения стремится к бесконечности, когда вязкость стремится к нулю. Когда вязкие силы пренебрегаются, как в случае невязкого течения, уравнение Навье–Стокса можно упростить до формы, известной как уравнение Эйлера . Это упрощенное уравнение применимо к невязкому течению, а также к течению с низкой вязкостью и числом Рейнольдса, намного большим единицы. Используя уравнение Эйлера, многие задачи динамики жидкости, связанные с низкой вязкостью, легко решаются, однако предполагаемая пренебрежимо малая вязкость больше не справедлива в области жидкости вблизи твердой границы (пограничный слой ) или, в более общем смысле, в областях с большими градиентами скорости , которые, очевидно, сопровождаются вязкими силами. ^{[1] [2] [3]}

Течение сверхтекучей жидкости является невязким. ^[4]

Невязкие течения в целом подразделяются на потенциальные течения (или безвихревые течения) и вращательные невязкие течения.

гипотеза Прандтля

На этих диаграммах показаны разделительные линии тока, связанные с аэродинамическим профилем в двумерном невязком потоке.
Верхняя диаграмма показывает нулевую циркуляцию и нулевую подъемную силу. Она подразумевает высокоскоростной вихревой поток на задней кромке, что, как известно, неточно в модели стационарного состояния.
Нижняя диаграмма показывает условие Кутты, которое подразумевает конечную циркуляцию, конечную подъемную силу и отсутствие вихревого потока на задней кромке. Известно, что эти характеристики точны как модели стационарного состояния в реальной жидкости.

Людвиг Прандтль разработал современную концепцию пограничного слоя . Его гипотеза устанавливает, что для жидкостей с низкой вязкостью сдвиговые силы, обусловленные вязкостью, проявляются только в тонких областях на границе жидкости, прилегающих к твердым поверхностям. За пределами этих областей и в областях благоприятного градиента давления вязкие сдвиговые силы отсутствуют, поэтому поле течения жидкости можно считать таким же, как и течение невязкой жидкости. Используя гипотезу Прандтля, можно оценить течение реальной жидкости в областях благоприятного градиента давления, предполагая невязкое течение и исследуя безвихревую картину течения вокруг твердого тела. ^[5]

Реальные жидкости испытывают разделение пограничного слоя и возникающие турбулентные следы, но эти явления не могут быть смоделированы с использованием невязкого течения. Разделение пограничного слоя обычно происходит там, где градиент давления меняет знак с благоприятного на неблагоприятный, поэтому неточно использовать невязкое течение для оценки потока реальной жидкости в областях неблагоприятного градиента давления . ^[5]

Число Рейнольдса

Число Рейнольдса (Re) — безразмерная величина , которая обычно используется в гидродинамике и машиностроении. ^{[6] [7]} Первоначально описанное Джорджем Габриэлем Стоксом в 1850 году, оно стало популяризировано Осборном Рейнольдсом, в честь которого это понятие было названо Арнольдом Зоммерфельдом в 1908 году. ^{[7] [8] [9]} Число Рейнольдса рассчитывается как:

${\displaystyle Re={l_{c}v\rho \over \mu }}$

Значение представляет собой отношение инерционных сил к вязким силам в жидкости и полезно для определения относительной важности вязкости. ^[6] В невязком потоке, поскольку вязкие силы равны нулю, число Рейнольдса стремится к бесконечности. ^[1] Когда вязкие силы пренебрежимо малы, число Рейнольдса намного больше единицы. ^[1] В таких случаях (Re>>1) предположение о невязком потоке может быть полезным для упрощения многих задач динамики жидкости.

Уравнения Эйлера

Невязкое обтекание крыла, предполагающее циркуляцию , которая удовлетворяет условию Кутта

В публикации 1757 года Леонард Эйлер описал систему уравнений, управляющих невязким потоком: ^[10]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\rho \mathbf {g} }$

Предположение о невязком течении позволяет применять уравнение Эйлера к течениям, в которых вязкие силы незначительны. ^[1] Некоторые примеры включают обтекание крыла самолета, обтекание опор моста в реке и океанские течения. ^[1]

Уравнения Навье-Стокса

В 1845 году Джордж Габриэль Стокс опубликовал еще один важный набор уравнений, сегодня известный как уравнения Навье-Стокса . ^{[1] [11]} Клод-Луи Навье впервые разработал уравнения, используя молекулярную теорию, которая была впоследствии подтверждена Стоксом с помощью теории сплошной среды. ^[1] Уравнения Навье-Стокса описывают движение жидкостей: ^[1]

${\displaystyle \rho {D\mathbf {v} \over Dt}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g} }$

Когда жидкость невязкая или вязкость можно считать пренебрежимо малой, уравнение Навье-Стокса упрощается до уравнения Эйлера: ^[1] Это упрощение гораздо проще решить, и его можно применять ко многим типам течения, в которых вязкость пренебрежимо мала. ^[1] Некоторые примеры включают поток вокруг крыла самолета, поток вверх по течению вокруг опор моста в реке и океанские течения. ^[1]

Уравнение Навье-Стокса сводится к уравнению Эйлера, когда . Другое условие, которое приводит к устранению вязкой силы, это , и это приводит к «невязкому течению». ^[12] Такие течения оказываются вихреобразными. ${\displaystyle \mu =0}$ ${\displaystyle \nabla ^{2}\mathbf {v} =0}$

Течение, развивающееся над твердой поверхностью

Твердые границы

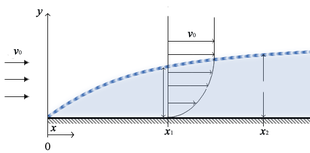
Важно отметить, что пренебрежимо малая вязкость больше не может предполагаться вблизи твердых границ, таких как в случае крыла самолета. ^[1] В турбулентных режимах течения (Re >> 1) вязкостью обычно можно пренебречь, однако это справедливо только на расстояниях, далеких от твердых границ раздела. ^[1] При рассмотрении течения вблизи твердой поверхности, такого как течение через трубу или вокруг крыла, удобно выделить четыре отдельные области течения вблизи поверхности: ^[1]

• Основной турбулентный поток: дальше всего от поверхности, вязкостью можно пренебречь.
• Инерционный подслой: Начало основного турбулентного потока, вязкость имеет лишь второстепенное значение.
• Буферный слой: преобразование между инерционным и вязким слоями.
• Вязкий подслой : Расположен ближе всего к поверхности, здесь важна вязкость.

Хотя эти различия могут быть полезным инструментом для иллюстрации значимости вязких сил вблизи твердых границ раздела, важно отметить, что эти области довольно условны. ^[1] Предполагая, что невязкий поток может быть полезным инструментом для решения многих задач динамики жидкости, однако это предположение требует тщательного рассмотрения подслоев жидкости, когда речь идет о твердых границах.

Сверхтекучие жидкости

Сверхтекучий гелий

Сверхтекучесть — это состояние вещества, при котором наблюдается течение без трения, нулевая вязкость, также известное как невязкое течение. ^[4]

На сегодняшний день гелий является единственной обнаруженной жидкостью, демонстрирующей сверхтекучесть. Гелий-4 становится сверхтекучим, как только он охлаждается до температуры ниже 2,2 К, известной как точка лямбда . ^[13] При температурах выше точки лямбда гелий существует как жидкость, демонстрирующая нормальное гидродинамическое поведение. Как только он охлаждается до температуры ниже 2,2 К, он начинает демонстрировать квантовое поведение. Например, в точке лямбда происходит резкое увеличение теплоемкости, по мере того как он продолжает охлаждаться, теплоемкость начинает уменьшаться с температурой. ^[14] Кроме того, теплопроводность очень велика, что способствует превосходным охлаждающим свойствам сверхтекучего гелия. ^[15] Аналогично обнаружено, что гелий-3 становится сверхтекучим при 2,491 мК.

Приложения

Спектрометры поддерживаются при очень низкой температуре, используя гелий в качестве охладителя. Это позволяет свести к минимуму фоновый поток в показаниях в дальнем инфракрасном диапазоне. Некоторые конструкции спектрометров могут быть простыми, но даже рама имеет самую высокую температуру менее 20 Кельвинов. Эти устройства нечасто используются, поскольку использовать сверхтекучий гелий по сравнению с другими охладителями очень дорого. ^[16]

Большой адронный коллайдер

Сверхтекучий гелий обладает очень высокой теплопроводностью, что делает его очень полезным для охлаждения сверхпроводников. Сверхпроводники, такие как те, что используются в LHC (Большом адронном коллайдере), охлаждаются до температур около 1,9 Кельвина. Эта температура позволяет ниобий-титановым магнитам достичь состояния сверхпроводника. Без использования сверхтекучего гелия эта температура была бы невозможна. Использование гелия для охлаждения до этих температур очень дорого, и охлаждающие системы, использующие альтернативные жидкости, более многочисленны. ^[17]

Другое применение сверхтекучего гелия — его использование в понимании квантовой механики. Использование лазеров для наблюдения за маленькими каплями позволяет ученым наблюдать поведение, которое обычно не может быть видимым. Это связано с тем, что весь гелий в каждой капле находится в одном и том же квантовом состоянии. Это применение само по себе не имеет практического применения, но оно помогает нам лучше понять квантовую механику, которая имеет свои собственные приложения.

Смотрите также

• Поток Куэтта
• Динамика жидкости
• Потенциальный поток , частный случай невязкого потока.
• Течение Стокса , в котором силы вязкости намного больше сил инерции.
• Вязкость

Ссылки

1. E., Стюарт, Уоррен; N., Лайтфут, Эдвин (2007-01-01). Явления переноса . Wiley. ISBN 9780470115398. OCLC  762715172.{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
2. Клэнси, Л.Дж., Аэродинамика , стр.xviii
3. Кунду, П.К., Коэн, И.М., и Ху, Х.Х., Механика жидкости , Глава 10, подраздел 1
4. S., Stringari (2016). Бозе-Эйнштейновская конденсация и сверхтекучесть . Oxford University Press. ISBN 9780198758884. OCLC  936040211.
5. Streeter, Victor L. (1966) Fluid Mechanics , разделы 5.6 и 7.1, 4-е издание, McGraw-Hill Book Co., Библиотека Конгресса, номер карточки каталога 66-15605
6. L., Bergman, Theodore; S., Lavine, Adrienne ; P., Incropera, Frank; P., Dewitt, David (2011-01-01). Основы тепло- и массопереноса . Wiley. ISBN 9780470501979. OCLC  875769912.{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
7. Rott, N (28.11.2003). «Заметка об истории числа Рейнольдса». Annual Review of Fluid Mechanics . 22 (1): 1–12. Bibcode : 1990AnRFM..22....1R. doi : 10.1146/annurev.fl.22.010190.000245.
8. Рейнольдс, Осборн (1883-01-01). «Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или извилистым, и закона сопротивления в параллельных каналах». Philosophical Transactions of the Royal Society of London . 174 : 935–982. Bibcode : 1883RSPT..174..935R. doi : 10.1098/rstl.1883.0029 . ISSN  0261-0523.
9. Стокс, ГГ (1851-01-01). «О влиянии внутреннего трения жидкостей на движение маятников». Труды Кембриджского философского общества . 9 : 8. Bibcode :1851TCaPS...9....8S.
10. Эйлер, Леонард (1757). «Принципы общих принципов состояния равновесия» [Общие принципы состояния равновесия]». Мемуары Берлинской академии наук . 11 : 217–273.
11. Стокс, ГГ (1845). «О теориях внутреннего трения движущихся жидкостей и равновесия и движения упругих твердых тел». Proc. Camb. Phil. Soc . 8 : 287–319.
12. Runstedtler, Allan (2013). «Невязкие потоки в гидродинамике». International Journal of Fluid Mechanics Research . 40 (2): 148–158. doi :10.1615/interjfluidmechres.v40.i2.50. ISSN  1064-2277.
13. «Этот месяц в истории физики». www.aps.org . Получено 2017-03-07 .
14. Ландау, Л. (1941). «Теория сверхтекучести гелия II». Physical Review . 60 (4): 356–358. Bibcode :1941PhRv...60..356L. doi :10.1103/physrev.60.356.
15. "Портал физики природы - оглядываясь назад - Двигаясь по течению - обнаружена сверхтекучесть". www.nature.com . Получено 07.03.2017 .
16. HOUCK, JR; WARD, DENNIS (1979-01-01). "Решётчатый спектрометр с жидким гелием для астрономических наблюдений в дальнем инфракрасном диапазоне". Publications of the Astronomical Society of the Pacific . 91 (539): 140–142. Bibcode : 1979PASP...91..140H. doi : 10.1086/130456 . JSTOR  40677459. S2CID  120273071.
17. "Криогеника: Низкие температуры, высокая производительность | CERN". home.cern . Получено 2017-02-14 .