В статистике нелинейная регрессия — это форма регрессионного анализа , в которой данные наблюдений моделируются функцией, которая представляет собой нелинейную комбинацию параметров модели и зависит от одной или нескольких независимых переменных. Данные аппроксимированы методом последовательных приближений.
В нелинейной регрессии статистическая модель вида
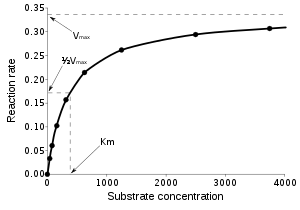
связывает вектор независимых переменных , и связанных с ним наблюдаемых зависимых переменных , . Функция нелинейна по компонентам вектора параметров , но в остальном произвольна. Например, модель Михаэлиса-Ментен для кинетики ферментов имеет два параметра и одну независимую переменную, связанные соотношением: [a]
Эта функция является нелинейной, поскольку ее нельзя выразить как линейную комбинацию двух s.
Систематическая ошибка может присутствовать в независимых переменных, но ее обработка выходит за рамки регрессионного анализа. Если независимые переменные не лишены ошибок, это модель ошибок в переменных , также выходящая за рамки этой области.
Другие примеры нелинейных функций включают экспоненциальные функции , логарифмические функции , тригонометрические функции , степенные функции , функцию Гаусса и распределения Лоренца . Некоторые функции, такие как показательная или логарифмическая функции, можно преобразовать так, чтобы они стали линейными. При таком преобразовании можно выполнить стандартную линейную регрессию, но ее следует применять с осторожностью. Для получения более подробной информации см. Линеаризация § Преобразование ниже.
В общем, не существует выражения в закрытой форме для наиболее подходящих параметров, как в линейной регрессии . Обычно алгоритмы численной оптимизации применяются для определения наиболее подходящих параметров. Опять же, в отличие от линейной регрессии, у оптимизируемой функции может быть много локальных минимумов , и даже глобальный минимум может давать смещенную оценку. На практике оценочные значения параметров используются вместе с алгоритмом оптимизации, чтобы попытаться найти глобальный минимум суммы квадратов.
Подробную информацию о нелинейном моделировании данных см. в разделе « Наименьшие квадраты» и «Нелинейный метод наименьших квадратов» .
В основе этой процедуры лежит предположение, что модель может быть аппроксимирована линейной функцией, а именно рядом Тейлора первого порядка :
где . Из этого следует, что оценки наименьших квадратов имеют вид
сравнить обобщенный метод наименьших квадратов с ковариационной матрицей, пропорциональной единичной матрице. Статистика нелинейной регрессии вычисляется и используется так же, как статистика линейной регрессии, но в формулах используется J вместо X.
Когда сама функция неизвестна аналитически, но ее необходимо линейно аппроксимировать из или более известных значений (где — количество оценщиков), лучшая оценка получается непосредственно из линейного шаблона, подходящего как [1]
Линейное приближение вносит систематическую ошибку в статистику. Поэтому при интерпретации статистики, полученной на основе нелинейной модели, требуется больше осторожности, чем обычно.
Часто предполагается, что наиболее подходящей кривой является та, которая минимизирует сумму квадратов остатков . Это обычный метод наименьших квадратов (МНК). Однако в случаях, когда зависимая переменная не имеет постоянной дисперсии, сумма взвешенных квадратов остатков может быть минимизирована; см. взвешенные наименьшие квадраты . В идеале каждый вес должен быть равен обратной величине дисперсии наблюдения, но веса могут пересчитываться на каждой итерации в итерационно взвешенном алгоритме наименьших квадратов.
Некоторые задачи нелинейной регрессии можно перенести в линейную область путем соответствующего преобразования формулировки модели.
Например, рассмотрим задачу нелинейной регрессии
с параметрами a и b и с мультипликативной ошибкой U. Если мы возьмем логарифм обеих частей, это станет
где u = ln( U ), что предполагает оценку неизвестных параметров посредством линейной регрессии ln( y ) по x , вычисление, которое не требует итеративной оптимизации. Однако использование нелинейного преобразования требует осторожности. Влияние значений данных изменится, равно как и структура ошибок модели и интерпретация любых логических выводов. Это могут быть нежелательные эффекты. С другой стороны, в зависимости от того, что является крупнейшим источником ошибок, нелинейное преобразование может распределять ошибки по Гауссу, поэтому выбор выполнения нелинейного преобразования должен основываться на соображениях моделирования.
Для кинетики Михаэлиса-Ментен линейный график Лайнуивера-Бёрка
соотношение 1/ v против 1/[ S ] широко использовалось. Однако, поскольку он очень чувствителен к ошибкам данных и сильно смещен в сторону соответствия данным определенному диапазону независимой переменной [ S ], его использование настоятельно не рекомендуется.
Для распределений ошибок, принадлежащих к экспоненциальному семейству , можно использовать функцию связи для преобразования параметров в рамках обобщенной линейной модели .
Независимую или объясняющую переменную (скажем, X) можно разделить на классы или сегменты, и для каждого сегмента можно выполнить линейную регрессию . Сегментированная регрессия с доверительным анализом может привести к тому, что зависимая переменная или переменная отклика (скажем, Y) ведет себя по-разному в различных сегментах. [2]
На рисунке видно, что засоление почвы (X) первоначально не оказывает влияния на урожайность культуры (Y) горчицы до достижения критического или порогового значения ( точки перелома ), после чего урожайность снижается отрицательно. [3]
![{\displaystyle {\frac {1}{v}}={\frac {1}{V_{\max }}}+{\frac {K_{m}}{V_{\max }[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb44905c5bb097edbf610f26176e996180c36ac7)
![{\displaystyle v={\frac {V_{\max }\ [{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb07a5f0c5464d685c5ab5072a8bee836260b6d)