Бета-распад

Тип радиоактивного распада

β⁻
 распад в атомном ядре (сопутствующее антинейтрино опущено). На вставке показан бета-распад свободного нейтрона. Ни одно из этих изображений не показывает промежуточный виртуальный Вт−бозон.

В ядерной физике бета -распад (β-распад) — это тип радиоактивного распада , при котором атомное ядро ​​испускает бета-частицу (быстрый энергичный электрон или позитрон ), превращаясь в изобару этого нуклида. Например, бета-распад нейтрона преобразует его в протон путем испускания электрона, сопровождаемого антинейтрино ; или, наоборот, протон превращается в нейтрон путем испускания позитрона с нейтрино в том, что называется испусканием позитрона . Ни бета-частица, ни связанное с ней (анти)нейтрино не существуют внутри ядра до бета-распада, но создаются в процессе распада. В результате этого процесса нестабильные атомы получают более стабильное соотношение протонов и нейтронов . Вероятность распада нуклида из-за бета-распада и других форм распада определяется его ядерной энергией связи . Энергии связи всех существующих нуклидов образуют то, что называется ядерной зоной или долиной стабильности . ^[1] Для того чтобы испускание электрона или позитрона было энергетически возможным, выделение энергии (см. ниже) или значение Q должны быть положительными.

Бета-распад является следствием слабого взаимодействия , которое характеризуется относительно долгим временем распада. Нуклоны состоят из верхних и нижних кварков , ^[2] и слабое взаимодействие позволяет кварку менять свой аромат путем испускания W-бозона , что приводит к созданию пары электрон/антинейтрино или позитрон/нейтрино. Например, нейтрон, состоящий из двух нижних кварков и верхнего кварка, распадается на протон, состоящий из нижнего кварка и двух верхних кварков.

Электронный захват иногда включают в число разновидностей бета-распада, ^[3], поскольку основной ядерный процесс, опосредованный слабым взаимодействием, тот же самый. При электронном захвате внутренний атомный электрон захватывается протоном в ядре, превращая его в нейтрон, и высвобождается электронное нейтрино .

Описание

Два типа бета-распада известны как бета-минус и бета-плюс . При бета-минус (β ⁻ ) распаде нейтрон преобразуется в протон, и в результате этого процесса образуются электрон и электронное антинейтрино ; в то время как при бета-плюс (β ⁺ ) распаде протон преобразуется в нейтрон, и в результате этого процесса образуются позитрон и электронное нейтрино. β ⁺ распад также известен как испускание позитрона . ^[4]

Бета-распад сохраняет квантовое число, известное как лептонное число , или число электронов и связанных с ними нейтрино (другие лептоны — это мюонные и тау -частицы). Эти частицы имеют лептонное число +1, в то время как их античастицы имеют лептонное число −1. Поскольку протон или нейтрон имеют лептонное число ноль, распад β ⁺ (позитрон или антиэлектрон) должен сопровождаться электронным нейтрино, в то время как распад β ⁻ (электрон) должен сопровождаться электронным антинейтрино.

Примером электронной эмиссии (β ^−- распада) является распад углерода-14 на азот-14 с периодом полураспада около 5730 лет:

¹⁴
₆С
→¹⁴
₇Н
+
е⁻
+
ν
_е

В этой форме распада исходный элемент становится новым химическим элементом в процессе, известном как ядерная трансмутация . Этот новый элемент имеет неизменное массовое число A , но атомный номер Z , который увеличивается на единицу. Как и во всех ядерных распадах, распадающийся элемент (в данном случае¹⁴
₆С
) известен как родительский нуклид, в то время как полученный элемент (в данном случае¹⁴
₇Н
) известен как дочерний нуклид .

Другим примером является распад водорода-3 ( трития ) в гелий-3 с периодом полураспада около 12,3 года:

³
₁ЧАС
→³
₂Он
+
е⁻
+
ν
_е

Примером позитронной эмиссии (β ⁺ -распад) является распад магния-23 в натрий-23 с периодом полураспада около 11,3 с:

²³
₁₂Мг
→²³
₁₁На
+
е⁺
+
ν
_е

Распад β ⁺ также приводит к ядерной трансмутации, в результате чего атомный номер образующегося элемента уменьшается на единицу.

Бета-спектр, показывающий типичное разделение энергии между электроном и антинейтрино.

Спектр бета-частиц, или распределение значений энергии для бета-частиц, является непрерывным. Полная энергия процесса распада делится между электроном, антинейтрино и откатывающимся нуклидом. На рисунке справа показан пример электрона с энергией 0,40 МэВ от бета-распада ^{210 Bi. В этом примере полная энергия распада составляет 1,16 МэВ, поэтому антинейтрино имеет оставшуюся энергию:} 1,16 МэВ − 0,40 МэВ = 0,76 МэВ . Электрон в крайней правой части кривой будет иметь максимально возможную кинетическую энергию, оставляя энергию нейтрино равной только его малой массе покоя.

История

Открытие и первоначальная характеристика

Радиоактивность была открыта в 1896 году Анри Беккерелем в уране , а впоследствии обнаружена Марией и Пьером Кюри в тории и в новых элементах полонии и радии . В 1899 году Эрнест Резерфорд разделил радиоактивные излучения на два типа: альфа и бета (теперь бета-минус), основываясь на проникновении сквозь объекты и способности вызывать ионизацию. Альфа-лучи могли быть остановлены тонкими листами бумаги или алюминия, тогда как бета-лучи могли проникать в несколько миллиметров алюминия. В 1900 году Поль Виллар идентифицировал еще более проникающий тип излучения, который Резерфорд определил как принципиально новый тип в 1903 году и назвал гамма-лучами . Альфа, бета и гамма — первые три буквы греческого алфавита .

В 1900 году Беккерель измерил отношение массы к заряду ( m / e ) для бета-частиц методом Дж. Дж. Томсона, который он использовал для изучения катодных лучей и идентификации электрона. Он обнаружил, что m / e для бета-частицы такое же, как и для электрона Томсона, и поэтому предположил, что бета-частица на самом деле является электроном. ^[5]

В 1901 году Резерфорд и Фредерик Содди показали, что альфа- и бета-радиоактивность включает в себя трансмутацию атомов в атомы других химических элементов. В 1913 году, после того как были известны продукты большего количества радиоактивных распадов, Содди и Казимеж Фаянс независимо предложили свой закон радиоактивного смещения , который гласит, что бета (т.е.
β⁻
) излучение одного элемента производит другой элемент, расположенный на одну позицию правее в периодической таблице , в то время как альфа-излучение производит элемент, расположенный на две позиции левее.

Нейтрино

Изучение бета-распада дало первое физическое доказательство существования нейтрино . Как при альфа-, так и при гамма-распаде результирующая альфа- или гамма-частица имеет узкое распределение энергии , поскольку частица переносит энергию из разницы между начальным и конечным ядерными состояниями. Однако распределение кинетической энергии, или спектр, бета-частиц, измеренное Лизой Мейтнер и Отто Ганом в 1911 году и Жаном Данишем в 1913 году, показало несколько линий на диффузном фоне. Эти измерения дали первый намек на то, что бета-частицы имеют непрерывный спектр. ^[6] В 1914 году Джеймс Чедвик использовал магнитный спектрометр с одним из новых счетчиков Ганса Гейгера, чтобы провести более точные измерения, которые показали, что спектр был непрерывным. ^{[6] [7]} Распределение энергий бета-частиц явно противоречило закону сохранения энергии . Если бы бета-распад был просто электронной эмиссией, как предполагалось в то время, то энергия испускаемого электрона должна была бы иметь конкретное, четко определенное значение. ^[8] Однако для бета-распада наблюдаемое широкое распределение энергий предполагает, что энергия теряется в процессе бета-распада. Этот спектр был загадкой в ​​течение многих лет.

Вторая проблема связана с сохранением углового момента . Молекулярные зонные спектры показали, что ядерный спин азота -14 равен 1 (т.е. равен приведенной постоянной Планка ) и, в более общем смысле, что спин является целым для ядер с четным массовым числом и полуцелым для ядер с нечетным массовым числом. Это было позже объяснено протонно-нейтронной моделью ядра . ^[8] Бета-распад оставляет массовое число неизменным, поэтому изменение ядерного спина должно быть целым числом. Однако спин электрона равен 1/2, поэтому угловой момент не сохранялся бы, если бы бета-распад был просто испусканием электронов.

С 1920 по 1927 год Чарльз Драммонд Эллис (вместе с Чедвиком и коллегами) дополнительно установил, что спектр бета-распада является непрерывным. В 1933 году Эллис и Невилл Мотт получили веские доказательства того, что бета-спектр имеет эффективную верхнюю границу по энергии. Нильс Бор предположил, что бета-спектр можно объяснить, если сохранение энергии верно только в статистическом смысле, таким образом, этот принцип может быть нарушен в любом данном распаде. ^{[8] : 27} Однако верхняя граница в бета-энергиях, определенная Эллисом и Моттом, исключила это представление. Теперь проблема того, как учесть изменчивость энергии в известных продуктах бета-распада, а также сохранение импульса и углового момента в этом процессе, стала острой.

В знаменитом письме, написанном в 1930 году, Вольфганг Паули попытался разрешить головоломку энергии бета-частиц, предположив, что, в дополнение к электронам и протонам, атомные ядра также содержат чрезвычайно легкую нейтральную частицу, которую он назвал нейтроном. Он предположил, что этот «нейтрон» также испускается во время бета-распада (таким образом, объясняя известную недостающую энергию, импульс и угловой момент), но он просто еще не был обнаружен. В 1931 году Энрико Ферми переименовал «нейтрон» Паули в «нейтрино» («маленький нейтральный» по-итальянски). В 1933 году Ферми опубликовал свою эпохальную теорию бета-распада , в которой он применил принципы квантовой механики к частицам материи, предположив, что они могут создаваться и уничтожаться, как и кванты света при атомных переходах. Таким образом, по Ферми, нейтрино создаются в процессе бета-распада, а не содержатся в ядре; то же самое происходит с электронами. Взаимодействие нейтрино с материей было настолько слабым, что его обнаружение оказалось серьезной экспериментальной проблемой. Дальнейшие косвенные доказательства существования нейтрино были получены путем наблюдения за отдачей ядер, которые испускали такую ​​частицу после поглощения электрона. Нейтрино были окончательно обнаружены непосредственно в 1956 году американскими физиками Клайдом Коуэном и Фредериком Райнесом в нейтринном эксперименте Коуэна–Райнеса . ^[9] Свойства нейтрино были (с несколькими незначительными изменениями) такими, как предсказывали Паули и Ферми.

β+ распад и захват электронов

В 1934 году Фредерик и Ирен Жолио-Кюри бомбардировали алюминий альфа-частицами, чтобы вызвать ядерную реакцию.⁴
₂Он
 + ²⁷
₁₃Эл
 →³⁰
₁₅П
 + ¹
₀н
, и заметил, что продукт изотоп³⁰
₁₅П
испускает позитрон, идентичный тем, которые обнаружены в космических лучах (открытых Карлом Дэвидом Андерсоном в 1932 году). Это был первый пример
β⁺
 распад ( эмиссию позитронов ), который они назвали искусственной радиоактивностью, поскольку³⁰
₁₅П
это короткоживущий нуклид, который не существует в природе. В знак признания их открытия пара была удостоена Нобелевской премии по химии в 1935 году . ^[10]

Теория захвата электронов была впервые обсуждена Джан-Карло Виком в статье 1934 года, а затем развита Хидеки Юкавой и другими. Захват K-электронов впервые наблюдал в 1937 году Луис Альварес в нуклиде ^48V . ^{[11] [12] [13]} Альварес продолжил изучать захват электронов в ⁶⁷ Ga и других нуклидах. ^{[11] [14] [15]}

Несохранение четности

В 1956 году Цзун-Дао Ли и Чэнь Нин Ян заметили, что нет никаких доказательств того, что четность сохраняется в слабых взаимодействиях, и поэтому они постулировали, что эта симметрия может не сохраняться слабой силой. Они набросали схему эксперимента по проверке сохранения четности в лабораторных условиях. ^[16] Позже в том же году Цзянь-Шюн Ву и его коллеги провели эксперимент Ву, показав асимметричный бета-распад60Копри низких температурах, что доказало, что четность не сохраняется в бета-распаде. ^{[17] [18]} Этот удивительный результат перевернул давние предположения о четности и слабом взаимодействии. В знак признания их теоретической работы Ли и Янг были награждены Нобелевской премией по физике в 1957 году. Однако Ву, которая была женщиной, не была удостоена Нобелевской премии. ^[19]

β−разлагаться

Диаграмма Фейнмана ведущего порядка для
β⁻
 распад нейтрона на протон , электрон и электронное антинейтрино через промежуточное вещество
Вт⁻
Бозон . Для диаграмм более высокого порядка см. ^{[20] [21]}

В
β⁻
 распад, слабое взаимодействие преобразует атомное ядро ​​в ядро ​​с атомным номером , увеличенным на единицу, испуская при этом электрон (е−) и электронное антинейтрино (
ν
_е).
β⁻
 Распад обычно происходит в ядрах, богатых нейтронами. ^[22] Общее уравнение выглядит так:

^А
_ЯХ
→^А
_{Я +1}Х′
+
е⁻
+
ν
_е^[1]

где A и Z — массовое число и атомный номер распадающегося ядра, а X и X′ — начальный и конечный элементы соответственно.

Другой пример — когда свободный нейтрон (¹
₀н
) распадается на
β⁻
 распадается на протон (
п
):

н
→
п
+
е⁻
+
ν
_е.

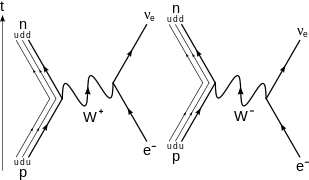
На фундаментальном уровне (как показано на диаграмме Фейнмана справа) это вызвано преобразованием отрицательно заряженного ( − ⁠1/3⁠ e ) нижний кварк до положительно заряженного ( + ⁠2/3⁠ e ) ап-кварк путем испускания
Вт⁻
бозон ;
Вт⁻
Бозон впоследствии распадается на электрон и электронное антинейтрино:

г
→
ты
+
е⁻
+
ν
_е.

β+разлагаться

Диаграмма Фейнмана ведущего порядка для
β⁺
 распад протона на нейтрон , позитрон и электронное нейтрино через промежуточное вещество
Вт⁺
бозон

В
β⁺
 распад, или испускание позитрона, слабое взаимодействие преобразует атомное ядро ​​в ядро ​​с атомным номером, уменьшенным на единицу, испуская при этом позитрон (
е⁺
) и электронное нейтрино (
ν
_е).
β⁺
 Распад обычно происходит в протон-богатых ядрах. Общее уравнение:

^А
_ЯХ
→^А
_{Я −1}Х′
+
е⁺
+
ν
_е^[1]

Это можно рассматривать как распад протона внутри ядра на нейтрон:

п → н +
е⁺
+
ν
_е^[1]

Однако,
β⁺
 Распад не может происходить в изолированном протоне, поскольку для этого требуется энергия, поскольку масса нейтрона больше массы протона.
β⁺
 Распад может происходить только внутри ядер, когда дочернее ядро ​​имеет большую энергию связи (и, следовательно, меньшую полную энергию), чем материнское ядро. Разница между этими энергиями входит в реакцию превращения протона в нейтрон, позитрон и нейтрино и в кинетическую энергию этих частиц. Этот процесс противоположен отрицательному бета-распаду, в котором слабое взаимодействие превращает протон в нейтрон, превращая верхний кварк в нижний кварк, что приводит к испусканию
Вт⁺
или поглощение
Вт⁻
. Когда
Вт⁺
Бозон испускается, распадается на позитрон и электронное нейтрино :

ты
→
г
+
е⁺
+
ν
_е.

Захват электронов (К-захват/L-захват)

Диаграммы Фейнмана ведущего порядка для распада электронного захвата . Электрон взаимодействует с верхним кварком в ядре через W-бозон , создавая нижний кварк и электронное нейтрино . Две диаграммы составляют ведущий (второй) порядок, хотя как виртуальная частица тип (и заряд) W-бозона неразличимы.

Во всех случаях, когда
β⁺
 Распад (испускание позитрона) ядра энергетически разрешен, также разрешен захват электронов . Это процесс, в ходе которого ядро ​​захватывает один из своих атомных электронов, что приводит к испусканию нейтрино:

^А
_ЯХ
+
е⁻
→^А
_{Я −1}Х′
+
ν
_е

Примером электронного захвата является один из способов распада криптона-81 на бром-81 :

⁸¹
₃₆Кр
+
е⁻
→⁸¹
₃₅Бр
+
ν
_е

Все испускаемые нейтрино имеют одинаковую энергию. В протонно-богатых ядрах, где разница энергий между начальным и конечным состояниями меньше 2 m _e c ² ,
β⁺
 Распад энергетически невозможен, и захват электронов является единственным способом распада. ^[23]

Если захваченный электрон исходит из самой внутренней оболочки атома, K-оболочки , которая имеет наибольшую вероятность взаимодействия с ядром, процесс называется K-захватом. ^[24] Если он исходит из L-оболочки, процесс называется L-захватом и т. д.

Захват электронов является конкурирующим (одновременным) процессом распада для всех ядер, которые могут подвергаться β ⁺ распаду. Обратное, однако, неверно: захват электронов является единственным типом распада, который разрешен в богатых протонами нуклидах, которые не обладают достаточной энергией для испускания позитрона и нейтрино. ^[23]

Ядерная трансмутация

График изотопов по типу ядерного распада. Оранжевые и синие нуклиды нестабильны, а черные квадраты между этими областями представляют стабильные нуклиды. Сплошная линия, проходящая под многими нуклидами, представляет теоретическую позицию на графике нуклидов, для которых число протонов равно числу нейтронов. График показывает, что элементы с более чем 20 протонами должны иметь больше нейтронов, чем протонов, чтобы быть стабильными.

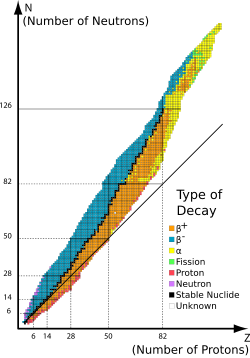
Если протон и нейтрон являются частью атомного ядра , то описанные выше процессы распада преобразуют один химический элемент в другой. Например:

Бета-распад не изменяет число ( A ) нуклонов в ядре, а изменяет только его заряд  Z . Таким образом, можно ввести набор всех нуклидов с одинаковым  A ; эти изобарные нуклиды могут превращаться друг в друга посредством бета-распада. Для заданного A есть один, который наиболее стабилен. Он называется бета-стабильным, потому что он представляет локальный минимум избытка массы : если такое ядро ​​имеет числа ( A , Z ) , соседние ядра ( A , Z −1) и ( A , Z +1) имеют более высокий избыток массы и могут бета-распасться в ( A , Z ) , но не наоборот. Для всех нечетных массовых чисел A , существует только одна известная бета-стабильная изобара. Для четных  A , существует до трех различных бета-стабильных изобар экспериментально известных ; например,¹²⁴
₅₀Сн
,¹²⁴
₅₂Те
, и¹²⁴
₅₄Хе
все бета-стабильны. Известно около 350 стабильных по бета-распаду нуклидов . ^[25]

Конкуренция типов бета-распада

Обычно нестабильные нуклиды явно либо «богаты нейтронами», либо «богаты протонами», причем первые подвергаются бета-распаду, а вторые — электронному захвату (или, что реже, из-за более высоких энергетических требований, позитронному распаду). Однако в некоторых случаях нечетно-протонных, нечетно-нейтронных радионуклидов может быть энергетически выгодно, чтобы радионуклид распался до четно-протонной, четно-нейтронной изобары либо путем бета-положительного, либо бета-отрицательного распада. Часто приводимым примером является один изотоп⁶⁴
₂₉Cu
(29 протонов, 35 нейтронов), что иллюстрирует три типа бета-распада в конкуренции. Период полураспада меди-64 составляет около 12,7 часов. Этот изотоп имеет один неспаренный протон и один неспаренный нейтрон, поэтому либо протон, либо нейтрон может распадаться. Этот конкретный нуклид (хотя и не все нуклиды в этой ситуации) почти в равной степени склонен распадаться через протонный распад путем испускания позитрона (18% ) или захват электронов (43% ) к⁶⁴
₂₈Ни
, как это происходит через распад нейтрона путем испускания электронов (39% ) к⁶⁴
₃₀Zn
. ^[26]

Стабильность природных нуклидов

Большинство естественных нуклидов на Земле являются бета-стабильными. Нуклиды, которые не являются бета-стабильными, имеют периоды полураспада от менее секунды до периодов времени, значительно превышающих возраст Вселенной . Одним из распространенных примеров долгоживущего изотопа является нечетно-протонный нечетно-нейтронный нуклид⁴⁰
₁₉К
, который претерпевает все три типа бета-распада (
β⁻
,
β⁺
и захват электронов) с периодом полураспада1,277 × 10 ⁹  лет . ^[27]

Правила сохранения для бета-распада

Число барионов сохраняется

$${\displaystyle B={\frac {n_{q}-n_{\bar {q}}}{3}}}$$где

• ${\displaystyle n_{q}}$- это число составляющих кварков, а
• ${\displaystyle n_{\overline {q}}}$— число составляющих антикварков.

Бета-распад просто меняет нейтрон на протон или, в случае положительного бета-распада ( электронного захвата ), протон на нейтрон, так что число отдельных кварков не меняется. Изменяется только аромат бариона, здесь обозначенный как изоспин .

Верхние и нижние кварки имеют полный изоспин и проекции изоспина ${\textstyle I={\frac {1}{2}}}$ $${\displaystyle I_{\text{z}}={\begin{cases}{\frac {1}{2}}&{\text{up quark}}\\-{\frac {1}{2}}&{\text{down quark}}\end{cases}}}$$

Все остальные кварки имеют I = 0 .

В общем $${\displaystyle I_{\text{z}}={\frac {1}{2}}(n_{\text{u}}-n_{\text{d}})}$$

Число лептонов сохраняется

$${\displaystyle L\equiv n_{\ell }-n_{\bar {\ell }}}$$

поэтому всем лептонам присвоено значение +1, антилептонам −1, а нелептонным частицам 0. $${\displaystyle {\begin{matrix}&{\text{n}}&\rightarrow &{\text{p}}&+&{\text{e}}^{-}&+&{\bar {\nu }}_{\text{e}}\\L:&0&=&0&+&1&-&1\end{matrix}}}$$

Угловой момент импульса

Для разрешенных распадов суммарный орбитальный угловой момент равен нулю, поэтому рассматриваются только спиновые квантовые числа.

Электрон и антинейтрино являются фермионами , объектами со спином 1/2, поэтому они могут взаимодействовать полностью (параллельно) или (антипараллельно). ${\displaystyle S=1}$ ${\displaystyle S=0}$

Для запрещенных распадов необходимо также учитывать орбитальный угловой момент.

Выделение энергии

Значение Q определяется как полная энергия, высвобождаемая при данном ядерном распаде. Таким образом, при бета-распаде Q также является суммой кинетических энергий испускаемой бета-частицы, нейтрино и отскакивающего ядра. (Из-за большой массы ядра по сравнению с массой бета-частицы и нейтрино кинетической энергией отскакивающего ядра обычно можно пренебречь.) Поэтому бета-частицы могут испускаться с любой кинетической энергией в диапазоне от 0 до Q. ^[1] Типичное значение Q составляет около 1  МэВ , но может варьироваться от нескольких кэВ до нескольких десятков МэВ.

Поскольку масса покоя электрона составляет 511 кэВ, наиболее энергичные бета-частицы являются ультрарелятивистскими , со скоростями, очень близкими к скорости света . В случае ¹⁸⁷ Re максимальная скорость бета-частицы составляет всего 9,8% от скорости света.

В следующей таблице приведены некоторые примеры:

β−разлагаться

Рассмотрим общее уравнение бета-распада

^А
_ЯХ
→^А
_{Я +1}Х′
+
е⁻
+
ν
_е.

Значение Q для этого распада равно

${\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)-m_{e}-m_{{\overline {\nu }}_{e}}\right]c^{2}}$,

где - масса ядра ${\displaystyle m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)}$^А
_ЯХ
атом, - масса электрона, - масса электронного антинейтрино. Другими словами, полная высвобождаемая энергия - это массовая энергия начального ядра за вычетом массовой энергии конечного ядра, электрона и антинейтрино. Масса ядра m _N связана со стандартной атомной массой m соотношением То есть полная атомная масса - это масса ядра плюс масса электронов за вычетом суммы всех энергий связи электронов B _i для атома. Это уравнение перестраивается, чтобы найти , и находится аналогично. Подставляя эти ядерные массы в уравнение для значения Q , пренебрегая при этом почти нулевой массой антинейтрино и разницей в энергиях связи электронов, которая очень мала для атомов с высоким Z , мы имеем Эта энергия уносится в виде кинетической энергии электроном и антинейтрино. ${\displaystyle m_{e}}$ ${\displaystyle m_{{\overline {\nu }}_{e}}}$ $${\displaystyle m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)c^{2}=m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)c^{2}+Zm_{e}c^{2}-\sum _{i=1}^{Z}B_{i}.}$$ ${\displaystyle m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)}$ ${\displaystyle m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)}$ $${\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)\right]c^{2}}$$

Поскольку реакция будет протекать только тогда, когда значение Q  положительно, β ⁻ распад может происходить, когда масса атома^А
_ЯХ
больше массы атома^А
_{Я +1}Х′
. ^[28]

β+разлагаться

Уравнения для β ⁺ распада аналогичны, с общим уравнением

^А
_ЯХ
→^А
_{Я −1}Х′
+
е⁺
+
ν
_е

давая Однако в этом уравнении массы электронов не сокращаются, и у нас остается $${\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-m_{e}-m_{\nu _{e}}\right]c^{2}.}$$ $${\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-2m_{e}\right]c^{2}.}$$

Поскольку реакция будет протекать только тогда, когда значение Q  положительно, β ⁺ распад может происходить, когда масса атома^А
_ЯХ
превышает^А
_{Я -1}Х′
по крайней мере вдвое больше массы электрона. ^[28]

Захват электронов

Аналогичный расчет для захвата электрона должен учитывать энергию связи электронов. Это происходит потому, что атом останется в возбужденном состоянии после захвата электрона, а энергия связи захваченного внутреннего электрона значительна. Используя общее уравнение для захвата электрона

^А
_ЯХ
+
е⁻
→^А
_{Я −1}Х′
+
ν
_е

имеем что упрощается до где B _n — энергия связи захваченного электрона. $${\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)+m_{e}-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-m_{\nu _{e}}\right]c^{2},}$$ $${\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)\right]c^{2}-B_{n},}$$

Поскольку энергия связи электрона намного меньше массы электрона, ядра, которые могут подвергаться β ⁺ -распаду, всегда могут также подвергаться электронному захвату, но обратное неверно. ^[28]

Спектр бета-излучения

Бета-спектр ²¹⁰ Bi. E _max = Q = 1,16 МэВ — максимальная энергия

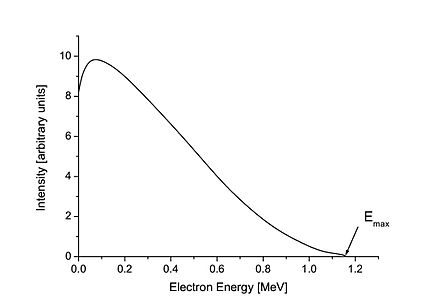
Бета-распад можно рассматривать как возмущение , как описано в квантовой механике, и, таким образом, можно применить Золотое правило Ферми . Это приводит к следующему выражению для спектра кинетической энергии N ( T ) испускаемых бета-частиц: ^[29]

$${\displaystyle N(T)=C_{L}(T)F(Z,T)pE(Q-T)^{2}}$$

где T — кинетическая энергия, C _L — функция формы, зависящая от запрета распада (она постоянна для разрешенных распадов), F ( Z , T ) — функция Ферми (см. ниже), где Z — заряд ядра в конечном состоянии, E = T + mc ² — полная энергия, — импульс, а Q — значение Q распада. Кинетическая энергия испускаемого нейтрино приблизительно определяется как Q минус кинетическая энергия бета. ${\displaystyle p={\sqrt {(E/c)^{2}-(mc)^{2}}}}$

В качестве примера справа показан спектр бета-распада ^{210Bi (первоначально называвшегося RaE).}

Функция Ферми

Функция Ферми, которая появляется в формуле бета-спектра, учитывает кулоновское притяжение/отталкивание между испускаемой бета-частицей и конечным ядром. Приближая связанные волновые функции к сферически-симметричным, можно аналитически рассчитать функцию Ферми следующим образом: ^[30]

$${\displaystyle F(Z,T)={\frac {2(1+S)}{\Gamma (1+2S)^{2}}}(2p\rho )^{2S-2}e^{\pi \eta }|\Gamma (S+i\eta )|^{2},}$$

где p — конечный импульс, Γ — гамма-функция , и (если α — постоянная тонкой структуры , а r _N — радиус ядра конечного состояния) , (+ для электронов, − для позитронов), и . ${\displaystyle S={\sqrt {1-\alpha ^{2}Z^{2}}}}$ ${\displaystyle \eta =\pm Ze^{2}E/(\hbar cp)}$ ${\displaystyle \rho =r_{N}/\hbar }$

Для нерелятивистских бета-частиц ( Q ≪ m _e c ² ) это выражение можно аппроксимировать следующим образом: ^[31]

$${\displaystyle F(Z,T)\approx {\frac {2\pi \eta }{1-e^{-2\pi \eta }}}.}$$

Другие приближения можно найти в литературе. ^{[32] [33]}

участок Кюри

График Кюри (также известный как график Ферми–Кюри ) — это график, используемый при изучении бета-распада, разработанный Францем Н. Д. Кюри , на котором квадратный корень из числа бета-частиц, импульсы (или энергия) которых лежат в определенном узком диапазоне, деленный на функцию Ферми, откладывается в зависимости от энергии бета-частицы. ^{[34] [35]} Это прямая линия для разрешенных переходов и некоторых запрещенных переходов в соответствии с теорией бета-распада Ферми. Пересечение оси энергии (оси x) графика Кюри соответствует максимальной энергии, переданной электрону/позитрону ( значение Q распада  ). С помощью графика Кюри можно найти предел эффективной массы нейтрино. ^[36]

Спиральность (поляризация) нейтрино, электронов и позитронов, испускаемых при бета-распаде

После открытия несохранения четности (см. Историю) было обнаружено, что при бета-распаде электроны испускаются в основном с отрицательной спиральностью , т. е. они движутся, наивно говоря, как левовинтовые винты, ввинченные в материал (они имеют отрицательную продольную поляризацию ). ^[37] Наоборот, позитроны имеют в основном положительную спиральность, т. е. они движутся как правовинтовые винты. Нейтрино (испускаемые при распаде позитрона) имеют отрицательную спиральность, в то время как антинейтрино (испускаемые при распаде электрона) имеют положительную спиральность. ^[38]

Чем выше энергия частиц, тем выше их поляризация.

Типы бета-распадных переходов

Бета-распады можно классифицировать по угловому моменту (  значение L ) и полному спину (  значение S ) испускаемого излучения. Поскольку полный угловой момент должен сохраняться, включая орбитальный и спиновый угловой момент, бета-распад происходит посредством множества переходов квантовых состояний в различные ядерные угловые моменты или спиновые состояния, известные как переходы «Ферми» или «Гамова–Теллера». Когда частицы бета-распада не несут углового момента ( L = 0 ), распад называется «разрешенным», в противном случае он «запрещен».

Другие виды распада, которые встречаются редко, известны как распад связанного состояния и двойной бета-распад.

Ферми-переходы

Переход Ферми — это бета-распад, в котором спины испускаемого электрона (позитрона) и антинейтрино (нейтрино) связываются с общим спином , что приводит к изменению углового момента между начальным и конечным состояниями ядра (предполагая разрешенный переход). В нерелятивистском пределе ядерная часть оператора для перехода Ферми задается с константой слабой векторной связи, изоспиновыми повышающими и понижающими операторами и пробегающими по всем протонам и нейтронам в ядре. ${\displaystyle S=0}$ ${\displaystyle \Delta J=0}$ $${\displaystyle {\mathcal {O}}_{F}=G_{V}\sum _{a}{\hat {\tau }}_{a\pm }}$$ ${\displaystyle G_{V}}$ ${\displaystyle \tau _{\pm }}$ ${\displaystyle a}$

Переходы Гамова-Теллера

Переход Гамова -Теллера представляет собой бета-распад, в котором спины испускаемого электрона (позитрона) и антинейтрино (нейтрино) связываются с общим спином , что приводит к изменению углового момента между начальным и конечным состояниями ядра (предполагая разрешенный переход). В этом случае ядерная часть оператора задается с константой слабой аксиально-векторной связи и спиновыми матрицами Паули , которые могут вызывать переворот спина в распадающемся нуклоне. ${\displaystyle S=1}$ ${\displaystyle \Delta J=0,\pm 1}$ $${\displaystyle {\mathcal {O}}_{GT}=G_{A}\sum _{a}{\hat {\sigma }}_{a}{\hat {\tau }}_{a\pm }}$$ ${\displaystyle G_{A}}$ ${\displaystyle \sigma }$

Запрещенные переходы

Когда L > 0 , распад называется « запрещенным ». Правила ядерного отбора требуют, чтобы высокие значения L  сопровождались изменениями ядерного спина  ( J ) и четности  ( π ). Правила отбора для запрещенных переходов L следующие: где Δ π = 1 или −1 соответствует отсутствию изменения четности или изменению четности соответственно. Особый случай перехода между изобарическими аналоговыми состояниями, где структура конечного состояния очень похожа на структуру начального состояния, называется «сверхразрешенным» для бета-распада и происходит очень быстро. В следующей таблице перечислены значения Δ J и Δ π для первых нескольких значений  L : $${\displaystyle \Delta J=L-1,L,L+1;\Delta \pi =(-1)^{L},}$$

Редкие режимы распада

Связанное состояние β−разлагаться

Очень небольшое количество свободных нейтронных распадов (около четырех на миллион) представляют собой так называемые «двухчастичные распады», в которых образуются протон, электрон и антинейтрино, но электрон не может получить энергию 13,6 эВ, необходимую для того, чтобы покинуть протон, и поэтому просто остается связанным с ним, как нейтральный атом водорода . ^{[39] В этом типе бета-распада, по сути, вся} энергия распада нейтрона уносится антинейтрино.

Для полностью ионизированных атомов (голых ядер) аналогичным образом возможно, что электроны не покинут атом и будут испущены из ядра в низколежащие атомные связанные состояния (орбитали). Это не может произойти для нейтральных атомов с низколежащими связанными состояниями, которые уже заполнены электронами.

Связанные β-распады были предсказаны Дауделем , Жаном и Лекойном в 1947 году ^[40] , а явление в полностью ионизированных атомах впервые наблюдалось для ¹⁶³ Dy ⁶⁶⁺ в 1992 году Юнгом и др. из Дармштадтского центра исследований тяжелых ионов . Хотя нейтральные¹⁶³
Dy является стабильным изотопом, полностью ионизированный ¹⁶³ Dy ⁶⁶⁺ подвергается β-распаду на оболочки K и L с периодом полураспада 47 дней. ^[41] Полученное ядро ​​–¹⁶³
Ho – стабилен только в полностью ионизированном состоянии и распадается посредством электронного захвата на¹⁶³
Dy в нейтральном состоянии. Период полураспада для нейтрального¹⁶³
Ho — 4750 лет.

Другая возможность заключается в том, что полностью ионизированный атом подвергается значительно ускоренному β-распаду, как это наблюдалось для ¹⁸⁷ Re Бошем и др. также в Дармштадте. Нейтральный ¹⁸⁷ Re подвергается β-распаду с периодом полураспада41,6 × 10 ⁹  лет, ^[42] но для полностью ионизированного ¹⁸⁷ Re ⁷⁵⁺ этот период сокращается до всего лишь 32,9 лет. ^[43] Для сравнения, изменение скоростей распада других ядерных процессов из-за химической среды составляет менее 1% .

Двойной бета-распад

Некоторые ядра могут подвергаться двойному бета-распаду (ββ-распаду), при котором заряд ядра изменяется на две единицы. Двойной бета-распад трудно изучать, так как этот процесс имеет чрезвычайно большой период полураспада. В ядрах, для которых возможны как β-распад, так и ββ-распад, более редкий процесс ββ-распада фактически невозможно наблюдать. Однако в ядрах, где β-распад запрещен, но ββ-распад разрешен, процесс можно увидеть и измерить период полураспада. ^[44] Таким образом, ββ-распад обычно изучается только для бета-стабильных ядер. Как и одинарный бета-распад, двойной бета-распад не изменяет A ; таким образом, по крайней мере один из нуклидов с некоторым заданным A должен быть стабильным относительно как одинарного, так и двойного бета-распада.

«Обычный» двойной бета-распад приводит к испусканию двух электронов и двух антинейтрино. Если нейтрино являются частицами Майораны (т. е. они являются своими собственными античастицами), то произойдет распад, известный как безнейтринный двойной бета-распад . Большинство физиков, изучающих нейтрино, считают, что безнейтринный двойной бета-распад никогда не наблюдался. ^[44]

Смотрите также

• Распространенные бета-излучатели
• Нейтрино
• Бетавольтаика
• Корпускулярное излучение
• Радионуклид
• Тритиевое освещение , вид флуоресцентного освещения, работающего на бета-распаде.
• Эффект Пандемониума
• Спектроскопия полного поглощения

Ссылки

1. Конья, Дж.; Надь, Н. М. (2012). Ядерная и радиохимия . Elsevier . стр. 74–75. ISBN 978-0-12-391487-3.
2. Bijker, R.; Santopinto, E. (2015). «Валентность и морские кварки в нуклоне». Journal of Physics: Conference Series . 578 (1): 012015. arXiv : 1412.5559 . Bibcode : 2015JPhCS.578a2015B. doi : 10.1088/1742-6596/578/1/012015. S2CID  118499855.
3. Cottingham, WN; Greenwood, DA (1986). Введение в ядерную физику. Cambridge University Press . стр. 40. ISBN 978-0-521-31960-7.
4. Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Основы ядерной физики: от структуры ядра до космологии . Springer . ISBN 978-0-387-01672-6.
5. L'Annunziata, Michael (2012). Справочник по анализу радиоактивности (третье изд.). Elsevier Inc. стр. 3. ISBN 978-0-12-384874-1. Получено 4 октября 2017 г.
6. Jensen, C. (2000). Противоречия и консенсус: ядерный бета-распад 1911-1934. Birkhäuser Verlag . ISBN 978-3-7643-5313-1.
7. Чедвик, Дж. (1914). «Интенсивное магнитное излучение β-стралена радия B + C». Verhandlungen der Deutschen Physikalischen Gesellschaft (на немецком языке). 16 : 383–391.
8. Brown, LM (1978). «Идея нейтрино». Physics Today . 31 (9): 23–8. Bibcode : 1978PhT....31i..23B. doi : 10.1063/1.2995181.
9. Коуэн, CL Jr.; Рейнес, F.; Харрисон, FB; Круз, HW; МакГвайр, AD (1956). «Обнаружение свободного нейтрино: подтверждение». Science . 124 (3212): 103–104. Bibcode :1956Sci...124..103C. doi :10.1126/science.124.3212.103. PMID  17796274.
10. "Нобелевская премия по химии 1935 года". www.nobelprize.org . Получено 25.04.2018 .
11. Segré, E. (1987). "K-Electron Capture by Nuclei". В Trower, PW (ред.). Discovering Alvarez: Selected Works of Luis W. Alvarez . University of Chicago Press . стр. 11–12. ISBN 978-0-226-81304-2.
12. "Нобелевская премия по физике 1968: Луис Альварес". Нобелевский фонд . Получено 2009-10-07 .
13. Альварес, Л. В. (1937). «Ядерный захват электронов K». Physical Review . 52 (2): 134–135. Bibcode : 1937PhRv...52..134A. doi : 10.1103/PhysRev.52.134.
14. Альварес, Л. В. (1938). «Захват электронов и внутренняя конверсия в галлии 67». Physical Review . 53 (7): 606. Bibcode : 1938PhRv...53..606A. doi : 10.1103/PhysRev.53.606.
15. Альварес, Л. В. (1938). «Захват орбитальных электронов ядрами». Physical Review . 54 (7): 486–497. Bibcode : 1938PhRv...54..486A. doi : 10.1103/PhysRev.54.486.
16. Ли, ТД; Янг, КН (1956). «Вопрос сохранения четности в слабых взаимодействиях». Physical Review . 104 (1): 254–258. Bibcode :1956PhRv..104..254L. doi : 10.1103/PhysRev.104.254 .
17. Wu, C.-S.; Ambler, E.; Hayward, RW; Hoppes, DD; Hudson, RP (1957). «Экспериментальная проверка сохранения четности при бета-распаде». Physical Review . 105 (4): 1413–1415. Bibcode :1957PhRv..105.1413W. doi : 10.1103/PhysRev.105.1413 .
18. Вайншток, Майя. «Воплощение Ады Лавлейс: Цзяньсюн У, мужественный герой физики». scientificamerican.com .
19. "Нобелевская премия по физике 1957 года". Нобелевский фонд . Получено 24 марта 2015 г.
20. Иванов, АН; Хёлльвизер, Р.; Троицкая, Н.И.; Веллензон, М.; Бердников, Я. А. (26 июня 2017 г.). «Прецизионный теоретический анализ радиационного бета-распада нейтрона порядка O ( α 2 / π 2 )». Физический обзор D . 95 (11): 113006. arXiv : 1706.08687 . Бибкод : 2017PhRvD..95k3006I. doi : 10.1103/PhysRevD.95.113006. ISSN  2470-0010. S2CID  119103283.
21. Иванов, АН; Хёльвизер, Р.; Троицкая, НИ; Веллензон, М.; Бердников, Я. А. (2018-11-30). "Калибровочные свойства адронной структуры нуклона в нейтронном радиационном бета-распаде до порядка O(α/π) в стандартном V – Эффективная теория с КЭД и линейной сигма-моделью сильных низкоэнергетических взаимодействий". International Journal of Modern Physics A . 33 (33): 1850199. arXiv : 1805.09702 . Bibcode :2018IJMPA..3350199I. doi :10.1142/S0217751X18501993. ISSN  0217-751X. S2CID  119088802.
22. Лавленд, У. Д. (2005). Современная ядерная химия. Wiley . стр. 232. ISBN 978-0-471-11532-8.
23. Зубер, К. (2011). Нейтринная физика (2-е изд.). ЦРК Пресс . п. 466. ИСБН 978-1-4200-6471-1.
24. Евремович, Т. (2009). Ядерные принципы в инженерии. Springer Science + Business Media . стр. 201. ISBN 978-0-387-85608-7.
25. "Интерактивная карта нуклидов". Национальный центр ядерных данных, Брукхейвенская национальная лаборатория. Архивировано из оригинала 2018-10-10 . Получено 2014-09-18 .
26. "WWW Таблица радиоактивных изотопов, медь 64". LBNL Isotopes Project . Национальная лаборатория Лоуренса в Беркли. Архивировано из оригинала 2013-12-14 . Получено 2014-09-18 .
27. "WWW Таблица радиоактивных изотопов, калий 40". LBNL Isotopes Project . Национальная лаборатория Лоуренса в Беркли. Архивировано из оригинала 2013-10-09 . Получено 2014-09-18 .
28. Kenneth S. Krane (5 ноября 1987 г.). Введение в ядерную физику. Wiley. ISBN 978-0-471-80553-3.
29. Nave, CR "Энергетические и импульсные спектры для бета-распада". HyperPhysics . Получено 2013-03-09 .
30. Ферми, Э. (1934). "Versuch einer Theorie der β-Strahlen. I". Zeitschrift für Physik . 88 (3–4): 161–177. Бибкод : 1934ZPhy...88..161F. дои : 10.1007/BF01351864. S2CID  125763380.
31. Мотт, Н. Ф.; Мэсси, Х. С. У. (1933). Теория атомных столкновений . Clarendon Press . LCCN  34001940.
32. Venkataramaiah, P.; Gopala, K.; Basavaraju, A.; Suryanarayana, SS; Sanjeeviah, H. (1985). "Простое соотношение для функции Ферми". Journal of Physics G. 11 ( 3): 359–364. Bibcode :1985JPhG...11..359V. doi :10.1088/0305-4616/11/3/014. S2CID  250803189.
33. Schenter, GK; Vogel, P. (1983). "Простая аппроксимация функции Ферми в ядерном бета-распаде". Nuclear Science and Engineering . 83 (3): 393–396. Bibcode :1983NSE....83..393S. doi :10.13182/NSE83-A17574. OSTI  5307377.
34. Кьюри, ФНД ; Ричардсон, Дж. Р.; Пакстон, Х. К. (1936). «Излучения, испускаемые искусственно созданными радиоактивными веществами. I. Верхние пределы и формы спектров β-лучей от нескольких элементов». Physical Review . 49 (5): 368–381. Bibcode : 1936PhRv...49..368K. doi : 10.1103/PhysRev.49.368.
35. Кьюри, ФНД (1948). «Об использовании графика Кьюри». Physical Review . 73 (10): 1207. Bibcode : 1948PhRv...73.1207K. doi : 10.1103/PhysRev.73.1207.
36. Rodejohann, W. (2012). "Безнейтринный двойной бета-распад и физика нейтрино". Journal of Physics G: Nuclear and Particle Physics . 39 (12): 124008. arXiv : 1206.2560 . Bibcode :2012JPhG...39l4008R. doi :10.1088/0954-3899/39/12/124008. S2CID  119158221.
37. Фрауэнфельдер, Х.; и др. (1957). «Четность и поляризация электронов из Co60». Physical Review . 106 (2): 386–387. Bibcode : 1957PhRv..106..386F. doi : 10.1103/physrev.106.386.
38. Конопински, Э. Дж.; Роуз, М. Э. (1966). «Теория ядерного бета-распада». В Siegbhan, К. (ред.). Альфа-, бета- и гамма-спектроскопия . Т. 2. North-Holland Publishing Company .
39. Обзор распада нейтрона. Архивировано 19 сентября 2017 г. на Wayback Machine. Дж. Бирн в Quark-Mixing, CKM Unitarity (H. Abele и D. Mund, 2002), см. стр. XV.
40. Даудель, Раймонд; Жан, Морис; Лекуан, Марсель (1947). «Sur la possibilité d'existence d'un type of speculier de radioactivité Phénomène de Creation e». Дж. Физ. Радий . 8 (8): 238–243. doi : 10.1051/jphysrad: 0194700808023800.
41. Юнг, М.; и др. (1992). «Первое наблюдение связанного состояния β ⁻ распада». Physical Review Letters . 69 (15): 2164–2167. Bibcode :1992PhRvL..69.2164J. doi :10.1103/PhysRevLett.69.2164. PMID  10046415.
42. Смоляр, MI; Уокер, RJ; Морган, JW (1996). "Re-Os возрасты железных метеоритов групп IIA, IIIA, IVA и IVB". Science . 271 (5252): 1099–1102. Bibcode :1996Sci...271.1099S. doi :10.1126/science.271.5252.1099. S2CID  96376008.
43. Bosch, F.; et al. (1996). «Наблюдение связанного состояния бета-минус распада полностью ионизированного ¹⁸⁷ Re: ¹⁸⁷ Re– ¹⁸⁷ Os Cosmochronometry». Physical Review Letters . 77 (26): 5190–5193. Bibcode : 1996PhRvL..77.5190B. doi : 10.1103/PhysRevLett.77.5190. PMID  10062738.
44. Bilenky, SM (2010). "Безнейтринный двойной бета-распад". Physics of Particles and Nuclei . 41 (5): 690–715. arXiv : 1001.1946 . Bibcode :2010PPN....41..690B. doi :10.1134/S1063779610050035. hdl :10486/663891. S2CID  55217197.

Библиография

• Томонага, С.-И. (1997). История спина . Издательство Чикагского университета .
• Тули, Дж. К. (2011). Ядерные кошельки (PDF) (8-е изд.). Брукхейвенская национальная лаборатория . Архивировано (PDF) из оригинала 2022-10-09.

Внешние ссылки

• Текущая карта нуклидов - МАГАТЭ с фильтром по типу распада
• Моделирование бета-распада [1]