Эксперимент Штерна–Герлаха

Физический эксперимент 1922 года, демонстрирующий, что атомный спин квантуется

Эксперимент Штерна-Герлаха : атомы серебра, движущиеся через неоднородное магнитное поле и отклоняющиеся вверх или вниз в зависимости от их спина; (1) печь, (2) пучок атомов серебра, (3) неоднородное магнитное поле, (4) классически ожидаемый результат, (5) наблюдаемый результат

В квантовой физике эксперимент Штерна -Герлаха продемонстрировал, что пространственная ориентация углового момента квантуется . Таким образом, было показано , что система атомного масштаба имеет внутренне квантовые свойства. В оригинальном эксперименте атомы серебра были отправлены через пространственно-переменное магнитное поле , которое отклоняло их до того, как они ударялись об экран детектора, такой как стеклянный слайд. Частицы с ненулевым магнитным моментом отклонялись из-за градиента магнитного поля от прямого пути. Экран показал дискретные точки накопления, а не непрерывное распределение, ^[1] из-за их квантованного спина . Исторически этот эксперимент был решающим в убеждении физиков в реальности квантования углового момента во всех системах атомного масштаба. ^{[2] [3] [4]}

После того, как Отто Штерн задумал этот эксперимент в 1921 году, он был впервые успешно проведен Вальтером Герлахом в начале 1922 года. ^{[1] [5] [6]}

Описание

Видео, объясняющее квантовый спин против классического магнита в эксперименте Штерна-Герлаха

Эксперимент Штерна-Герлаха заключается в пропускании атомов серебра через неоднородное магнитное поле и наблюдении за их отклонением. Атомы серебра испарялись с помощью электрической печи в вакууме. С помощью тонких щелей атомы направлялись в плоский пучок, а пучок направлялся через неоднородное магнитное поле перед столкновением с металлической пластиной. Законы классической физики предсказывают, что совокупность конденсированных атомов серебра на пластине должна образовывать тонкую сплошную линию той же формы, что и исходный пучок. Однако неоднородное магнитное поле заставило пучок разделиться в двух отдельных направлениях, создав две линии на металлической пластине.

Результаты показывают, что частицы обладают собственным угловым моментом , который очень похож на угловой момент классически вращающегося объекта, но который принимает только определенные квантованные значения. Другим важным результатом является то, что только один компонент спина частицы может быть измерен в один момент времени, что означает, что измерение спина вдоль оси z уничтожает информацию о спине частицы вдоль осей x и y.

Эксперимент обычно проводится с использованием электрически нейтральных частиц, таких как атомы серебра. Это позволяет избежать большого отклонения на пути заряженной частицы, движущейся через магнитное поле, и позволяет спин-зависимым эффектам доминировать. ^{[7] [8]}

Если частица рассматривается как классический вращающийся магнитный диполь , она будет прецессировать в магнитном поле из-за крутящего момента, который магнитное поле оказывает на диполь (см. прецессия, вызванная крутящим моментом ). Если она движется через однородное магнитное поле, силы, действующие на противоположные концы диполя, компенсируют друг друга, и траектория частицы не изменяется. Однако, если магнитное поле неоднородно, то сила на одном конце диполя будет немного больше, чем противодействующая сила на другом конце, так что существует чистая сила, которая отклоняет траекторию частицы. Если бы частицы были классическими вращающимися объектами, можно было бы ожидать, что распределение векторов их спинового углового момента будет случайным и непрерывным . Каждая частица будет отклоняться на величину, пропорциональную скалярному произведению ее магнитного момента с градиентом внешнего поля, создавая некоторое распределение плотности на экране детектора. Вместо этого частицы, проходящие через аппарат Штерна-Герлаха, отклоняются либо вверх, либо вниз на определенную величину. Это было измерение квантовой наблюдаемой величины , теперь известной как спиновый угловой момент, которое продемонстрировало возможные результаты измерения, где наблюдаемая величина имеет дискретный набор значений или точечный спектр . ^[9]

Хотя некоторые дискретные квантовые явления, такие как атомные спектры , наблюдались гораздо раньше, эксперимент Штерна–Герлаха позволил ученым впервые в истории науки напрямую наблюдать разделение между дискретными квантовыми состояниями.

Теоретически квантовый угловой момент любого вида имеет дискретный спектр , который иногда кратко выражают как «угловой момент квантуется » .

Эксперимент с использованием частиц со спином +1/2 или −1/2

Если эксперимент проводится с использованием заряженных частиц, таких как электроны, то будет существовать сила Лоренца , которая стремится искривить траекторию по окружности. Эту силу можно нейтрализовать электрическим полем соответствующей величины, ориентированным поперек траектории заряженной частицы.

Значения спина для фермионов

Электроны являются частицами со спином 1/2 . Они имеют только два возможных значения спинового углового момента, измеренных вдоль любой оси, или , чисто квантово-механическое явление. Поскольку его значение всегда одинаково, оно рассматривается как внутреннее свойство электронов и иногда известно как «собственный угловой момент» (чтобы отличить его от орбитального углового момента, который может меняться и зависит от присутствия других частиц). Если измерять спин вдоль вертикальной оси, электроны описываются как «спин вверх» или «спин вниз», на основе магнитного момента, направленного вверх или вниз соответственно. ${\displaystyle +{\frac {\hbar }{2}}}$ ${\displaystyle -{\frac {\hbar }{2}}}$

Для математического описания эксперимента со спиновыми частицами проще всего использовать обозначение Дирака . Когда частицы проходят через устройство Штерна– Герлаха , они отклоняются либо вверх, либо вниз и наблюдаются детектором, который решает, вращаться ли им вверх или вниз. Они описываются квантовым числом углового момента , которое может принимать одно из двух возможных разрешенных значений, либо . Акт наблюдения (измерения) импульса вдоль оси соответствует оператору углового момента оси , часто обозначаемому . В математических терминах начальное состояние частиц равно ${\displaystyle +{\frac {1}{2}}}$ ${\displaystyle j}$ ${\displaystyle +{\frac {\hbar }{2}}}$ ${\displaystyle -{\frac {\hbar }{2}}}$ ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle J_{z}}$

${\displaystyle |\psi \rangle =c_{1}\left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle +c_{2}\left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle }$

где константы и являются комплексными числами. Этот начальный спин состояния может указывать в любом направлении. Квадраты абсолютных значений и являются соответственно вероятностями для системы в состоянии , которое будет найдено во время и после измерения вдоль оси. Константы и также должны быть нормализованы для того, чтобы вероятность нахождения любого из значений была равна единице, то есть мы должны гарантировать, что . Однако этой информации недостаточно для определения значений и , поскольку они являются комплексными числами. Поэтому измерение дает только квадраты величин констант, которые интерпретируются как вероятности. ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle |c_{1}|^{2}}$ ${\displaystyle |c_{2}|^{2}}$ ${\displaystyle |\psi \rangle }$ ${\displaystyle \left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle }$ ${\displaystyle \left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle }$ ${\displaystyle z}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle |c_{1}|^{2}+|c_{2}|^{2}=1}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$

Последовательные эксперименты

Если мы свяжем несколько аппаратов Штерна-Герлаха (прямоугольники, содержащие SG ), мы ясно увидим, что они не действуют как простые селекторы, т. е. отфильтровывают частицы с одним из состояний (существовавших до измерения) и блокируют другие. Вместо этого они изменяют состояние, наблюдая за ним (как при поляризации света ). На рисунке ниже x и z обозначают направления (неоднородного) магнитного поля, причем плоскость xz ортогональна пучку частиц. В трех системах SG, показанных ниже, заштрихованные квадраты обозначают блокировку заданного выхода, т. е. каждая из систем SG с блокировщиком позволяет только частицам с одним из двух состояний попадать в следующий аппарат SG в последовательности. ^[10]

Эксп. 1 - Обратите внимание, что на втором анализаторе SG не обнаружено z-нейтронов.

Эксперимент 1

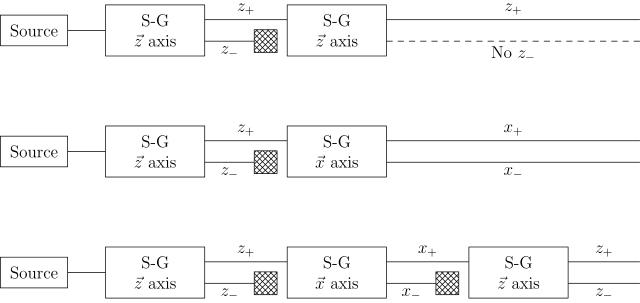
Верхняя иллюстрация показывает, что когда второй, идентичный, аппарат SG помещается на выходе первого аппарата, на выходе второго аппарата виден только z+ . Этот результат ожидаем, поскольку все частицы в этой точке, как ожидается, имеют спин z+, поскольку только луч z+ из первого аппарата вошел во второй аппарат. ^[11]

Эксп. 2 — z-спин известен, теперь измеряем x-спин.

Эксперимент 2

Средняя система показывает, что происходит, когда другой аппарат SG помещается на выходе z+ луча, полученного из первого аппарата, второй аппарат измеряет отклонение лучей по оси x вместо оси z. Второй аппарат выдает x+ и x- выходные сигналы. Теперь классически мы ожидали бы иметь один луч с характеристикой x, ориентированной +, и характеристикой z, ориентированной +, и другой с характеристикой x, ориентированной -, и характеристикой z, ориентированной +. ^[11]

Эксп. 3 — Нейтроны, предположительно имеющие только z+ спин, были измерены снова и обнаружено, что z-спин был «сброшен».

Эксперимент 3

Нижняя система противоречит этому ожиданию. Выход третьего аппарата, который измеряет отклонение по оси z, снова показывает выход z-, а также z+. Учитывая, что вход во второй аппарат SG состоял только из z+ , можно сделать вывод, что аппарат SG должен изменять состояния частиц, которые проходят через него. Этот эксперимент можно интерпретировать как демонстрацию принципа неопределенности : поскольку угловой момент не может быть измерен в двух перпендикулярных направлениях одновременно, измерение углового момента в направлении x разрушает предыдущее определение углового момента в направлении z. Вот почему третий аппарат измеряет обновленные лучи z+ и z-, как измерение x, действительно сделало чистый лист выходного сигнала z+. ^[11]

История

Мемориальная доска в Франкфуртском институте, посвященная эксперименту

Эксперимент Штерна-Герлаха был задуман Отто Штерном в 1921 году и выполнен им и Вальтером Герлахом во Франкфурте в 1922 году. ^[10] Во время эксперимента наиболее распространенной моделью для описания атома была модель Бора-Зоммерфельда , ^{[12] [13]} которая описывала электроны как движущиеся вокруг положительно заряженного ядра только на определенных дискретных атомных орбиталях или уровнях энергии . Поскольку электрон был квантован, чтобы находиться только в определенных положениях в пространстве, разделение на отдельные орбиты называлось пространственным квантованием . Эксперимент Штерна-Герлаха был призван проверить гипотезу Бора-Зоммерфельда о том, что направление углового момента атома серебра квантуется. ^[14]

Эксперимент был впервые проведен с электромагнитом, который позволял постепенно включать неоднородное магнитное поле от нулевого значения. ^[1] Когда поле было нулевым, атомы серебра осаждались в виде одной полосы на стеклянном предметном стекле детектора. Когда поле становилось сильнее, середина полосы начинала расширяться и в конечном итоге разделялась на две, так что изображение на стеклянном предметном стекле выглядело как отпечаток губ с отверстием посередине и закрытием на обоих концах. ^[15] В середине, где магнитное поле было достаточно сильным, чтобы разделить луч на два, статистически половина атомов серебра отклонялась неоднородностью поля.

Обратите внимание, что эксперимент был проведен за несколько лет до того, как Джордж Уленбек и Сэмюэл Гоудсмит сформулировали свою гипотезу о существовании спина электрона в 1925 году. ^[16] Хотя результат эксперимента Штерна-Герлаха позже оказался в соответствии с предсказаниями квантовой механики для частицы со спином 1/2, экспериментальный результат также согласуется с теорией Бора-Зоммерфельда . ^[17]

В 1927 году TE Phipps и JB Taylor воспроизвели эффект, используя атомы водорода в их основном состоянии , тем самым устранив любые сомнения, которые могли быть вызваны использованием атомов серебра . ^[18] Однако в 1926 году нерелятивистское скалярное уравнение Шредингера неверно предсказало, что магнитный момент водорода в его основном состоянии равен нулю. Чтобы исправить эту проблему, Вольфганг Паули рассмотрел версию уравнения Шредингера со спином 1/2, используя 3 матрицы Паули , которые теперь носят его имя, что позже было показано Полем Дираком в 1928 году как следствие его релятивистского уравнения Дирака .

В начале 1930-х годов Штерн вместе с Отто Робертом Фришем и Иммануэлем Эстерманом усовершенствовали аппарат молекулярного пучка в достаточной степени, чтобы измерить магнитный момент протона , величину почти в 2000 раз меньшую, чем момент электрона. В 1931 году теоретический анализ Грегори Брейта и Исидора Исаака Раби показал, что этот аппарат можно использовать для измерения ядерного спина, когда известна электронная конфигурация атома. Эта концепция была применена Раби и Виктором В. Коэном в 1934 году для определения спина атомов натрия . ^[19] ${\displaystyle 3/2}$

В 1938 году Раби и его коллеги вставили элемент осциллирующего магнитного поля в свой аппарат, изобретя ядерно-магнитную резонансную спектроскопию. ^{[20] [21]} Настраивая частоту осциллятора на частоту ядерных прецессий, они могли выборочно настраиваться на каждый квантовый уровень изучаемого материала. За эту работу Раби был удостоен Нобелевской премии в 1944 году. ^[22]

Важность

Эксперимент Штерна–Герлаха был первым прямым доказательством квантования углового момента в квантовой механике ^[23] и оказал сильное влияние на последующие разработки в современной физике :

• В последующее десятилетие ученые показали, используя аналогичные методы, что ядра некоторых атомов также имеют квантованный угловой момент. ^[20] Именно взаимодействие этого ядерного углового момента со спином электрона ответственно за сверхтонкую структуру спектроскопических линий. ^[24]
• Норман Ф. Рэмси позже модифицировал аппарат Раби, чтобы улучшить его чувствительность (используя метод разделенного колебательного поля ). ^[25] В начале шестидесятых годов Рэмси, Х. Марк Голденберг и Дэниел Клеппнер использовали систему Штерна-Герлаха для получения пучка поляризованного водорода в качестве источника энергии для водородного мазера . ^[26] Это привело к разработке чрезвычайно стабильных часов на основе водородного мазера. С 1967 по 2019 год секунда определялась на основе сверхтонкого перехода 9 192 631 770 Гц атома цезия-133 ; атомные часы , которые используются для установки этого стандарта, являются применением работы Рэмси. ^[27]
• Эксперимент Штерна-Герлаха стал прототипом квантового измерения , демонстрируя наблюдение единственного, действительного значения ( собственного значения ) ранее неопределенного физического свойства. ^{[28] [29] [30]} При входе в магнит Штерна-Герлаха направление магнитного момента атома серебра неопределенно, но когда атом регистрируется на экране, он наблюдается либо в одной точке, либо в другой, и этот результат не может быть предсказан заранее. Поскольку эксперимент иллюстрирует характер квантовых измерений, в Фейнмановских лекциях по физике используются идеализированные аппараты Штерна-Герлаха для объяснения базовой математики квантовой теории. ^{[31] [32] [33]}

Смотрите также

• Поляризация фотона
• Медаль Штерна-Герлаха
• Немецкие изобретатели и первооткрыватели

Ссылки

1. Герлах, В.; Стерн, О. (1922). «Der Experimentelle Nachweis der Richtungsquantelung im Magnetfeld» [Экспериментальное доказательство направленного квантования в магнитном поле]. Zeitschrift für Physik . 9 (1): 349–352. Бибкод : 1922ZPhy....9..349G. дои : 10.1007/BF01326983. S2CID  186228677.
2. Франклин, Аллан; Перович, Слободан. «Эксперимент в физике, Приложение 5». В Zalta, Edward N. (ред.). The Stanford Encyclopedia of Philosophy (зима 2016 г.) . Получено 14 августа 2018 г.
3. Фридрих, Б.; Хершбах, Д. (2003). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику». Physics Today . 56 (12): 53. Bibcode : 2003PhT....56l..53F. doi : 10.1063/1.1650229 . S2CID  17572089.
4. Кастельвекки, Д. (2022). «Эксперимент Штерна–Герлаха на отметке 100». Nature Reviews Physics . 4 (3): 140–142. Bibcode : 2022NatRP...4..140C. doi : 10.1038/s42254-022-00436-4. S2CID  247184330.
5. Герлах, В.; Стерн, О. (1922). «Das Magneticische Moment des Silberatoms» [Магнитный момент атома серебра]. Zeitschrift für Physik . 9 (1): 353–355. Бибкод : 1922ZPhy....9..353G. дои : 10.1007/BF01326984. S2CID  126109346.
6. Герлах, В.; Стерн, О. (1922). «Der Experimentelle Nachweis des Magneticischen Moments des Silberatoms» [Экспериментальное доказательство магнитного момента атома серебра]. Zeitschrift für Physik . 8 (1): 110–111. Бибкод : 1922ZPhy....8..110G. дои : 10.1007/BF01329580. S2CID  122648402.
7. Mott, NF , Massey, HSW (1965/1971). Теория атомных столкновений , третье издание, Oxford University Press, Oxford UK, стр. 214–219, §2, гл. IX, перепечатано в Wheeler, JA ; Zurek, WH (1983). Квантовая теория и измерение . Princeton NJ: Princeton University Press. стр. 701–706.
8. Резерфорд, Джордж Х.; Гроуб, Райнер (1997). "Комментарий к "Эффекту Штерна-Герлаха для электронных пучков"". Phys. Rev. Lett . 81 (4772): 4772. Bibcode : 1998PhRvL..81.4772R. doi : 10.1103/PhysRevLett.81.4772.
9. Перес, Эшер (1993). Квантовая теория: концепции и методы . Kluwer . стр. 14–18. ISBN 0-7923-2549-4.
10. Sakurai, J.-J. (1985). Современная квантовая механика . Addison-Wesley . ISBN 0-201-53929-2.
11. Qinxun, Li (8 июня 2020 г.). «Эксперимент Штерна-Герлаха: описания и разработки». Университет науки и технологий Китая : 2–5 . Получено 24 ноября 2020 г.
12. Кастельвекки, Давиде (2020). «Just a moment». Nature Physics . 16 (9): 994. Bibcode : 2020NatPh..16..994C. doi : 10.1038/s41567-020-1022-6. S2CID  225215678.
13. Краг, Хельге (2012). «Теория Бора–Зоммерфельда». Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925. Oxford University Press. С. 140–181. doi :10.1093/acprof:oso/9780199654987.003.0004. ISBN 978-0-19-965498-7.
14. Стерн, О. (1921). «Ein Weg zur Experimentellen Pruefung der Richtungsquantelung im Magnetfeld» [Способ экспериментальной проверки направленного квантования в магнитном поле]. Zeitschrift für Physik . 7 (1): 249–253. Бибкод : 1921ZPhy....7..249S. дои : 10.1007/BF01332793. S2CID  186234469.
15. Френч, А. П. , Тейлор, Э. Ф. (1979). Введение в квантовую физику , Van Nostrand Reinhold, Лондон, ISBN 0-442-30770-5 , стр. 428–442. 
16. Айсберг, Роберт; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Wiley. стр. 277. ISBN 9780471873730.
17. Вайнерт, Ф. (1995). «Неправильная теория — правильный эксперимент: значение экспериментов Штерна–Герлаха». Исследования по истории и философии современной физики . 26B (1): 75–86. Bibcode :1995SHPMP..26...75W. doi :10.1016/1355-2198(95)00002-B.
18. Фиппс, TE; Тейлор, JB (1927). «Магнитный момент атома водорода». Physical Review . 29 (2): 309–320. Bibcode : 1927PhRv...29..309P. doi : 10.1103/PhysRev.29.309.
19. Kellogg, JBM; Millman, S. (1946-07-01). «Метод магнитного резонанса молекулярного пучка. Радиочастотные спектры атомов и молекул». Reviews of Modern Physics . 18 (3): 323–352. doi :10.1103/RevModPhys.18.323. ISSN  0034-6861.
20. Раби, II; Захариас, JR; Миллман, С. и Куш, П. (1938). «Новый метод измерения ядерного магнитного момента». Physical Review . 53 (4): 318–327. Bibcode :1938PhRv...53..318R. doi : 10.1103/PhysRev.53.318 .
21. Гамильтон, Дональд Р. (1941-12-01). «Молекулярные пучки и ядерные моменты». American Journal of Physics . 9 (6): 319–337. doi :10.1119/1.1991712. ISSN  0002-9505.
22. "Нобелевская премия по физике 1944 года". NobelPrize.org .
23. Джонстон, Хэмиш (2022-12-01). «100 лет эксперименту Штерна–Герлаха». Physics World . 35 (12): 27–30. doi :10.1088/2058-7058/35/12/30. ISSN  0953-8585.
24. Гриффитс, Дэвид (2005). Введение в квантовую механику (2-е изд.). Pearson Prentice Hall . стр. 267. ISBN 0-13-111892-7.
25. "Норман Ф. Рэмси – Автобиография". Нобелевский фонд . Получено 13 июня 2013 г.
26. Рэмси, Норман Ф. (1968). «Мазер атомарного водорода». American Scientist . 56 (4): 420–438. ISSN  0003-0996. JSTOR  27828332.
27. "Пресс-релиз Нобелевской премии". Фонд Нобеля . Получено 13 июня 2013 г.
28. Бом, Дэвид (1951). Квантовая теория . Нью-Йорк: Prentice-Hall. С. 326–330.
29. Готфрид, Курт (1966). Квантовая механика . Нью-Йорк: WA Benjamin, Inc., стр. 170–174.
30. Айсберг, Роберт (1961). Основы современной физики . Нью-Йорк: Джон Уайли и сыновья. стр. 334–338. ISBN 0-471-23463-X.
31. Фейнман, Ричард П .; Лейтон, Роберт Б.; Сэндс , Мэтью Л. (2006) [1966]. "5. Spin One". Лекции Фейнмана по физике . Том 3 (Окончательное издание). Сан-Франциско, Калифорния: Pearson Addison Wesley. ISBN 978-0-8053-9045-2.
32. Гейл, В.; Гут, Э.; Траммелл, Г. Т. (1968-01-25). «Определение квантового состояния с помощью измерений». Physical Review . 165 (5): 1434–1436. doi :10.1103/PhysRev.165.1434.
33. Ududec, Cozmin; Barnum, Howard; Emerson, Joseph (март 2011 г.). «Эксперименты с тремя щелями и структура квантовой теории». Foundations of Physics . 41 (3): 396–405. arXiv : 0909.4787 . Bibcode :2011FoPh...41..396U. doi :10.1007/s10701-010-9429-z.

Дальнейшее чтение

• Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). «Динамика Штерна-Герлаха с квантовыми пропагаторами». Physical Review A. 83 ( 1): 012109–1–12. Bibcode : 2011PhRvA..83a2109H. doi : 10.1103/PhysRevA.83.012109.
• Margalit, Yair; Zhou, Zhifan; Machluf, Shimon; Japha, Yonathan; Moukouri, Samuel; Folman, Ron (2019-07-23). ​​"Анализ высокостабильного пространственного интерферометра Штерна–Герлаха". New Journal of Physics . 21 (7): 073040. Bibcode :2019NJPh...21g3040M. doi : 10.1088/1367-2630/ab2fdc .
• Рейниш, Г. (1999). «Эксперимент Штерна–Герлаха как пионер — и, вероятно, самый простой — тест квантовой запутанности?». Physics Letters A. 259 ( 6): 427–430. Bibcode : 1999PhLA..259..427R. doi : 10.1016/S0375-9601(99)00472-7.
• Савицкий, Зак (2023-12-05). «(Часто) упускаемый из виду эксперимент, открывший квантовый мир». Журнал Quanta .
• Венугопалан, А. (1997). «Декогеренция и состояния кота Шредингера в эксперименте типа Штерна–Герлаха». Physical Review A. 56 ( 5): 4307–4310. Bibcode : 1997PhRvA..56.4307V. doi : 10.1103/PhysRevA.56.4307.
• Цвибах, Бартон (2022). «12.2: Эксперимент Штерна-Герлаха». Освоение квантовой механики: основы, теория и приложения . МТИ Пресс. ISBN 978-0-262-04613-8.

Внешние ссылки

• Анимация Java-апплета эксперимента Штерна-Герлаха
• Модель вспышки эксперимента Штерна-Герлаха
• Подробное объяснение эксперимента Штерна-Герлаха
• Анимация, приложения и исследования, связанные со спином (Университет Париж-Юг)
• Волновая механика и эксперимент Штерна-Герлаха в Массачусетском технологическом институте OpenCourseWare