Парадокс Гильберта о Гранд Отеле ( разговорный : Парадокс Бесконечного Отеля или Отель Гильберта ) — это мысленный эксперимент , который иллюстрирует противоречивое свойство бесконечных множеств . Показано, что полностью заполненный отель с бесконечным количеством номеров все же может принять дополнительных гостей, даже бесконечное их количество, и этот процесс может повторяться бесконечно часто. Идея была представлена Давидом Гильбертом в лекции 1925 года «Über das Unendliche», перепечатанной в (Hilbert 2013, стр.730), и была популяризирована в книге Джорджа Гамова 1947 года «Один, два, три... бесконечность ». [1] [2]
Гильберт представляет себе гипотетический отель с номерами 1, 2, 3 и т. д. без верхнего предела. Это называется счетно-бесконечным числом комнат. Первоначально каждая комната занята, но затем приходят новые посетители, каждый из которых ожидает свою комнату. Обычный ограниченный отель не сможет принять новых гостей, если все номера заполнены. Однако можно показать, что существующие гости и вновь прибывшие — даже бесконечное их число — могут иметь каждый свой номер в бесконечном отеле.
С одним дополнительным гостем отель может разместить их и существующих гостей, если бесконечное количество гостей одновременно перемещают номера. Гость, находящийся в данный момент в комнате 1, перемещается в комнату 2, гость, находящийся в данный момент в комнате 2, в комнату 3 и так далее, перемещая каждого гостя из текущей комнаты n в комнату n +1. В бесконечном отеле нет последней комнаты, поэтому у каждого гостя есть комната, куда можно пойти. После этого комната 1 пустует, и в нее можно переселить нового гостя. Повторяя эту процедуру, можно освободить место для любого конечного числа новых гостей. В общем, когда k гостей ищут номер, отель может применить ту же процедуру и переместить каждого гостя из номера n в номер n + k .
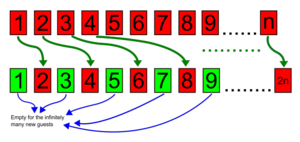
Также возможно разместить счетно-бесконечное число новых гостей: достаточно переместить человека, занимающего комнату 1, в комнату 2, гостя, занимающего комнату 2, в комнату 4 и, вообще, гостя, занимающего комнату n , в комнату 2 n (2 раз n ), и все комнаты с нечетными номерами (которые счетно бесконечны) будут бесплатными для новых гостей.
Можно разместить счетно-бесконечное количество вагонов со счетно-бесконечным числом пассажиров в каждом несколькими различными способами. Большинство методов зависят от того, что места в вагонах уже пронумерованы (или используют аксиому счетного выбора ). В общем , для решения этой проблемы можно использовать любую функцию сопряжения . Для каждого из этих методов предположим, что номер пассажирского места в автобусе равен , а номер его вагона равен , а числа и затем вводятся в два аргумента функции сопряжения .
Отправьте гостя из комнаты в комнату , затем разместите груз первого вагона по комнатам , груз второго вагона по комнатам ; Обычно для номера тренера мы используем номера , в которых есть нечетное простое число . Это решение оставляет некоторые комнаты пустыми (что может быть полезно для отеля, а может и нет); в частности, все числа, не являющиеся простыми степенями , например 15 или 847, больше не будут заняты. (Итак, строго говоря, это показывает, что число прибывших меньше или равно числу созданных вакансий. Легче показать независимыми средствами, что число прибывших также больше или равно числу (Алгоритм работает одинаково хорошо, если поменять местами и , но какой бы выбор ни был сделан, он должен применяться единообразно во всем.)
В номер можно поместить каждого человека с определенным местом и в автобусе (при условии, что c = 0 для людей, уже находящихся в отеле, 1 для первого тренера и т. д.). Поскольку каждое число имеет уникальную простую факторизацию , легко увидеть, что у всех людей будет своя комната, но никакие два человека не окажутся в одной комнате. Например, человек в номере 2592 ( ) сидел в 4-м вагоне на 5-м месте. Как и метод простых степеней, это решение оставляет некоторые комнаты пустыми.
Этот метод также можно легко расширить для бесконечных ночей, бесконечных входов и т. д. ( )
Для каждого пассажира сравните длины и , записанные в любой позиционной системе счисления , например десятичной . (Считайте каждого жителя отеля находящимся в вагоне №0.) Если какое-либо число короче, добавляйте к нему ведущие нули до тех пор, пока оба значения не будут иметь одинаковое количество цифр. Перемешайте цифры, чтобы получить номер зала: его цифры будут такими: [первая цифра номера тренера]-[первая цифра номера места]-[вторая цифра номера тренера]-[вторая цифра номера места] и т. д. Гость отеля (вагон № 0) из номера 1729 переезжает в номер 01070209 (т. е. номер 1 070 209). Пассажир на месте 1234 автобуса 789 проходит в номер 01728394 (т.е. номер 1 728 394).
В отличие от решения Prime Powers, это решение полностью заполняет отель, и мы можем реконструировать исходный вагон и сиденье гостя, обратив процесс чередования. Сначала добавьте ведущий ноль, если в номере нечетное количество цифр. Затем разделите число на два числа: номер вагона состоит из нечетных цифр, а номер места — из четных. Конечно, исходная кодировка произвольна, и роли двух чисел можно поменять местами (четное место и четное место), если оно применяется последовательно.
Те, кто уже находится в отеле, будут переселены в номер треугольного или третьего номера . Те, кто в вагоне , будут находиться в номере или треугольном номере плюс . Таким образом, все комнаты будут заполнены одним и только одним гостем.
Эту функцию сопряжения можно продемонстрировать визуально, структурировав отель в виде бесконечно высокой пирамиды глубиной в одну комнату . Самый верхний ряд пирамиды представляет собой одну комнату: комната 1; второй ряд — помещения 2 и 3; и так далее. Колонка, образованная набором крайних правых комнат, будет соответствовать треугольным числам. После их заполнения (перераспределенными жильцами отеля) оставшиеся пустые комнаты образуют форму пирамиды, точно идентичную первоначальной форме. Таким образом, процесс можно повторить для каждого бесконечного множества. Выполнение этого по одному для каждого тренера потребует бесконечного числа шагов, но, используя предыдущие формулы, гость может определить, какой «будет» его комната, как только в процессе будет достигнут его тренер, и может просто пойти туда. немедленно.
Позволять . счетно, поскольку счетно, следовательно, мы можем перечислить его элементы . Теперь, если , назначьте го гостя го вагона в номер (считайте гостей, уже находящихся в отеле, гостями го вагона). Таким образом, у нас есть функция, распределяющая каждого человека по комнате; кроме того, это задание не пропускает ни одной комнаты.
Предположим, что отель находится рядом с океаном, и к нему прибывает бесконечное количество автомобильных паромов , каждый из которых перевозит бесконечное количество автобусов, каждый с бесконечным числом пассажиров. Это ситуация, включающая три «уровня» бесконечности , и ее можно решить путем расширения любого из предыдущих решений.
Метод простой факторизации можно применить, добавив новое простое число для каждого дополнительного слоя бесконечности ( с паромом).
Решение с использованием простой степени может применяться с дальнейшим возведением простых чисел в степень, что приводит к очень большому количеству комнат даже при небольших входных данных. Например, пассажир на втором сиденье третьего автобуса на втором пароме (адрес 2-3-2) увеличит 2-е нечетное простое число (5) до 49, что является результатом того, что 3-е нечетное простое число (7) будет возведен в степень номера его места (2). Этот номер комнаты будет состоять из более чем тридцати десятичных цифр.
Метод перемежения можно использовать с тремя перемежающимися «нитями» вместо двух. Пассажир с адресом 2-3-2 пойдет в номер 232, а пассажир с адресом 4935-198-82217 - в номер 008,402,912,391,587 (ведущие нули можно удалить).
Предвидя возможность создания любого количества слоев бесконечного количества гостей, отель может пожелать распределить номера таким образом, чтобы ни одному гостю не нужно было переезжать, независимо от того, сколько гостей прибудет впоследствии. Одним из решений является преобразование адреса каждого прибытия в двоичное число , в котором единицы используются в качестве разделителей в начале каждого слоя, а число внутри данного слоя (например, номер тренера гостя) представляется таким же количеством нулей. Таким образом, гость с предыдущим адресом 2-5-1-3-1 (пять бесконечных слоев) перейдет в комнату 10010000010100010 (десятичное число 295458).
В качестве дополнительного шага в этом процессе из каждой части числа можно удалить один ноль; в этом примере новая комната гостя — 101000011001 (десятичное число 2585). Это гарантирует, что каждая комната может быть заполнена гипотетическим гостем. Если не прибудет бесконечное множество гостей, то будут заняты только комнаты, имеющие степень двойки.
Хотя место можно найти для любого конечного числа вложенных бесконечностей людей, то же самое не всегда верно для бесконечного числа слоев. Даже если на каждом слое существует конечное число элементов.
Парадокс Гильберта — это настоящий парадокс : он приводит к противоречивому интуитивному результату, который доказуемо верен. Утверждения «в каждой комнате есть гость» и «гости больше не могут быть размещены» не эквивалентны , когда комнат бесконечно много.
Поначалу такое положение дел может показаться нелогичным. Свойства бесконечных коллекций вещей совершенно отличаются от свойств конечных коллекций вещей. Парадокс Гранд-отеля Гильберта можно понять, используя теорию трансфинитных чисел Кантора . Таким образом, в обычной (конечной) гостинице, имеющей более одного номера, количество нечетных номеров заведомо меньше общего числа номеров. Однако в «Гранд-отеле Гильберта» количество нечетных номеров не меньше общего «числа» номеров. С математической точки зрения мощность подмножества , содержащего комнаты с нечетными номерами, равна мощности множества всех комнат. Действительно, бесконечные множества характеризуются как множества, имеющие собственные подмножества одинаковой мощности. Для счетных множеств (множеств той же мощности, что и натуральные числа ) эта мощность равна . [3]
Перефразируя, для любого счетно-бесконечного множества существует биективная функция, которая отображает счетно-бесконечное множество в множество натуральных чисел, даже если счетно-бесконечное множество содержит натуральные числа. Например, набор рациональных чисел — тех чисел, которые можно записать как частное целых чисел — содержит натуральные числа в качестве подмножества, но не больше, чем набор натуральных чисел, поскольку рациональные числа счетны: существует биекция из естественное к рациональному.