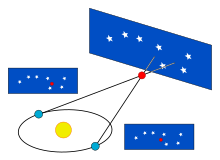
Наиболее важные фундаментальные измерения расстояний в астрономии происходят из тригонометрического параллакса , применяемого в методе звездного параллакса . По мере того, как Земля вращается вокруг Солнца, положение близлежащих звезд будет казаться слегка смещенным относительно более удаленного фона. Эти смещения представляют собой углы в равнобедренном треугольнике , где 2 а.е. (расстояние между крайними положениями орбиты Земли вокруг Солнца) составляют основание треугольника, а расстояние до звезды — длинные равные по длине стороны. Величина смещения довольно мала, даже для ближайших звезд, составляя 1 угловую секунду для объекта на расстоянии 1 парсека (3,26 светового года ), а затем уменьшается в угловой величине по мере увеличения расстояния. Астрономы обычно выражают расстояния в единицах парсеков (параллаксных угловых секунд); в популярных средствах массовой информации используются световые годы.
Поскольку параллакс становится меньше с увеличением расстояния до звезды, полезные расстояния могут быть измерены только для звезд, которые находятся достаточно близко, чтобы иметь параллакс, превышающий точность измерения более чем в несколько раз. Например, в 1990-х годах миссия Hipparcos получила параллаксы для более чем сотни тысяч звезд с точностью около миллисекунды дуги , [1] предоставляя полезные расстояния для звезд до нескольких сотен парсеков. Широкоугольная камера 3 космического телескопа Хаббл имеет потенциал для обеспечения точности от 20 до 40 микросекунд дуги, что позволяет проводить надежные измерения расстояний до 5000 парсеков (16000 световых лет) для небольшого количества звезд. [2] [3] Космическая миссия Gaia предоставила аналогичные точные расстояния для большинства звезд ярче 15-й величины. [4]
Расстояния можно измерить в пределах 10% до Галактического центра , примерно в 30 000 световых лет. Звезды имеют скорость относительно Солнца, которая вызывает собственное движение (поперечное по небу) и радиальную скорость (движение к Солнцу или от Солнца). Первая определяется путем построения графика изменения положения звезд в течение многих лет, в то время как последняя получается путем измерения доплеровского смещения спектра звезды, вызванного движением вдоль луча зрения. Для группы звезд с одинаковым спектральным классом и схожим диапазоном звездных величин средний параллакс может быть выведен из статистического анализа собственных движений относительно их радиальных скоростей. Этот статистический метод параллакса полезен для измерения расстояний ярких звезд за пределами 50 парсек и гигантских переменных звезд , включая цефеиды и переменные звезды типа RR Лиры . [5]


Движение Солнца в пространстве обеспечивает более длинную базовую линию, которая увеличит точность измерений параллакса, известного как вековой параллакс . Для звезд в диске Млечного Пути это соответствует средней базовой линии в 4 а.е. в год, в то время как для звезд гало базовая линия составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на порядки больше базовой линии Земля-Солнце, используемой для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость наблюдаемых звезд является дополнительной неизвестной. При применении к выборкам из нескольких звезд неопределенность может быть уменьшена; неопределенность обратно пропорциональна квадратному корню размера выборки. [8]
Движущийся параллакс скопления — это метод, при котором движения отдельных звезд в соседнем звездном скоплении могут быть использованы для определения расстояния до скопления. Только рассеянные скопления находятся достаточно близко, чтобы этот метод был полезен. В частности, расстояние, полученное для Гиад, исторически было важным шагом в лестнице расстояний.
Для других отдельных объектов могут быть сделаны фундаментальные оценки расстояния при особых обстоятельствах. Если расширение газового облака, например остатка сверхновой или планетарной туманности , можно наблюдать с течением времени, то можно оценить расстояние параллакса расширения до этого облака. Однако эти измерения страдают от неопределенностей в отклонении объекта от сферичности. Расстояние до двойных звезд , которые являются как визуальными , так и спектроскопическими двойными, также можно оценить аналогичными способами, и они не страдают от вышеуказанной геометрической неопределенности. Общей характеристикой этих методов является то, что измерение углового движения сочетается с измерением абсолютной скорости (обычно получаемой с помощью эффекта Доплера ). Оценка расстояния происходит из вычисления того, насколько далеко должен находиться объект, чтобы его наблюдаемая абсолютная скорость отображалась вместе с наблюдаемым угловым движением.
В частности, параллаксы расширения могут дать фундаментальные оценки расстояний для очень далеких объектов, поскольку выбросы сверхновых имеют большие скорости расширения и большие размеры (по сравнению со звездами). Кроме того, их можно наблюдать с помощью радиоинтерферометров , которые могут измерять очень малые угловые движения. Они объединяются, чтобы дать фундаментальные оценки расстояний до сверхновых в других галактиках. [9] Хотя такие случаи и ценны, они довольно редки, поэтому они служат важными проверками согласованности на лестнице расстояний, а не рабочими лошадками сами по себе.

Парсек (символ: пк) — единица длины, используемая для измерения больших расстояний до астрономических объектов за пределами Солнечной системы , приблизительно равная 3,26 световым годам или 206 265 астрономическим единицам (а.е.), то есть 30,9 триллиона километров (19,2 триллиона миль ). [a] Единица парсек получается с помощью параллакса и тригонометрии и определяется как расстояние, на котором 1 а.е. стягивает угол в одну угловую секунду [10] ( 1/3600 градуса ). Ближайшая звезда, Проксима Центавра , находится примерно в 1,3 парсека (4,2 световых года) от Солнца : с этого расстояния расстояние между Землей и Солнцем составляет чуть меньше 1/3600 одного градуса зрения. [11] Большинство звезд, видимых невооруженным глазом, находятся в пределах нескольких сотен парсеков от Солнца, самые далекие — в нескольких тысячах парсеков, а галактика Андромеды — более чем в 700 000 парсеков. [12]
Слово парсек является портманто от «параллакс одной секунды» и было придумано британским астрономом Гербертом Холлом Тернером в 1913 году [13] для упрощения астрономических расчетов астрономических расстояний только на основе необработанных данных наблюдений. Отчасти по этой причине эта единица является предпочтительной в астрономии и астрофизике , хотя световой год остается важной в научно-популярных текстах и обычном использовании. Хотя парсеки используются для более коротких расстояний в пределах Млечного Пути , для более крупных масштабов во Вселенной требуются кратные парсекам, включая килопарсеки (кпк) для более удаленных объектов внутри и вокруг Млечного Пути, мегапарсеки (Мпк) для галактик среднего расстояния и гигапарсеки (Гпк) для многих квазаров и самых далеких галактик.
В августе 2015 года Международный астрономический союз (МАС) принял Резолюцию B2, в которой в рамках определения стандартизированной шкалы абсолютной и кажущейся болометрической величины упоминалось существующее явное определение парсека как именно 648 000/π au, или приблизительно3,085 677 581 491 3673 × 10 16 метров (на основе определения астрономической единицы МАС 2012 года). Это соответствует малоугловому определению парсека, встречающемуся во многих астрономических справочниках. [14] [15]
Звездный параллакс, созданный относительным движением между Землей и звездой , можно рассматривать в модели Коперника как возникающий из орбиты Земли вокруг Солнца: звезда только кажется движущейся относительно более удаленных объектов на небе. В геостатической модели движение звезды должно было бы считаться реальным , поскольку звезда колеблется по небу относительно фоновых звезд.
Звездный параллакс чаще всего измеряется с помощью годового параллакса , определяемого как разница в положении звезды, видимой с Земли и Солнца, т. е. угол, образуемый звездой средним радиусом орбиты Земли вокруг Солнца. Парсек ( 3,26 световых года ) определяется как расстояние, для которого годовой параллакс составляет 1 угловую секунду . Годовой параллакс обычно измеряется путем наблюдения за положением звезды в разное время года по мере движения Земли по своей орбите. Измерение годового параллакса было первым надежным способом определения расстояний до ближайших звезд. Первые успешные измерения звездного параллакса были выполнены Фридрихом Бесселем в 1838 году для звезды 61 Лебедя с помощью гелиометра . [16] Звездный параллакс остается стандартом для калибровки других методов измерения. Точные расчеты расстояния на основе звездного параллакса требуют измерения расстояния от Земли до Солнца, которое теперь основано на отражении радиолокационного сигнала от поверхностей планет. [17]
Углы, используемые в этих расчетах, очень малы и поэтому их трудно измерить. Ближайшая к Солнцу звезда (и, следовательно, звезда с самым большим параллаксом), Проксима Центавра , имеет параллакс 0,7687 ± 0,0003 угловых секунд. [18] Этот угол приблизительно равен углу, образуемому объектом диаметром 2 сантиметра, находящимся на расстоянии 5,3 километра.

Тот факт, что звездный параллакс был настолько мал, что в то время его невозможно было наблюдать , использовался в качестве главного научного аргумента против гелиоцентризма в раннюю современную эпоху. Из геометрии Евклида ясно , что эффект был бы необнаружим, если бы звезды находились достаточно далеко, но по разным причинам такие гигантские расстояния казались совершенно неправдоподобными: одним из главных возражений Тихо против гелиоцентризма Коперника было то, что для того, чтобы он был совместим с отсутствием наблюдаемого звездного параллакса, между орбитой Сатурна (тогда самой далекой известной планеты) и восьмой сферой (неподвижными звездами) должна была бы быть огромная и маловероятная пустота . [20]
В 1989 году спутник Hipparcos был запущен в первую очередь для получения улучшенных параллаксов и собственных движений для более чем 100 000 близлежащих звезд, что увеличило охват метода в десять раз. Тем не менее, Hipparcos смог измерить углы параллакса только для звезд на расстоянии до примерно 1600 световых лет , что составляет чуть больше одного процента от диаметра Галактики Млечный Путь . Миссия Gaia Европейского космического агентства , запущенная в декабре 2013 года, может измерять углы параллакса с точностью до 10 микросекунд дуги , таким образом, отображая близлежащие звезды (и потенциально планеты) на расстоянии до десятков тысяч световых лет от Земли. [21] [22] В апреле 2014 года астрономы НАСА сообщили, что космический телескоп Хаббл , используя пространственное сканирование, может точно измерять расстояния до 10 000 световых лет, что является десятикратным улучшением по сравнению с более ранними измерениями. [19]
Суточный параллакс — это параллакс, который меняется в зависимости от вращения Земли или разницы в местоположении на Земле. Луна и в меньшей степени планеты земной группы или астероиды, видимые с разных точек наблюдения на Земле (в один и тот же момент), могут выглядеть по-разному расположенными на фоне неподвижных звезд. [23] [24]
Суточный параллакс был использован Джоном Флемстидом в 1672 году для измерения расстояния до Марса в его противостоянии и с помощью этого для оценки астрономической единицы и размера Солнечной системы . [25]
Лунный параллакс (часто сокращенно от лунного горизонтального параллакса или лунного экваториального горизонтального параллакса ) является частным случаем (суточного) параллакса: Луна, будучи ближайшим небесным телом, имеет самый большой максимальный параллакс среди всех небесных тел, временами превышающий 1 градус. [26]
Диаграмма для звездного параллакса может также иллюстрировать лунный параллакс, если взять диаграмму в уменьшенном масштабе и слегка изменить. Вместо «ближняя звезда» читать «Луна», и вместо того, чтобы считать круг внизу диаграммы представляющим размер орбиты Земли вокруг Солнца, возьмите его за размер земного шара и окружность вокруг поверхности Земли. Тогда лунный (горизонтальный) параллакс равен разнице в угловом положении Луны относительно фона далеких звезд, как видно из двух разных точек наблюдения на Земле.
Одна из позиций наблюдения — это место, с которого Луна видна прямо над головой в данный момент. То есть, вид вдоль вертикальной линии на диаграмме. Другая позиция наблюдения — это место, с которого Луна видна на горизонте в тот же момент. То есть, вид вдоль одной из диагональных линий, с позиции на поверхности Земли, примерно соответствующей одной из синих точек на модифицированной диаграмме.
Лунный (горизонтальный) параллакс можно альтернативно определить как угол, образуемый радиусом Земли на расстоянии от Луны [27] [28] — равный углу p на диаграмме, уменьшенному и измененному, как указано выше.
Лунный горизонтальный параллакс в любой момент времени зависит от линейного расстояния Луны от Земли. Линейное расстояние Земля-Луна непрерывно меняется, поскольку Луна следует своей возмущенной и приблизительно эллиптической орбите вокруг Земли. Диапазон изменения линейного расстояния составляет от примерно 56 до 63,7 радиусов Земли, что соответствует горизонтальному параллаксу около градуса дуги, но варьируется от примерно 61,4' до примерно 54'. [26] Астрономический альманах и подобные издания табулируют лунный горизонтальный параллакс и/или линейное расстояние Луны от Земли на периодической, например, ежедневной основе для удобства астрономов (и небесных навигаторов), и изучение того, как эта координата меняется со временем, является частью лунной теории .

Параллакс также можно использовать для определения расстояния до Луны .
Один из способов определения лунного параллакса из одного местоположения — использование лунного затмения. Полная тень Земли на Луне имеет видимый радиус кривизны, равный разнице между видимыми радиусами Земли и Солнца, видимыми с Луны. Этот радиус можно увидеть равным 0,75 градуса, из чего (при видимом радиусе Солнца 0,25 градуса) мы получаем видимый радиус Земли 1 градус. Это дает для расстояния Земля-Луна 60,27 радиусов Земли или 384 399 километров (238 854 миль). Эта процедура была впервые использована Аристархом Самосским [29] и Гиппархом , а позже нашла свое отражение в работе Птолемея . [30]
Диаграмма справа показывает, как возникает ежедневный лунный параллакс в геоцентрической и геостатической планетарной модели, в которой Земля находится в центре планетной системы и не вращается. Она также иллюстрирует важный момент, что параллакс не обязательно должен быть вызван каким-либо движением наблюдателя, вопреки некоторым определениям параллакса, которые говорят, что это так, но может возникать исключительно из-за движения наблюдаемого.
Другой метод — сделать два снимка Луны одновременно из двух мест на Земле и сравнить положения Луны относительно звезд. Используя ориентацию Земли, эти два измерения положения и расстояние между двумя местами на Земле, можно триангулировать расстояние до Луны:

Именно этот метод упоминает Жюль Верн в своем романе 1865 года «С Земли на Луну» :
До тех пор многие люди не имели ни малейшего представления о том, как можно вычислить расстояние, отделяющее Луну от Земли. Это обстоятельство было использовано, чтобы научить их тому, что это расстояние было получено путем измерения параллакса Луны. Если слово «параллакс» казалось им удивительным, им говорили, что это угол, образованный двумя прямыми линиями, идущими от обоих концов радиуса Земли к Луне. Если у них возникали сомнения относительно совершенства этого метода, им немедленно показывали, что не только это среднее расстояние составляло целых двести тридцать четыре тысячи триста сорок семь миль (94 330 лиг), но и что астрономы не ошиблись более чем на семьдесят миль (≈ 30 лиг).
После того, как Коперник предложил свою гелиоцентрическую систему , в которой Земля вращается вокруг Солнца, стало возможным построить модель всей Солнечной системы без масштаба. Чтобы определить масштаб, необходимо измерить только одно расстояние в пределах Солнечной системы, например, среднее расстояние от Земли до Солнца (теперь называемое астрономической единицей , или а.е.). При нахождении с помощью триангуляции это называется солнечным параллаксом , разницей в положении Солнца, наблюдаемом из центра Земли и точки, находящейся на расстоянии одного радиуса Земли, т.е. углом, образуемым на Солнце средним радиусом Земли. Знание солнечного параллакса и среднего радиуса Земли позволяет вычислить а.е., первый, небольшой шаг на долгом пути установления размера и возраста расширения [31] видимой Вселенной.
Примитивный способ определения расстояния до Солнца через расстояние до Луны был предложен еще Аристархом Самосским в его книге «О размерах и расстояниях Солнца и Луны» . Он отметил, что Солнце, Луна и Земля образуют прямоугольный треугольник (с прямым углом у Луны) в момент первой или последней четверти Луны . Затем он подсчитал, что угол Луна-Земля-Солнце составляет 87°. Используя правильную геометрию , но неточные данные наблюдений, Аристарх пришел к выводу, что Солнце находится немного менее чем в 20 раз дальше Луны. Истинное значение этого угла близко к 89° 50', а Солнце находится примерно в 390 раз дальше. [29]
Аристарх указал, что Луна и Солнце имеют почти равные видимые угловые размеры , и поэтому их диаметры должны быть пропорциональны их расстоянию от Земли. Таким образом, он пришел к выводу, что Солнце примерно в 20 раз больше Луны. Этот вывод, хотя и неверный, логически вытекает из его неверных данных. Он предполагает, что Солнце больше Земли, что можно было бы принять в поддержку гелиоцентрической модели. [32]

Хотя результаты Аристарха были неверными из-за ошибок наблюдений, они основывались на правильных геометрических принципах параллакса и стали основой для оценок размера Солнечной системы на протяжении почти 2000 лет, пока транзит Венеры не был правильно замечен в 1761 и 1769 годах. [29] Этот метод был предложен Эдмондом Галлеем в 1716 году, хотя он не дожил до результатов. Использование транзитов Венеры оказалось менее успешным, чем ожидалось, из-за эффекта черной капли , но полученная оценка, 153 миллиона километров, всего на 2% выше ныне принятого значения, 149,6 миллиона километров.
Гораздо позже Солнечная система была «масштабирована» с использованием параллакса астероидов , некоторые из которых, такие как Эрос , проходят гораздо ближе к Земле, чем Венера. В благоприятном противостоянии Эрос может приближаться к Земле на расстояние в 22 миллиона километров. [33] Во время противостояния 1900–1901 годов была запущена всемирная программа по проведению измерений параллакса Эроса для определения солнечного параллакса [34] (или расстояния до Солнца), результаты которой были опубликованы в 1910 году Артуром Хинксом из Кембриджа [35] и Чарльзом Д. Перрином из Ликской обсерватории Калифорнийского университета . [36]
Перрин опубликовал отчеты о ходе работ в 1906 [37] и 1908 годах. [38] Он сделал 965 фотографий с помощью рефлектора Кроссли и выбрал 525 для измерений. [39] Подобная программа была затем выполнена во время более близкого сближения в 1930–1931 годах Гарольдом Спенсером Джонсом . [40] Значение астрономической единицы (примерно расстояние от Земли до Солнца), полученное в ходе этой программы, считалось окончательным до 1968 года, когда радиолокационные и динамические методы параллакса начали производить более точные измерения.
Также радиолокационные отражения, как от Венеры (1958), так и от астероидов, таких как Икар , использовались для определения солнечного параллакса. Сегодня использование телеметрических каналов космических аппаратов решило эту старую проблему. В настоящее время принятое значение солнечного параллакса составляет8,794 143 угловых секунд. [41]
Открытое звездное скопление Гиады в Тельце простирается на такую большую часть неба, 20 градусов, что собственные движения, полученные из астрометрии, по-видимому, сходятся с некоторой точностью к перспективной точке к северу от Ориона. Объединение наблюдаемого видимого (углового) собственного движения в секундах дуги с также наблюдаемым истинным (абсолютным) удаляющимся движением, засвидетельствованным доплеровским красным смещением звездных спектральных линий, позволяет оценить расстояние до скопления (151 световой год) и его звезд-членов во многом таким же образом, как и с использованием годового параллакса. [42]
Динамический параллакс иногда также использовался для определения расстояния до сверхновой, когда оптический волновой фронт вспышки распространяется через окружающие пылевые облака с кажущейся угловой скоростью, в то время как его истинная скорость распространения, как известно, равна скорости света . [43]
Из усовершенствованных релятивистских систем позиционирования был разработан пространственно-временной параллакс , обобщающий обычное понятие параллакса только в пространстве. Затем поля событий в пространстве-времени могут быть выведены напрямую без промежуточных моделей искривления света массивными телами, например, такими, которые используются в формализме PPN . [44]
Два связанных метода могут определять средние расстояния до звезд путем моделирования движения звезд. Оба называются статистическими параллаксами, или по отдельности называются вековыми параллаксами и классическими статистическими параллаксами.
Движение Солнца в пространстве обеспечивает более длинную базовую линию, которая увеличит точность измерений параллакса, известного как вековой параллакс . Для звезд в диске Млечного Пути это соответствует средней базовой линии в 4 а.е. в год. Для звезд гало базовая линия составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на порядки больше базовой линии Земля-Солнце, используемой для традиционного параллакса. Вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость других звезд является дополнительной неизвестной. При применении к выборкам из нескольких звезд неопределенность может быть уменьшена; точность обратно пропорциональна квадратному корню размера выборки. [8]
Средние параллаксы и расстояния большой группы звезд можно оценить по их лучевым скоростям и собственным движениям . Это известно как классический статистический параллакс . Движения звезд моделируются для статистического воспроизведения дисперсии скоростей на основе их расстояния. [8] [45]
В астрономии термин «параллакс» стал обозначать метод оценки расстояний, не обязательно использующий истинный параллакс, например:
[
абзац 14, страница 342
] Принимая за единицу расстояния R* то, что соответствует параллаксу 1″·0 [… Сноска:]
* Для этой единицы расстояния необходимо название. Г-н
Шарлье
предложил
Siriometer
, но если можно проигнорировать насилие над греческим языком,
можно было бы принять слово
Astron . Профессор
Тернер
предлагает
Parsec
, что можно принять как сокращенную форму «расстояния, соответствующего параллаксу в одну секунду».
Некоторые полагают, что его расчет относительных размеров Земли и Солнца привел Аристарха к выводу, что более логично, что Земля движется вокруг гораздо большего Солнца, чем наоборот.