Мгновенное расстояние Земля-Луна , или расстояние до Луны , это расстояние от центра Земли до центра Луны . Лунное расстояние ( LD или ), или характерное расстояние Земля-Луна , является единицей измерения в астрономии . Более технически, это большая полуось геоцентрической лунной орбиты . Лунное расстояние в среднем составляет приблизительно 385 000 км (239 000 миль), или 1,28 световых секунд ; это примерно в 30 раз больше диаметра Земли или в 9,5 раз больше окружности Земли . Около 389 лунных расстояний составляют астрономическую единицу AU (примерно расстояние от Земли до Солнца).
Расстояние до Луны обычно используется для выражения расстояния до объектов, сближающихся с Землей . [1] Большая полуось Луны является важным астрономическим показателем; точность измерений дальности в несколько миллиметров позволяет определить большую полуось с точностью до нескольких дециметров; это имеет значение для проверки гравитационных теорий, таких как общая теория относительности , [2] и для уточнения других астрономических величин, таких как масса , [3] радиус , [4] и вращение Земли. [5] Измерение также полезно для характеристики радиуса Луны , а также массы и расстояния до Солнца .
Миллиметровые измерения расстояния до Луны производятся путем измерения времени, необходимого лазерному лучу для прохождения пути между станциями на Земле и ретрорефлекторами , размещенными на Луне. Луна удаляется от Земли по спирали со средней скоростью 3,8 см (1,5 дюйма) в год, как было обнаружено в ходе эксперимента по лазерной локации Луны . [6] [7] [8]

Из-за влияния Солнца и других возмущений Луна не движется по истинному эллипсу вокруг Земли. Тем не менее, для определения большой полуоси использовались различные методы . Эрнест Уильям Браун предоставил формулу для параллакса Луны, если смотреть с противоположных сторон Земли, включающую тригонометрические члены. Это эквивалентно формуле для обратной величины расстояния, и среднее значение этого является обратной величиной 384 399 км (238 854 миль). [9] [10] С другой стороны, усредненное по времени расстояние (а не обратная величина среднего обратного расстояния) между центрами Земли и Луны составляет 385 000,6 км (239 228,3 миль). Можно также моделировать орбиту как эллипс, который постоянно меняется, и в этом случае можно найти формулу для большой полуоси, снова включающую тригонометрические члены. Среднее значение по этому методу составляет 383 397 км. [11]
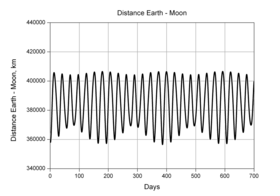
Фактическое расстояние меняется в течение орбиты Луны . Значения при самом близком сближении ( перигей ) или самом дальнем ( апогей ) встречаются тем реже, чем они экстремальнее. График справа показывает распределение перигея и апогея за шесть тысяч лет.
Жан Меус приводит следующие крайние значения для периода с 1500 г. до н.э. по 8000 г. н.э.: [12]

Мгновенное расстояние до Луны постоянно меняется. Фактическое расстояние между Луной и Землей может меняться так же быстро, как75 метров в секунду , [20] или более 1000 км (620 миль) всего за 6 часов, из-за его некруговой орбиты. [21] Есть и другие эффекты, которые также влияют на расстояние до Луны. Некоторые факторы включают:

Формула Шапрона и Тузе для расстояния в километрах начинается с членов: [9]
где - средняя аномалия (более или менее, насколько Луна отошла от перигея) и - средняя элонгация (более или менее, насколько она отошла от соединения с Солнцем в новолуние). Их можно рассчитать из
Г М = 134,963 411 38° + 13,064 992 953 630°/d · t
D = 297,850 204 20° + 12,190 749 117 502°/d · t
где t — время (в днях) с 1 января 2000 года (см. Эпоха (астрономия) ). Это показывает, что наименьший перигей происходит либо в новолуние, либо в полнолуние (около 356870 км), как и наибольший апогей (около 406079 км), тогда как наибольший перигей будет около полумесяца (около 370180 км), как и наименьший апогей (около 404593 км). Точные значения будут немного отличаться из-за других условий. Дважды в каждом цикле полнолуния продолжительностью около 411 дней будет минимальный перигей и максимальный апогей, разделенные двумя неделями, и максимальный перигей и минимальный апогей, также разделенные двумя неделями.
Расстояние до Луны можно измерить с точностью до2 мм за 1-часовой период выборки, [22] что приводит к общей неопределенности в дециметр для большой полуоси. Однако из-за эллиптической орбиты с изменяющимся эксцентриситетом мгновенное расстояние меняется с ежемесячной периодичностью. Кроме того, расстояние возмущено гравитационными эффектами различных астрономических тел – наиболее существенно Солнца и в меньшей степени Венеры и Юпитера. Другие силы, ответственные за мельчайшие возмущения, это: гравитационное притяжение к другим планетам Солнечной системы и к астероидам; приливные силы; и релятивистские эффекты. [23] [24] Эффект давления излучения от Солнца вносит вклад в величину ±3,6 мм до лунного расстояния. [22]
Хотя мгновенная неопределенность составляет несколько миллиметров, измеренное расстояние до Луны может измениться более чем на 30 000 км (19 000 миль) от среднего значения в течение типичного месяца. Эти возмущения хорошо изучены [25] , и расстояние до Луны можно точно смоделировать на протяжении тысяч лет. [23]

Под действием приливных сил момент импульса вращения Земли медленно передается на орбиту Луны. [26] В результате скорость вращения Земли постепенно уменьшается (со скоростью2,4 миллисекунды/столетие ), [27] [28] [29] [30] и лунная орбита постепенно расширяется. Скорость рецессии составляет3,830 ± 0,008 см в год . [25] [28] Однако считается, что эта скорость недавно увеличилась, так как скорость3,8 см/год означало бы, что Луне всего 1,5 миллиарда лет, тогда как научный консенсус поддерживает возраст около 4 миллиардов лет. [31] Также считается, что эта аномально высокая скорость рецессии может продолжать ускоряться. [32]
Теоретически, расстояние до Луны будет продолжать увеличиваться до тех пор, пока Земля и Луна не станут приливно заблокированными , как Плутон и Харон . Это произойдет, когда продолжительность лунного орбитального периода сравняется с периодом вращения Земли, который оценивается в 47 земных дней. Затем два тела будут находиться в равновесии, и дальнейший обмен энергией вращения не будет происходить. Однако модели предсказывают, что для достижения этой конфигурации потребуется 50 миллиардов лет, [33] что значительно больше ожидаемого срока службы Солнечной системы .
Лазерные измерения показывают, что среднее расстояние до Луны увеличивается, что подразумевает, что Луна была ближе в прошлом, и что дни на Земле были короче. Исследования ископаемых раковин моллюсков из кампанской эры (80 миллионов лет назад) показывают, что в то время было 372 дня (по 23 ч 33 мин) в году, что подразумевает, что расстояние до Луны составляло около 60,05 R 🜨 (383 000 км или 238 000 миль). [26] Существуют геологические свидетельства того, что среднее расстояние до Луны составляло около 52 R 🜨 (332 000 км или 205 000 миль) в докембрийский период ; 2500 миллионов лет назад . [31]
Широко принятая гипотеза гигантского удара утверждает, что Луна образовалась в результате катастрофического столкновения Земли с другой планетой, что привело к повторному накоплению фрагментов на начальном расстоянии 3,8 R 🜨 (24 000 км или 15 000 миль). [34] Эта теория предполагает, что первоначальное столкновение произошло 4,5 миллиарда лет назад. [35]
До конца 1950-х годов все измерения расстояния до Луны основывались на оптических угловых измерениях: самое раннее точное измерение было сделано Гиппархом во 2 веке до н. э. Космическая эра ознаменовала поворотный момент, когда точность этого значения значительно улучшилась. В 1950-х и 1960-х годах проводились эксперименты с использованием радаров, лазеров и космических аппаратов, которые проводились с использованием компьютерной обработки и моделирования. [36]
Некоторые исторически значимые или иным образом интересные методы определения расстояния до Луны:
Самый старый метод определения лунного расстояния включал измерение угла между Луной и выбранной точкой отсчета из нескольких мест одновременно. Синхронизация может быть скоординирована путем проведения измерений в заранее определенное время или во время события, которое наблюдалось всеми сторонами. До появления точных механических хронометров событием синхронизации обычно было лунное затмение или момент, когда Луна пересекала меридиан (если наблюдатели находились на одной и той же долготе). Этот метод измерения известен как лунный параллакс .
Для повышения точности измеренный угол можно скорректировать с учетом преломления и искажения света, проходящего через атмосферу.
Ранние попытки измерить расстояние до Луны использовали наблюдения лунного затмения в сочетании со знанием радиуса Земли и пониманием того, что Солнце находится намного дальше Луны. Наблюдая геометрию лунного затмения, расстояние до Луны можно рассчитать с помощью тригонометрии .
Самые ранние сообщения о попытках измерить расстояние до Луны с помощью этого метода были сделаны греческим астрономом и математиком Аристархом Самосским в IV веке до нашей эры [37], а позднее Гиппархом , чьи вычисления дали результат 59–67 R 🜨 (376 000 –427 000 км или233 000 –265 000 миль ). [38] Этот метод позже нашел свое применение в работе Птолемея , [39] который получил результат 64+1 ⁄ 6 Р 🜨 (409 000 км или253 000 миль ) в самой дальней точке. [40]
Экспедиция французского астронома ACD Crommelin наблюдала прохождение лунного меридиана в одну и ту же ночь из двух разных мест. Тщательные измерения с 1905 по 1910 год измеряли угол возвышения в момент, когда определенный лунный кратер ( Mösting A ) пересекал местный меридиан, со станций в Гринвиче и на мысе Доброй Надежды . [41] Расстояние было рассчитано с погрешностью30 км , и это значение оставалось окончательным значением расстояния до Луны на протяжении следующих полувека.
Регистрируя момент, когда Луна закрывает фоновую звезду (или, аналогичным образом, измеряя угол между Луной и фоновой звездой в заранее определенный момент), можно определить расстояние до Луны, если измерения проводятся из нескольких мест с известным расстоянием.
Астрономы О'Киф и Андерсон вычислили расстояние до Луны, наблюдая четыре покрытия из девяти мест в 1952 году. [42] Они вычислили большую полуось384 407 .6 ± 4.7 км (238,859.8 ± 2.9 миль). Это значение было уточнено в 1962 году Ирен Фишер , которая включила обновленные геодезические данные, чтобы получить значение384 403,7 ± 2 км (238 857,4 ± 1 миля). [4]

Расстояние до Луны было впервые измерено с помощью радара в 1946 году в рамках проекта «Диана» . [44]
Позже, в 1957 году, в Военно-морской исследовательской лаборатории США был проведен эксперимент, в котором эхо-сигналы радара использовались для определения расстояния от Земли до Луны. Радарные импульсы длительностью2 мкс транслировались с радиотарелки диаметром 50 футов (15 м). После того, как радиоволны отражались от поверхности Луны, обратный сигнал был обнаружен и время задержки было измерено. Из этого измерения можно было рассчитать расстояние. Однако на практике отношение сигнал/шум было настолько низким, что точное измерение не могло быть надежно произведено. [45]
Эксперимент был повторен в 1958 году в Королевском радиолокационном центре в Англии. Радарные импульсы длительностью5 мкс передавались с пиковой мощностью 2 мегаватта при частоте повторения 260 импульсов в секунду. После того, как радиоволны отразились от поверхности Луны, был обнаружен обратный сигнал и измерено время задержки. Несколько сигналов были сложены вместе для получения надежного сигнала путем наложения осциллограмм на фотопленку. Из измерений расстояние было рассчитано с погрешностью 1,25 км (0,777 мили). [46]
Эти первоначальные эксперименты были предназначены для проверки концепции и длились всего один день. Последующие эксперименты, длившиеся один месяц, дали большую полуось384 402 ± 1,2 км (238 856 ± 0,75 миль) [47] , что было самым точным измерением расстояния до Луны на тот момент.

Эксперимент, в котором измерялось время прохождения лазерных импульсов в оба конца, отраженных непосредственно от поверхности Луны, был проведен в 1962 году группой ученых из Массачусетского технологического института и советской группой в Крымской астрофизической обсерватории . [48]
Во время миссий Аполлон в 1969 году астронавты разместили ретрорефлекторы на поверхности Луны с целью улучшения точности и достоверности этой техники. Измерения продолжаются и включают в себя несколько лазерных установок. Мгновенная точность экспериментов по лазерной локации Луны может достигать небольшого миллиметрового разрешения и является наиболее надежным методом определения расстояния до Луны. Большая полуось определена как 384 399,0 км. [10]
Благодаря современной доступности точных приборов измерения времени, цифровых камер с высоким разрешением, GPS- приемников, мощных компьютеров и практически мгновенной связи астрономы-любители получили возможность проводить высокоточные измерения расстояния до Луны.
23 мая 2007 года были сделаны цифровые фотографии Луны во время почти полного покрытия Регула из двух мест, в Греции и Англии. Путем измерения параллакса между Луной и выбранной фоновой звездой было рассчитано расстояние до Луны. [49]
Более амбициозный проект под названием «Кампания Аристарха» был реализован во время лунного затмения 15 апреля 2014 года . [21] Во время этого мероприятия участникам было предложено сделать серию из пяти цифровых фотографий от восхода Луны до кульминации (точки наибольшей высоты).
Метод использовал тот факт, что Луна на самом деле находится ближе всего к наблюдателю, когда она находится в своей самой высокой точке на небе, по сравнению с тем, когда она находится на горизонте. Хотя кажется, что Луна больше, когда она находится около горизонта, на самом деле все наоборот. Это явление известно как иллюзия Луны . Причина разницы в расстоянии заключается в том, что расстояние от центра Луны до центра Земли почти постоянно в течение ночи, но наблюдатель на поверхности Земли на самом деле находится на расстоянии 1 радиуса Земли от центра Земли. Это смещение приближает их к Луне, когда она находится над головой.
Современные камеры достигли разрешения, способного запечатлеть Луну с достаточной точностью, чтобы обнаружить и измерить это крошечное изменение видимого размера. Результаты этого эксперимента были рассчитаны как LD =60,51+3,91
−4,19 R 🜨 . Принятое значение для той ночи составило 60,61 R 🜨 , что подразумевало точность 3%. Преимущество этого метода в том, что единственным необходимым измерительным оборудованием является современная цифровая камера (оснащенная точными часами и GPS-приемником).
Другие экспериментальные методы измерения расстояния до Луны, которые могут быть использованы астрономами-любителями, включают:
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )