

В математическом моделировании переобучение — это «производство анализа, который слишком близко или точно соответствует определенному набору данных и, следовательно, может не соответствовать дополнительным данным или надежно предсказывать будущие наблюдения». [1] Переобученна модель — это математическая модель , которая содержит больше параметров , чем может быть обосновано данными. [2] В математическом смысле эти параметры представляют степень полинома . Суть переобучения заключается в неосознанном извлечении некоторой остаточной вариации (т. е. шума ), как если бы эта вариация представляла собой базовую структуру модели. [3] : 45
Недообучение происходит, когда математическая модель не может адекватно охватить базовую структуру данных. Недообучение модели — это модель, в которой отсутствуют некоторые параметры или термины, которые могли бы появиться в правильно определенной модели. [2] Недообучение может произойти, например, при подгонке линейной модели к нелинейным данным. Такая модель, как правило, будет иметь плохую предсказательную эффективность.
Возможность переобучения существует, поскольку критерий, используемый для выбора модели , не совпадает с критерием, используемым для оценки пригодности модели. Например, модель может быть выбрана путем максимизации ее производительности на некотором наборе обучающих данных , и все же ее пригодность может определяться ее способностью хорошо работать на невидимых данных; переобучение происходит, когда модель начинает «запоминать» обучающие данные, а не «учиться» обобщать из тенденции.
В качестве крайнего примера, если количество параметров равно или больше количества наблюдений, то модель может идеально предсказать обучающие данные, просто запомнив данные целиком. (Для иллюстрации см. Рисунок 2.) Однако такая модель, как правило, будет давать серьезные сбои при составлении прогнозов.
Переобучение напрямую связано с ошибкой аппроксимации выбранного класса функций и ошибкой оптимизации процедуры оптимизации. Класс функций, который слишком велик, в подходящем смысле, относительно размера набора данных, скорее всего, будет переобучен. [4] Даже если подобранная модель не имеет чрезмерного количества параметров, следует ожидать, что подобранное отношение будет работать хуже на новом наборе данных, чем на наборе данных, использованном для подгонки (явление, иногда называемое усадкой ). [2] В частности, значение коэффициента детерминации уменьшится относительно исходных данных.
Чтобы уменьшить вероятность или объем переобучения, доступны несколько методов (например, сравнение моделей , перекрестная проверка , регуляризация , ранняя остановка , обрезка , байесовские априорные данные или исключение ). Основой некоторых методов является либо (1) явное наказание за слишком сложные модели, либо (2) проверка способности модели к обобщению путем оценки ее производительности на наборе данных, не используемых для обучения, который, как предполагается, аппроксимирует типичные невидимые данные, с которыми столкнется модель.
В статистике вывод делается на основе статистической модели , которая была выбрана с помощью некоторой процедуры. Бернхэм и Андерсон в своем часто цитируемом тексте по выбору модели утверждают, что для того, чтобы избежать переобучения, мы должны придерживаться « Принципа бережливости ». [3] Авторы также утверждают следующее. [3] : 32–33
Переобученные модели... часто свободны от смещения в оценках параметров, но имеют оцененные (и фактические) дисперсии выборки, которые неоправданно велики (точность оценок плохая по сравнению с тем, чего можно было бы достичь с помощью более экономной модели). Ложные эффекты обработки, как правило, выявляются, и ложные переменные включаются в переобученные модели. ... Наилучшая аппроксимирующая модель достигается путем надлежащего балансирования ошибок недообучения и переобучения.
Переобучение, скорее всего, станет серьезной проблемой, когда мало теории, которая могла бы направлять анализ, отчасти потому, что тогда, как правило, есть большое количество моделей, из которых можно выбирать. В книге « Выбор модели и усреднение модели» (2008) это описывается следующим образом. [5]
Имея набор данных, вы можете подогнать тысячи моделей одним нажатием кнопки, но как выбрать лучшую? При таком количестве моделей-кандидатов переобучение становится реальной опасностью. Является ли обезьяна, которая напечатала Гамлета, на самом деле хорошим писателем?
В регрессионном анализе часто происходит переобучение. [6] В качестве крайнего примера, если в линейной регрессии с p точками данных есть p переменных , подобранная линия может точно проходить через каждую точку. [7] Для логистической регрессии или моделей пропорциональных рисков Кокса существует множество эмпирических правил (например, 5–9, [8] 10 [9] и 10–15 [10] — правило 10 наблюдений на независимую переменную известно как « правило одного из десяти »). В процессе выбора регрессионной модели среднеквадратическая ошибка случайной функции регрессии может быть разделена на случайный шум, смещение аппроксимации и дисперсию в оценке функции регрессии. Компромисс между смещением и дисперсией часто используется для преодоления моделей переобучения.
При большом наборе объясняющих переменных , которые на самом деле не имеют никакого отношения к предсказываемой зависимой переменной , некоторые переменные в целом будут ложно признаны статистически значимыми , и исследователь может таким образом сохранить их в модели, тем самым переобучив модель. Это известно как парадокс Фридмана .
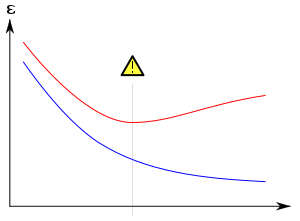
Обычно обучающий алгоритм обучается с использованием некоторого набора «обучающих данных»: образцовых ситуаций, для которых известен желаемый результат. Цель состоит в том, чтобы алгоритм также хорошо предсказывал результат при подаче «проверочных данных», которые не встречались во время его обучения.
Переобучение — это использование моделей или процедур, которые нарушают бритву Оккама , например, путем включения большего количества регулируемых параметров, чем в конечном итоге оптимально, или путем использования более сложного подхода, чем в конечном итоге оптимально. В качестве примера, когда имеется слишком много регулируемых параметров, рассмотрим набор данных, где обучающие данные для y могут быть адекватно предсказаны линейной функцией двух независимых переменных. Такая функция требует только трех параметров (свободного члена и двух наклонов). Замена этой простой функции новой, более сложной квадратичной функцией или новой, более сложной линейной функцией более чем двух независимых переменных несет в себе риск: бритва Оккама подразумевает, что любая заданная сложная функция априори менее вероятна, чем любая заданная простая функция. Если вместо простой функции выбрана новая, более сложная функция, и если не было достаточно большого прироста в обучающих данных, чтобы компенсировать увеличение сложности, то новая сложная функция «переобучает» данные, и сложная переобучаемая функция, вероятно, будет работать хуже, чем более простая функция на проверочных данных за пределами обучающего набора данных, даже если сложная функция работала так же хорошо, или, возможно, даже лучше, на обучающем наборе данных. [11]
При сравнении различных типов моделей сложность нельзя измерить только подсчетом количества параметров в каждой модели; необходимо также учитывать экспрессивность каждого параметра. Например, нетривиально напрямую сравнивать сложность нейронной сети (которая может отслеживать криволинейные отношения) с m параметрами с регрессионной моделью с n параметрами. [11]
Переобучение особенно вероятно в случаях, когда обучение выполнялось слишком долго или когда обучающие примеры редки, заставляя обучающегося подстраиваться под очень специфические случайные особенности обучающих данных, которые не имеют причинно-следственной связи с целевой функцией . В этом процессе переобучения производительность на обучающих примерах все еще увеличивается, в то время как производительность на невидимых данных ухудшается.
В качестве простого примера рассмотрим базу данных розничных покупок, которая включает купленный товар, покупателя, дату и время покупки. Легко построить модель, которая будет идеально соответствовать обучающему набору, используя дату и время покупки для прогнозирования других атрибутов, но эта модель вообще не будет обобщаться на новые данные, потому что эти прошлые разы больше никогда не произойдут.
Обычно говорят, что обучающийся алгоритм переобучен относительно более простого, если он точнее подгоняет известные данные (ретроспективно), но менее точен в прогнозировании новых данных (предвидение). Интуитивно переобучение можно понять из того факта, что информацию из всего прошлого опыта можно разделить на две группы: информацию, которая имеет отношение к будущему, и нерелевантную информацию («шум»). При прочих равных условиях, чем сложнее предсказать критерий (т. е. чем выше его неопределенность), тем больше шума в прошлой информации, который нужно игнорировать. Проблема заключается в определении того, какую часть игнорировать. Обучающийся алгоритм, который может снизить риск подгонки шума, называется « надежным ».
Наиболее очевидным последствием переобучения является плохая производительность на наборе данных проверки. Другие негативные последствия включают:
Оптимальная функция обычно требует проверки на больших или совершенно новых наборах данных. Однако существуют методы, такие как минимальное остовное дерево или время жизни корреляции , которые применяют зависимость между коэффициентами корреляции и временным рядом (шириной окна). Всякий раз, когда ширина окна достаточно велика, коэффициенты корреляции стабильны и больше не зависят от размера ширины окна. Поэтому матрицу корреляции можно создать, вычислив коэффициент корреляции между исследуемыми переменными. Эту матрицу можно представить топологически как сложную сеть, в которой визуализируются прямые и косвенные влияния между переменными.
Регуляризация исключения (случайное удаление данных обучающего набора) также может повысить надежность и, следовательно, снизить переобучение за счет вероятностного удаления входных данных из слоя.

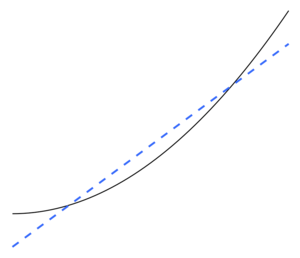
Недообучение — это обратная сторона переобучения, то есть статистическая модель или алгоритм машинного обучения слишком упрощены, чтобы точно улавливать закономерности в данных. Признаком недообучения является то, что в текущей используемой модели или алгоритме обнаружены высокое смещение и низкая дисперсия (обратная сторона переобучения: низкое смещение и высокая дисперсия ). Это можно понять из компромисса смещения-дисперсии , который является методом анализа модели или алгоритма на предмет ошибки смещения, ошибки дисперсии и неустранимой ошибки. При высоком смещении и низкой дисперсии результатом модели является то, что она будет неточно представлять точки данных и, таким образом, недостаточно способна предсказывать будущие результаты данных (см. Ошибка обобщения ). Как показано на рисунке 5, линейная линия не может представлять все заданные точки данных из-за того, что линия не напоминает кривизну точек. Мы ожидали бы увидеть линию в форме параболы, как показано на рисунках 6 и 1. Если бы мы использовали рисунок 5 для анализа, мы получили бы ложные прогностические результаты, противоречащие результатам, полученным при анализе рисунка 6.
Бернхэм и Андерсон утверждают следующее. [3] : 32
... недообученная модель будет игнорировать некоторые важные воспроизводимые (т. е. концептуально воспроизводимые в большинстве других образцов) структуры в данных и, таким образом, не сможет идентифицировать эффекты, которые фактически поддерживаются данными. В этом случае смещение в оценках параметров часто бывает существенным, а дисперсия выборки недооценивается, оба фактора приводят к плохому охвату доверительного интервала. Недообученные модели, как правило, упускают важные эффекты лечения в экспериментальных условиях.
Существует несколько способов борьбы с недообучением:
Доброкачественное переобучение описывает явление статистической модели, которая, по-видимому, хорошо обобщает невидимые данные, даже когда она идеально подходит для зашумленных обучающих данных (т. е. достигает идеальной точности предсказания на обучающем наборе). Это явление представляет особый интерес для глубоких нейронных сетей , но изучается с теоретической точки зрения в контексте гораздо более простых моделей, таких как линейная регрессия . В частности, было показано, что сверхпараметризация имеет важное значение для доброкачественного переобучения в этой обстановке. Другими словами, количество направлений в пространстве параметров, которые не важны для прогнозирования, должно значительно превышать размер выборки. [16]