Функция плотности вероятности

Понятие в математике

Диаграмма ящиков и функция плотности вероятности нормального распределения N (0,  σ ² ) .

Геометрическая визуализация моды , медианы и среднего значения произвольной унимодальной функции плотности вероятности. ^[1]

В теории вероятностей функция плотности вероятности ( PDF ), функция плотности или плотность абсолютно непрерывной случайной величины — это функция, значение которой в любой заданной выборке (или точке) в пространстве выборок (множестве возможных значений, принимаемых случайной величиной) можно интерпретировать как предоставление относительной вероятности того, что значение случайной величины будет равно этому образцу. ^{[2] [3]} Плотность вероятности — это вероятность на единицу длины, другими словами, в то время как абсолютная вероятность того, что непрерывная случайная величина примет какое-либо конкретное значение, равна 0 (поскольку изначально существует бесконечный набор возможных значений), значение PDF в двух различных выборках можно использовать для того, чтобы сделать вывод, при любом конкретном извлечении случайной величины, насколько более вероятно, что случайная величина будет близка к одному образцу по сравнению с другим образцом.

Точнее, PDF используется для указания вероятности попадания случайной величины в определенный диапазон значений , а не принятия какого-либо одного значения. Эта вероятность задается интегралом PDF этой переменной по этому диапазону, то есть она задается площадью под функцией плотности, но выше горизонтальной оси и между наименьшим и наибольшим значениями диапазона. Функция плотности вероятности везде неотрицательна, а площадь под всей кривой равна 1.

Термины функция распределения вероятностей и функция вероятности также иногда использовались для обозначения функции плотности вероятности. Однако такое использование не является стандартным среди вероятностников и статистиков. В других источниках «функция распределения вероятностей» может использоваться, когда распределение вероятностей определяется как функция над общими наборами значений или может относиться к кумулятивной функции распределения , или это может быть функция массы вероятности (PMF), а не плотность. Сама «функция плотности» также используется для функции массы вероятности, что приводит к дальнейшей путанице. ^[4] Однако, в общем, PMF используется в контексте дискретных случайных величин (случайных величин, которые принимают значения на счетном множестве), в то время как PDF используется в контексте непрерывных случайных величин.

Пример

Примеры четырех непрерывных функций плотности вероятности.

Предположим, что бактерии определенного вида обычно живут от 20 до 30 часов. Вероятность того, что бактерия проживет ровно 5 часов, равна нулю. Многие бактерии живут примерно 5 часов, но нет никаких шансов, что любая данная бактерия умрет ровно через 5,00... часов. Однако вероятность того, что бактерия умрет между 5 часами и 5,01 часами, поддается количественной оценке. Предположим, что ответ равен 0,02 (т. е. 2%). Тогда вероятность того, что бактерия умрет между 5 часами и 5,001 часами, должна быть около 0,002, поскольку этот временной интервал в десять раз короче предыдущего. Вероятность того, что бактерия умрет между 5 часами и 5,0001 часами, должна быть около 0,0002 и так далее.

В этом примере отношение (вероятность жизни в течение интервала) / (продолжительность интервала) приблизительно постоянно и равно 2 в час (или 2 часа ⁻¹ ). Например, существует вероятность 0,02 умереть в интервале 0,01 часа между 5 и 5,01 часами, и (вероятность 0,02 / 0,01 часа) = 2 часа ⁻¹ . Эта величина 2 часа ⁻¹ называется плотностью вероятности умереть около 5 часов. Следовательно, вероятность того, что бактерия умрет через 5 часов, можно записать как (2 часа ⁻¹ ) dt . Это вероятность того, что бактерия умрет в течение бесконечно малого промежутка времени около 5 часов, где dt — продолжительность этого окна. Например, вероятность того, что он проживет дольше 5 часов, но короче (5 часов + 1 наносекунда), составляет (2 часа ⁻¹ )×(1 наносекунда) ≈6 × 10 ⁻¹³ (используя преобразование единиц 3,6 × 10 ¹² наносекунд = 1 час).

Существует функция плотности вероятности f с f (5 часов) = 2 часа ⁻¹ . Интеграл f по любому временному интервалу (не только бесконечно малым , но и большим) — это вероятность того, что бактерия погибнет в этом интервале.

Абсолютно непрерывные одномерные распределения

Функция плотности вероятности чаще всего ассоциируется с абсолютно непрерывными одномерными распределениями . Случайная величина имеет плотность , где — неотрицательная функция , интегрируемая по Лебегу , если: ${\displaystyle X}$ ${\displaystyle f_{X}}$ ${\displaystyle f_{X}}$ $${\displaystyle \Pr[a\leq X\leq b]=\int _{a}^{b}f_{X}(x)\,dx.}$$

Следовательно, если — кумулятивная функция распределения , то: и (если — непрерывна при ) ${\displaystyle F_{X}}$ ${\displaystyle X}$ $${\displaystyle F_{X}(x)=\int _{-\infty }^{x}f_{X}(u)\,du,}$$ ${\displaystyle f_{X}}$ ${\displaystyle x}$ $${\displaystyle f_{X}(x)={\frac {d}{dx}}F_{X}(x).}$$

Интуитивно можно представить себе как вероятность попадания в бесконечно малый интервал . ${\displaystyle f_{X}(x)\,dx}$ ${\displaystyle X}$ ${\displaystyle [x,x+dx]}$

Формальное определение

( Это определение можно распространить на любое распределение вероятностей, используя определение вероятности с точки зрения теории меры . )

Случайная величина со значениями в измеримом пространстве (обычно с борелевскими множествами в качестве измеримых подмножеств) имеет в качестве распределения вероятностей меру прямого распространения X _∗ P на : плотность относительно эталонной меры на является производной Радона–Никодима : ${\displaystyle X}$ ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ ${\displaystyle X}$ ${\displaystyle \mu }$ ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ $${\displaystyle f={\frac {dX_{*}P}{d\mu }}.}$$

То есть f — это любая измеримая функция со следующим свойством: для любого измеримого множества $${\displaystyle \Pr[X\in A]=\int _{X^{-1}A}\,dP=\int _{A}f\,d\mu }$$ ${\displaystyle A\in {\mathcal {A}}.}$

Обсуждение

В непрерывном одномерном случае выше, эталонной мерой является мера Лебега . Функция массы вероятности дискретной случайной величины является плотностью относительно меры подсчета по выборочному пространству (обычно множеству целых чисел или некоторому его подмножеству).

Невозможно определить плотность относительно произвольной меры (например, нельзя выбрать счетную меру в качестве точки отсчета для непрерывной случайной величины). Более того, когда она существует, плотность почти уникальна, что означает, что любые две такие плотности совпадают почти всюду .

Дополнительные подробности

В отличие от вероятности, функция плотности вероятности может принимать значения больше единицы; например, непрерывное равномерное распределение на интервале [0, 1/2] имеет плотность вероятности f ( x ) = 2 для 0 ≤ x ≤ 1/2 и f ( x ) = 0 в остальных местах.

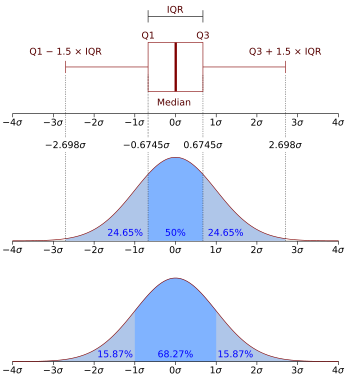
Стандартное нормальное распределение имеет плотность вероятности $${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\,e^{-x^{2}/2}.}$$

Если дана случайная величина X и ее распределение допускает функцию плотности вероятности f, то ожидаемое значение X ( если ожидаемое значение существует ) можно вычислить как $${\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\,f(x)\,dx.}$$

Не каждое распределение вероятностей имеет функцию плотности: распределения дискретных случайных величин ее не имеют; ее нет и у распределения Кантора , хотя оно и не имеет дискретного компонента, т. е. не присваивает положительную вероятность какой-либо отдельной точке.

Распределение имеет функцию плотности тогда и только тогда, когда его кумулятивная функция распределения F ( x ) абсолютно непрерывна . В этом случае: F почти всюду дифференцируема , и ее производная может быть использована как плотность вероятности: $${\displaystyle {\frac {d}{dx}}F(x)=f(x).}$$

Если распределение вероятностей допускает плотность, то вероятность каждого одноточечного множества { a } равна нулю; то же самое справедливо для конечных и счетных множеств.

Две плотности вероятности f и g представляют одно и то же распределение вероятностей , если они отличаются только на множестве нулевой меры Лебега .

В области статистической физики неформальная переформулировка приведенного выше соотношения между производной кумулятивной функции распределения и функцией плотности вероятности обычно используется в качестве определения функции плотности вероятности. Это альтернативное определение следующее:

Если dt — бесконечно малое число, то вероятность того, что X попадет в интервал ( t , t + dt ) , равна f ( t ) dt , или: $${\displaystyle \Pr(t<X<t+dt)=f(t)\,dt.}$$

Связь между дискретным и непрерывным распределениями

Можно представить некоторые дискретные случайные величины, а также случайные величины, включающие как непрерывную, так и дискретную часть, с помощью обобщенной функции плотности вероятности, используя дельта-функцию Дирака . (Это невозможно с функцией плотности вероятности в определенном выше смысле, это можно сделать с помощью распределения .) Например, рассмотрим двоичную дискретную случайную величину, имеющую распределение Радемахера — то есть принимающую −1 или 1 для значений, с вероятностью 1 ⁄ 2 каждое. Плотность вероятности, связанная с этой переменной, равна: $${\displaystyle f(t)={\frac {1}{2}}(\delta (t+1)+\delta (t-1)).}$$

В более общем случае, если дискретная переменная может принимать n различных значений среди действительных чисел, то соответствующая функция плотности вероятности имеет вид: где — дискретные значения, доступные переменной, и — вероятности, связанные с этими значениями. $${\displaystyle f(t)=\sum _{i=1}^{n}p_{i}\,\delta (t-x_{i}),}$$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle p_{1},\ldots ,p_{n}}$

Это существенно унифицирует обработку дискретных и непрерывных распределений вероятностей. Вышеприведенное выражение позволяет определять статистические характеристики такой дискретной переменной (такие как среднее значение , дисперсия и эксцесс ), исходя из формул, приведенных для непрерывного распределения вероятности.

Семейства плотностей

Обычно функции плотности вероятности (и функции массы вероятности ) параметризуются, то есть характеризуются неопределенными параметрами . Например, нормальное распределение параметризуется в терминах среднего значения и дисперсии , обозначаемых и соответственно, что дает семейство плотностей Различные значения параметров описывают различные распределения различных случайных величин на одном и том же выборочном пространстве (один и тот же набор всех возможных значений переменной); это выборочное пространство является областью семейства случайных величин, которые описывает это семейство распределений. Данный набор параметров описывает единственное распределение в пределах семейства, разделяющее функциональную форму плотности. С точки зрения данного распределения параметры являются константами, а члены в функции плотности, которые содержат только параметры, но не переменные, являются частью нормировочного фактора распределения (мультипликативный фактор, который гарантирует, что область под плотностью — вероятность того, что что-то произойдет в области — равна 1). Этот нормировочный фактор находится вне ядра распределения. ${\displaystyle \mu }$ ${\displaystyle \sigma ^{2}}$ $${\displaystyle f(x;\mu ,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}.}$$

Поскольку параметры являются константами, перепараметризация плотности в терминах других параметров для характеристики другой случайной величины в семействе означает простую подстановку новых значений параметров в формулу вместо старых.

Плотности, связанные с несколькими переменными

Для непрерывных случайных величин X ₁ , ..., X _n также можно определить функцию плотности вероятности, связанную с набором в целом, часто называемую совместной функцией плотности вероятности . Эта функция плотности определяется как функция n переменных, такая, что для любой области D в n -мерном пространстве значений переменных X ₁ , ..., X _n вероятность того, что реализация множества переменных попадет в область D, равна $${\displaystyle \Pr \left(X_{1},\ldots ,X_{n}\in D\right)=\int _{D}f_{X_{1},\ldots ,X_{n}}(x_{1},\ldots ,x_{n})\,dx_{1}\cdots dx_{n}.}$$

Если F ( x ₁ , ..., x _n ) = Pr( X ₁ ≤ x ₁ , ..., X _n ≤ x _n ) — кумулятивная функция распределения вектора ( X ₁ , ..., X _n ) , то совместная функция плотности вероятности может быть вычислена как частная производная $${\displaystyle f(x)=\left.{\frac {\partial ^{n}F}{\partial x_{1}\cdots \partial x_{n}}}\right|_{x}}$$

Предельные плотности

Для i = 1, 2, ..., n пусть f _{X i} ( x _i ) будет функцией плотности вероятности, связанной только с переменной X _i . Это называется функцией предельной плотности и может быть выведено из плотности вероятности, связанной со случайными величинами X ₁ , ..., X _{n ,} путем интегрирования по всем значениям других n − 1 переменных: $${\displaystyle f_{X_{i}}(x_{i})=\int f(x_{1},\ldots ,x_{n})\,dx_{1}\cdots dx_{i-1}\,dx_{i+1}\cdots dx_{n}.}$$

Независимость

Непрерывные случайные величины X ₁ , ..., X _{n ,} допускающие совместную плотность, независимы друг от друга тогда и только тогда, когда $${\displaystyle f_{X_{1},\ldots ,X_{n}}(x_{1},\ldots ,x_{n})=f_{X_{1}}(x_{1})\cdots f_{X_{n}}(x_{n}).}$$

Следствие

Если совместную функцию плотности вероятности вектора из n случайных величин можно разложить на произведение n функций одной переменной (где каждая f _i не обязательно является плотностью), то все n переменных в наборе независимы друг от друга, а предельная функция плотности вероятности каждой из них определяется выражением $${\displaystyle f_{X_{1},\ldots ,X_{n}}(x_{1},\ldots ,x_{n})=f_{1}(x_{1})\cdots f_{n}(x_{n}),}$$ $${\displaystyle f_{X_{i}}(x_{i})={\frac {f_{i}(x_{i})}{\int f_{i}(x)\,dx}}.}$$

Пример

Этот элементарный пример иллюстрирует приведенное выше определение многомерных функций плотности вероятности в простом случае функции набора двух переменных. Назовем двумерный случайный вектор координат ( X , Y ) : вероятность получить в четверти плоскости положительные x и y равна ${\displaystyle {\vec {R}}}$ ${\displaystyle {\vec {R}}}$ $${\displaystyle \Pr \left(X>0,Y>0\right)=\int _{0}^{\infty }\int _{0}^{\infty }f_{X,Y}(x,y)\,dx\,dy.}$$

Функция случайных величин и изменение переменных в функции плотности вероятности

Если функция плотности вероятности случайной величины (или вектора) X задана как f _X ( x ) , то можно (но часто не обязательно; см. ниже) вычислить функцию плотности вероятности некоторой переменной Y = g ( X ) . Это также называется «заменой переменной» и на практике используется для генерации случайной величины произвольной формы f _{g ( X )} = f _Y с использованием известного (например, равномерного) генератора случайных чисел.

Возникает соблазн думать, что для того, чтобы найти ожидаемое значение E( g ( X )) , нужно сначала найти плотность вероятности f _{g ( X )} новой случайной величины Y = g ( X ) . Однако вместо вычисления можно найти $${\displaystyle \operatorname {E} {\big (}g(X){\big )}=\int _{-\infty }^{\infty }yf_{g(X)}(y)\,dy,}$$ $${\displaystyle \operatorname {E} {\big (}g(X){\big )}=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx.}$$

Значения двух интегралов одинаковы во всех случаях, когда и X , и g ( X ) фактически имеют функции плотности вероятности. Не обязательно, чтобы g была функцией один к одному . В некоторых случаях последний интеграл вычисляется гораздо проще, чем первый. См. Закон бессознательного статистика .

Скаляр в скаляр

Пусть будет монотонной функцией , тогда результирующая функция плотности равна ^[5] ${\displaystyle g:\mathbb {R} \to \mathbb {R} }$ $${\displaystyle f_{Y}(y)=f_{X}{\big (}g^{-1}(y){\big )}\left|{\frac {d}{dy}}{\big (}g^{-1}(y){\big )}\right|.}$$

Здесь g ⁻¹ обозначает обратную функцию .

Это следует из того факта, что вероятность, содержащаяся в дифференциальной области, должна быть инвариантной относительно замены переменных. То есть, или $${\displaystyle \left|f_{Y}(y)\,dy\right|=\left|f_{X}(x)\,dx\right|,}$$ $${\displaystyle f_{Y}(y)=\left|{\frac {dx}{dy}}\right|f_{X}(x)=\left|{\frac {d}{dy}}(x)\right|f_{X}(x)=\left|{\frac {d}{dy}}{\big (}g^{-1}(y){\big )}\right|f_{X}{\big (}g^{-1}(y){\big )}={\left|\left(g^{-1}\right)'(y)\right|}\cdot f_{X}{\big (}g^{-1}(y){\big )}.}$$

Для функций, которые не являются монотонными, функция плотности вероятности для y равна , где n ( y ) — число решений относительно x для уравнения , а — эти решения. $${\displaystyle \sum _{k=1}^{n(y)}\left|{\frac {d}{dy}}g_{k}^{-1}(y)\right|\cdot f_{X}{\big (}g_{k}^{-1}(y){\big )},}$$ ${\displaystyle g(x)=y}$ ${\displaystyle g_{k}^{-1}(y)}$

Вектор в вектор

Предположим, что _x — n - мерная случайная величина с совместной плотностью f . Если y = G ( x ) , где G — биективная , дифференцируемая функция , то y имеет плотность pY : с дифференциалом, рассматриваемым как якобиан обратной функции G (⋅) , вычисленной в y . ^[6] $${\displaystyle p_{Y}(\mathbf {y} )=f{\Bigl (}G^{-1}(\mathbf {y} ){\Bigr )}\left|\det \left[\left.{\frac {dG^{-1}(\mathbf {z} )}{d\mathbf {z} }}\right|_{\mathbf {z} =\mathbf {y} }\right]\right|}$$

Например, в 2-мерном случае x = ( x ₁ , x ₂ ) , предположим, что преобразование G задано как y ₁ = G ₁ ( x ₁ , x ₂ ) , y ₂ = G ₂ ( x ₁ , x ₂ ) с обратными x ₁ = G ₁ ⁻¹ ( y ₁ , y ₂ ) , x ₂ = G ₂ ⁻¹ ( y ₁ , y ₂ ) . Совместное распределение для y  = ( y ₁ , y ₂ ) имеет плотность ^[7] $${\displaystyle p_{Y_{1},Y_{2}}(y_{1},y_{2})=f_{X_{1},X_{2}}{\big (}G_{1}^{-1}(y_{1},y_{2}),G_{2}^{-1}(y_{1},y_{2}){\big )}\left\vert {\frac {\partial G_{1}^{-1}}{\partial y_{1}}}{\frac {\partial G_{2}^{-1}}{\partial y_{2}}}-{\frac {\partial G_{1}^{-1}}{\partial y_{2}}}{\frac {\partial G_{2}^{-1}}{\partial y_{1}}}\right\vert .}$$

Вектор в скаляр

Пусть будет дифференцируемой функцией и будет случайным вектором, принимающим значения в , будет функцией плотности вероятности и будет дельта-функцией Дирака . Можно использовать приведенные выше формулы для определения , функции плотности вероятности , которая будет задана как ${\displaystyle V:\mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle X}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle f_{X}}$ ${\displaystyle X}$ ${\displaystyle \delta (\cdot )}$ ${\displaystyle f_{Y}}$ ${\displaystyle Y=V(X)}$ $${\displaystyle f_{Y}(y)=\int _{\mathbb {R} ^{n}}f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,d\mathbf {x} .}$$

Этот результат приводит к закону бессознательного статистика : $${\displaystyle \operatorname {E} _{Y}[Y]=\int _{\mathbb {R} }yf_{Y}(y)\,dy=\int _{\mathbb {R} }y\int _{\mathbb {R} ^{n}}f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,d\mathbf {x} \,dy=\int _{{\mathbb {R} }^{n}}\int _{\mathbb {R} }yf_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,dy\,d\mathbf {x} =\int _{\mathbb {R} ^{n}}V(\mathbf {x} )f_{X}(\mathbf {x} )\,d\mathbf {x} =\operatorname {E} _{X}[V(X)].}$$

Доказательство:

Пусть будет свернутой случайной величиной с функцией плотности вероятности (т.е. константой, равной нулю). Пусть случайный вектор и преобразование определяются как ${\displaystyle Z}$ ${\displaystyle p_{Z}(z)=\delta (z)}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle H}$ $${\displaystyle H(Z,X)={\begin{bmatrix}Z+V(X)\\X\end{bmatrix}}={\begin{bmatrix}Y\\{\tilde {X}}\end{bmatrix}}.}$$

Ясно, что является биективным отображением, а якобиан определяется выражением: которая является верхней треугольной матрицей с единицами на главной диагонали, поэтому ее определитель равен 1. Применяя теорему о замене переменной из предыдущего раздела, получаем то, что при маргинализации приводит к искомой функции плотности вероятности. ${\displaystyle H}$ ${\displaystyle H^{-1}}$ $${\displaystyle {\frac {dH^{-1}(y,{\tilde {\mathbf {x} }})}{dy\,d{\tilde {\mathbf {x} }}}}={\begin{bmatrix}1&-{\frac {dV({\tilde {\mathbf {x} }})}{d{\tilde {\mathbf {x} }}}}\\\mathbf {0} _{n\times 1}&\mathbf {I} _{n\times n}\end{bmatrix}},}$$ $${\displaystyle f_{Y,X}(y,x)=f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )},}$$ ${\displaystyle x}$

Суммы независимых случайных величин

Функция плотности вероятности суммы двух независимых случайных величин U и V , каждая из которых имеет функцию плотности вероятности, представляет собой свертку их отдельных функций плотности: $${\displaystyle f_{U+V}(x)=\int _{-\infty }^{\infty }f_{U}(y)f_{V}(x-y)\,dy=\left(f_{U}*f_{V}\right)(x)}$$

Предыдущее соотношение можно обобщить на сумму N независимых случайных величин с плотностями U ₁ , ..., U _N : $${\displaystyle f_{U_{1}+\cdots +U}(x)=\left(f_{U_{1}}*\cdots *f_{U_{N}}\right)(x)}$$

Это можно вывести из двусторонней замены переменных, включающей Y = U + V и Z = V , аналогично примеру ниже для частного независимых случайных величин.

Произведения и частные независимых случайных величин

Если даны две независимые случайные величины U и V , каждая из которых имеет функцию плотности вероятности, то плотность произведения Y = UV и частного Y = U / V можно вычислить путем замены переменных.

Пример: распределение частного

Чтобы вычислить частное Y = U / V двух независимых случайных величин U и V , определим следующее преобразование: $${\displaystyle {\begin{aligned}Y&=U/V\\[1ex]Z&=V\end{aligned}}}$$

Затем совместную плотность p ( y , z ) можно вычислить путем замены переменных с U , V на Y , Z , а Y можно вывести путем исключения Z из совместной плотности.

Обратное преобразование: $${\displaystyle {\begin{aligned}U&=YZ\\V&=Z\end{aligned}}}$$

Абсолютное значение определителя матрицы Якоби этого преобразования равно: ${\displaystyle J(U,V\mid Y,Z)}$ $${\displaystyle \left|\det {\begin{bmatrix}{\frac {\partial u}{\partial y}}&{\frac {\partial u}{\partial z}}\\{\frac {\partial v}{\partial y}}&{\frac {\partial v}{\partial z}}\end{bmatrix}}\right|=\left|\det {\begin{bmatrix}z&y\\0&1\end{bmatrix}}\right|=|z|.}$$

Таким образом: $${\displaystyle p(y,z)=p(u,v)\,J(u,v\mid y,z)=p(u)\,p(v)\,J(u,v\mid y,z)=p_{U}(yz)\,p_{V}(z)\,|z|.}$$

А распределение Y можно вычислить, исключив Z : $${\displaystyle p(y)=\int _{-\infty }^{\infty }p_{U}(yz)\,p_{V}(z)\,|z|\,dz}$$

Этот метод принципиально требует, чтобы преобразование из U , V в Y , Z было биективным . Вышеуказанное преобразование соответствует этому, поскольку Z может быть отображено непосредственно обратно в V , и для заданного V частное U / V является монотонным . Это аналогично имеет место для суммы U + V , разности U − V и произведения UV .

Точно такой же метод можно использовать для вычисления распределения других функций нескольких независимых случайных величин.

Пример: Частное двух стандартных нормалей

При наличии двух стандартных нормальных переменных U и V частное можно вычислить следующим образом. Во-первых, переменные имеют следующие функции плотности: $${\displaystyle {\begin{aligned}p(u)&={\frac {1}{\sqrt {2\pi }}}e^{-{u^{2}}/{2}}\\[1ex]p(v)&={\frac {1}{\sqrt {2\pi }}}e^{-{v^{2}}/{2}}\end{aligned}}}$$

Преобразуем, как описано выше: $${\displaystyle {\begin{aligned}Y&=U/V\\[1ex]Z&=V\end{aligned}}}$$

Это приводит к: $${\displaystyle {\begin{aligned}p(y)&=\int _{-\infty }^{\infty }p_{U}(yz)\,p_{V}(z)\,|z|\,dz\\[5pt]&=\int _{-\infty }^{\infty }{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}y^{2}z^{2}}{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}z^{2}}|z|\,dz\\[5pt]&=\int _{-\infty }^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}\left(y^{2}+1\right)z^{2}}|z|\,dz\\[5pt]&=2\int _{0}^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}\left(y^{2}+1\right)z^{2}}z\,dz\\[5pt]&=\int _{0}^{\infty }{\frac {1}{\pi }}e^{-\left(y^{2}+1\right)u}\,du&&u={\tfrac {1}{2}}z^{2}\\[5pt]&=\left.-{\frac {1}{\pi \left(y^{2}+1\right)}}e^{-\left(y^{2}+1\right)u}\right|_{u=0}^{\infty }\\[5pt]&={\frac {1}{\pi \left(y^{2}+1\right)}}\end{aligned}}}$$

Это плотность стандартного распределения Коши .

Смотрите также

• Оценка плотности  – Оценка ненаблюдаемой базовой функции плотности вероятности.
• Оценка плотности ядра  – EstimatorPages displaying short descriptions with no spaces
• Функция правдоподобия  – функция, связанная со статистикой и теорией вероятностей.
• Список вероятностных распределений
• Амплитуда вероятности  – комплексное число, квадрат абсолютной величины которого является вероятностью.
• Функция массы вероятности  – Дискретно-переменное распределение вероятностей
• Вторичная мера
• Использует в качестве плотности вероятности положения :
  • Атомная орбиталь  – функция, описывающая электрон в атоме.
  • Ареал обитания  — территория, на которой животное живет и периодически перемещается.

Ссылки

1. "AP Statistics Review - Density Curves and the Normal Distributions". Архивировано из оригинала 2 апреля 2015 г. Получено 16 марта 2015 г.
2. Гринстед, Чарльз М.; Снелл, Дж. Лори (2009). "Условная вероятность - дискретная условная" (PDF) . Введение Гринстеда и Снелла в вероятность . Тексты Orange Grove. ISBN 978-1616100469. Архивировано (PDF) из оригинала 2003-04-25 . Получено 2019-07-25 .
3. "вероятность - является ли равномерно случайное число на действительной прямой допустимым распределением?". Перекрестная проверка . Получено 2021-10-06 .
4. Орд, Дж. К. (1972) Семейства распределений частот , Гриффин. ISBN 0-85264-137-0 (например, Таблица 5.1 и Пример 5.4) 
5. Сигрист, Кайл. «Преобразования случайных величин». LibreTexts Statistics . Получено 22 декабря 2023 г.
6. Девор, Джей Л.; Берк, Кеннет Н. (2007). Современная математическая статистика и ее приложения. Cengage. стр. 263. ISBN 978-0-534-40473-4.
7. Дэвид, Стирзакер (2007-01-01). Элементарная вероятность . Cambridge University Press. ISBN 978-0521534284. OCLC  851313783.

Дальнейшее чтение

• Биллингсли, Патрик (1979). Вероятность и мера . Нью-Йорк, Торонто, Лондон: John Wiley and Sons. ISBN 0-471-00710-2.
• Казелла, Джордж ; Бергер, Роджер Л. (2002). Статистический вывод (Второе издание). Thomson Learning. С. 34–37. ISBN 0-534-24312-6.
• Стирзакер, Дэвид (2003). Элементарная вероятность . Издательство Кембриджского университета. ISBN 0-521-42028-8.Главы 7–9 посвящены непрерывным переменным.

Внешние ссылки

• Ушаков, Н.Г. (2001) [1994], "Плотность распределения вероятностей", Энциклопедия математики , Издательство EMS
• Вайсштейн, Эрик В. "Функция плотности вероятности". MathWorld .