Подъемная сила (сила)

Сила, перпендикулярная потоку окружающей жидкости

Планер Райт 1902 года демонстрирует подъемную силу, подтягиваясь вверх

Когда жидкость обтекает объект, жидкость оказывает на объект силу . Подъемная сила — это компонент этой силы, перпендикулярный направлению встречного потока. ^[1] Она контрастирует с силой сопротивления , которая является компонентом силы, параллельной направлению потока. Подъемная сила обычно действует в направлении вверх, чтобы противостоять силе тяжести , но она определяется как действующая перпендикулярно потоку и, следовательно, может действовать в любом направлении.

Если окружающая жидкость — воздух, сила называется аэродинамической силой . В воде или любой другой жидкости она называется гидродинамической силой .

Динамическая подъемная сила отличается от других видов подъемной силы в жидкостях. Аэростатическая подъемная сила или плавучесть , при которой внутренняя жидкость легче окружающей жидкости, не требует движения и используется воздушными шарами, дирижаблями, дирижаблями, лодками и подводными лодками. Глиссирующая подъемная сила , при которой только нижняя часть тела погружена в поток жидкости, используется моторными лодками, досками для серфинга, виндсерферами, парусными лодками и водными лыжами.

Обзор

Подъемная сила определяется как составляющая аэродинамической силы , перпендикулярная направлению потока, а сопротивление — как составляющая, параллельная направлению потока.

Жидкость , текущая вокруг поверхности твердого объекта, прикладывает к нему силу . Не имеет значения, движется ли объект через неподвижную жидкость (например, самолет, летящий по воздуху) или объект неподвижен, а жидкость движется (например, крыло в аэродинамической трубе) или движутся оба (например, парусник, использующий ветер для движения вперед). Подъемная сила — это составляющая этой силы, которая перпендикулярна направлению набегающего потока. ^[1] Подъемная сила всегда сопровождается силой сопротивления , которая является составляющей поверхностной силы, параллельной направлению потока.

Подъемная сила в основном связана с крыльями самолетов с фиксированным крылом , хотя она более широко создается многими другими обтекаемыми телами, такими как пропеллеры , воздушные змеи , роторы вертолетов , крылья гоночных автомобилей , морские паруса , ветряные турбины , а также кили парусных лодок , рули кораблей и подводные крылья в воде. Подъемная сила также используется летающими и планирующими животными , особенно птицами , летучими мышами и насекомыми , и даже в растительном мире семенами некоторых деревьев. ^[2] Хотя общее значение слова «подъемная сила» предполагает, что подъемная сила противодействует весу, подъемная сила может быть в любом направлении относительно силы тяжести, поскольку она определяется относительно направления потока, а не направления силы тяжести. Когда самолет движется по прямой и горизонтальному маршруту, большая часть подъемной силы противодействует силе тяжести. ^[3] Однако, когда самолет поднимается , опускается или делает вираж на повороте, подъемная сила наклонена относительно вертикали. ^[4] Подъемная сила может также действовать как прижимная сила в некоторых фигурах высшего пилотажа или на крыле гоночного автомобиля. Подъемная сила может также быть в значительной степени горизонтальной, например, на парусном судне.

Подъемная сила, обсуждаемая в этой статье, в основном связана с аэродинамическими профилями, хотя морские подводные крылья и гребные винты имеют одни и те же физические принципы и работают одинаково, несмотря на такие различия между воздухом и водой, как плотность, сжимаемость и вязкость.

Поток вокруг подъемного профиля представляет собой явление механики жидкости , которое можно понять по существу на двух уровнях: существуют математические теории, которые основаны на установленных законах физики и точно представляют поток, но которые требуют решения уравнений в частных производных. И существуют физические объяснения без математики, которые менее строги. ^[5] Правильно объяснить подъемную силу в этих качественных терминах сложно, поскольку причинно-следственные связи, вовлеченные в процесс, являются тонкими. ^[6] Всеобъемлющее объяснение, которое охватывает все существенные аспекты, обязательно является сложным. Существует также много упрощенных объяснений, но все они оставляют существенные части явления необъясненными, в то время как некоторые также имеют элементы, которые просто неверны. ^{[5] [7] [8] [9] [10] [11]}

Упрощенные физические объяснения подъемной силы на аэродинамическом профиле

Поперечное сечение крыла определяет форму аэродинамического профиля.

Аэродинамический профиль — это обтекаемая форма, которая способна создавать значительно большую подъемную силу, чем сопротивление. ^[12] Плоская пластина может создавать подъемную силу, но не такую ​​большую, как обтекаемый аэродинамический профиль, и с несколько большим сопротивлением. Большинство упрощенных объяснений следуют одному из двух основных подходов, основанных либо на законах движения Ньютона , либо на принципе Бернулли . ^{[5] [13] [14] [15]}

Объяснение, основанное на отклонении потока и законах Ньютона.

Когда крыло создает подъемную силу, оно отклоняет воздух вниз, и для этого оно должно оказывать на воздух направленную вниз силу. Третий закон Ньютона требует, чтобы воздух оказывал на крыло равную направленную вверх силу.

Аэродинамический профиль создает подъемную силу, оказывая направленную вниз на воздух, когда он течет мимо. Согласно третьему закону Ньютона , воздух должен оказывать равную и противоположную (восходящую) силу на аэродинамический профиль, которая и является подъемной силой. ^{[16] [17] [18] [19]}

Когда воздушный поток приближается к аэродинамическому профилю, он изгибается вверх, но когда он проходит аэродинамический профиль, он меняет направление и следует по траектории, которая изгибается вниз. Согласно второму закону Ньютона, это изменение направления потока требует силы, направленной вниз, приложенной к воздуху аэродинамическим профилем. Затем третий закон Ньютона требует, чтобы воздух оказывал восходящую силу на аэродинамический профиль; таким образом, сила реакции, подъемная сила, создается противоположно изменению направления. В случае крыла самолета крыло оказывает направленную вниз силу на воздух, а воздух оказывает направленную вверх силу на крыло. ^{[20] [21] [22] [23] [24] [25] [ чрезмерное цитирование ]}

Нисходящее направление потока создается не только нижней поверхностью аэродинамического профиля, но и поток воздуха над аэродинамическим профилем в значительной степени отвечает за нисходящее направление. ^{[26] [27] [28] [29]}

Это объяснение верно, но оно неполное. Оно не объясняет, как аэродинамический профиль может придать нисходящий поворот гораздо более глубокой полосе потока, чем та, которой он фактически касается. Кроме того, оно не упоминает, что подъемная сила создается разницей давления, и не объясняет, как эта разница давления поддерживается. ^[5]

Споры относительно эффекта Коанды

Некоторые версии объяснения подъемной силы отклонением потока ссылаются на эффект Коанда как на причину, по которой поток может следовать за выпуклой верхней поверхностью аэродинамического профиля. Традиционное определение в области аэродинамики заключается в том, что эффект Коанда относится к тенденции струи жидкости оставаться прикрепленной к смежной поверхности, которая изгибается в сторону от потока, и к результирующему вовлечению окружающего воздуха в поток. ^{[30] [31] [32]}

В более широком смысле некоторые считают, что эффект включает тенденцию любого пограничного слоя жидкости прилипать к изогнутой поверхности, а не только пограничный слой, сопровождающий струю жидкости. Именно в этом более широком смысле эффект Коанды используется некоторыми популярными источниками для объяснения того, почему поток воздуха остается прикрепленным к верхней стороне аэродинамического профиля. ^{[33] [34]} Это спорное использование термина «эффект Коанды»; поток, следующий за верхней поверхностью, просто отражает отсутствие разделения пограничного слоя, поэтому это не пример эффекта Коанды. ^{[35] [36] [37] [38]} Независимо от того, применимо ли это более широкое определение «эффекта Коанды», называние его «эффектом Коанды» не дает объяснения, оно просто дает явлению название. ^[39]

Способность потока жидкости следовать по криволинейной траектории не зависит от сдвигающих сил, вязкости жидкости или наличия пограничного слоя. Воздух, обтекающий аэродинамический профиль, прилипающий как к верхней, так и к нижней поверхностям и создающий подъемную силу, принимается как явление в невязком потоке. ^[40]

Объяснения, основанные на увеличении скорости потока и принципе Бернулли

Существуют две распространённые версии этого объяснения: одна основана на «равном времени прохождения», а другая — на «препятствии» воздушному потоку.

Иллюстрация неправильного объяснения подъемной силы аэродинамического профиля с помощью принципа равного времени прохождения. ^[7]

Ложное объяснение, основанное на равном времени прохождения

Объяснение «равного времени прохождения» начинается с утверждения, что поток над верхней поверхностью быстрее, чем поток над нижней поверхностью, потому что длина пути над верхней поверхностью больше и должна быть пройдена за равное время прохождения. ^{[41] [42] [43]} Принцип Бернулли гласит, что при определенных условиях увеличение скорости потока связано с уменьшением давления. Сделан вывод, что уменьшение давления над верхней поверхностью приводит к подъему вверх. ^[44]

Хотя верно, что поток ускоряется, серьезным недостатком этого объяснения является то, что оно неправильно объясняет, что заставляет поток ускоряться. ^[5] Объяснение с большей длиной пути неверно. Никакой разницы в длине пути не требуется, и даже когда разница есть, она, как правило, слишком мала, чтобы объяснить наблюдаемую разницу в скорости. ^[45] Это происходит потому, что предположение о равном времени прохождения неверно, когда применяется к телу, создающему подъемную силу. Не существует физического принципа, который требует равного времени прохождения во всех ситуациях, и экспериментальные результаты подтверждают, что для тела, создающего подъемную силу, время прохождения не равно. ^{[46] [47] [48] [49] [50] [51]} Фактически, воздух, движущийся мимо верхней части аэродинамического профиля, создающего подъемную силу, движется намного быстрее, чем предсказывает равное время прохождения. ^[52] Гораздо более высокая скорость потока над верхней поверхностью может быть четко видна на этой анимированной визуализации потока.

Препятствие потоку воздуха

Линии тока и трубки тока вокруг аэродинамического профиля, создающего подъемную силу. Поток двумерный, а аэродинамический профиль имеет бесконечный размах. Обратите внимание на более узкие трубки тока вверху и более широкие трубки тока внизу.

Подобно объяснению с равным временем прохождения, объяснение «препятствия» или «защемления трубки потока» утверждает, что поток над верхней поверхностью быстрее, чем поток над нижней поверхностью, но дает другую причину разницы в скорости. Оно утверждает, что изогнутая верхняя поверхность действует как большее препятствие для потока, заставляя линии тока сжиматься ближе друг к другу, делая трубки потока уже. Когда трубки потока становятся уже, сохранение массы требует, чтобы скорость потока должна была увеличиться. ^[53] Уменьшенное давление на верхней поверхности и восходящая подъемная сила следуют из более высокой скорости по принципу Бернулли , как и в объяснении с равным временем прохождения. Иногда проводится аналогия с соплом Вентури , утверждая, что верхняя поверхность крыла действует как сопло Вентури, ограничивая поток. ^[54]

Один серьезный недостаток объяснения с помощью препятствия заключается в том, что оно не объясняет, как происходит защемление трубки потока или почему оно больше над верхней поверхностью, чем над нижней поверхностью. Для обычных крыльев, которые плоские снизу и изогнуты сверху, это имеет некоторый интуитивный смысл, но это не объясняет, как плоские пластины, симметричные аэродинамические профили, паруса парусных лодок или обычные аэродинамические профили, летящие вверх ногами, могут создавать подъемную силу, а попытки рассчитать подъемную силу на основе величины сужения или препятствия не предсказывают экспериментальные результаты. ^{[55] [56] [57] [58]} Другой недостаток заключается в том, что сохранение массы не является удовлетворительной физической причиной, по которой поток будет ускоряться. Эффективное объяснение ускорения объекта требует определения силы, которая его ускоряет. ^[59]

Проблемы, общие для обеих версий объяснения на основе теории Бернулли

Серьезный недостаток, общий для всех объяснений, основанных на принципе Бернулли, заключается в том, что они подразумевают, что разница в скорости может возникать по причинам, отличным от разницы в давлении, и что разница в скорости затем приводит к разнице в давлении, согласно принципу Бернулли. Эта подразумеваемая односторонняя причинно-следственная связь является заблуждением. Реальная связь между давлением и скоростью потока является взаимным взаимодействием. ^[5] Как объясняется ниже в более полном физическом объяснении, создание подъемной силы требует поддержания разницы давления как в вертикальном, так и в горизонтальном направлениях. Объяснения, основанные только на принципе Бернулли, не объясняют, как поддерживаются разницы давления в вертикальном направлении. То есть они опускают часть взаимодействия, связанную с отклонением потока. ^[5]

Хотя два простых объяснения, основанных на законе Бернулли, приведенные выше, неверны, нет ничего неправильного в принципе Бернулли или в том факте, что воздух движется быстрее на верхней части крыла, и принцип Бернулли можно правильно использовать как часть более сложного объяснения подъемной силы. ^[60]

Основные характеристики лифта

Подъемная сила является результатом разницы давления и зависит от угла атаки, формы аэродинамического профиля, плотности воздуха и скорости полета.

Перепады давления

Давление — это нормальная сила на единицу площади, оказываемая воздухом на себя и на поверхности, которых он касается. Подъемная сила передается через давление, которое действует перпендикулярно поверхности аэродинамического профиля. Таким образом, чистая сила проявляется как разность давлений. Направление чистой силы подразумевает, что среднее давление на верхней поверхности аэродинамического профиля ниже, чем среднее давление на нижней стороне. ^[61]

Эти перепады давления возникают в связи с искривленным потоком воздуха. Когда жидкость следует по искривленному пути, существует градиент давления , перпендикулярный направлению потока, с более высоким давлением снаружи кривой и более низким давлением внутри. ^[62] Эта прямая связь между искривленными линиями тока и перепадами давления, иногда называемая теоремой о кривизне линий тока , была выведена из второго закона Ньютона Леонардом Эйлером в 1754 году:

${\displaystyle {\frac {\operatorname {d} p}{\operatorname {d} R}}=\rho {\frac {v^{2}}{R}}}$

Левая часть этого уравнения представляет собой разницу давлений, перпендикулярную потоку жидкости. В правой части уравнения ρ — плотность, v — скорость, а R — радиус кривизны. Эта формула показывает, что более высокие скорости и более узкие кривизны создают большие перепады давления, а для прямого потока (R → ∞) разница давлений равна нулю. ^[63]

Угол атаки

Угол атаки аэродинамического профиля

Угол атаки — это угол между хордой профиля и набегающим потоком воздуха. Симметричный профиль создает нулевую подъемную силу при нулевом угле атаки. Но по мере увеличения угла атаки воздух отклоняется на больший угол, а вертикальная составляющая скорости воздушного потока увеличивается, что приводит к большей подъемной силе. Для малых углов симметричный профиль создает подъемную силу, примерно пропорциональную углу атаки. ^{[64] [65]}

По мере увеличения угла атаки подъемная сила достигает максимума при некотором угле; увеличение угла атаки сверх этого критического угла атаки приводит к отделению потока верхней поверхности от крыла; происходит меньшее отклонение вниз, поэтому аэродинамический профиль создает меньшую подъемную силу. Говорят, что аэродинамический профиль сваливается . ^[66]

Форма аэродинамического профиля

Аэродинамический профиль с выпуклостью по сравнению с симметричным аэродинамическим профилем

Максимальная подъемная сила, которая может быть создана аэродинамическим профилем при заданной скорости полета, зависит от формы аэродинамического профиля, особенно от величины изгиба (кривизна, при которой верхняя поверхность более выпуклая, чем нижняя, как показано справа). Увеличение изгиба обычно увеличивает максимальную подъемную силу при заданной скорости полета. ^{[67] [68]}

Выпуклые аэродинамические профили создают подъемную силу при нулевом угле атаки. Когда хорда горизонтальна, задняя кромка имеет направление вниз, и поскольку воздух следует за задней кромкой, он отклоняется вниз. ^[69] Когда выгнутый аэродинамический профиль перевернут, угол атаки можно отрегулировать так, чтобы подъемная сила была направлена ​​вверх. Это объясняет, как самолет может летать вверх ногами. ^{[70] [71]}

Условия потока

Условия окружающего потока, которые влияют на подъемную силу, включают плотность жидкости, вязкость и скорость потока. Плотность зависит от температуры и акустической скорости среды – т.е. от эффектов сжимаемости.

Скорость и плотность воздуха

Подъемная сила пропорциональна плотности воздуха и приблизительно пропорциональна квадрату скорости потока. Подъемная сила также зависит от размера крыла, будучи, как правило, пропорциональной площади крыла, проецируемой в направлении подъемной силы. В расчетах удобно количественно определять подъемную силу в терминах коэффициента подъемной силы, основанного на этих факторах.

Пограничный слой и профильное сопротивление

Независимо от того, насколько гладкой кажется поверхность аэродинамического профиля, любая поверхность является шероховатой в масштабе молекул воздуха. Молекулы воздуха, влетающие в поверхность, отскакивают от шероховатой поверхности в случайных направлениях относительно их исходных скоростей. В результате, когда воздух рассматривается как сплошной материал, он не может скользить по поверхности, и скорость воздуха относительно аэродинамического профиля уменьшается почти до нуля на поверхности (т. е. молекулы воздуха «прилипают» к поверхности, а не скользят по ней), что известно как условие отсутствия скольжения . ^[72] Поскольку воздух у поверхности имеет близкую к нулю скорость, но воздух вдали от поверхности движется, существует тонкий пограничный слой, в котором воздух вблизи поверхности подвергается сдвиговому движению . ^{[73] [74]} Вязкость воздуха сопротивляется сдвигу, вызывая сдвиговое напряжение на поверхности аэродинамического профиля, называемое сопротивлением трения поверхности . На большей части поверхности большинства аэродинамических профилей пограничный слой является естественно турбулентным, что увеличивает сопротивление трения поверхности. ^{[74] [75]}

В обычных условиях полета пограничный слой остается прикрепленным как к верхней, так и к нижней поверхности вплоть до задней кромки, и его влияние на остальную часть потока скромное. По сравнению с предсказаниями теории невязкого потока , в которой нет пограничного слоя, прикрепленный пограничный слой уменьшает подъемную силу на небольшую величину и несколько изменяет распределение давления, что приводит к сопротивлению давления, связанному с вязкостью, сверх сопротивления трения поверхности. Сумма сопротивления трения поверхности и сопротивления давления, связанного с вязкостью, обычно называется профильным сопротивлением . ^{[75] [76]}

Срыв

Воздушный поток, отделяющийся от крыла под большим углом атаки

Максимальная подъемная сила аэродинамического профиля при заданной скорости полета ограничена отрывом пограничного слоя . По мере увеличения угла атаки достигается точка, в которой пограничный слой больше не может оставаться прикрепленным к верхней поверхности. Когда пограничный слой отделяется, он оставляет область рециркуляционного потока над верхней поверхностью, как показано на фотографии визуализации потока справа. Это известно как срыв или сваливание . При углах атаки выше срыва подъемная сила значительно уменьшается, хотя и не падает до нуля. Максимальная подъемная сила, которая может быть достигнута до срыва, с точки зрения коэффициента подъемной силы, обычно составляет менее 1,5 для одноэлементных аэродинамических профилей и может быть более 3,0 для аэродинамических профилей с высокоподъемными щелевыми закрылками и развернутыми устройствами передней кромки. ^[77]

Тела блефа

Поток вокруг плохо обтекаемых тел – т. е. без обтекаемой формы или срывающихся аэродинамических профилей – может также создавать подъемную силу, в дополнение к сильной силе сопротивления. Эта подъемная сила может быть постоянной или колебаться из -за вихреобразования . Взаимодействие гибкости объекта с вихреобразованием может усиливать эффекты флуктуирующей подъемной силы и вызывать вызванные вихрем колебания . ^[78] Например, поток вокруг круглого цилиндра создает вихревую дорожку Кармана : вихри попеременно сбрасываются со сторон цилиндра. Колебательная природа потока создает флуктуирующую подъемную силу на цилиндре, хотя чистая (средняя) сила пренебрежимо мала. Частота подъемной силы характеризуется безразмерным числом Струхаля , которое зависит от числа Рейнольдса потока. ^{[79] [80]}

Для гибкой конструкции эта колебательная подъемная сила может вызывать вибрации, вызванные вихрем. При определенных условиях – например, резонансе или сильной корреляции подъемной силы по размаху – результирующее движение конструкции из-за колебаний подъемной силы может быть значительно усилено. Такие вибрации могут создавать проблемы и угрожать обрушением высоких искусственных сооружений, таких как промышленные дымоходы . ^[78]

В эффекте Магнуса подъемная сила создается вращающимся цилиндром в свободном потоке. Здесь механическое вращение действует на пограничный слой, заставляя его разделяться в разных местах по обе стороны цилиндра. Асимметричное разделение изменяет эффективную форму цилиндра в том, что касается потока, так что цилиндр действует как подъемный аэродинамический профиль с циркуляцией во внешнем потоке. ^[81]

Более полное физическое объяснение

Как описано выше в разделе «Упрощенные физические объяснения подъемной силы на аэродинамическом профиле», существует два основных популярных объяснения: одно основано на отклонении потока вниз (законы Ньютона), а другое основано на разнице давления, сопровождающейся изменениями скорости потока (принцип Бернулли). Каждое из них само по себе правильно определяет некоторые аспекты подъемного потока, но оставляет другие важные аспекты явления необъясненными. Более полное объяснение включает как отклонение вниз, так и разницу давления (включая изменения скорости потока, связанные с разницей давления), и требует более подробного рассмотрения потока. ^[82]

Подъемная сила на поверхности аэродинамического профиля

Форма профиля и угол атаки работают вместе, так что профиль оказывает направленную вниз силу на воздух, когда он течет мимо. Согласно третьему закону Ньютона, воздух должен затем оказывать равную и противоположную (направленную вверх) силу на профиль, которая является подъемной силой. ^[18]

Чистая сила, оказываемая воздухом, возникает как разность давлений на поверхностях аэродинамического профиля. ^[83] Давление в жидкости всегда положительно в абсолютном смысле, ^[84] поэтому давление всегда следует рассматривать как толкающее, а не как тянущее. Таким образом, давление толкает аэродинамический профиль внутрь везде на верхней и нижней поверхностях. Текущий воздух реагирует на присутствие крыла, уменьшая давление на верхнюю поверхность крыла и увеличивая давление на нижнюю поверхность. Давление на нижней поверхности толкает вверх сильнее, чем уменьшенное давление на верхней поверхности толкает вниз, и конечный результат — подъемная сила вверх. ^[83]

Разница давлений, которая приводит к подъемной силе, воздействует непосредственно на поверхности аэродинамического профиля; однако для понимания того, как создается разница давлений, необходимо понимать, что происходит с потоком на более широкой площади.

Более широкий поток вокруг аэродинамического профиля

Поток вокруг аэродинамического профиля: точки движутся вместе с потоком. Черные точки находятся на временных срезах , которые разделяются на две части — верхнюю и нижнюю — на передней кромке. Заметная разница в скорости между линиями тока верхней и нижней поверхности наиболее четко показана на анимации изображения, при этом верхние маркеры достигают задней кромки задолго до нижних. Цвета точек обозначают линии тока .

Аэродинамический профиль влияет на скорость и направление потока на большой площади, создавая картину, называемую полем скорости . Когда аэродинамический профиль создает подъемную силу, поток перед аэродинамическим профилем отклоняется вверх, поток над и под аэродинамическим профилем отклоняется вниз, оставляя воздух далеко позади аэродинамического профиля в том же состоянии, что и набегающий поток далеко впереди. Поток над верхней поверхностью ускоряется, в то время как поток под аэродинамическим профилем замедляется. Вместе с отклонением вверх воздуха впереди и отклонением вниз воздуха сразу позади это устанавливает чистую циркуляционную составляющую потока. Отклонение вниз и изменения скорости потока выражены и распространяются на большую площадь, как можно увидеть на анимации потока справа. Эти различия в направлении и скорости потока наибольшие вблизи аэродинамического профиля и постепенно уменьшаются далеко выше и ниже. Все эти особенности поля скорости также появляются в теоретических моделях для подъемных потоков. ^{[85] [86]}

Давление также влияет на широкую область, в виде неоднородного давления, называемого полем давления . Когда аэродинамический профиль создает подъемную силу, над аэродинамическим профилем имеется диффузная область низкого давления, а под ним обычно диффузная область высокого давления, как показано изобарами (кривыми постоянного давления) на рисунке. Разница давлений, которая действует на поверхность, является лишь частью этого поля давления. ^[87]

Взаимное влияние перепадов давления и изменений скорости потока

Поле давления вокруг аэродинамического профиля. Линии — изобары одинакового давления по всей длине. Стрелки показывают перепад давления от высокого (красный) до низкого (синий) и, следовательно, также чистую силу, которая заставляет воздух ускоряться в этом направлении.

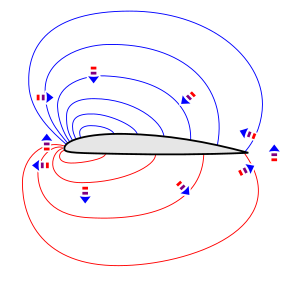
Неравномерное давление оказывает силы на воздух в направлении от более высокого давления к более низкому давлению. Направление силы различно в разных местах вокруг аэродинамического профиля, как указано стрелками блока в поле давления вокруг фигуры аэродинамического профиля. Воздух над аэродинамическим профилем выталкивается к центру области низкого давления, а воздух под аэродинамическим профилем выталкивается наружу из центра области высокого давления.

Согласно второму закону Ньютона , сила заставляет воздух ускоряться в направлении силы. Таким образом, вертикальные стрелки на прилагаемой диаграмме поля давления указывают, что воздух над и под аэродинамическим профилем ускоряется или поворачивается вниз, и что неравномерное давление, таким образом, является причиной отклонения потока вниз, видимого в анимации потока. Чтобы произвести этот поворот вниз, аэродинамический профиль должен иметь положительный угол атаки или иметь достаточный положительный изгиб. Обратите внимание, что поворот потока вниз над верхней поверхностью является результатом того, что воздух выталкивается вниз более высоким давлением над ним, чем под ним. Некоторые объяснения, которые ссылаются на «эффект Коанды», предполагают, что вязкость играет ключевую роль в повороте вниз, но это неверно. (см. выше в разделе «Споры относительно эффекта Коанды»).

Стрелки перед профилем указывают на то, что поток перед профилем отклоняется вверх, а стрелки за профилем указывают на то, что поток за профилем снова отклоняется вверх после отклонения вниз по профилю. Эти отклонения также видны в анимации потока.

Стрелки впереди и позади аэродинамического профиля также указывают на то, что воздух, проходящий через область низкого давления над аэродинамическим профилем, ускоряется при входе и замедляется при выходе. Воздух, проходящий через область высокого давления под аэродинамическим профилем, замедляется при входе и ускоряется при выходе. Таким образом, неравномерное давление также является причиной изменений скорости потока, видимых в анимации потока. Изменения скорости потока согласуются с принципом Бернулли , который гласит, что в устойчивом потоке без вязкости более низкое давление означает более высокую скорость, а более высокое давление означает более низкую скорость.

Таким образом, изменения направления и скорости потока напрямую вызваны неравномерным давлением. Но эта причинно-следственная связь не является односторонней; она работает в обоих направлениях одновременно. Движение воздуха зависит от разницы давления, но существование разницы давления зависит от движения воздуха. Таким образом, эта связь является взаимным или реципрокным взаимодействием: воздушный поток изменяет скорость или направление в ответ на разницу давления, а разница давления поддерживается сопротивлением воздуха изменению скорости или направления. ^[88] Разница давления может существовать только в том случае, если есть что-то, от чего она может отталкиваться. В аэродинамическом потоке разница давления отталкивается от инерции воздуха, поскольку воздух ускоряется разницей давления. ^[89] Вот почему масса воздуха является частью расчета, и почему подъемная сила зависит от плотности воздуха.

Поддержание разницы давления, которая оказывает подъемную силу на поверхности аэродинамического профиля, требует поддержания картины неравномерного давления в широкой области вокруг аэродинамического профиля. Это требует поддержания разницы давления как в вертикальном, так и в горизонтальном направлениях, и, таким образом, требует как поворота потока вниз, так и изменения скорости потока в соответствии с принципом Бернулли. Разница давления и изменения направления и скорости потока поддерживают друг друга во взаимном взаимодействии. Разница давления естественным образом вытекает из второго закона Ньютона и из того факта, что поток вдоль поверхности следует преимущественно наклонным вниз контурам аэродинамического профиля. И тот факт, что воздух имеет массу, имеет решающее значение для взаимодействия. ^[90]

Насколько несостоятельны простые объяснения

Создание подъемной силы требует как поворота потока вниз, так и изменения скорости потока в соответствии с принципом Бернулли. Каждое из упрощенных объяснений, приведенных выше в разделе «Упрощенные физические объяснения подъемной силы на аэродинамическом профиле», не оправдывает ожиданий, пытаясь объяснить подъемную силу в терминах только одного или другого, тем самым объясняя только часть явления и оставляя другие части необъясненными. ^[91]

Количественная оценка подъема

Интеграция давления

Когда распределение давления на поверхности аэродинамического профиля известно, определение общей подъемной силы требует сложения вкладов в силу давления от локальных элементов поверхности, каждый из которых имеет свое собственное локальное значение давления. Таким образом, общая подъемная сила является интегралом давления в направлении, перпендикулярном потоку дальнего поля, по поверхности аэродинамического профиля. ^[92]

${\displaystyle L=\oint p\mathbf {n} \cdot \mathbf {k} \;\mathrm {d} S,}$

где:

• S — проецируемая (в плане) площадь аэродинамического профиля, измеренная перпендикулярно среднему потоку воздуха;
• n — нормальный единичный вектор, направленный внутрь крыла;
• k — вертикальный единичный вектор, перпендикулярный направлению свободного потока .

Приведенное выше уравнение подъемной силы не учитывает силы трения поверхности , которые малы по сравнению с силами давления.

Используя продольный вектор i, параллельный набегающему потоку, вместо k в интеграле, мы получаем выражение для сопротивления давления D _p (которое включает в себя часть давления сопротивления профиля и, если крыло трехмерное, индуктивное сопротивление). Если мы используем продольный вектор j , мы получаем боковую силу Y .

${\displaystyle {\begin{aligned}D_{p}&=\oint p\mathbf {n} \cdot \mathbf {i} \;\mathrm {d} S,\\Y&=\oint p\mathbf {n} \cdot \mathbf {j} \;\mathrm {d} S.\end{aligned}}}$

Для справедливости этого интегрирования обычно требуется, чтобы форма аэродинамического профиля представляла собой замкнутую кусочно-гладкую кривую .

Коэффициент подъемной силы

Подъемная сила зависит от размера крыла, будучи приблизительно пропорциональной площади крыла. Часто бывает удобно количественно оценить подъемную силу данного аэродинамического профиля по его коэффициенту подъемной силы , который определяет его общую подъемную силу в терминах единицы площади крыла. ${\displaystyle C_{L}}$

Если задано значение для крыла при заданном угле атаки, то можно определить подъемную силу, создаваемую для конкретных условий потока: ^[93] ${\displaystyle C_{L}}$

${\displaystyle L={\tfrac {1}{2}}\rho v^{2}SC_{L}}$

где

• ${\displaystyle L}$это подъемная сила
• ${\displaystyle \rho }$это плотность воздуха
• ${\displaystyle v}$это скорость или истинная воздушная скорость
• ${\displaystyle S}$это площадь крыла в плане (проекция)
• ${\displaystyle C_{L}}$коэффициент подъемной силы при желаемом угле атаки, числе Маха и числе Рейнольдса ^[94]

Математические теории подъемной силы

Математические теории подъемной силы основаны на механике сплошной жидкости, предполагающей, что воздух течет как непрерывная жидкость. ^{[95] [96] [97]} Подъемная сила создается в соответствии с фундаментальными принципами физики, наиболее важными из которых являются следующие три принципа: ^[98]

• Сохранение импульса , которое является следствием законов движения Ньютона , особенно второго закона Ньютона, который связывает результирующую силу, действующую на элемент воздуха, со скоростью изменения его импульса ,
• Сохранение массы , включая предположение, что поверхность аэродинамического профиля непроницаема для обтекающего ее воздуха, и
• Закон сохранения энергии гласит, что энергия не создается и не уничтожается.

Поскольку аэродинамический профиль влияет на поток в широкой области вокруг него, законы сохранения механики воплощены в форме уравнений в частных производных, объединенных с набором требований граничных условий , которым поток должен удовлетворять на поверхности аэродинамического профиля и вдали от него. ^[99]

Для прогнозирования подъемной силы требуется решение уравнений для конкретной формы аэродинамического профиля и условий потока, что обычно требует вычислений, которые настолько объемны, что их можно выполнить только на компьютере, с помощью методов вычислительной гидродинамики (CFD). Определение чистой аэродинамической силы из решения CFD требует «сложения» ( интегрирования ) сил, вызванных давлением и сдвигом, определяемых CFD по каждому элементу поверхности аэродинамического профиля, как описано в разделе «интегрирование давления».

Уравнения Навье-Стокса (NS) обеспечивают потенциально наиболее точную теорию подъемной силы, но на практике учет эффектов турбулентности в пограничном слое на поверхности аэродинамического профиля требует некоторой потери точности и требует использования усредненных по Рейнольдсу уравнений Навье-Стокса (RANS). Были также разработаны более простые, но менее точные теории.

Уравнения Навье–Стокса (НС)

Эти уравнения представляют собой сохранение массы, второй закон Ньютона (сохранение импульса), сохранение энергии, закон Ньютона для действия вязкости , закон теплопроводности Фурье , уравнение состояния, связывающее плотность, температуру и давление, а также формулы для вязкости и теплопроводности жидкости. ^{[100] [101]}

В принципе, уравнения NS в сочетании с граничными условиями отсутствия сквозного потока и отсутствия скольжения на поверхности аэродинамического профиля могут быть использованы для прогнозирования подъемной силы с высокой точностью в любой ситуации обычного полета в атмосфере. Однако воздушные потоки в практических ситуациях всегда включают турбулентность в пограничном слое рядом с поверхностью аэродинамического профиля, по крайней мере, над задней частью аэродинамического профиля. Прогнозирование подъемной силы путем решения уравнений NS в их необработанной форме потребовало бы расчетов для разрешения деталей турбулентности, вплоть до мельчайших вихрей. Это пока невозможно даже на самом мощном компьютере. ^[102] Таким образом, в принципе, уравнения NS обеспечивают полную и очень точную теорию подъемной силы, но практическое прогнозирование подъемной силы требует, чтобы эффекты турбулентности были смоделированы в уравнениях RANS, а не вычислены напрямую.

Уравнения Навье-Стокса, усредненные по Рейнольдсу (RANS)

Это уравнения NS с турбулентными движениями, усредненными по времени, и влияние турбулентности на усредненный по времени поток, представленное моделированием турбулентности (дополнительный набор уравнений, основанный на сочетании размерного анализа и эмпирической информации о том, как турбулентность влияет на пограничный слой в усредненном по времени смысле). ^{[103] [104]} Решение RANS состоит из усредненного по времени вектора скорости, давления, плотности и температуры, определенных в густой сетке точек, окружающих аэродинамический профиль.

Объем требуемых вычислений составляет ничтожную долю (миллиардную) ^[102] того, что потребовалось бы для разрешения всех турбулентных движений в чистом расчете NS, и с доступными большими компьютерами теперь практично выполнять расчеты RANS для полных самолетов в трех измерениях. Поскольку модели турбулентности несовершенны, точность расчетов RANS несовершенна, но она достаточна для практического проектирования самолетов. Подъемная сила, предсказанная RANS, обычно находится в пределах нескольких процентов от фактической подъемной силы.

Уравнения невязкого течения (Эйлера или потенциала)

Уравнения Эйлера — это уравнения NS без эффектов вязкости, теплопроводности и турбулентности. ^[105] Как и в случае с решением RANS, решение Эйлера состоит из вектора скорости, давления, плотности и температуры, определенных в плотной сетке точек, окружающих аэродинамический профиль. Хотя уравнения Эйлера проще уравнений NS, они не поддаются точным аналитическим решениям.

Дальнейшее упрощение возможно с помощью теории потенциального потока , которая сокращает число неизвестных, подлежащих определению, и делает возможными аналитические решения в некоторых случаях, как описано ниже.

Расчеты Эйлера или потенциального потока предсказывают распределение давления на поверхностях аэродинамического профиля примерно правильно для углов атаки ниже срыва, где они могут не досчитаться общей подъемной силы на целых 10–20%. При углах атаки выше срыва невязкие расчеты не предсказывают, что срыв произошел, и в результате они сильно переоценивают подъемную силу.

В теории потенциального потока предполагается, что поток является безвихревым , т. е. что малые жидкие порции не имеют чистой скорости вращения. Математически это выражается утверждением, что ротор векторного поля скорости везде равен нулю. Безвихревые потоки обладают удобным свойством, заключающимся в том, что скорость может быть выражена как градиент скалярной функции, называемой потенциалом . Поток, представленный таким образом, называется потенциальным потоком. ^{[106] [107] [108] [109]}

В теории потенциального потока поток предполагается несжимаемым. Теория потенциального потока несжимаемой жидкости имеет то преимущество, что уравнение ( уравнение Лапласа ), которое должно быть решено для потенциала, является линейным , что позволяет строить решения путем суперпозиции других известных решений. Уравнение потенциального потока несжимаемой жидкости также может быть решено с помощью конформного отображения , метода, основанного на теории функций комплексной переменной. В начале 20-го века, до появления компьютеров, конформное отображение использовалось для генерации решений уравнения потенциального потока несжимаемой жидкости для класса идеализированных форм аэродинамического профиля, что дало некоторые из первых практических теоретических предсказаний распределения давления на подъемном аэродинамическом профиле.

Решение уравнения потенциала напрямую определяет только поле скорости. Поле давления выводится из поля скорости через уравнение Бернулли.

Сравнение неподъемной модели потока вокруг аэродинамического профиля и подъемной модели потока, соответствующей условию Кутта, при котором поток плавно покидает заднюю кромку

Применение теории потенциального потока к подъемному потоку требует специального рассмотрения и дополнительного предположения. Проблема возникает из-за того, что подъемная сила на аэродинамическом профиле в невязком потоке требует циркуляции в потоке вокруг аэродинамического профиля (см. «Циркуляция и теорема Кутты–Жуковского» ниже), но одна потенциальная функция, непрерывная во всей области вокруг аэродинамического профиля, не может представлять поток с ненулевой циркуляцией. Решение этой проблемы состоит в том, чтобы ввести разрез ответвления , кривую или линию от некоторой точки на поверхности аэродинамического профиля до бесконечности, и разрешить скачок значения потенциала через разрез. Скачок потенциала накладывает циркуляцию в потоке, равную скачку потенциала, и, таким образом, позволяет представить ненулевую циркуляцию. Однако скачок потенциала является свободным параметром, который не определяется уравнением потенциала или другими граничными условиями, и решение, таким образом, является неопределенным. Решение потенциального потока существует для любого значения циркуляции и любого значения подъемной силы. Один из способов разрешения этой неопределенности — наложить условие Кутты , ^{[110] [111]} , которое заключается в том, что из всех возможных решений физически разумным является то, при котором поток плавно покидает заднюю кромку. Эскизы линий тока иллюстрируют одну модель потока с нулевой подъемной силой, при которой поток огибает заднюю кромку и покидает верхнюю поверхность перед задней кромкой, и другую модель потока с положительной подъемной силой, при которой поток плавно покидает заднюю кромку в соответствии с условием Кутты.

Линеаризованный потенциальный поток

Это теория потенциального потока с дополнительными предположениями, что аэродинамический профиль очень тонкий, а угол атаки мал. ^[112] Линеаризованная теория предсказывает общий характер распределения давления аэродинамического профиля и то, как на него влияют форма аэродинамического профиля и угол атаки, но она недостаточно точна для проектных работ. Для двумерного аэродинамического профиля такие расчеты можно выполнить за доли секунды в электронной таблице на ПК.

Циркуляция и теорема Кутты–Жуковского

Циркуляционная составляющая обтекания аэродинамического профиля

Когда аэродинамический профиль создает подъемную силу, несколько компонентов общего поля скорости способствуют чистой циркуляции воздуха вокруг него: восходящий поток перед аэродинамическим профилем, ускоренный поток сверху, замедленный поток снизу и нисходящий поток сзади.

Циркуляцию можно понимать как общую величину «вращения» (или завихренности ) невязкой жидкости вокруг аэродинамического профиля.

Теорема Кутты-Жуковского связывает подъемную силу на единицу ширины размаха двумерного аэродинамического профиля с этой циркуляционной составляющей потока. ^{[85] [113] [114]} Это ключевой элемент в объяснении подъемной силы, которая следует за развитием потока вокруг аэродинамического профиля, когда аэродинамический профиль начинает свое движение из состояния покоя, и формируется и остается начальный вихрь , что приводит к образованию циркуляции вокруг аэродинамического профиля. ^{[115] [116] [117]} Затем подъемная сила выводится из теоремы Кутты-Жуковского. Это объяснение в значительной степени математическое, и его общая прогрессия основана на логическом выводе, а не на физической причинно-следственной связи. ^[118]

Модель Кутты–Жуковского не предсказывает, какую циркуляцию или подъемную силу создает двумерный аэродинамический профиль. Расчет подъемной силы на единицу размаха с использованием Кутты–Жуковского требует известного значения циркуляции. В частности, если выполняется условие Кутты, при котором задняя точка торможения перемещается к задней кромке аэродинамического профиля и закрепляется там на время полета, подъемную силу можно рассчитать теоретически с помощью метода конформного отображения.

Подъемная сила, создаваемая обычным аэродинамическим профилем, определяется как его конструкцией, так и условиями полета, такими как скорость поступательного движения, угол атаки и плотность воздуха. Подъемную силу можно увеличить путем искусственного увеличения циркуляции, например, путем продувки пограничного слоя или использования продуваемых закрылков . В роторе Флеттнера весь аэродинамический профиль имеет круглую форму и вращается вокруг оси размаха, создавая циркуляцию.

Трехмерный поток

Поперечное сечение крыла самолета, показывающее изобары трехмерного подъемного потока.

Поперечное сечение крыла самолета с корпусом, показывающее векторы скорости трехмерного подъемного потока

Поток вокруг трехмерного крыла включает в себя существенные дополнительные проблемы, особенно связанные с законцовками крыла. Для крыла с малым удлинением , такого как типичное треугольное крыло , двумерные теории могут обеспечить плохую модель, и трехмерные эффекты потока могут доминировать. ^[119] Даже для крыльев с большим удлинением трехмерные эффекты, связанные с конечным размахом, могут влиять на весь размах, а не только вблизи законцовок.

Законцовки крыла и распределение по размаху

Вертикальный градиент давления на концах крыла заставляет воздух течь вбок, из-под крыла, затем вверх и обратно по верхней поверхности. Это уменьшает градиент давления на конце крыла, следовательно, также уменьшает подъемную силу. Подъемная сила имеет тенденцию уменьшаться в направлении размаха от корня к кончику, и распределение давления вокруг секций аэродинамического профиля изменяется соответственно в направлении размаха. Распределение давления в плоскостях, перпендикулярных направлению полета, имеет тенденцию выглядеть как на иллюстрации справа. ^[120] Это изменяющееся по размаху распределение давления поддерживается взаимным взаимодействием с полем скорости. Поток под крылом ускоряется снаружи, поток снаружи кончиков ускоряется вверх, а поток над крылом ускоряется внутри, что приводит к схеме потока, показанной справа. ^[121]

Поток имеет больший поворот вниз, чем это было бы в двумерном потоке с той же формой аэродинамического профиля и секционной подъемной силой, и для достижения той же подъемной силы требуется больший секционный угол атаки по сравнению с двумерным потоком. ^[122] Крыло фактически летит в нисходящем потоке, созданном им самим, как если бы поток свободного потока был наклонен вниз, в результате чего общий вектор аэродинамической силы слегка наклонен назад по сравнению с тем, каким он был бы в двух измерениях. Дополнительный обратный компонент вектора силы называется сопротивлением, вызванным подъемной силой .

Расчет Эйлера концевого вихря, сворачивающегося из отстающей вихревой полосы

Разница в размахе компонента скорости над и под крылом (между нахождением во внутреннем направлении сверху и во внешнем направлении снизу) сохраняется на задней кромке и в следе ниже по потоку. После того, как поток покидает заднюю кромку, эта разница в скорости происходит через относительно тонкий сдвиговой слой, называемый вихревой пеленой.

Система подковообразного вихря

Вид сверху на крыло, демонстрирующий систему подковообразных вихрей.

Поток законцовки крыла, покидающий крыло, создает концевой вихрь. Когда основная вихревая пелена проходит вниз по потоку от задней кромки, она закручивается на своих внешних краях, сливаясь с концевыми вихрями. Сочетание концевых вихрей крыла и питающих их вихревых пелен называется вихревым следом.

В дополнение к вихреобразованию в вихревом следе заднего хода существует вихреобразование в пограничном слое крыла, называемое «связанным вихрем», которое соединяет хвостовые листы с двух сторон крыла в вихревую систему в общей форме подковы. Подковообразная форма вихревой системы была признана британским пионером аэронавтики Ланчестером в 1907 году. ^[123]

Учитывая распределение связанной завихренности и завихренности в следе, закон Био-Савара (соотношение векторного исчисления) может быть использован для расчета возмущения скорости в любой точке поля, вызванного подъемной силой на крыле. Приближенные теории распределения подъемной силы и сопротивления трехмерных крыльев, вызванного подъемной силой, основаны на таком анализе, примененном к системе подковообразных вихрей крыла. ^{[124] [125]} В этих теориях связанная завихренность обычно идеализируется и предполагается, что она находится на поверхности изгиба внутри крыла.

Поскольку в таких теориях скорость выводится из завихренности, некоторые авторы описывают ситуацию так, что завихренность является причиной возмущений скорости, используя такие термины, как, например, «скорость, вызванная вихрем». ^[126] Но приписывание механической причинно-следственной связи между завихренностью и скоростью таким образом не согласуется с физикой. ^{[127] [128] [129]} Возмущения скорости в потоке вокруг крыла на самом деле создаются полем давления. ^[130]

Проявления подъемной силы в дальнем поле

Интегрированный баланс силы/импульса в подъемных потоках

Контрольные объемы различных форм, которые использовались при анализе баланса импульса в 2D-потоке вокруг подъемного аэродинамического профиля. Предполагается, что аэродинамический профиль оказывает направленную вниз силу −L' на единицу размаха на воздух, и пропорции, в которых эта сила проявляется в виде потоков импульса и разностей давления на внешней границе, указаны для каждой различной формы контрольного объема.

Поток вокруг подъемного профиля должен удовлетворять второму закону Ньютона относительно сохранения импульса, как локально в каждой точке поля потока, так и в интегрированном смысле по любой расширенной области потока. Для расширенной области второй закон Ньютона принимает форму теоремы импульса для контрольного объема , где контрольным объемом может быть любая область потока, выбранная для анализа. Теорема импульса утверждает, что интегрированная сила, приложенная на границах контрольного объема ( поверхностный интеграл ), равна интегрированной временной скорости изменения ( материальной производной ) импульса жидких пакетов, проходящих через внутреннюю часть контрольного объема. Для стационарного потока это можно выразить в форме чистого поверхностного интеграла потока импульса через границу. ^[131]

Подъемный поток вокруг 2D-профиля обычно анализируется в контрольном объеме, который полностью окружает профиль, так что внутренняя граница контрольного объема является поверхностью профиля, где направленная вниз сила на единицу размаха прикладывается к жидкости со стороны профиля. Внешняя граница обычно представляет собой либо большой круг, либо большой прямоугольник. На этой внешней границе, удаленной от профиля, скорость и давление хорошо представлены скоростью и давлением, связанными с равномерным потоком плюс вихрь, а вязкое напряжение пренебрежимо мало, так что единственная сила, которая должна быть интегрирована по внешней границе, — это давление. ^{[132] [133] [134]} Скорость свободного потока обычно предполагается горизонтальной, с подъемной силой вертикально вверх, так что вертикальный импульс является интересующим компонентом. ${\displaystyle -L'}$

Для случая свободного воздуха (без плоскости заземления) сила, оказываемая аэродинамическим профилем на жидкость, проявляется частично как потоки импульса и частично как разности давлений на внешней границе, в пропорциях, которые зависят от формы внешней границы, как показано на диаграмме справа. Для плоского горизонтального прямоугольника, который намного длиннее своей высоты, потоки вертикального импульса через переднюю и заднюю части пренебрежимо малы, и подъемная сила полностью учитывается интегрированными разностями давления сверху и снизу. ^[132] Для квадрата или круга потоки импульса и разности давлений составляют половину подъемной силы каждый. ^{[132] [133] [134]} Для вертикального прямоугольника, который намного выше своей ширины, несбалансированные силы давления сверху и снизу незначительны, и подъемная сила полностью объясняется потоками импульса, при этом поток восходящего импульса, который входит в контрольный объем через переднюю часть, составляет половину подъемной силы, а поток нисходящего импульса, который выходит из контрольного объема через заднюю часть, составляет другую половину. ^[132] ${\displaystyle -L'}$

Результаты всех анализов контрольного объема, описанных выше, согласуются с теоремой Кутты–Жуковского, описанной выше. В выводах теоремы использовались как высокие прямоугольные, так и круговые контрольные объемы. ^{[133] [134]}

Подъемная сила отреагировала избыточным давлением на землю под самолетом

Иллюстрация распределения давления, превышающего атмосферное, на земле под самолетом, летящим со скоростью дозвука

Аэродинамический профиль создает поле давления в окружающем воздухе, как объяснено в разделе «Более широкий поток вокруг аэродинамического профиля» выше. Перепады давления, связанные с этим полем, постепенно затухают, становясь очень малыми на больших расстояниях, но никогда не исчезая полностью. Под самолетом поле давления сохраняется как положительное возмущение давления, которое достигает земли, образуя картину немного более высокого, чем окружающее давление на землю, как показано справа. ^[135] Хотя перепады давления очень малы далеко под самолетом, они распределены по большой площади и складываются в существенную силу. Для устойчивого горизонтального полета интегрированная сила, вызванная перепадами давления, равна общей аэродинамической подъемной силе самолета и весу самолета. Согласно третьему закону Ньютона, эта сила давления, оказываемая на землю воздухом, уравновешивается равной и противоположно направленной восходящей силой, оказываемой на воздух землей, которая компенсирует всю нисходящую силу, оказываемую на воздух самолетом. Следовательно, чистая сила, обусловленная подъемной силой, действующей на атмосферу в целом, равна нулю, и, таким образом, в атмосфере не происходит комплексного накопления вертикального импульса, как это было отмечено Ланчестером на раннем этапе развития современной аэродинамики. ^[136]

Смотрите также

• Коэффициент лобового сопротивления
• Разделение потока
• Динамика жидкости
• Фольга (механика жидкости)
• эффект Кюсснера
• Подъемно-лобовое отношение
• Теория подъемной линии
• Спойлер (автомобильный)

Сноски

1. "Что такое Lift?". NASA Glenn Research Center. Архивировано из оригинала 9 февраля 2023 г. Получено 9 февраля 2023 г.
2. Кулфан (2010)
3. Величина аэродинамической подъемной силы (обычно немного) больше или меньше силы тяжести в зависимости от уровня тяги и вертикального выравнивания линии тяги. Боковая линия тяги также приводит к некоторой подъемной силе, противодействующей боковой тяге.
4. Клэнси, Л.Дж., Аэродинамика , Раздел 14.6
5. Дуг Маклин Аэродинамическая подъемная сила, часть 2: всестороннее физическое объяснение Учитель физики, ноябрь 2018 г.
6. Дуг Маклин Аэродинамический подъем, Часть 1: Наука Учитель физики, Ноябрь, 2018
7. "Существует множество теорий о том, как возникает подъемная сила. К сожалению, многие теории, изложенные в энциклопедиях, на веб-сайтах и ​​даже в некоторых учебниках, неверны, что приводит к ненужной путанице среди студентов". NASA "Неправильная теория подъемной силы № 1". 16 августа 2000 г. Архивировано из оригинала 27 апреля 2014 г. Получено 27 июня 2021 г.
8. "В большинстве текстов формула Бернулли представлена ​​без вывода, но также с очень небольшими пояснениями. Применительно к подъемной силе аэродинамического профиля объяснения и диаграммы почти всегда неверны. По крайней мере для вводного курса подъемная сила аэродинамического профиля должна быть объяснена просто в терминах третьего закона Ньютона, при этом тяга вверх должна быть равна скорости изменения импульса воздуха вниз по времени". Клифф Шварц и др. Придирки, недоразумения и вопиющие ошибки – Обзор текстов по физике в старших классах The Physics Teacher Vol. 37, May 1999 p. 300 [1] Архивировано 25 августа 2019 г. на Wayback Machine
9. Arvel Gentry Proceedings of the Third AIAA Symposium on the Aero/Hydronautics of Sailing 1971. "The Aerodynamics of Sail Interaction" (PDF) . Архивировано из оригинала (PDF) 7 июля 2011 г. . Получено 12 июля 2011 г. . Одно из объяснений того, как крыло . . создает подъемную силу, заключается в том, что из-за формы аэродинамического профиля воздух течет быстрее сверху, чем снизу, потому что ему нужно пройти большее расстояние. Конечно, с нашими парусами с тонким аэродинамическим профилем расстояние вдоль верха такое же, как и вдоль низа, поэтому это объяснение подъемной силы не работает.{{cite web}}: CS1 maint: numeric names: authors list (link)
10. "Часто дается объяснение, что путь вдоль верхней стороны аэродинамического профиля длиннее, и воздух, таким образом, должен быть быстрее. Это объяснение неверно". Сравнение объяснений аэродинамической подъемной силы Клаус Вельтнер, Am. J. Phys. Vol.55 1 января 1987 г.
11. "Подъемная сила тела проста... это реакция твердого тела на поворот движущейся жидкости... Теперь, почему жидкость поворачивается так, как она это делает? Вот где вступает в игру сложность, потому что мы имеем дело с жидкостью. ...Причиной поворота потока является одновременное сохранение массы, импульса (как линейного, так и углового) и энергии жидкостью. И это сбивает с толку для жидкости, потому что масса может двигаться и перераспределяться (в отличие от твердого тела), но может делать это только способами, которые сохраняют импульс (масса, умноженная на скорость) и энергию (масса, умноженная на квадрат скорости)... Изменение скорости в одном направлении может вызвать изменение скорости в перпендикулярном направлении в жидкости, чего не происходит в механике твердого тела... Поэтому точное описание того, как поворачивается поток, является сложной проблемой; слишком сложной для большинства людей, чтобы визуализировать это. Поэтому мы составляем упрощенные "модели". А когда мы упрощаем, мы что-то упускаем. Поэтому модель несовершенна. Большинство аргументов о создании подъемной силы сводятся к тому, что люди находят недостатки в различных модели, и поэтому аргументы обычно очень обоснованы». Том Бенсон из Исследовательского центра Гленна НАСА в интервью AlphaTrainer.Com «Архивная копия – Интервью с Томом Бенсоном». Архивировано из оригинала 27 апреля 2012 г. Получено 26 июля 2012 г.
12. Клэнси, Л.Дж., Аэродинамика , Раздел 5.2.
13. Маклин, Дуг (2012). Понимание аэродинамики: аргументация с позиций реальной физики . John Wiley & Sons. стр. 281. ISBN 978-1119967514. Другой часто приводимый аргумент, как в нескольких последовательных версиях статьи Википедии «Аэродинамическая подъемная сила», заключается в том, что подъемную силу всегда можно объяснить либо с точки зрения давления, либо с точки зрения импульса, и что эти два объяснения каким-то образом «эквивалентны». Этот подход «или/или» также не попадает в цель.
14. "Оба подхода одинаково допустимы и одинаково правильны, концепция, которая является центральной для заключения этой статьи". Чарльз Н. Истлейк Взгляд аэродинамика на подъемную силу, Бернулли и Ньютон Учитель физики Том 40, март 2002 г. "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 11 апреля 2009 г. . Получено 10 сентября 2009 г. .{{cite web}}: CS1 maint: archived copy as title (link)
15. Айсон, Дэвид, «Бернулли или Ньютон: кто прав насчет подъемной силы?», Plane & Pilot , заархивировано из оригинала 24 сентября 2015 г. , извлечено 14 января 2011 г.
16. "...эффект крыла заключается в том, чтобы придать воздушному потоку нисходящую составляющую скорости. Сила реакции отклоненной воздушной массы должна затем воздействовать на крыло, чтобы придать ему равную и противоположную восходящую составляющую". В: Halliday, David; Resnick, Robert, Fundamentals of Physics 3rd Ed. , John Wiley & Sons, стр. 378
17. Андерсон и Эберхардт (2001)
18. Лангевише (1944)
19. "Когда воздух течет над и под аэродинамическим профилем, наклоненным под небольшим углом к ​​его направлению, воздух отклоняется от своего курса. Теперь, когда тело движется с постоянной скоростью по прямой линии, требуется сила, чтобы изменить либо его направление, либо скорость. Поэтому паруса оказывают силу на ветер, и, поскольку действие и противодействие равны и противоположны, ветер оказывает силу на паруса". В: Morwood, John, Sailing Aerodynamics , Adlard Coles Limited, стр. 17
20. "Подъемная сила — это сила, создаваемая поворотом движущейся жидкости... Если тело имеет форму, перемещается или наклоняется таким образом, что производит чистое отклонение или поворот потока, локальная скорость изменяется по величине, направлению или по обоим параметрам. Изменение скорости создает чистую силу, действующую на тело". "Подъемная сила от поворота потока". Исследовательский центр имени Гленна в НАСА. 27 мая 2000 г. Архивировано из оригинала 5 июля 2011 г. Получено 27 июня 2021 г.
21. "По сути, из-за наличия крыла (его формы и наклона к набегающему потоку, так называемого угла атаки), поток отклоняется вниз. Здесь действует третий закон Ньютона, при этом поток затем оказывает силу реакции на крыло в направлении вверх, создавая тем самым подъемную силу". Василис Спатопулос – Физика полета для начинающих: Простые примеры применения законов Ньютона Учитель физики Том 49, сентябрь 2011 г., стр. 373 [2]
22. "Главный факт всех полетов тяжелее воздуха заключается в следующем: крыло удерживает самолет в воздухе, толкая воздух вниз ". В: Langewiesche – Stick and Rudder , стр. 6
23. "Птицы и самолеты летают, потому что они постоянно толкают воздух вниз: L = Δp/Δt, где L = подъемная сила, а Δp/Δt — скорость, с которой нисходящий импульс передается воздушному потоку". Полет без Бернулли Крис Уолтем Учитель физики Том 36, ноябрь 1998 г. "Архивная копия" (PDF) . Архивировано (PDF) из оригинала 28 сентября 2011 г. . Получено 4 августа 2011 г. .{{cite web}}: CS1 maint: archived copy as title (link)
24. Клэнси, Л. Дж.; Аэродинамика , Питман 1975, стр. 76: «Эта подъемная сила имеет свою реакцию в виде направленного вниз импульса, который передается воздуху, когда он обтекает крыло. Таким образом, подъемная сила крыла равна скорости переноса направленного вниз импульса этого воздуха».
25. "...если воздух должен создавать восходящую силу на крыле, крыло должно создавать направленную вниз силу на воздухе. Поскольку при этих обстоятельствах воздух не может выдерживать силу, он отклоняется или ускоряется вниз. Второй закон Ньютона дает нам средства для количественной оценки подъемной силы: F _lift = m∆v/∆t = ∆(mv)/∆t. Подъемная сила равна скорости изменения импульса воздуха во времени". Смит, Норман Ф. (1972). "Бернулли и Ньютон в механике жидкости". The Physics Teacher . 10 (8): 451. Bibcode : 1972PhTea..10..451S. doi : 10.1119/1.2352317.
26. "...если учесть нисходящий поток, создаваемый подъемным аэродинамическим профилем, верхняя поверхность вносит больший вклад в поворот потока, чем нижняя поверхность". Неверная теория № 2 Исследовательский центр Гленна НАСА https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/foilw2/ Архивировано 9 февраля 2023 г. на Wayback Machine
27. "Это происходит в некоторой степени как на верхней, так и на нижней поверхности аэродинамического профиля, но это гораздо более выражено на передней части верхней поверхности, поэтому верхняя поверхность получает признание как основной производитель подъемной силы". Чарльз Н. Истлейк Взгляд аэродинамика на подъемную силу, Бернулли и Ньютон Учитель физики Том 40, март 2002 г. PDF Архивировано 11 апреля 2009 г. на Wayback Machine
28. "Давление достигает своего минимального значения примерно на 5–15% хорды после передней кромки. В результате около половины подъемной силы создается в первой 1/4 хорды области аэродинамического профиля. Рассматривая все три угла атаки, мы наблюдаем аналогичное изменение давления после передней кромки. Кроме того, во всех трех случаях верхняя поверхность вносит больший вклад в подъемную силу, чем нижняя поверхность. В результате критически важно поддерживать чистую и жесткую поверхность на верхней части крыла. Вот почему большинство самолетов очищаются от любых предметов на верхней части крыла". Поведение аэродинамического профиля: распределение давления по крылу Clark Y-14 Дэвид Го, Колледж инженерии, технологий и аэронавтики (CETA), Университет Южного Нью-Гемпшира https://www.jove.com/v/10453/airfoil-behavior-pressure-distribution-over-a-clark-y-14-wing Архивировано 5 августа 2021 г. на Wayback Machine
29. «Всегда огромное внимание уделяется верхней части крыла, но нижняя поверхность также вносит свой вклад в подъемную силу». Бернулли или Ньютон: кто прав относительно подъемной силы? Дэвид Айсон Plane & Pilot Февраль 2016 г.
30. Ауэрбах, Дэвид (2000), «Почему самолеты летают», Eur. J. Phys. , 21 (4): 289, Bibcode : 2000EJPh...21..289A, doi : 10.1088/0143-0807/21/4/302, S2CID  250821727
31. Denker, JS, Ошибочная модель производства подъемной силы, архивировано из оригинала 2 марта 2009 г. , извлечено 18 августа 2008 г.
32. Wille, R.; Fernholz, H. (1965), "Отчет о первом европейском коллоквиуме по механике, об эффекте Коанда", J. Fluid Mech. , 23 (4): 801, Bibcode : 1965JFM....23..801W, doi : 10.1017/S0022112065001702, S2CID  121981660
33. Андерсон, Дэвид; Эберхарт, Скотт (1999), Как летают самолеты: физическое описание подъемной силы, архивировано из оригинала 26 января 2016 г. , извлечено 4 июня 2008 г.
34. Раскин, Джеф (1994), Эффект Коанда: понимание того, почему крылья работают, архивировано из оригинала 28 сентября 2007 г.
35. Ауэрбах (2000)
36. Денкер (1996)
37. Вилле и Фернхольц (1965)
38. Уайт, Фрэнк М. (2002), Механика жидкости (5-е изд.), McGraw Hill
39. Маклин, Д. (2012), Раздел 7.3.2
40. Маклин, Д. (2012), Раздел 7.3.1.7
41. Бердж, Сирил Гордон (1936). Энциклопедия авиации. Лондон: Pitman. стр. 441. «… тот факт, что воздух, проходящий через выступ на верхней части крыла, должен ускориться больше, чем тот, который течет под крылом, чтобы достичь задней кромки за то же время».
42. Иллман, Пол (2000). Справочник пилота по аэронавтике. Нью-Йорк: McGraw-Hill. С. 15–16. ISBN 0071345191. «Когда воздух течет вдоль верхней поверхности крыла, он проходит большее расстояние за тот же период времени, что и поток воздуха вдоль нижней поверхности крыла».
43. Дингл, Ллойд; Тули, Майкл Х. (2005). Принципы самолетостроения. Бостон: Elsevier Butterworth-Heinemann. стр. 548. ISBN 0-7506-5015-X. Воздух, проходящий по выпуклой верхней поверхности аэродинамического профиля, показанной на рисунке 7.6, которая разделяется при прохождении вокруг аэродинамического профиля, будет ускоряться, поскольку он должен достичь задней кромки аэродинамического профиля в то же время, что и воздух, который течет под секцией.
44. "Аэродинамический профиль крыла самолета, согласно объяснению из учебника, которое является более или менее стандартным в Соединенных Штатах, имеет особую форму с большей кривизной сверху, чем снизу; следовательно, воздух должен проходить большее расстояние по верхней поверхности, чем по нижней. Поскольку воздух должен пролететь по верхней и нижней поверхностям за одинаковое время..., скорость по верхней поверхности будет больше, чем по нижней. Согласно теореме Бернулли, эта разница скоростей создает разницу давлений, которая является подъемной силой". Бернулли и Ньютон в механике жидкости Норман Ф. Смит, учитель физики , ноябрь 1972 г., том 10, выпуск 8, стр. 451 [3] ^{[ постоянная нерабочая ссылка ]}
45. Крейг ГМ (1997), Хватит ругать Бернулли
46. "К сожалению, это объяснение [не работает] по трем пунктам. Во-первых, у аэродинамического профиля не обязательно должна быть большая кривизна сверху, чем снизу. Самолеты могут летать и летают с идеально симметричными аэродинамическими профилями; то есть с аэродинамическими профилями, имеющими одинаковую кривизну сверху и снизу. Во-вторых, даже если используется горбатая (выпуклая) форма, утверждение о том, что воздух должен пересекать изогнутую верхнюю поверхность за то же время, что и плоскую нижнюю поверхность... является вымышленным. Мы не можем привести ни одного физического закона, который бы говорил нам об этом. В-третьих, и это самое серьезное, общепринятое объяснение в учебниках и сопровождающие его диаграммы описывают силу на крыле без чистого возмущения воздушного потока. Это является нарушением третьего закона Ньютона". Бернулли и Ньютон в механике жидкости Норман Ф. Смит, учитель физики , ноябрь 1972 г., том 10, выпуск 8, стр. 451 "Просмотр - учитель физики". Архивировано из оригинала 17 марта 2012 г. Получено 4 августа 2011 г.
47. Андерсон, Дэвид (2001), Понимание полета , Нью-Йорк: McGraw-Hill, стр. 15, ISBN 978-0-07-136377-8Первое , что неверно, это то, что принцип равного времени прохождения не верен для крыла с подъемной силой.
48. Андерсон, Джон (2005). Введение в полет . Бостон: McGraw-Hill Higher Education. стр. 355. ISBN 978-0072825695. Затем предполагается, что эти два элемента должны встретиться на задней кромке, и поскольку расстояние пробега по верхней поверхности аэродинамического профиля больше, чем по нижней поверхности, элемент по верхней поверхности должен двигаться быстрее. Это просто неверно
49. "Ученый из Кембриджа развенчивает миф о полетах - Telegraph". Архивировано из оригинала 30 июня 2012 г. Получено 10 июня 2012 г. Кембриджский ученый развенчивает миф о полетах UK Telegraph 24 января 2012 г.
50. Визуализация потока. Национальный комитет по фильмам по механике жидкостей/Центр образовательного развития. Архивировано из оригинала 21 октября 2016 г. Получено 21 января 2009 г.Визуализация типичного замедленного потока над нижней поверхностью крыла и ускоренного потока над верхней поверхностью начинается с 5:29 видео.
51. "...помните, как вы слышали эту тревожную историю о частицах, движущихся по изогнутой верхней поверхности, которые должны двигаться быстрее, чем частицы, которые прошли под ней, потому что у них более длинный путь, но они все равно должны попасть туда в то же время? Это просто неправда. Такого не бывает". Чарльз Н. Истлейк Взгляд аэродинамика на подъемную силу, Бернулли и Ньютон Учитель физики Том 40, март 2002 г. PDF Архивировано 11 апреля 2009 г. на Wayback Machine
52. "Фактическая скорость над верхней частью аэродинамического профиля намного выше, чем предсказывает теория "более длинного пути", и частицы, движущиеся над верхней частью, достигают задней кромки раньше, чем частицы, движущиеся под аэродинамическим профилем". Исследовательский центр Гленна (16 августа 2000 г.). "Неправильная теория подъема № 1". NASA. Архивировано из оригинала 27 апреля 2014 г. Получено 27 июня 2021 г.
53. "По мере того, как трубка потока A движется к аэродинамическому профилю, она воспринимает верхнюю часть аэродинамического профиля как препятствие, и трубка потока A должна уйти с пути этого препятствия. При этом трубка потока A сжимается до меньшей площади поперечного сечения, поскольку она протекает по носовой части аэродинамического профиля. В свою очередь, из-за непрерывности массы (ρ AV = константа), скорость потока в трубке потока должна увеличиваться в области, где трубка потока сжимается". JD Anderson (2008), Введение в полет (6-е издание), раздел 5.19
54. "Теория основана на идее, что верхняя поверхность аэродинамического профиля имеет форму, действующую как сопло, которое ускоряет поток. Такая конфигурация сопла называется соплом Вентури, и ее можно проанализировать классически. Учитывая сохранение массы, масса, протекающая мимо любой точки сопла, является постоянной; массовый расход сопла Вентури является постоянной величиной... При постоянной плотности уменьшение площади увеличивает скорость". Неправильная теория № 3 Исследовательский центр Гленна НАСА https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/venturi-theory/ Архивировано 9 февраля 2023 г. на Wayback Machine
55. "Проблема с теорией "Вентури" заключается в том, что она пытается предоставить нам скорость, основанную на неверном предположении (сужение потока создает поле скорости). Мы можем вычислить скорость, основанную на этом предположении, и использовать уравнение Бернулли для вычисления давления, а также выполнить расчет площади давления, и полученный нами ответ не согласуется с подъемной силой, которую мы измеряем для данного профиля". NASA Glenn Research Center "Неправильная теория подъемной силы № 3". 16 августа 2000 г. Архивировано из оригинала 17 июля 2012 г. Получено 27 июня 2021 г.
56. "Концепция... использует симметричный сходящийся-расходящийся канал, как продольный участок трубки Вентури, в качестве отправной точки... когда такое устройство помещается в поток, статическое давление в трубке уменьшается. Когда верхняя половина трубки удаляется, остается геометрия, напоминающая аэродинамический профиль, и всасывание все еще сохраняется наверху. Конечно, это объяснение также некорректно, потому что изменение геометрии влияет на все поле потока, и в описании нет никакой физики, вовлеченной в него". Яакко Хоффрен Поиски улучшенного объяснения подъемной силы Раздел 4.3 Американский институт аэронавтики и астронавтики 2001 "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 7 декабря 2013 г. . Получено 26 июля 2012 г. .{{cite web}}: CS1 maint: archived copy as title (link)
57. "Это дает ответ на кажущуюся загадку того, как симметричный аэродинамический профиль может создавать подъемную силу. ... Это также верно для плоской пластины при ненулевом угле атаки". Чарльз Н. Истлейк, Аэродинамический взгляд на подъемную силу, Бернулли и Ньютон "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 11 апреля 2009 г. Получено 10 сентября 2009 г.{{cite web}}: CS1 maint: archived copy as title (link)
58. "Это классическое объяснение основано на разнице скоростей потока, вызванной аэродинамическим профилем. Однако остается вопрос: как аэродинамический профиль вызывает разницу скоростей потока? Некоторые книги не дают никакого ответа, в то время как другие просто подчеркивают картину линий тока, говоря, что аэродинамический профиль уменьшает разделение линий тока на верхней стороне. Они не говорят, как аэродинамический профиль умудряется это делать. Таким образом, это не является достаточным ответом". Клаус Вельтнер Закон Бернулли и аэродинамическая подъемная сила The Physics Teacher Февраль 1990 г. стр. 84. [4] ^{[ постоянная мертвая ссылка ]}
59. Дуг Маклин Понимание аэродинамики , раздел 7.3.1.5, Wiley, 2012
60. "Нет ничего неправильного в принципе Бернулли или в утверждении, что воздух движется быстрее над верхней частью крыла. Но, как следует из вышеизложенного обсуждения, наше понимание не является полным с этим объяснением. Проблема в том, что мы упускаем важную часть, когда применяем принцип Бернулли. Мы можем рассчитать давление вокруг крыла, если знаем скорость воздуха над и под крылом, но как нам определить скорость?" Как летают самолеты: физическое описание подъемной силы Дэвид Андерсон и Скотт Эберхардт "Как летают самолеты". Архивировано из оригинала 26 января 2016 г. Получено 26 января 2016 г.
61. Равномерное давление, окружающее тело, не создает результирующей силы. (См. плавучесть ). Поэтому для приложения силы к телу, погруженному в жидкость, необходимы перепады давления. Например, см.: Batchelor, GK (1967), An Introduction to Fluid Dynamics , Cambridge University Press, стр. 14–15, ISBN 978-0-521-66396-0
62. " ...если линия тока изогнута, должен быть градиент давления поперек линии тока... " Бабинский, Хольгер (ноябрь 2003 г.), "Как работают крылья?", Physics Education , 38 (6): 497, Bibcode : 2003PhyEd..38..497B, doi : 10.1088/0031-9120/38/6/001, S2CID  1657792
63. Таким образом, создается распределение давления, которое задается в уравнении Эйлера. Физическая причина — аэродинамический профиль, который заставляет линию тока следовать его изогнутой поверхности. Низкое давление на верхней стороне аэродинамического профиля является следствием изогнутой поверхности. Сравнение объяснений аэродинамической подъемной силы Клаус Вельтнер Am. J. Phys. Vol.55 No.January 1, 1987, p. 53 [5] Архивировано 28 апреля 2021 г. на Wayback Machine
64. "Можно утверждать, что основная подъемная сила возникает из-за того, что крыло слегка наклонено вверх, так что воздух, ударяющийся о нижнюю часть крыла, принудительно опускается вниз. Сила реакции третьего закона Ньютона, направленная вверх на крыло, обеспечивает подъемную силу. Увеличение угла атаки может увеличить подъемную силу, но это также увеличивает сопротивление, так что вам придется обеспечивать большую тягу с помощью двигателей самолета" Гиперфизика Университет штата Джорджия Кафедра физики и астрономии "Угол атаки для аэродинамического профиля". Архивировано из оригинала 14 октября 2012 г. Получено 26 июля 2012 г.
65. "Если мы увеличиваем угол атаки, мы увеличиваем отклонение воздушного потока аэродинамическим профилем. Это приводит к увеличению вертикальной составляющей скорости воздушного потока... мы можем ожидать, что подъемная сила линейно зависит от угла атаки. Эта зависимость полностью согласуется с результатами экспериментов..." Клаус Вельтнер Сравнение объяснений аэродинамической подъемной силы Am. J. Phys. 55(1), январь 1987 г., стр. 52
66. "Уменьшение [d lift] углов, превышающих 25°, является правдоподобным. Для больших углов атаки мы получаем турбулентность и, следовательно, меньшее отклонение вниз". Клаус Вельтнер Сравнение объяснений аэродинамической подъемной силы Am. J. Phys. 55(1), январь 1987 г., стр. 52
67. Клэнси (1975), Раздел 5.2
68. Эбботт и фон Денхофф (1958), Раздел 4.2
69. "При угле атаки 0° мы можем объяснить, почему у нас уже есть подъемная сила. Воздушный поток за аэродинамическим профилем следует за задней кромкой. Задняя кромка уже имеет направление вниз, если хорда к средней линии профиля горизонтальна". Клаус Вельтнер Сравнение объяснений аэродинамической подъемной силы Am. J. Phys. 55(1), январь 1987 г., стр. 52
70. "...важная вещь об аэродинамическом профиле... не столько в том, что его верхняя поверхность горбатая, а нижняя почти плоская, а просто в том, что он движется в воздухе под углом. Это также позволяет избежать сложного парадокса, что самолет может летать вверх ногами!" NH Fletcher Mechanics of Flight Physics Education Июль 1975 г. [6]
71. «Это требует корректировки угла атаки, но, как ясно продемонстрировано почти на каждом авиашоу, это можно сделать». Гиперфизика GSU Dept. of Physics and Astronomy [7] Архивировано 8 июля 2012 г. на Wayback Machine
72. Уайт (1991), Раздел 1-4
73. Уайт (1991), Раздел 1-2
74. Anderson (1991), Глава 17
75. Abbott и von Doenhoff (1958), Глава 5
76. Шлихтинг (1979), Глава XXIV
77. Эбботт и Дёнхофф (1958), Глава 8
78. Williamson, CHK; Govardhan, R. (2004), "Вихревые вибрации", Annual Review of Fluid Mechanics , 36 : 413–455, Bibcode : 2004AnRFM..36..413W, doi : 10.1146/annurev.fluid.36.050802.122128, S2CID  58937745
79. Шумер, Б. Мутлу; Фредсё, Йорген (2006), Гидродинамика вокруг цилиндрических структур (пересмотренное издание), World Scientific, стр. 6–13, 42–45 и 50–52, ISBN 978-981-270-039-1
80. Здравкович, ММ (2003), Обтекание круговых цилиндров , т. 2, Oxford University Press, стр. 850–855, ISBN 978-0-19-856561-1
81. Клэнси, Л.Дж., Аэродинамика , Разделы 4.5, 4.6
82. Маклин (2012), Раздел 7.3.3
83. Milne-Thomson (1966), Раздел 1.41
84. Джинсы (1967), Раздел 33.
85. Clancy (1975), Раздел 4.5
86. Милн-Томсон (1966.), Раздел 5.31
87. Маклин 2012, Раздел 7.3.3.7
88. Маклин (2012), Раздел 3.5
89. Маклин 2012, Раздел 7.3.3.9"
90. Маклин 2012, Раздел 7.3.3.9
91. Маклин, Дуг (2012). "7.3.3.12". Понимание аэродинамики: аргументация с позиций реальной физики . John Wiley & Sons. ISBN 978-1119967514.Дуг Маклин, Распространенные заблуждения в аэродинамике на YouTube
92. Андерсон (2008), Раздел 5.7
93. Андерсон, Джон Д. (2004), Введение в полет (5-е изд.), McGraw-Hill, стр. 257, ISBN 978-0-07-282569-5
94. Yoon, Joe (28 декабря 2003 г.), Mach Number & Similarity Parameters, Aerospaceweb.org, архивировано из оригинала 24 февраля 2021 г. , извлечено 11 февраля 2009 г.
95. Бэтчелор (1967), Раздел 1.2
96. Туэйтс (1958), Раздел I.2
97. фон Мизес (1959), Раздел I.1
98. "Анализ потока жидкости обычно представляется студентам-инженерам с точки зрения трех фундаментальных принципов: сохранения массы, сохранения импульса и сохранения энергии". Чарльз Н. Истлейк Взгляд аэродинамика на подъемную силу, Бернулли и Ньютон Учитель физики Том 40, март 2002 г. "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 11 апреля 2009 г. . Получено 10 сентября 2009 г. .{{cite web}}: CS1 maint: archived copy as title (link)
99. Уайт (1991), Глава 1
100. Бэтчелор (1967), Глава 3
101. Арис (1989)
102. Spalart, Philippe R. (2000) Амстердам, Нидерланды. Elsevier Science Publishers.
103. Уайт (1991), Раздел 6-2
104. Шлихтинг (1979), Глава XVIII
105. Андерсон (1995)
106. "...всякий раз, когда поле скорости является безвихревым, его можно выразить как градиент скалярной функции, которую мы называем потенциалом скорости φ: V = ∇φ. Существование потенциала скорости может значительно упростить анализ невязких потоков с помощью теории потенциального потока..." Дуг Маклин Понимание аэродинамики: аргументация с позиций реальной физики стр. 26 Wiley "Continuum Fluid Mechanics and the Navier–Stokes Equations". Понимание аэродинамики . 2012. стр. 13. doi :10.1002/9781118454190.ch3. ISBN 9781118454190.
107. Элементы потенциального потока Калифорнийского государственного университета Лос-Анджелеса "Faculty Web Directory". Архивировано из оригинала 11 ноября 2012 г. Получено 26 июля 2012 г.
108. Бэтчелор (1967), Раздел 2.7
109. Милн-Томсон (1966), Раздел 3.31
110. Клэнси (1975), Раздел 4.8
111. Андерсон (1991), Раздел 4.5
112. Клэнси (1975), Разделы 8.1–8
113. фон Мизес (1959), Раздел VIII.2
114. Андерсон (1991), Раздел 3.15
115. Прандтль и Титдженс (1934)
116. Бэтчелор (1967), Раздел 6.7
117. Джентри (2006)
118. Маклин (2012), Раздел 7.2.1
119. Милн-Томсон (1966), Раздел 12.3
120. Маклин (2012), Раздел 8.1.3
121. Маклин (2012), Раздел 8.1.1
122. Hurt, HH (1965) Аэродинамика для морских летчиков , Рисунок 1.30, NAVWEPS 00-80T-80
123. Ланчестер (1907)
124. Милн-Томсон (1966), Раздел 10.1
125. Клэнси (1975), Раздел 8.9
126. Андерсон (1991), Раздел 5.2
127. Бэтчелор (1967), Раздел 2.4
128. Милн-Томсон (1966), Раздел 9.3
129. Дюран (1932), Раздел III.2
130. Маклин (2012), Раздел 8.1
131. Шапиро (1953), Раздел 1.5, уравнение 1.15
132. Лиссаман (1996), «Подъем в тонких слоях: двумерный случай»
133. Дюран (1932), Разделы BV6, BV7
134. Batchelor (1967), Раздел 6.4, стр. 407
135. Прандтль и Титдженс (1934), Рисунок 150
136. Ланчестер (1907), разделы 5 и 112.

Ссылки

• Эбботт, И. Х.; фон Дёнхофф, А. Э. (1958), Теория сечений крыла , Dover Publications
• Андерсон, ДФ; Эберхардт, С. (2001), Понимание полета , McGraw-Hill
• Андерсон, Дж. Д. (1991), Основы аэродинамики, 2-е изд. , McGraw-Hill
• Андерсон, Дж. Д. (1995), Вычислительная гидродинамика, основы с приложениями , McGraw-Hill, ISBN 978-0-07-113210-7
• Андерсон, JD (1997), История аэродинамики , Cambridge University Press
• Андерсон, Дж. Д. (2004), Введение в полет (5-е изд.), McGraw-Hill, стр. 352–361, §5.19, ISBN 978-0-07-282569-5
• Андерсон, JD (2008), Введение в полет, 6-е издание , McGraw Hill
• Арис, Р. (1989), Векторы, тензоры и основные уравнения механики жидкости , Dover Publications
• Ауэрбах, Д. (2000), «Почему самолеты летают», Eur. J. Phys. , 21 (4): 289–296, Bibcode : 2000EJPh...21..289A, doi : 10.1088/0143-0807/21/4/302, S2CID  250821727
• Бабинский, Х. (2003), «Как работают крылья?», Phys. Educ. , 38 (6): 497, Bibcode : 2003PhyEd..38..497B, doi : 10.1088/0031-9120/38/6/001, S2CID  1657792
• Бэтчелор, Г.К. (1967), Введение в гидродинамику , Cambridge University Press
• Клэнси, Л. Дж. (1975), Аэродинамика , Longman Scientific and Technical
• Крейг, GM (1997), Хватит злоупотреблять Бернулли , Андерсон, Индиана: Regenerative Press
• Дюран, У. Ф., ред. (1932), Аэродинамическая теория, т. 1 , Dover Publications
• Истлейк, CN (2002), «Взгляд аэродинамика на подъемную силу, Бернулли и Ньютон», The Physics Teacher , 40 (3): 166–173, Bibcode : 2002PhTea..40..166E, doi : 10.1119/1.1466553, S2CID  121425815
• Джинс, Дж. (1967), Введение в кинетическую теорию газов , Cambridge University Press
• Кулфан, Б.М. (2010), Палеоаэродинамические исследования, часть I: Эволюция биологического и технического полета , AIAA 2010-154
• Ланчестер, Ф. В. (1907), Аэродинамика , A. Constable and Co.
• Лангевише, В. (1944), «Ручка и руль направления – объяснение искусства летать» , McGraw-Hill
• Лиссаман, PBS (1996), Факты о подъемной силе , AIAA 1996-161
• Марчай, Калифорния (1985), Теория и практика парусного спорта , Патнэм
• Макбит, С. (2006), Аэродинамика гоночных автомобилей , Спаркфорд, Хейнс
• Маклин, Д. (2012), Понимание аэродинамики – аргументация с точки зрения реальной физики , Wiley
• Милн-Томсон, Л. М. (1966), Теоретическая аэродинамика, 4-е изд. , Dover Publications
• Прандтль, Л.; Титдженс, О.Г. (1934), Прикладная гидро- и аэромеханика , Dover Publications
• Раскин, Дж. (1994), Эффект Коанда: понимание того, почему крылья работают, архивировано из оригинала 28 сентября 2007 г.
• Шлихтинг, Х. (1979), Теория пограничного слоя, седьмое издание , McGraw-Hill
• Шапиро, А.Х. (1953), Динамика и термодинамика потока сжимаемой жидкости , Ronald Press Co.
• Смит, Н.Ф. (1972), «Бернулли и Ньютон в механике жидкости», The Physics Teacher , 10 (8): 451, Bibcode : 1972PhTea..10..451S, doi : 10.1119/1.2352317
• Спаларт, Филипп Р. (2000), «Стратегии моделирования и имитации турбулентности», Международный журнал по тепловым и жидкостным потокам , 21 (3): 252, Bibcode : 2000IJHFF..21..252S, doi : 10.1016/S0142-727X(00)00007-2
• Шумер, Б.; Мутлу; Фредсё, Йорген (2006), Гидродинамика вокруг цилиндрических структур (пересмотренное издание){{citation}}: CS1 maint: multiple names: authors list (link)
• Туэйтс, Б., ред. (1958), Несжимаемая аэродинамика , Dover Publications
• Триттон, DJ (1980), Физическая гидродинамика , Ван Ностранд Рейнхольд
• Ван Дайк, М. (1969), «Теория пограничного слоя высшего порядка», Annual Review of Fluid Mechanics , 1 (1): 265–292, Bibcode : 1969AnRFM...1..265D, doi : 10.1146/annurev.fl.01.010169.001405
• фон Мизес, Р. (1959), Теория полета , Dover Publications
• Уолтем, К. (1998), «Полет без Бернулли», The Physics Teacher , 36 (8): 457–462, Bibcode : 1998PhTea..36..457W, doi : 10.1119/1.879927
• Велтнер, К. (1987), "Сравнение объяснений аэродинамической подъемной силы", Am. J. Phys. , 55 (1): 53, Bibcode : 1987AmJPh..55...50W, doi : 10.1119/1.14960
• Уайт, FM (1991), Течение вязкой жидкости, 2-е изд. , McGraw-Hill
• Вилле, Р.; Фернхольц, Х. (1965), «Отчет о первом европейском коллоквиуме по механике, об эффекте Коанда», J. Fluid Mech. , 23 (4): 801–819, Bibcode : 1965JFM....23..801W, doi : 10.1017/s0022112065001702, S2CID  121981660
• Williamson, CHK; Govardhan, R (2004), "Вихревые вибрации", Annual Review of Fluid Mechanics , 36 : 413–455, Bibcode : 2004AnRFM..36..413W, doi : 10.1146/annurev.fluid.36.050802.122128, S2CID  58937745
• Здравкович, ММ (2003), Обтекание круговых цилиндров 2 , Oxford University Press, стр. 850–855, ISBN 978-0-19-856561-1

Дальнейшее чтение

• Введение в полет , Джон Д. Андерсон-младший, McGraw-Hill, ISBN 0-07-299071-6 – Доктор Андерсон является куратором аэродинамики в Национальном музее авиации и космонавтики Смитсоновского института и почетным профессором Мэрилендского университета. 
• Understanding Flight , Дэвид Андерсон и Скотт Эберхардт, McGraw-Hill, ISBN 0-07-136377-7 – Физик и авиационный инженер объясняют полет в нетехнических терминах и специально рассматривают миф о равном времени прохождения. Они приписывают циркуляцию аэродинамического профиля эффекту Коанда, что является спорным. 
• Аэродинамика , Клэнси, Л. Дж. (1975), Раздел 4.8, Pitman Publishing Limited, Лондон ISBN 0-273-01120-0 . 
• Аэродинамика, воздухоплавание и механика полета , Маккормик, Барнс У., (1979), Глава 3, John Wiley & Sons, Inc., Нью-Йорк ISBN 0-471-03032-5 . 
• Fundamentals of Flight , Ричард С. Шевелл, Prentice-Hall International Editions, ISBN 0-13-332917-8 – Это текст для односеместрового курса бакалавриата по машиностроению или авиационной технике. Его разделы по теории полета понятны при наличии поверхностных знаний по исчислению и физике. 
• Крейг, Пол П. (1957). «Наблюдение идеального потенциального потока в сверхтекучей жидкости». Physical Review . 108 (5): 1109–1112. Bibcode : 1957PhRv..108.1109C. doi : 10.1103/PhysRev.108.1109.– Эксперименты в условиях сверхтекучести , приводящие к исчезновению подъемной силы в невязком потоке, поскольку условие Кутты больше не выполняется.
• «Аэродинамика на уровне частиц», Чарльз А. Краммер (2005, переработано в 2012) – Трактовка аэродинамики, подчеркивающая корпускулярную природу воздуха, в отличие от обычно используемого приближения жидкости. arXiv :nlin/0507032
• «Полет без Бернулли» Крис Уолтем Том 36, ноябрь 1998 г. Учитель физики – используя физическую модель, основанную на втором законе Ньютона, автор представляет строгую гидродинамическую трактовку полета. [8] Архивировано 28 сентября 2011 г. на Wayback Machine
• Бернулли, Ньютон и динамический подъем Норман Ф. Смит Школа естественных наук и математики том 73 Часть I: Бернулли, Ньютон и динамический подъем Часть II* Архивировано 17 декабря 2012 г. на archive.today Часть II Бернулли, Ньютон и динамический подъем Часть I* Архивировано 14 декабря 2017 г. на Wayback Machine

Внешние ссылки

• Обсуждение очевидного «конфликта» между различными объяснениями подъемной силы Архивировано 25 июля 2021 г. на Wayback Machine
• Учебное пособие NASA с анимацией, описывающее подъемную силу. Архивировано 9 марта 2009 г. на Wayback Machine.
• NASA FoilSim II 1.5 бета. Симулятор лифта
• Объяснение подъемной силы с помощью анимации потока жидкости вокруг аэродинамического профиля. Архивировано 13 июня 2021 г. на Wayback Machine.
• Трактовка вопроса, почему и как крылья создают подъемную силу, с упором на давление. Архивировано 19 декабря 2006 г. на Wayback Machine.
• Physics of Flight – обзор Архивировано 9 марта 2021 г. на Wayback Machine . Онлайн-статья профессора доктора Клауса Вельтнера
• Как работают крылья? Хольгер Бабински
• Бернулли или Ньютон: кто прав насчет подъемной силы? Архивировано 24 сентября 2015 г. в журнале Wayback Machine Plane and Pilot
• Физика на одну минуту Как на самом деле работает крыло? Архивировано 20 мая 2021 г. на Wayback Machine (видео YouTube)
• Как на самом деле работают крылья, Кембриджский университет. Архивировано 14 июня 2021 г. на Wayback Machine Хольгера Бабинского (ссылка на видео «One Minute Physics How Does a Wing actual work?» на YouTube)
• От вершины до морского дна – поднятый вес как функция высоты и глубины Рольфа Штайнеггера
• Joukowski Transform Interactive WebApp Архивировано 19 октября 2019 г. на Wayback Machine
• Как летают самолеты Архивировано 11 июня 2021 г. на видеопрезентации Wayback Machine на YouTube Кшиштофа Фидковски, доцента кафедры аэрокосмической техники Мичиганского университета