Предельная параллель

Геометрический термин

Две прямые, проходящие через заданную точку P и ограничивающие ее параллельно прямой R.

В нейтральной или абсолютной геометрии , а также в гиперболической геометрии может быть много прямых, параллельных данной прямой, проходящих через точку, не лежащую на прямой ; однако на плоскости две параллели могут быть ближе, чем все остальные (по одной в каждом направлении ). ${\displaystyle l}$ ${\displaystyle P}$ ${\displaystyle R}$ ${\displaystyle l}$ ${\displaystyle R}$

Таким образом, полезно сделать новое определение, касающееся параллелей в нейтральной геометрии. Если существуют ближайшие параллели к данной прямой, они известны как предельная параллель , асимптотическая параллель или хоропараллель (хоро от греч . ὅριον — граница).

Для лучей отношение предельной параллельности является отношением эквивалентности , которое включает в себя отношение эквивалентности быть котерминальными.

Если в гиперболическом треугольнике пары сторон являются предельными параллельными, то треугольник является идеальным треугольником .

Определение

Луч Aa является предельной параллельной прямой Bb , записывается так: ${\displaystyle Aa|||Bb}$

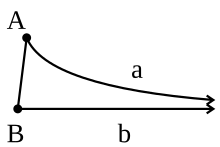
Луч является предельной параллельной лучу, если они котерминальны или лежат на различных прямых, не равных прямой , не пересекаются, и каждый луч внутри угла пересекается с лучом . ^[1] ${\displaystyle Aa}$ ${\displaystyle Bb}$ ${\displaystyle AB}$ ${\displaystyle BAa}$ ${\displaystyle Bb}$

Характеристики

Отдельные линии, несущие предельные параллельные лучи, не встречаются.

Доказательство

Предположим, что линии, несущие различные параллельные лучи, встретились. По определению они не могут встретиться на стороне, на которой находится любой из них . Тогда они должны встретиться на стороне, противоположной , назовем эту точку . Таким образом . Противоречие. ${\displaystyle AB}$ ${\displaystyle a}$ ${\displaystyle AB}$ ${\displaystyle a}$ ${\displaystyle C}$ ${\displaystyle \angle CAB+\angle CBA<2{\text{ right angles}}\Rightarrow \angle aAB+\angle bBA>2{\text{ right angles}}}$

Смотрите также

• орицикл , в гиперболической геометрии кривая , нормали которой являются предельными параллелями
• угол параллельности

Ссылки

1. Хартшорн, Робин (2000). Геометрия: Евклид и далее (исправленное 2-е издание). Нью-Йорк, Нью-Йорк [ua]: Springer. ISBN 978-0-387-98650-0.