Апсидальная прецессия

Вращение линии апсид орбиты небесного тела

Каждая планета, вращающаяся вокруг Солнца , движется по эллиптической орбите , которая постепенно вращается с течением времени (прецессия апсид). Этот рисунок иллюстрирует положительную прецессию апсид (перемещение перигелия), при этом ось орбиты вращается в том же направлении, что и орбитальное движение планеты. Эксцентриситет этого эллипса и скорость прецессии орбиты преувеличены для наглядности. Большинство орбит в Солнечной системе имеют гораздо меньший эксцентриситет и прецессируют с гораздо меньшей скоростью, что делает их почти круговыми и неподвижными .

Основные элементы орбиты (или параметры). Линия апсид показана синим цветом и обозначена ω . Прецессия апсид — это скорость изменения ω во времени, ⁠д ω/д т⁠ .

Анимация орбиты Луны вокруг Земли - Полярный вид
  Луна  ·   Земля

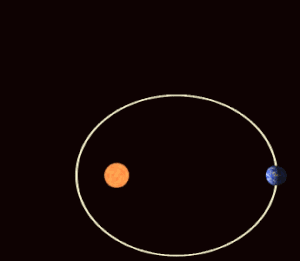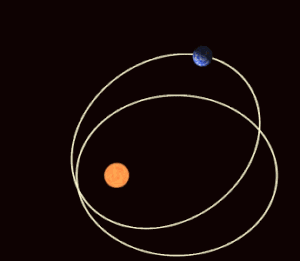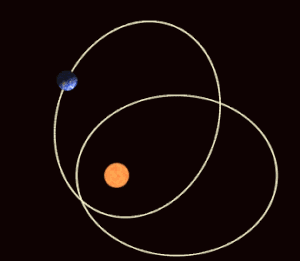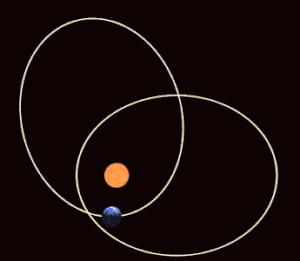
В небесной механике апсидальная прецессия (или апсидальное наступление ) ^[1] — это прецессия (постепенное вращение) линии, соединяющей апсид (линия апсид) орбиты астрономического тела . Апсиды — это орбитальные точки, наиболее удаленные (апоапсис) и наиболее близкие (периапсис) от его основного тела . Апсидальная прецессия — это первая производная по времени аргумента периапсиса , одного из шести основных орбитальных элементов орбиты. Апсидальная прецессия считается положительной, когда ось орбиты вращается в том же направлении, что и орбитальное движение. Апсидальный период — это временной интервал, необходимый для прецессии орбиты на 360°, ^[2] что занимает у Земли около 112 000 лет, а у Луны — около 8,85 лет. ^[3]

История

Древнегреческий астроном Гиппарх отметил апсидальную прецессию орбиты Луны (как оборот апогея Луны с периодом приблизительно 8,85 лет); ^[4] она исправлена ​​в Антикитерском механизме (около 80 г. до н. э.) (с предполагаемым значением 8,88 лет за полный цикл, правильным с точностью до 0,34% от современных измерений). ^[5] Прецессия солнечных апсид (как движение, отличное от прецессии равноденствий) была впервые количественно определена во втором веке Птолемеем Александрийским . Он также вычислил влияние прецессии на движение небесных тел . ^{[6] [7] [8]} Апсидальные прецессии Земли и других планет являются результатом множества явлений, часть из которых оставалась труднообъяснимой до 20-го века, когда была точно объяснена последняя неопознанная часть прецессии Меркурия.

Расчет

К прецессии периастра могут привести различные факторы, такие как общая теория относительности, звездные квадрупольные моменты, взаимные приливные деформации звезды и планеты и возмущения от других планет. ^[9]

ω _всего = ω _{Общая теория относительности} + ω _{квадруполь} + ω _прилив + ω _{возмущения}

Для Меркурия скорость прецессии перигелия из-за общих релятивистских эффектов составляет 43″ ( угловых секунд ) в столетие. Для сравнения, прецессия из-за возмущений от других планет Солнечной системы составляет 532″ в столетие, тогда как сплющенность Солнца (квадрупольный момент) вызывает незначительный вклад в 0,025″ в столетие. ^{[10] [11]}

Согласно классической механике, если звезды и планеты считаются чисто сферическими массами, то они будут подчиняться простому ⁠1/г ²⁠ закон обратных квадратов , связывающий силу с расстоянием и, следовательно, выполняющий замкнутые эллиптические орбиты согласно теореме Бертрана . Несферические массовые эффекты вызваны приложением внешнего потенциала(ов): центробежный потенциал вращающихся тел вызывает сплющивание между полюсами, а гравитация близлежащей массы вызывает приливные выпуклости. Вращательные и чистые приливные выпуклости создают гравитационные квадрупольные поля ( ⁠1/г ³⁠ ), которые приводят к орбитальной прецессии.

Полная прецессия линии апсид для изолированных очень горячих Юпитеров , учитывая только эффекты низшего порядка и в целом в порядке важности,

ω _всего = ω _{приливных возмущений} + ω _{Общая теория относительности} + ω _{вращательных возмущений} + ω _{вращательных *} + ω _{приливных *}

с планетарным приливным выступом, являющимся доминирующим термином, превышающим эффекты общей теории относительности и звездного квадруполя более чем на порядок. Хорошее полученное приближение приливного выступов полезно для понимания внутренностей таких планет. Для планет с самым коротким периодом планетарная внутренность вызывает прецессию в несколько градусов в год. Она составляет до 19,9° в год для WASP-12b . ^{[12] [13]}

Теорема Ньютона о вращающихся орбитах

Ньютон вывел раннюю теорему, которая пыталась объяснить прецессию линии апсид. Эта теорема исторически примечательна, но она никогда широко не использовалась, и она предлагала силы, которые, как было обнаружено, не существуют, что делало теорему недействительной. Эта теорема о вращающихся орбитах оставалась в значительной степени неизвестной и неразвитой в течение более трех столетий до 1995 года. ^[14] Ньютон предположил, что изменения в угловом движении частицы могут быть учтены путем добавления силы, которая изменяется как обратный куб расстояния, не влияя на радиальное движение частицы. ^[15] Используя предшественника ряда Тейлора , Ньютон обобщил свою теорему на все законы сил при условии, что отклонения от круговых орбит малы, что справедливо для большинства планет в Солнечной системе. ^{[ требуется ссылка ]} Однако его теорема не учитывала прецессию линии апсид Луны, не отказываясь от закона обратных квадратов закона всемирного тяготения Ньютона . Кроме того, скорость прецессии линии апсид, рассчитанная с помощью теоремы Ньютона о вращающихся орбитах, не так точна, как для более новых методов, таких как теория возмущений . ^{[ необходима ссылка ]}

изменение орбиты с течением времени

Общая теория относительности

Прецессия апсид планеты Меркурий была отмечена Урбеном Леверье в середине XIX века и объяснена общей теорией относительности Эйнштейна .

В 1910-х годах несколько астрономов вычислили прецессию перигелия согласно специальной теории относительности. Обычно они получали значение, которое составляло всего 1/6 от правильного значения, 7''/год. ^{[16] [17]}

Эйнштейн показал, что для планеты, большая полуось ее орбиты которой равна a , эксцентриситет орбиты e и период обращения T , прецессия линии апсид, вызванная релятивистскими эффектами, за один период обращения в радианах равна

${\displaystyle \varepsilon =24\pi ^{3}{\frac {a^{2}}{T^{2}c^{2}\left(1-e^{2}\right)}}}$

где c — скорость света . ^[18] В случае Меркурия половина большей оси составляет около5,79 × 10 ¹⁰  м , эксцентриситет орбиты равен 0,206, а период обращения равен 87,97 дня или7,6 × 10 ⁶  с . Из них и скорости света (которая составляет ~3 × 10 ⁸  м/с ), можно рассчитать, что прецессия линии апсид за один период обращения составляет ε = 5,028 × 10−7 радиан ⁽2,88 × 10−5 градусов или 0,104″). За сто лет Меркурий совершает примерно 415 оборотов вокруг Солнца, и, таким образом, за это время апсидальный перигелий из-за релятивистских эффектов составляет приблизительно 43″, что почти ^точно соответствует ранее необъясненной части измеренного значения.

Долгосрочный климат

Прецессия апсид Земли медленно увеличивает аргумент перицентра ; это занимает около112 000 лет требуется эллипсу, чтобы совершить один оборот относительно неподвижных звезд. ^[19] Полярная ось Земли, а следовательно, и солнцестояния и равноденствия, прецессируют с периодом около26 000 лет по отношению к неподвижным звездам. Эти две формы «прецессии» объединяются так, что она занимает от20 800 и 29 000 лет (и в среднем23 000 лет) для того, чтобы эллипс совершил один оборот относительно весеннего равноденствия, то есть для того, чтобы перигелий вернулся в ту же дату (при условии, что календарь идеально отслеживает времена года). ^[20]

Это взаимодействие между аномальным и тропическим циклом важно для долгосрочных климатических изменений на Земле, называемых циклами Миланковича . Циклы Миланковича играют центральную роль в понимании эффектов прецессии апсид. Эквивалент также известен на Марсе .

Влияние прецессии апсид на времена года с эксцентриситетом и ап/перигелием на орбите, преувеличенными для удобства просмотра. Показанные времена года относятся к северному полушарию, а в южном полушарии в любой момент времени на орбите времена года будут обратными. Некоторые климатические эффекты следуют в основном из-за преобладания большего количества океанов в Южном полушарии.

Рисунок справа иллюстрирует влияние прецессии на сезоны северного полушария относительно перигелия и афелия. Обратите внимание, что площади, охваченные в течение определенного сезона, меняются со временем. Орбитальная механика требует, чтобы продолжительность сезонов была пропорциональна охваченным площадям сезонных квадрантов, поэтому, когда эксцентриситет орбиты экстремальн, сезоны на дальней стороне орбиты могут быть существенно длиннее.

Смотрите также

• Аксиальная прецессия
• Узловая прецессия
• Гипотрохоидный
• Розетта (орбита)
• Спирограф

Примечания

1. Боулер, МГ (2010). «Апсидальное продвижение в SS 433?». Астрономия и астрофизика . 510 (1): A28. arXiv : 0910.3536 . Bibcode : 2010A&A...510A..28B. doi : 10.1051/0004-6361/200913471. S2CID  119289498.
2. Хилдич, РВ (2001). Введение в тесные двойные звезды. Серия Кембриджских астрофизических издательств. Издательство Кембриджского университета. стр. 132. ISBN 9780521798006.
3. Buis, Alan; Laboratory, s Jet Propulsion (27 февраля 2020 г.). «Milankovitch (Orbital) Cycles and Their Role in Earth's Climate – Climate Change: Vital Signs of the Planet». Climate Change: Vital Signs of the Planet . Получено 2 июня 2023 г.
4. Джонс, А., Александр (сентябрь 1991 г.). «Адаптация вавилонских методов в греческой числовой астрономии» (PDF) . Isis . 82 (3): 440–453. Bibcode :1991Isis...82..441J. doi :10.1086/355836. S2CID  92988054. Архивировано из оригинала (PDF) 4 марта 2016 г. Получено 7 августа 2014 г.
5. Freeth, Tony; Bitsakis, Yanis; Moussas, Xenophon; Seiradakis, John. H.; Tselikas, A.; Mangou, H.; Zafeiropoulou, M.; Hadland, R.; et al. (30 ноября 2006 г.). «Расшифровка древнегреческого астрономического калькулятора, известного как Антикитерский механизм» (PDF) . Nature . 444 Supplement (7119): 587–91. Bibcode :2006Natur.444..587F. doi :10.1038/nature05357. PMID  17136087. S2CID  4424998. Архивировано из оригинала (PDF) 20 июля 2015 г. . Получено 20 мая 2014 г. .
6. Тумер, Г. Дж. (1969), «Солнечная теория аз-Заркала: история ошибок», Centaurus , 14 (1): 306–336, Bibcode : 1969Cent...14..306T, doi : 10.1111/j.1600-0498.1969.tb00146.x, на стр. 314–317.
7. "Птолемеевская астрономия в средние века". princeton.edu . Получено 21 октября 2022 г. .
8. C. Philipp E. Nothaft (2017). «Критика моделей трепидации и защита равномерной прецессии в средневековой латинской астрономии». Архив для History of Exact Sciences . 71 (3): 211–244. doi :10.1007/s00407-016-0184-1. S2CID  253894382.
9. Дэвид М. Киппинг (8 августа 2011 г.). Транзиты внесолнечных планет со спутниками. Springer. стр. 84–. ISBN 978-3-642-22269-6. Получено 27 августа 2013 г.
10. Кейн, SR; Хорнер, J.; фон Браун, K. (2012). «Вероятности циклического транзита долгопериодических эксцентрических планет из-за прецессии периастра». The Astrophysical Journal . 757 (1): 105. arXiv : 1208.4115 . Bibcode :2012ApJ...757..105K. doi :10.1088/0004-637x/757/1/105. S2CID  54193207.
11. Ричард Фицпатрик (30 июня 2012 г.). Введение в небесную механику. Cambridge University Press . стр. 69. ISBN 978-1-107-02381-9. Получено 26 августа 2013 г.
12. Ragozzine, D.; Wolf, AS (2009). «Исследование внутренностей очень горячих юпитеров с использованием транзитных кривых блеска». The Astrophysical Journal . 698 (2): 1778–1794. arXiv : 0807.2856 . Bibcode : 2009ApJ...698.1778R. doi : 10.1088/0004-637x/698/2/1778. S2CID  29915528.
13. Майкл Перриман (26 мая 2011 г.). Справочник по экзопланетам. Cambridge University Press. стр. 133–. ISBN 978-1-139-49851-7. Получено 26 августа 2013 г.
14. Чандрасекар, стр. 183.
15. Линден-Белл, Д.; Джин, С. (1 мая 2008 г.). «Аналитические центральные орбиты и их группа преобразований». Monthly Notices of the Royal Astronomical Society . 386 (1): 245–260. arXiv : 0711.3491 . Bibcode : 2008MNRAS.386..245L. doi : 10.1111/j.1365-2966.2008.13018.x . ISSN  0035-8711. S2CID  15451037.
16. Макдональд, Кирк Т. «Специальная теория относительности и прецессия перигелия». JH Lab., Принстонский университет (2023).
17. Голдштейн, Герберт; Пул, Чарльз П.; Сафко, Джон Л. (2008). Классическая механика (3-е изд., [Nachdr.] изд.). Сан-Франциско Мюнхен: Addison Wesley. Глава 7, Упражнение 27, Страница 332. ISBN 978-0-201-65702-9.
18. Хокинг, Стивен (2002). На плечах гигантов: Великие труды физики и астрономии. Филадельфия, Пенсильвания, США: Running Press . стр. der Physik. ISBN 0-7624-1348-4.
19. van den Heuvel, EPJ (1966). «О прецессии как причине плейстоценовых вариаций температур воды Атлантического океана». Geophysical Journal International . 11 (3): 323–336. Bibcode : 1966GeoJ...11..323V. doi : 10.1111/j.1365-246X.1966.tb03086.x .
20. Времена года и орбита Земли, Военно-морская обсерватория США , архивировано из оригинала 2 августа 2013 г. , извлечено 16 августа 2013 г.