Приливная сила

Гравитационный эффект, также известный как дифференциальная сила и возмущающая сила

Рисунок 1: Приливное взаимодействие между спиральной галактикой NGC 169 и меньшим компаньоном ^[1]

Приливная сила или сила, порождающая приливы, представляет собой гравитационный эффект, который растягивает тело вдоль линии по направлению к центру масс другого тела и от него из-за пространственных изменений напряженности гравитационного поля другого тела. Она отвечает за приливы и связанные с ними явления, включая приливы твердой Земли , приливное запирание , разрыв небесных тел и образование кольцевых систем в пределах предела Роша , а в крайних случаях — спагеттификацию объектов. Она возникает из-за того, что гравитационное поле, оказываемое на одно тело другим, не является постоянным по всем его частям: ближняя сторона притягивается сильнее, чем дальняя. Разница положительна на ближней стороне и отрицательна на дальней стороне, что заставляет тело растягиваться. Таким образом, приливная сила также известна как дифференциальная сила, остаточная сила или вторичный эффект гравитационного поля.

В небесной механике выражение приливная сила может относиться к ситуации, в которой тело или материал (например, приливная вода) находится в основном под гравитационным влиянием второго тела (например, Земли), но также возмущается гравитационным воздействием третьего тела (например, Луны). Возмущающая сила иногда в таких случаях называется приливной силой ^[2] (например, возмущающая сила на Луне ): это разность между силой, оказываемой третьим телом на второе, и силой, оказываемой третьим телом на первое. ^[3]

Было также показано, что приливные силы по сути своей связаны с гравитационными волнами . ^[4]

Объяснение

Рисунок 2: Показанное красным цветом, гравитационное поле Луны на поверхности Земли известно (наряду с другим и более слабым дифференциальным эффектом, вызванным Солнцем) как сила, генерирующая приливы . Это основной механизм, управляющий приливным действием, объясняющий два одновременных приливных выступа.

Вращение Земли также объясняет возникновение двух приливов в день в одном и том же месте. На этом рисунке Земля представляет собой центральный черный круг, в то время как Луна находится далеко справа. Он показывает как приливное поле (толстые красные стрелки), так и гравитационное поле (тонкие синие стрелки), оказываемое на поверхность Земли и центр (метка O) Луной (метка S). Внешнее направление стрелок справа и слева от Земли указывает, где Луна находится в зените или в надире .

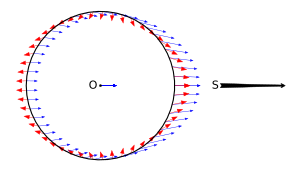
Когда на тело (тело 1) действует сила тяжести другого тела (тело 2), поле может значительно различаться на теле 1 между стороной тела, обращенной к телу 2, и стороной, обращенной от тела 2. На рисунке 2 показана дифференциальная сила тяжести, действующая на сферическое тело (тело 1) со стороны другого тела (тело 2).

Эти приливные силы вызывают деформации обоих тел и могут деформировать их или даже, в крайних случаях, разорвать одно или другое на части. ^[5] Предел Роша — это расстояние от планеты, на котором приливные эффекты могут привести к распаду объекта, поскольку дифференциальная сила гравитации планеты преодолевает притяжение частей объекта друг к другу. ^[6] Эти деформации не возникли бы, если бы гравитационное поле было однородным, поскольку однородное поле заставляет все тело ускоряться вместе в одном направлении и с одинаковой скоростью.

Размер и расстояние

Соотношение размера астрономического тела и его расстояния от другого тела сильно влияет на величину приливной силы. ^[7] Приливная сила, действующая на астрономическое тело, такое как Земля, прямо пропорциональна диаметру Земли и обратно пропорциональна кубу расстояния от другого тела, создающего гравитационное притяжение, такого как Луна или Солнце. Приливное воздействие на ванны, бассейны, озера и другие небольшие водоемы пренебрежимо мало. ^[8]

Рисунок 3: График, показывающий, как гравитационное притяжение уменьшается с увеличением расстояния от тела.

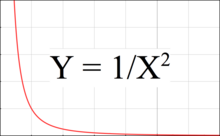
Рисунок 3 представляет собой график, показывающий, как сила тяготения уменьшается с расстоянием. На этом графике сила притяжения уменьшается пропорционально квадрату расстояния ( Y = 1/ X ² ), тогда как наклон ( Y ′ = −2/ X ³ ) обратно пропорционален кубу расстояния.

Приливная сила соответствует разнице Y между двумя точками на графике, одна из которых находится на ближней стороне тела, а другая — на дальней. Приливная сила становится больше, когда две точки находятся либо дальше друг от друга, либо когда они находятся левее на графике, то есть ближе к притягивающему телу.

Например, даже несмотря на то, что Солнце оказывает более сильное гравитационное воздействие на Землю, Луна создает большую приливную выпуклость, поскольку Луна находится ближе. Эта разница обусловлена ​​тем, как гравитация ослабевает с расстоянием: более близкое расположение Луны создает более резкое падение ее гравитационного притяжения по мере вашего перемещения по Земле (по сравнению с очень постепенным падением Солнца из-за его огромного расстояния). Этот более крутой градиент притяжения Луны приводит к большей разнице в силе между ближней и дальней сторонами Земли, что и создает большую приливную выпуклость.

Гравитационное притяжение обратно пропорционально квадрату расстояния от источника. Притяжение будет сильнее на стороне тела, обращенной к источнику, и слабее на стороне, удаленной от источника. Приливная сила пропорциональна разнице. ^[8]

Солнце, Земля и Луна

Земля в 81 раз массивнее Луны, радиус Земли примерно в 4 раза больше радиуса Луны. В результате, на том же расстоянии, приливная сила Земли на поверхности Луны примерно в 20 раз сильнее, чем у Луны на поверхности Земли. ^[9]

Эффекты

Рисунок 4: Кольца Сатурна находятся внутри орбит его главных лун. Приливные силы противостоят гравитационному слиянию материала в кольцах, образуя луны. ^[11]

В случае бесконечно малой упругой сферы эффект приливной силы заключается в искажении формы тела без изменения объема. Сфера становится эллипсоидом с двумя выпуклостями, направленными к другому телу и от него. Более крупные объекты деформируются в овоид и слегка сжимаются, что и происходит с океанами Земли под действием Луны. Все части Земли подвержены гравитационным силам Луны, заставляя воду в океанах перераспределяться, образуя выпуклости по сторонам вблизи Луны и вдали от Луны. ^[12]

Когда тело вращается под действием приливных сил, внутреннее трение приводит к постепенному рассеиванию его вращательной кинетической энергии в виде тепла. В случае Земли и Луны Земли потеря вращательной кинетической энергии приводит к выигрышу около 2 миллисекунд за столетие. Если тело находится достаточно близко к своей основной планете, это может привести к вращению, которое приливно заблокировано орбитальным движением, как в случае Луны Земли. Приливной нагрев вызывает драматические вулканические эффекты на луне Юпитера Ио .Напряжения , вызванные приливными силами, также вызывают регулярные ежемесячные лунотрясения на Луне. ^[7]

Приливные силы способствуют возникновению океанских течений, которые смягчают глобальные температуры, перенося тепловую энергию к полюсам. Было высказано предположение, что изменения приливных сил коррелируют с холодными периодами в глобальной температурной записи с интервалом от 6 до 10 лет ^[13] и что гармонические колебания приливного воздействия могут способствовать тысячелетним изменениям климата. На сегодняшний день не обнаружено прочной связи с тысячелетними изменениями климата. ^[14]

Рисунок 5: Комета Шумейкеров-Леви 9 в 1994 году после распада под воздействием приливных сил Юпитера во время предыдущего прохода в 1992 году.

Приливные эффекты становятся особенно выраженными вблизи небольших тел большой массы, таких как нейтронные звезды или черные дыры , где они ответственны за « спагеттификацию » падающего вещества. Приливные силы создают океанический прилив земных океанов, где притягивающими телами являются Луна и, в меньшей степени, Солнце . Приливные силы также ответственны за приливное запирание , приливное ускорение и приливной нагрев. Приливы также могут вызывать сейсмичность .

Создавая проводящие жидкости внутри Земли, приливные силы также влияют на магнитное поле Земли . ^[15]

Рисунок 6: Эта симуляция показывает, как звезда разрывается на части гравитационными приливами сверхмассивной черной дыры .

Формулировка

Рисунок 7: Приливная сила ответственна за слияние пары галактик MRK 1034. [ ^16]

Рисунок 8: График приливных сил. Верхний рисунок показывает гравитационное поле тела справа (не показано); нижний показывает их остаточную гравитацию после вычитания поля в центре сферы; это приливная сила. Для наглядности верхние стрелки можно считать равными 1 Н, 2 Н и 3 Н (слева направо); полученные нижние стрелки будут равны соответственно -1 Н (отрицательно, поэтому повернуты на 180 градусов), 0 Н (невидимы) и 1 Н. См. рисунок 2 для более подробной версии

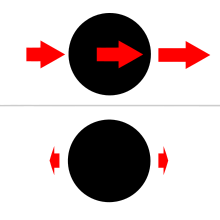
Для данного (внешне созданного) гравитационного поля приливное ускорение в точке относительно тела получается путем векторного вычитания гравитационного ускорения в центре тела (из-за данного внешне созданного поля) из гравитационного ускорения (из-за того же поля) в данной точке. Соответственно, термин приливная сила используется для описания сил, вызванных приливным ускорением. Обратите внимание, что для этих целей единственным рассматриваемым гравитационным полем является внешнее; гравитационное поле тела (как показано на графике) не имеет значения. (Другими словами, сравнение проводится с условиями в данной точке, какими они были бы, если бы не было внешне созданного поля, действующего неравномерно в данной точке и в центре тела отсчета. Внешне созданное поле обычно создается возмущающим третьим телом, часто Солнцем или Луной в частых примерах случаев точек на поверхности Земли или над ней в геоцентрической системе отсчета.)

Приливное ускорение не требует вращения или движения тел по орбите; например, тело может свободно падать по прямой линии под воздействием гравитационного поля, при этом на него по-прежнему влияет (изменяющееся) приливное ускорение.

По закону всемирного тяготения Ньютона и законам движения тело массой m на расстоянии R от центра сферы массой M испытывает силу , ${\displaystyle {\vec {F}}_{g}}$

${\displaystyle {\vec {F}}_{g}=-{\hat {r}}~G~{\frac {Mm}{R^{2}}}}$

эквивалентно ускорению , ${\displaystyle {\vec {a}}_{g}}$

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}}$

где — единичный вектор , направленный от тела М к телу m (здесь ускорение от m к М имеет отрицательный знак). ${\displaystyle {\hat {r}}}$

Рассмотрим теперь ускорение, вызванное сферой массы M, испытываемое частицей вблизи тела массой m . При R как расстоянии от центра M до центра m пусть ∆ r будет (относительно небольшим) расстоянием частицы от центра тела массой m . Для простоты расстояния сначала рассматриваются только в направлении, указывающем к или от сферы массы M. Если тело массой m само является сферой радиуса ∆ r , то новая рассматриваемая частица может быть расположена на ее поверхности на расстоянии ( R ± ∆r ) от центра сферы массы M , и ∆r может быть принято как положительное, когда расстояние частицы от M больше, чем R. Оставляя в стороне любое гравитационное ускорение, которое может испытывать частица по отношению к m из-за собственной массы m , мы имеем ускорение частицы из-за силы гравитации по отношению к M как:

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}}$

Вынося член R2 из знаменателя, получаем ^:

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}~{\frac {1}{\left(1\pm {\frac {\Delta r}{R}}\right)^{2}}}}$

Ряд Маклорена — это ряд, который дает расширение ряда: ${\displaystyle 1/(1\pm x)^{2}}$ ${\displaystyle 1\mp 2x+3x^{2}\mp \cdots }$

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}\pm {\hat {r}}~G~{\frac {2M}{R^{2}}}~{\frac {\Delta r}{R}}+\cdots }$

Первый член — это гравитационное ускорение, вызванное M в центре тела отсчета , т. е. в точке, где равно нулю. Этот член не влияет на наблюдаемое ускорение частиц на поверхности m , поскольку по отношению к M , m (и все на его поверхности) находится в свободном падении. Когда сила, действующая на дальнюю частицу, вычитается из силы, действующей на ближнюю частицу, этот первый член отменяется, как и все другие члены четного порядка. Оставшиеся (остаточные) члены представляют собой разницу, упомянутую выше, и являются членами приливной силы (ускорения). Когда ∆ r мало по сравнению с R , члены после первого остаточного члена очень малы и ими можно пренебречь, что дает приблизительное приливное ускорение для рассматриваемых расстояний ∆ r вдоль оси, соединяющей центры m и M : ${\displaystyle m}$ ${\displaystyle \Delta r}$ ${\displaystyle {\vec {a}}_{t,{\text{axial}}}}$

${\displaystyle {\vec {a}}_{t,{\text{axial}}}\approx \pm {\hat {r}}~2\Delta r~G~{\frac {M}{R^{3}}}}$

При расчете таким образом для случая, когда ∆ r — расстояние вдоль оси, соединяющей центры m и M , направлено наружу от к центру m (где ∆ r равно нулю). ${\displaystyle {\vec {a}}_{t}}$

Приливные ускорения также могут быть рассчитаны вдали от оси, соединяющей тела m и M , требуя векторного расчета. В плоскости, перпендикулярной этой оси, приливное ускорение направлено внутрь (к центру, где ∆ r равно нулю), а его величина находится в линейном приближении, как на рисунке 2. ${\textstyle {\frac {1}{2}}\left|{\vec {a}}_{t,{\text{axial}}}\right|}$

Приливные ускорения на поверхности планет Солнечной системы, как правило, очень малы. Например, лунное приливное ускорение на поверхности Земли вдоль оси Луна-Земля составляет около1,1 × 10−7 г , тогда как ^{солнечное}  приливное ускорение на поверхности Земли вдоль оси Солнце–Земля составляет около0,52 × 10−7 g  , где g — ускорение свободного падения на поверхности Земли. Следовательно, приливная сила (ускорение), вызванная Солнцем, составляет около 45% от силы, вызванной Луной. ^[17] Солнечное приливное ускорение на поверхности Земли было впервые дано Ньютоном в ^« Началах» . ^[18]

Смотрите также

• Амфидромическая точка
• Разрушенная планета
• Галактический прилив
• Приливной резонанс
• Приливно-отливная зачистка
• Приливной тензор
• Искривление пространства-времени

Ссылки

1. «Hubble Views a Cosmic Interaction». nasa.gov . NASA. 11 февраля 2022 г. Получено 09.07.2022 г.
2. «О приливной силе», И. Н. Авсюк, в «Советских астрономических письмах», т. 3 (1977), стр. 96–99.
3. См. стр. 509 в «Астрономия: физическая перспектива», М. Л. Катнер (2003).
4. arXiv, Новые технологии из (2019-12-14). «Приливные силы несут математическую сигнатуру гравитационных волн». MIT Technology Review . Получено 2023-11-12 .
5. Р. Пенроуз (1999). Новый разум императора: о компьютерах, разуме и законах физики . Oxford University Press . стр. 264. ISBN 978-0-19-286198-6. приливная сила.
6. Тереза ​​Энкрена ; Ж-П Бибринг; М Блан (2003). Солнечная система. Спрингер. п. 16. ISBN 978-3-540-00241-3.
7. "Приливная сила | Нил Деграсс Тайсон". www.haydenplanetarium.org . Получено 10 октября 2016 г.
8. Sawicki, Mikolaj (1999). «Мифы о гравитации и приливах». The Physics Teacher . 37 (7): 438–441. Bibcode : 1999PhTea..37..438S. CiteSeerX 10.1.1.695.8981 . doi : 10.1119/1.880345. ISSN  0031-921X. 
9. Шутц, Бернард (2003). Гравитация с нуля: Вводное руководство по гравитации и общей теории относительности (иллюстрированное издание). Cambridge University Press. стр. 45. ISBN 978-0-521-45506-0.Выдержка из страницы 45
10. "2022 CODATA Value: Ньютоновская постоянная тяготения". Справочник NIST по константам, единицам и неопределенности . NIST . Май 2024. Получено 2024-05-18 .
11. RS MacKay; JD Meiss (1987). Гамильтоновы динамические системы: выборка переиздания. CRC Press . стр. 36. ISBN 978-0-85274-205-1.
12. Роллин А. Харрис (1920). Энциклопедия Американа: Библиотека универсальных знаний. Т. 26. Encyclopedia Americana Corp., стр. 611–617.
13. Килинг, CD; Уорф, TP (5 августа 1997 г.). «Возможное воздействие океанических приливов на глобальную температуру». Труды Национальной академии наук . 94 (16): 8321–8328. Bibcode : 1997PNAS...94.8321K. doi : 10.1073/pnas.94.16.8321 . PMC 33744. PMID  11607740 . 
14. Манк, Уолтер; Дзечух, Мэтью; Джейн, Стивен (февраль 2002 г.). «Изменчивость климата в течение тысячелетия: есть ли приливная связь?». Журнал климата . 15 (4): 370–385. Bibcode :2002JCli...15..370M. doi : 10.1175/1520-0442(2002)015<0370:MCVITA>2.0.CO;2 .
15. "Hungry for Power in Space". New Scientist . 123 : 52. 23 сентября 1989 г. Получено 14 марта 2016 г.
16. "Неразлучные галактические близнецы". ESA/Hubble Picture of the Week . Получено 12 июля 2013 г.
17. Адмиралтейство (1987). Руководство по навигации Адмиралтейства. Том 1. Канцелярия . С. 277. ISBN 978-0-11-772880-6., Глава 11, стр. 277
18. Ньютон, Исаак (1729). Математические начала натуральной философии. Т. 2. С. 307. ISBN 978-0-11-772880-6., Книга 3, Предложение 36, Страница 307 Ньютон оценил силу, опускающую море в местах, удаленных на 90 градусов от Солнца, в «1 к 38604600» (в единицах g ), и написал, что сила, поднимающая море вдоль оси Солнце-Земля, «в два раза больше» (т. е. 2 к 38604600), что составляет около 0,52 × 10−7 ^g , как указано в тексте.

Внешние ссылки

• Анализ и прогнозирование приливов: GeoTide
• Гравитационные приливы, автор Дж. Кристофер Михос из Университета Кейс Вестерн Резерв
• Аудио: Cain/Gay – Astronomy Cast Tidal Forces – июль 2007 г.
• Грей, Меган; Меррифилд, Майкл. «Приливные силы». Шестьдесят символов . Брэди Харан для Ноттингемского университета .
• Пау Амаро Сеоане. "Звездные столкновения: приливное разрушение звезды массивной черной дырой" . Получено 28.12.2018 .
• «Мифы о гравитации и приливах» Николая Савицкого из колледжа Джона А. Логана и Университета Колорадо.
• Заблуждения о приливах Дональда Э. Симанека
• Приливы и центробежная сила Паоло Сиртоли