Ячейка Вигнера-Зейтца , названная в честь Юджина Вигнера и Фредерика Зейтца , является примитивной ячейкой , которая была построена путем применения разложения Вороного к кристаллической решетке . Она используется при изучении кристаллических материалов в кристаллографии .

Уникальным свойством кристалла является то, что его атомы расположены в регулярном трехмерном массиве, называемом решеткой . Все свойства, приписываемые кристаллическим материалам, вытекают из этой высокоупорядоченной структуры. Такая структура демонстрирует дискретную трансляционную симметрию . Чтобы моделировать и изучать такую периодическую систему, нужна математическая «ручка» для описания симметрии и, следовательно, для выводов о свойствах материала, вытекающих из этой симметрии. Ячейка Вигнера–Зейтца является средством для достижения этого.
Ячейка Вигнера–Зейтца является примером примитивной ячейки , которая является элементарной ячейкой, содержащей ровно одну точку решетки. Для любой заданной решетки существует бесконечное число возможных примитивных ячеек. Однако для любой заданной решетки существует только одна ячейка Вигнера–Зейтца. Это геометрическое место точек в пространстве, которые находятся ближе к этой точке решетки, чем к любой другой точке решетки.
Ячейка Вигнера–Зейтца, как и любая примитивная ячейка, является фундаментальной областью для дискретной трансляционной симметрии решетки. Примитивная ячейка обратной решетки в импульсном пространстве называется зоной Бриллюэна .
Концепция разложения Вороного была исследована Петером Густавом Леженом Дирихле , что привело к названию область Дирихле . Дальнейшие вклады были сделаны Евграфом Федоровым ( параллелоэдр Федорова ), Георгием Вороным ( многогранник Вороного ), [1] [2] и Полом Ниггли ( Wirkungsbereich ). [3]
Применение к физике конденсированного состояния впервые было предложено Юджином Вигнером и Фредериком Зейтцем в статье 1933 года, где оно использовалось для решения уравнения Шредингера для свободных электронов в элементарном натрии . [4] Они аппроксимировали форму ячейки Вигнера-Зейтца в натрии, которая представляет собой усеченный октаэдр, как сферу равного объема и решили уравнение Шредингера точно, используя периодические граничные условия , которые требуют на поверхности сферы. Аналогичный расчет, который также учитывал несферическую природу ячейки Вигнера-Зейтца, был выполнен позже Джоном С. Слейтером . [5]
Существует только пять топологически различных многогранников, которые заполняют трехмерное пространство , ℝ 3 . Они называются параллелоэдрами . Они являются предметом математического интереса, например, в более высоких измерениях. [6] Эти пять параллелоэдров могут быть использованы для классификации трехмерных решеток с использованием концепции проективной плоскости, как предложили Джон Хортон Конвей и Нил Слоан . [7] Однако, в то время как топологическая классификация рассматривает любое аффинное преобразование как приводящее к идентичному классу, более конкретная классификация приводит к 24 различным классам многогранников Вороного с параллельными ребрами, которые заполняют пространство. [3] Например, прямоугольный кубоид , правильная квадратная призма и куб принадлежат к одному и тому же топологическому классу, но отличаются разными соотношениями своих сторон. Эта классификация 24 типов многогранников Вороного для решеток Браве была впервые изложена Борисом Делоне . [8]
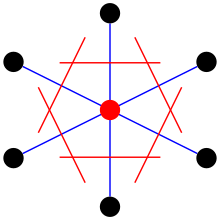
Ячейка Вигнера-Зейтца вокруг точки решетки определяется как геометрическое место точек в пространстве, которые находятся ближе к этой точке решетки, чем к любой другой точке решетки. [9]
Можно математически показать, что ячейка Вигнера-Зейтца является примитивной ячейкой . Это означает, что ячейка охватывает все прямое пространство, не оставляя никаких зазоров или отверстий, свойство, известное как тесселяция .
Общая математическая концепция, воплощенная в ячейке Вигнера-Зейтца, чаще называется ячейкой Вороного , а разбиение плоскости на эти ячейки для заданного набора точечных участков известно как диаграмма Вороного .

Ячейку можно выбрать, сначала выбрав точку решетки . После выбора точки линии рисуются ко всем близлежащим точкам решетки. В средней точке каждой линии рисуется еще одна линия, перпендикулярная каждой из первых линий. Наименьшая область, заключенная таким образом, называется примитивной ячейкой Вигнера–Зейтца .
Для трехмерной решетки шаги аналогичны, но на шаге 2 вместо рисования перпендикулярных линий рисуются перпендикулярные плоскости в средней точке линий между узлами решетки.
Как и в случае всех примитивных ячеек, вся область или пространство внутри решетки могут быть заполнены ячейками Вигнера–Зейтца, и не будет никаких пробелов.
Соседние точки решетки непрерывно проверяются до тех пор, пока площадь или объем, заключенные в них, не станут правильной площадью или объемом для примитивной ячейки . В качестве альтернативы, если базисные векторы решетки уменьшаются с помощью уменьшения решетки, необходимо использовать только заданное количество точек решетки. [10] В двух измерениях необходимо использовать только те точки решетки, которые составляют 4 элементарные ячейки, которые имеют общую вершину с началом координат. В трех измерениях необходимо использовать только те точки решетки, которые составляют 8 элементарных ячеек, которые имеют общую вершину с началом координат.
Для составных решеток (кристаллов, имеющих более одного вектора в своем базисе ) каждая отдельная точка решетки представляет собой несколько атомов. Мы можем разбить каждую ячейку Вигнера-Зейтца на подъячейки путем дальнейшего разложения Вороного в соответствии с ближайшим атомом, а не ближайшей точкой решетки. [12] Например, структура кристалла алмаза содержит двухатомный базис. В алмазе атомы углерода имеют тетраэдрическую связь sp 3 , но поскольку тетраэдры не заполняют пространство , разложение Вороного структуры кристалла алмаза на самом деле представляет собой триакисоусеченные тетраэдрические соты . [13] Другим примером является применение разложения Вороного к атомам в фазах A15 , что образует полиэдральное приближение структуры Уэйра-Фелана .
Ячейка Вигнера–Зейтца всегда имеет ту же точечную симметрию, что и лежащая в основе решетка Браве . [9] Например, куб , усеченный октаэдр и ромбический додекаэдр имеют точечную симметрию O h , поскольку соответствующие решетки Браве, используемые для их создания, принадлежат к кубической решеточной системе , которая имеет точечную симметрию O h .
На практике ячейка Вигнера-Зейтца сама по себе редко используется в качестве описания прямого пространства , где вместо этого обычно используются обычные элементарные ячейки . Однако то же самое разложение чрезвычайно важно при применении к обратному пространству . Ячейка Вигнера-Зейтца в обратном пространстве называется зоной Бриллюэна , которая содержит информацию о том, будет ли материал проводником , полупроводником или изолятором .