Принцип Франка–Кондона

Правило квантовой химии относительно вибронных переходов

Рисунок 1. Диаграмма энергии принципа Франка-Кондона. Поскольку электронные переходы очень быстры по сравнению с ядерными движениями, колебательные состояния, в которые и из которых происходит поглощение и испускание, соответствуют минимальному изменению ядерных координат. В результате и поглощение, и испускание создают молекулы в колебательно- возбужденных состояниях . Показаны потенциальные ямы, благоприятствующие переходам с изменениями ν .

Принцип Франка-Кондона описывает интенсивности вибронных переходов, или поглощения или испускания фотона. Он гласит, что когда молекула претерпевает электронный переход, такой как ионизация, ядерная конфигурация молекулы не претерпевает существенных изменений. ^[1]

Обзор

Рисунок 2. Схематическое изображение спектров поглощения и флуоресценции, соответствующих энергетической диаграмме на рисунке 1. Симметрия обусловлена ​​одинаковой формой потенциальных ям основного и возбужденного состояний. Узкие линии обычно можно наблюдать только в спектрах разбавленных газов. Более темные кривые представляют неоднородное уширение тех же переходов, которые происходят в жидкостях и твердых телах. Электронные переходы между низшими колебательными уровнями электронных состояний (переход 0–0) имеют одинаковую энергию как в поглощении, так и в флуоресценции.

Рисунок 3. Полуклассическая маятниковая аналогия принципа Франка-Кондона. Вибронные переходы разрешены в классических точках поворота, поскольку и импульс, и ядерные координаты соответствуют на двух представленных энергетических уровнях. На этой иллюстрации предпочтительными являются колебательные переходы 0-2.

Принцип Франка–Кондона имеет хорошо обоснованную полуклассическую интерпретацию, основанную на оригинальном вкладе Джеймса Франка . ^[2] Электронные переходы относительно мгновенны по сравнению с временной шкалой ядерных движений, поэтому, если молекула должна перейти на новый колебательный уровень во время электронного перехода, этот новый колебательный уровень должен быть мгновенно совместим с ядерными положениями и импульсами колебательного уровня молекулы в исходном электронном состоянии. В полуклассической картине колебаний (колебаний) простого гармонического осциллятора необходимые условия могут возникать в точках поворота, где импульс равен нулю.

Классически принцип Франка-Кондона является приближением, что электронный переход, скорее всего, произойдет без изменения положений ядер в молекулярной сущности и ее окружении. Результирующее состояние называется состоянием Франка-Кондона, а вовлеченный переход — вертикальным переходом. Квантово-механическая формулировка этого принципа заключается в том, что интенсивность вибронного перехода пропорциональна квадрату интеграла перекрытия между колебательными волновыми функциями двух состояний, которые вовлечены в переход.

—  Сборник химических терминов ИЮПАК , 2-е издание (1997)

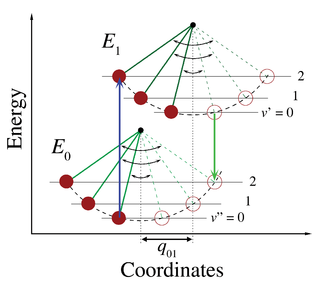
В квантово-механической картине колебательные уровни и колебательные волновые функции являются уровнями квантовых гармонических осцилляторов или более сложных приближений к потенциальной энергии молекул, таких как потенциал Морзе . Рисунок 1 иллюстрирует принцип Франка-Кондона для вибронных переходов в молекуле с функциями потенциальной энергии, подобными функциям Морзе, как в основном, так и в возбужденном электронном состоянии. В низкотемпературном приближении молекула начинает с колебательного уровня v = 0 основного электронного состояния и, поглощая фотон необходимой энергии, переходит в возбужденное электронное состояние. Электронная конфигурация нового состояния может привести к сдвигу положения равновесия ядер, составляющих молекулу. На рисунке 3 этот сдвиг ядерных координат между основным и первым возбужденным состоянием обозначен как q ₀₁ . В простейшем случае двухатомной молекулы ось ядерных координат относится к межъядерному разделению. Вибронный переход обозначен вертикальной стрелкой из-за предположения о постоянстве ядерных координат во время перехода. Вероятность того, что молекула может оказаться на каком-либо конкретном колебательном уровне, пропорциональна квадрату (вертикального) перекрытия колебательных волновых функций исходного и конечного состояний (см. раздел «Квантово-механическая формулировка» ниже). В электронно-возбужденном состоянии молекулы быстро релаксируют до самого низкого колебательного уровня самого низкого электронного возбужденного состояния ( правило Каши ), а оттуда могут распасться до основного электронного состояния посредством испускания фотона. Принцип Франка–Кондона применяется в равной степени к поглощению и флуоресценции .

Применимость принципа Франка-Кондона как в поглощении, так и в флуоресценции, наряду с правилом Каши приводит к приблизительной зеркальной симметрии, показанной на рисунке 2. Колебательная структура молекул в холодном разреженном газе наиболее отчетливо видна из-за отсутствия неоднородного уширения отдельных переходов. Вибронные переходы изображены на рисунке 2 как узкие, равноотстоящие друг от друга лоренцевы линии. Равное расстояние между колебательными уровнями имеет место только для параболического потенциала простых гармонических осцилляторов, в более реалистичных потенциалах, таких как те, что показаны на рисунке 1, энергетическое расстояние уменьшается с увеличением колебательной энергии. Электронные переходы в и из самых низких колебательных состояний часто называют переходами 0–0 (ноль ноль) и имеют одинаковую энергию как в поглощении, так и в флуоресценции.

Развитие принципа

В докладе, опубликованном в 1926 году в Transactions of the Faraday Society , Джеймс Франк был обеспокоен механизмами химических реакций, вызванных фотонами. Предполагаемым механизмом было возбуждение молекулы фотоном, за которым следовало столкновение с другой молекулой в течение короткого периода возбуждения. Вопрос заключался в том, возможно ли, чтобы молекула распалась на фотопродукты за один шаг, поглощение фотона, и без столкновения. Для того чтобы молекула распалась, она должна получить от фотона колебательную энергию, превышающую энергию диссоциации, то есть энергию для разрыва химической связи. Однако, как было известно в то время, молекулы будут поглощать только энергию, соответствующую разрешенным квантовым переходам, и нет колебательных уровней выше уровня энергии диссоциации потенциальной ямы . Поглощение высокоэнергетического фотона приводит к переходу в более высокое электронное состояние вместо диссоциации. Исследуя, сколько колебательной энергии может приобрести молекула, когда она возбуждается до более высокого электронного уровня, и может ли эта колебательная энергия быть достаточной для немедленного разрыва молекулы, он нарисовал три диаграммы, представляющие возможные изменения энергии связи между самым низким электронным состоянием и более высокими электронными состояниями.

Диаграмма I. показывает сильное ослабление связи при переходе из нормального состояния n в возбужденные состояния a и a ' . Здесь мы имеем D > D' и D' > D". В то же время положение равновесия ядер смещается с возбуждением к большим значениям r . Если мы перейдем от положения равновесия (минимум потенциальной энергии) кривой n вертикально [ выделено мной] вверх к кривым a на Диаграмме I. частицы будут иметь потенциальную энергию больше D' и разлетятся. В этом случае мы имеем очень большое изменение энергии колебаний при возбуждении светом...

—  Джеймс Франк, 1926 г.

Джеймс Франк осознал, что изменения в колебательных уровнях могут быть следствием мгновенного характера возбуждения более высоких электронных энергетических уровней и нового положения равновесия для потенциала ядерного взаимодействия. Эдвард Кондон распространил это понимание за пределы фотореакций в статье Physical Review 1926 года под названием «Теория распределения интенсивности в полосовых системах». ^[3] Здесь он формулирует полуклассическую формулировку способом, весьма похожим на ее современную форму. Первая совместная ссылка на Франка и Кондона в отношении нового принципа появляется в том же выпуске Physical Review 1926 года в статье о полосовой структуре оксида углерода, написанной Рэймондом Бирджем .

Рисунок 5. Рисунок 1 в первой публикации Эдварда Кондона о том, что сейчас называется принципом Франка–Кондона [Кондон 1926]. Кондон решил наложить потенциальные кривые, чтобы проиллюстрировать метод оценки колебательных переходов.

Квантово-механическая формулировка

Рассмотрим электрический дипольный переход из начального колебательного состояния ( υ ) основного электронного уровня ( ε ), в некоторое колебательное состояние ( υ ′) возбужденного электронного состояния ( ε ′), (см. обозначение скобок ). Молекулярный дипольный оператор μ определяется зарядом (− e ) и местоположением ( r _i ) электронов , а также зарядами (+ Z _j e ) и местоположением ( R _j ) ядер : ${\displaystyle |\epsilon v\rangle }$ ${\displaystyle |\epsilon 'v'\rangle }$

${\displaystyle {\boldsymbol {\mu }}={\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N}=-e\sum \limits _{i}{\boldsymbol {r}}_{i}+e\sum \limits _{j}Z_{j}{\boldsymbol {R}}_{j}.}$

Амплитуда вероятности P для перехода между этими двумя состояниями определяется выражением

${\displaystyle P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle =\int {\psi '^{*}}{\boldsymbol {\mu }}\psi \,d\tau ,}$

где и — соответственно общие волновые функции начального и конечного состояния. Общие волновые функции являются произведением отдельных колебательных (зависящих от пространственных координат ядер) и электронных пространственных и спиновых волновых функций: ${\displaystyle \psi }$ ${\displaystyle \psi '}$

${\displaystyle \psi =\psi _{e}\psi _{v}\psi _{s}.}$

Это разделение электронных и колебательных волновых функций является выражением приближения Борна–Оппенгеймера и является фундаментальным предположением принципа Франка–Кондона. Объединение этих уравнений приводит к выражению для амплитуды вероятности в терминах отдельных вкладов электронного пространства, спина и колебательного взаимодействия:

${\displaystyle P=\left\langle \psi _{e}'\psi _{v}'\psi _{s}'\right|{\boldsymbol {\mu }}\left|\psi _{e}\psi _{v}\psi _{s}\right\rangle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}({\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N})\psi _{e}\psi _{v}\psi _{s}\,d\tau }$

${\displaystyle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\psi _{s}\,d\tau +\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{N}\psi _{e}\psi _{v}\psi _{s}\,d\tau }$

${\displaystyle =\underbrace {\int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}} _{\displaystyle {{\text{Franck–Condon}} \atop {\text{factor}}}}\underbrace {\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}} _{\displaystyle {{\text{orbital}} \atop {\text{selection rule}}}}\underbrace {\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}} _{\displaystyle {{\text{spin}} \atop {\text{selection rule}}}}+\underbrace {\int \psi _{e}'^{*}\psi _{e}\,d\tau _{e}} _{\displaystyle 0}\int \psi _{v}'^{*}{\boldsymbol {\mu }}_{N}\psi _{v}\,d\tau _{v}\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}.}$

Независимая от спина часть исходного интеграла здесь аппроксимируется как произведение двух интегралов:

${\displaystyle \iint \psi _{v}'^{*}\psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\,d\tau _{e}d\tau _{n}\approx \int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}.}$

Эта факторизация была бы точной, если бы интеграл по пространственным координатам электронов не зависел от ядерных координат. Однако в приближении Борна–Оппенгеймера и зависят (параметрически) от ядерных координат, так что интеграл (так называемая переходная дипольная поверхность ) является функцией ядерных координат. Поскольку зависимость обычно довольно гладкая, ею пренебрегают (т. е. часто допускается предположение о независимости переходной дипольной поверхности от ядерных координат, называемое приближением Кондона ). ${\displaystyle \int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}}$ ${\displaystyle \psi _{e}}$ ${\displaystyle \psi '_{e}}$

Первый интеграл после знака плюс равен нулю, поскольку электронные волновые функции различных состояний ортогональны. Оставшийся интеграл является произведением трех интегралов. Первый интеграл является интегралом колебательного перекрытия, также называемым фактором Франка–Кондона . Оставшиеся два интеграла, вносящие вклад в амплитуду вероятности, определяют электронные пространственные и спиновые правила отбора.

Принцип Франка–Кондона — это утверждение о разрешенных колебательных переходах между двумя различными электронными состояниями; другие квантово-механические правила отбора могут снизить вероятность перехода или вообще запретить его. Вращательные правила отбора были проигнорированы в приведенном выше выводе. Вращательные вклады можно наблюдать в спектрах газов, но они сильно подавлены в жидкостях и твердых телах.

Должно быть ясно, что квантово-механическая формулировка принципа Франка-Кондона является результатом ряда приближений, в основном предположения об электрическом дипольном переходе и приближения Борна-Оппенгеймера. Более слабые магнитные дипольные и электрические квадрупольные электронные переходы вместе с неполной справедливостью факторизации полной волновой функции на ядерные, электронные пространственные и спиновые волновые функции означают, что правила отбора, включая фактор Франка-Кондона, не соблюдаются строго. Для любого заданного перехода значение P определяется всеми правилами отбора, однако наибольший вклад вносит спиновый отбор, за которым следуют электронные правила отбора. Фактор Франка-Кондона лишь слабо модулирует интенсивность переходов, т. е. он вносит вклад с множителем порядка 1 в интенсивность полос, порядок величины которых определяется другими правилами отбора. В таблице ниже приведен диапазон коэффициентов экстинкции для возможных комбинаций разрешенных и запрещенных спиновых и орбитальных правил отбора.

Метафоры Франка–Кондона в спектроскопии

Принцип Франка-Кондона в его канонической форме применяется только к изменениям вибрационных уровней молекулы в ходе изменения электронных уровней либо путем поглощения, либо путем испускания фотона. Физическая интуиция этого принципа основана на идее, что ядерные координаты атомов, составляющих молекулу, не успевают измениться в течение очень короткого промежутка времени, необходимого для электронного перехода. Однако эта физическая интуиция может быть, и действительно, обычно распространяется на взаимодействия между поглощающими или испускающими свет молекулами ( хромофорами ) и их окружением. Метафоры Франка-Кондона уместны, поскольку молекулы часто сильно взаимодействуют с окружающими молекулами, особенно в жидкостях и твердых телах, и эти взаимодействия изменяют ядерные координаты хромофора способами, очень похожими на молекулярные колебания, рассматриваемые принципом Франка-Кондона.

Рисунок 6. Энергетическая диаграмма электронного перехода с фононной связью вдоль конфигурационной координаты q _i , нормальной моды решетки. Стрелки, направленные вверх, представляют поглощение без фононов и с тремя фононами. Стрелки, направленные вниз, представляют симметричный процесс при излучении.

Принцип Франка–Кондона для фононов

Ближайшая аналогия Франка–Кондона обусловлена ​​взаимодействием фононов ( квантов колебаний решетки ) с электронными переходами хромофоров, внедренных в решетку в качестве примесей. В этой ситуации переходы на более высокие электронные уровни могут иметь место, когда энергия фотона соответствует чисто электронной энергии перехода или чисто электронной энергии перехода плюс энергия одного или нескольких фононов решетки. В низкотемпературном приближении излучение происходит с нулевого фононного уровня возбужденного состояния на нулевой фононный уровень основного состояния или на более высокие фононные уровни основного состояния. Так же, как в принципе Франка–Кондона, вероятность переходов с участием фононов определяется перекрытием волновых функций фононов на начальном и конечном уровнях энергии. Для принципа Франка–Кондона, примененного к фононным переходам, обозначение горизонтальной оси рисунка 1 заменяется на рисунке 6 на конфигурационную координату для нормальной моды . Потенциальная энергия решеточной моды на рисунке 6 представлена ​​как энергия гармонического осциллятора, а расстояние между фононными уровнями ( ) определяется параметрами решетки. Поскольку энергия отдельных фононов обычно довольно мала, переходы с нулевым или малым числом фононов можно наблюдать только при температурах ниже примерно 40 кельвинов . ${\displaystyle q_{i}}$ ${\displaystyle \hbar \Omega _{i}}$

Более подробную информацию и ссылки см . в разделах Линия нулевого фонона и Боковая фононная полоса .

Принцип Франка–Кондона в сольватации

Рисунок 7. Энергетическая диаграмма, иллюстрирующая принцип Франка–Кондона, применяемый к сольватации хромофоров. Параболические потенциальные кривые символизируют энергию взаимодействия между хромофорами и растворителем. Гауссовы кривые представляют распределение этой энергии взаимодействия.

Рассмотрения Франка–Кондона можно также применить к электронным переходам хромофоров, растворенных в жидкостях. При таком использовании метафоры Франка–Кондона колебательные уровни хромофоров, а также взаимодействия хромофоров с фононами в жидкости продолжают вносить вклад в структуру спектров поглощения и испускания, но эти эффекты рассматриваются отдельно и независимо.

Рассмотрим хромофоры, окруженные молекулами растворителя . Эти окружающие молекулы могут взаимодействовать с хромофорами, особенно если молекулы растворителя полярны . Эта ассоциация между растворителем и растворенным веществом называется сольватацией и является стабилизирующим взаимодействием, то есть молекулы растворителя могут двигаться и вращаться до тех пор, пока энергия взаимодействия не будет минимизирована. Само взаимодействие включает электростатические и силы Ван-дер-Ваальса , а также может включать водородные связи . Принципы Франка-Кондона могут применяться, когда взаимодействия между хромофором и окружающими молекулами растворителя различны в основном и возбужденном электронном состоянии. Это изменение во взаимодействии может возникать, например, из-за различных дипольных моментов в этих двух состояниях. Если хромофор начинает находиться в своем основном состоянии и близок к равновесию с окружающими молекулами растворителя, а затем поглощает фотон, который переводит его в возбужденное состояние, его взаимодействие с растворителем будет далеким от равновесия в возбужденном состоянии. Этот эффект аналогичен исходному принципу Франка–Кондона: электронный переход очень быстр по сравнению с движением ядер — перестройкой молекул растворителя в случае сольватации. Теперь мы говорим о вертикальном переходе, но теперь горизонтальная координата — это пространство взаимодействия растворителя и растворенного вещества. Эта ось координат часто обозначается как «координата сольватации» и представляет, несколько абстрактно, все соответствующие измерения движения всех взаимодействующих молекул растворителя.

В исходном принципе Франка-Кондона после электронного перехода молекулы, которые оказываются в более высоких колебательных состояниях, немедленно начинают релаксировать в самое низкое колебательное состояние. В случае сольватации молекулы растворителя немедленно попытаются перестроиться, чтобы минимизировать энергию взаимодействия. Скорость релаксации растворителя зависит от вязкости растворителя . Если предположить, что время релаксации растворителя коротко по сравнению со временем жизни электронного возбужденного состояния, то эмиссия будет происходить из самого низкого энергетического состояния растворителя возбужденного электронного состояния. Для низкомолекулярных растворителей, таких как вода или метанол , при температуре окружающей среды время релаксации растворителя составляет порядка нескольких десятков пикосекунд , тогда как время жизни возбужденного состояния хромофора составляет от нескольких пикосекунд до нескольких наносекунд . Сразу после перехода в основное электронное состояние молекулы растворителя также должны перестроиться, чтобы приспособиться к новой электронной конфигурации хромофора. Рисунок 7 иллюстрирует принцип Франка-Кондона, примененный к сольватации. При освещении раствора светом, соответствующим энергии электронного перехода, некоторые хромофоры перейдут в возбужденное состояние. Внутри этой группы хромофоров будет статистическое распределение энергий взаимодействия растворителя с хромофором, представленное на рисунке функцией распределения Гаусса . Взаимодействие растворителя с хромофором изображено как параболический потенциал в обоих электронных состояниях. Поскольку электронный переход по существу мгновенный на временной шкале движения растворителя (вертикальная стрелка), совокупность хромофоров возбужденного состояния сразу же оказывается далекой от равновесия. Перераспределение молекул растворителя в соответствии с новой кривой потенциальной энергии представлено изогнутыми стрелками на рисунке 7. Обратите внимание, что в то время как электронные переходы квантуются, энергия взаимодействия хромофора с растворителем рассматривается как классический континуум из-за большого числа вовлеченных молекул. Хотя эмиссия изображена как происходящая из минимума потенциала взаимодействия хромофора и растворителя в возбужденном состоянии, значительная эмиссия может иметь место до достижения равновесия, когда вязкость растворителя высока или время жизни возбужденного состояния короткое. Разница энергий между поглощенными и испущенными фотонами, изображенная на рисунке 7, является сольватационным вкладом в сдвиг Стокса .

Смотрите также

• Приближение Борна-Оппенгеймера
• Молекулярный электронный переход
• Ультрафиолетово-видимая спектроскопия
• Квантовый гармонический осциллятор
• потенциал Морзе
• Вибронная муфта
• Линия с нулевым фононом и фононная боковая полоса
• Внезапное приближение

Ссылки

1. Ссылки 20изменение.
2. Франк, Дж. (1926). «Элементарные процессы фотохимических реакций». Труды Фарадейского общества . 21 : 536–542. doi :10.1039/tf9262100536.
3. Кондон, Эдвард (1926-12-01). "Теория распределения интенсивности в полосовых системах". Physical Review . 28 (6): 1182–1201. Bibcode : 1926PhRv...28.1182C. doi : 10.1103/PhysRev.28.1182.

Дальнейшее чтение

• Франк, Дж. (1926). «Элементарные процессы фотохимических реакций». Труды Фарадейского общества . 21 : 536–542. doi :10.1039/tf9262100536.Связь
• Кондон, Э. (1926). "Теория распределения интенсивности в полосовых системах (Аннотация заседания)". Physical Review . 27 (5): 640. Bibcode :1926PhRv...27..637.. doi :10.1103/PhysRev.27.637.
• Кондон, Э. (1926). «Теория распределения интенсивности в полосовых системах». Physical Review . 28 (6): 1182–1201. Bibcode : 1926PhRv...28.1182C. doi : 10.1103/PhysRev.28.1182.Ссылка Архивировано 28.12.2011 на Wayback Machine
• Кондон, Э. (1928). «Ядерные движения, связанные с электронными переходами в двухатомных молекулах». Physical Review . 32 (6): 858–872. Bibcode : 1928PhRv...32..858C. doi : 10.1103/PhysRev.32.858.Ссылка Архивировано 28.12.2011 на Wayback Machine
• Бирге, РТ (1926). «Полосные спектры оксида углерода». Physical Review . 28 (6): 1157–1181. Bibcode : 1926PhRv...28.1157B. doi : 10.1103/PhysRev.28.1157.Ссылка Архивировано 28.12.2011 на Wayback Machine
• Noyes, WA (1933). «Корреляция спектроскопии и фотохимии». Reviews of Modern Physics . 5 (4): 280–287. Bibcode : 1933RvMP....5..280N. doi : 10.1103/RevModPhys.5.280.Связь
• Кулидж, А. С., Джеймс, Х. М. и Презент, Р. Д. (1936). «Исследование принципа Франка–Кондона». Журнал химической физики . 4 (3): 193–211. Bibcode : 1936JChPh...4..193C. doi : 10.1063/1.1749818.{{cite journal}}: CS1 maint: multiple names: authors list (link)Связь
• Герцберг, Герхард (1971). Спектры и структуры простых свободных радикалов . Нью-Йорк: Довер . ISBN 0-486-65821-X.
• Харрис, Дэниел С.; Майкл Д. Бертолуччи (1978). Симметрия и спектроскопия . Нью-Йорк: Довер. ISBN 0-486-66144-X.
• Бернат, Питер Ф. (1995). Спектры атомов и молекул (Темы физической химии) . Оксфорд: Oxford University Press . ISBN 0-19-507598-6.
• Аткинс, П. В.; Р. С. Фридман (1999). Молекулярная квантовая механика . Оксфорд: Oxford University Press. ISBN 0-19-855947-X.

Внешние ссылки

• Рабинович Э.; Говинджи (1969). «Поглощение света и судьба энергии возбуждения: принцип Франка-Кондона». Науки о жизни в Университете Иллинойса в Урбане-Шампейне . Получено 18 мая 2024 г.