
В дискретной математике , а точнее в теории графов , граф — это структура, состоящая из набора объектов, в котором некоторые пары объектов в некотором смысле «связаны». Объекты представлены абстракциями, называемыми вершинами (также называемыми узлами или точками ), и каждая из связанных пар вершин называется ребром (также называемым ссылкой или линией ). [1] Обычно граф изображается в схематической форме в виде набора точек или кругов для вершин, соединенных линиями или кривыми для ребер.
Края могут быть направленными и ненаправленными. Например, если вершины представляют людей на вечеринке, и между двумя людьми, если они пожимают друг другу руки, есть ребро, то этот граф является неориентированным, поскольку любой человек A может пожать руку человеку B только в том случае, если B также пожимает руку A. Напротив, если ребро от человека A к человеку B означает, что A должен деньги B , тогда этот граф является направленным, поскольку задолженность по деньгам не обязательно является взаимной.
Графы — основной предмет, изучаемый теорией графов. Слово «график» впервые было использовано в этом смысле Дж. Дж. Сильвестром в 1878 году из-за прямой связи между математикой и химической структурой (то, что он назвал химико-графическим изображением). [2] [3]
Определения в теории графов различаются. Ниже приведены некоторые из наиболее основных способов определения графиков и связанных с ними математических структур .

Граф (иногда называемый неориентированным графом , чтобы отличить его от ориентированного графа, или простым графом , чтобы отличить его от мультиграфа ) [4] [5] представляет собой пару G = ( V , E ) , где V — множество, у которого элементы называются вершинами (единственное число: вершина), а E — набор неупорядоченных пар вершин, элементы которых называются ребрами (иногда ссылками или линиями ).
Вершины u и v ребра { u , v } называются конечными точками ребра . Говорят, что ребро соединяет u и v и инцидентно им . Вершина не может принадлежать ни одному ребру; в этом случае она не соединяется ни с одной другой вершиной и называется изолированной . Если ребро существует, вершины u и v называются смежными .
Мультиграф — это обобщение , позволяющее нескольким ребрам иметь одну и ту же пару конечных точек. В некоторых текстах мультиграфы называют просто графами. [6] [7]
Иногда графам разрешается содержать петли — ребра, соединяющие вершину с самой собой. Чтобы разрешить циклы, парам вершин в E должно быть разрешено иметь один и тот же узел дважды. Такие обобщенные графы называются графами с петлями или просто графами , если из контекста ясно, что петли разрешены.
Обычно множество вершин V считается конечным (что означает, что множество ребер E также конечно). Иногда рассматривают бесконечные графы , но обычно их рассматривают как особый вид бинарных отношений , поскольку большинство результатов о конечных графах либо не распространяются на бесконечный случай, либо требуют совсем иного доказательства.
Пустой граф — это граф, имеющий пустое множество вершин (и, следовательно, пустое множество ребер). Порядок графа — это его номер | В | вершин, обычно обозначаемых n . Размер графа — это его номер | Е | ребер, обычно обозначаемых m . Однако в некоторых контекстах, например для выражения вычислительной сложности алгоритмов, термин « размер» используется для обозначения величины | В | + | Е | (в противном случае непустой граф мог бы иметь размер 0). Степень или валентность вершины — это количество инцидентных ей ребер; для графов с циклами цикл учитывается дважды.
В графе порядка n максимальная степень каждой вершины равна n - 1 (или n + 1 , если циклы разрешены, поскольку цикл вносит 2 в степень), а максимальное количество ребер равно n ( n - 1). /2 (или n ( n + 1)/2, если циклы разрешены).
Ребра графа определяют симметричное отношение на вершинах, называемое отношением смежности . В частности, две вершины x и y являются смежными, если { x , y } является ребром. Граф полностью определяется своей матрицей смежности A , которая представляет собой квадратную матрицу размера n × n , где A ij определяет количество соединений от вершины i к вершине j . Для простого графа A ij равен либо 0, что указывает на разъединение, либо 1, что указывает на соединение; более того, A ii = 0, поскольку ребро в простом графе не может начинаться и заканчиваться в одной и той же вершине. Графы с циклами будут характеризоваться тем, что некоторые или все A ii равны положительному целому числу, а мультиграфы (с несколькими ребрами между вершинами) будут характеризоваться тем, что некоторые или все A ij равны положительному целому числу. Неориентированные графы будут иметь симметричную матрицу смежности (что означает A ij = A ji ).

Ориентированный граф или орграф — это граф, в котором ребра имеют ориентацию.
В одном ограниченном, но очень общепринятом смысле этого термина [8] ориентированный граф — это пара G = ( V , E ) , содержащая:
Во избежание двусмысленности объект такого типа можно назвать именно ориентированным простым графом .
В ребре ( x , y ) , направленном от x к y , вершины x и y называются концами ребра, x - хвостом ребра и y - головкой ребра . Говорят, что ребро соединяет x и y и инцидентно x и y . Вершина может существовать в графе и не принадлежать ребру. Ребро ( y , x ) называется перевернутым ребром ( x , y ) . Множественные ребра , недопустимые согласно приведенному выше определению, представляют собой два или более ребра с одинаковым хвостом и одной и той же головкой.
В более общем смысле термина, допускающего наличие кратных ребер, [8] ориентированный граф иногда определяется как упорядоченная тройка G = ( V , E , φ ) , содержащая:
Во избежание двусмысленности объект такого типа можно назвать именно ориентированным мультиграфом .
Петля — это ребро , которое соединяет вершину с самой собой. Ориентированные графы, определенные в двух определениях выше, не могут иметь петель, поскольку петля, соединяющая вершину с самой собой, является ребром (для ориентированного простого графа) или инцидентом (для ориентированного мультиграфа), которого нет в . Поэтому, чтобы разрешить циклы, определения должны быть расширены. Для ориентированных простых графов определение следует изменить на . Для ориентированных мультиграфов определение следует изменить на . Чтобы избежать двусмысленности, эти типы объектов можно назвать именно направленным простым графом, допускающим циклы , и ориентированным мультиграфом, допускающим циклы (или колчаном ) соответственно.
Ребра ориентированного простого графа, допускающие петли G, представляют собой однородное отношение С на вершинах графа G , называемое отношением смежности графа G. В частности, для каждого ребра ( x , y ) его конечные точки x и y считаются смежными друг с другом, что обозначается x ~ y .
Смешанный граф — это граф, в котором некоторые ребра могут быть направленными, а некоторые — ненаправленными. Это упорядоченная тройка G = ( V , E , A ) для смешанного простого графа и G = ( V , E , A , φ E , φ A ) для смешанного мультиграфа с V , E (неориентированные ребра), A (направленные ребра), φ E и φ A , определенные выше. Ориентированные и неориентированные графы являются особыми случаями.
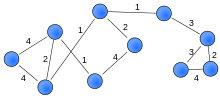
Взвешенный граф или сеть [ 9] [10] — это граф, в котором каждому ребру присвоено число (вес). [11] Такие веса могут отражать, например, стоимость, длину или мощность, в зависимости от решаемой проблемы. Такие графы возникают во многих контекстах, например, в задачах о кратчайшем пути, таких как задача коммивояжера .
Одно из определений ориентированного графа состоит в том, что это ориентированный граф, в котором не более одного из ( x , y ) и ( y , x ) может быть ребром графа. То есть это ориентированный граф, который можно сформировать как ориентацию неориентированного (простого) графа.
Некоторые авторы используют термин «ориентированный граф» для обозначения того же, что и «ориентированный граф». Некоторые авторы используют термин «ориентированный граф» для обозначения любой ориентации данного неориентированного графа или мультиграфа.
Правильный граф — это граф, в котором каждая вершина имеет одинаковое количество соседей, т. е. каждая вершина имеет одинаковую степень. Регулярный граф с вершинами степени k называется k -регулярным графом или регулярным графом степени k .

Полный граф — это граф, в котором каждая пара вершин соединена ребром. Полный граф содержит все возможные ребра.
Конечный граф — это граф, в котором множество вершин и множество ребер являются конечными множествами . В противном случае его называют бесконечным графом .
Чаще всего в теории графов подразумевается, что обсуждаемые графы конечны. Если графы бесконечны, это обычно специально оговаривается.
В неориентированном графе неупорядоченная пара вершин { x , y } называется связной , если путь ведет от x к y . В противном случае неупорядоченная пара называется несвязной .
Связный граф — это неориентированный граф, в котором каждая неупорядоченная пара вершин графа связна. В противном случае его называют несвязным графом .
В ориентированном графе упорядоченная пара вершин ( x , y ) называется сильно связной, если направленный путь ведет от x к y . В противном случае упорядоченная пара называется слабосвязной, если ненаправленный путь ведет от x к y после замены всех ее направленных ребер ненаправленными. В противном случае упорядоченная пара называется несвязной .
Сильно связный граф — это ориентированный граф, в котором каждая упорядоченная пара вершин графа сильно связна. В противном случае граф называется слабо связным, если каждая упорядоченная пара вершин графа слабо связна. В противном случае его называют несвязным графом .
Граф с k-вершиной связности или граф с k-связностью ребер — это граф, в котором не существует множества из k - 1 вершин (соответственно ребер), удаление которых разъединяет граф. Граф с k -связностью часто называют просто k-связным графом .
Двудольный граф — это простой граф, в котором множество вершин можно разделить на два множества, W и X , так что никакие две вершины в W не имеют общего ребра и никакие две вершины в X не имеют общего ребра. Альтернативно, это граф с хроматическим числом 2.
В полном двудольном графе множество вершин представляет собой объединение двух непересекающихся множеств, W и X , так что каждая вершина в W смежна с каждой вершиной в X , но внутри W или X нет ребер .
Граф путей или линейный граф порядка n ≥ 2 — это граф, в котором вершины могут быть перечислены в порядке v 1 , v 2 , …, v n так, что ребрами являются { v i , v i +1 } , где i = 1, 2, …, n − 1. Графы путей можно охарактеризовать как связные графы, в которых степень всех вершин, кроме двух, равна 2, а степень двух оставшихся вершин равна 1. Если граф путей встречается как подграф другого графа, это путь в этом графе.
Планарный граф — это граф, вершины и ребра которого можно нарисовать на плоскости так, что никакие два ребра не пересекаются.
Граф циклов или круговой граф порядка n ≥ 3 — это граф, в котором вершины могут быть перечислены в порядке v 1 , v 2 , …, v n так, что ребрами являются { v i , v i +1 } , где я знак равно 1, 2, …, n - 1, плюс ребро { v n , v 1 } . Графы циклов можно охарактеризовать как связные графы, в которых степень всех вершин равна 2. Если граф циклов встречается как подграф другого графа, он является циклом или схемой в этом графе.
Дерево — это неориентированный граф, в котором любые две вершины соединены ровно одним путем , или, что то же самое, связный ациклический неориентированный граф.
Лес — это неориентированный граф, в котором любые две вершины соединены не более чем одним путем, или, что то же самое , ациклический неориентированный граф или, что то же самое, непересекающееся объединение деревьев.
Полидерево (или ориентированное дерево , или ориентированное дерево , или односвязная сеть ) — это ориентированный ациклический граф (DAG) , базовым неориентированным графом которого является дерево.
Полилес (или направленный лес или ориентированный лес ) — это ориентированный ациклический граф , базовым неориентированным графом которого является лес.
Более продвинутые виды графиков:
Два ребра графа называются смежными , если они имеют общую вершину. Два ребра ориентированного графа называются последовательными , если голова первого является хвостом второго. Аналогично, две вершины называются смежными, если они имеют общее ребро ( последовательными , если первая вершина является хвостом, а вторая — головой ребра), и в этом случае говорят, что общее ребро соединяет две вершины. Ребро и вершина на этом ребре называются инцидентными .
Граф, имеющий только одну вершину и не имеющий ребер, называется тривиальным графом . Граф, имеющий только вершины и не имеющий ребер, называется графом без ребер . Граф без вершин и ребер иногда называют нулевым графом или пустым графом , но терминология непоследовательна, и не все математики допускают этот объект.
Обычно вершины графа по своей природе как элементы множества различимы. Этот вид графа можно назвать помеченным вершинами . Однако во многих вопросах лучше считать вершины неразличимыми. (Конечно, вершины еще можно различать по свойствам самого графа, например, по количеству инцидентных ребер.) Те же замечания применимы и к ребрам, поэтому графы с помеченными ребрами называются помеченными ребрами . Графы с метками, прикрепленными к ребрам или вершинам, обычно называются помеченными . Следовательно, графы, в которых вершины неразличимы, а ребра неразличимы, называются неразмеченными . (В литературе термин «размеченный» может применяться к другим видам разметки, помимо того, который служит только для различения различных вершин или ребер.)
Категория всех графов — это категория с запятой Set ↓ D, где D : Set → Set — это функтор, переводящий набор s в s × s .

Существует несколько операций, которые создают новые графы из исходных, которые можно разделить на следующие категории:
В гиперграфе ребро может соединять любое положительное количество вершин.
Неориентированный граф можно рассматривать как симплициальный комплекс , состоящий из 1- симплексов (ребер) и 0-симплексов (вершин). По сути, комплексы являются обобщением графов, поскольку они допускают симплексы более высокой размерности.
Каждый граф порождает матроид .
В теории моделей граф — это просто структура . Но в таком случае ограничений на количество ребер нет: это может быть любое кардинальное число , см. непрерывный граф .
В вычислительной биологии анализ степенных графов представляет степенные графы как альтернативное представление неориентированных графов.
В географических информационных системах геометрические сети тесно моделируются по образцу графов и заимствуют многие концепции из теории графов для выполнения пространственного анализа дорожных сетей или инженерных сетей.
Граф — это объект, состоящий из двух наборов, называемых набором вершин и набором ребер .
Взвешенный граф
— это граф, в котором каждому ребру e присвоено число w ( e ), называемое его весом .